|
|
|
发布时间: 2024-08-28 |
综合能源 |
|
|
|
收稿日期: 2024-03-06
中图法分类号: TK01+9
文献标识码: A
文章编号: 2096-8299(2024)04-0347-08
|
摘要
针对数据中心高能耗、高碳排放问题,提出了一种风险规避下面向建筑的数据中心综合能源系统低碳规划模型。首先,根据运行特性,建立了数据中心的全生命周期碳排放模型。其次,为解决碳排放计算不精确和可再生能源不确定性带来的风险问题,提出了基于动态碳排放因子的减碳策略和可再生能源间歇性风险度量方法(RIRM),以总成本最低和风险最小为目标函数,对数据中心综合能源系统内设备容量进行最优配置。最后,通过算例仿真验证了所提方法的低碳性和经济性,并将RIRM与条件风险价值(CVaR)进行了比较分析。
关键词
数据中心综合能源系统; 风险规避; 减碳策略; 碳排放因子
Abstract
Aiming at the problem of high energy consumption and high carbon emissions in data centers, a low-carbon planning model for building-oriented integrated energy systems of data centers under risk avoidance is proposed. First, a full life cycle carbon emission model of the data center is established based on operational characteristics. Then, in order to overcome the risk issues of imprecise limitations of carbon emission calculations and indeterminacy of renewable energy, a carbon reduction strategy based on dynamic carbon emission factors and RIRM method are proposed, with the lowest total cost and the lowest risk as the objective function, and the data center integrated energy system is optimally configure the equipment capacity. Finally, the lowcarbon nature and economy of the proposed method were verified through numerical examples, and the proposed RIRM method is analyzed and compared with CVaR.
Key words
data center integrated energy system; risk avoidance; carbon reduction strategy; carbon emission factor
随着全球对气候变化和环境问题的日益关注,作为数字化社会的支撑,数据中心因其高能耗、高碳排放成为运营商关注的重大问题。同时,综合能源系统凭借其在新能源消纳、综合能效以及经济运行等方面的优势[1],成为数据中心降低能源成本和环境压力的有效方法。
目前,国内外学者主要从柔性工作负载调度、使用可再生能源以及优化数据中心供能结构3个方面对如何降低数据中心能耗展开研究。柔性工作负载调度的原理在于充分利用部分计算任务具有时间维度推迟和空间维度转移的运行特性[2]。这种特性使得数据中心能够在不同时间段和不同服务器之间动态地调度和重新分配计算任务,以优化资源利用和能源消耗。文献[3-4]研究了虚拟机放置(Virtual Machine Place,VMP)方法,将工作负载分布在尽可能少的物理机上,以提高服务器的资源利用率和虚拟机密度。文献[5-6]针对地理位置分散的互联数据中心,利用电价的时刻差异性和地理多样性来降低数据中心运营商的能源成本。文献[7]构建了一种考虑多类型资源的数据中心园区供电协调规划模型。文献[8]提出了一种多能系统与数据中心集成的能源站最优选型方法。针对互联的数据中心,文献[9]建立了一种可用于确定数据中心微电网类型和服务器型号的规划模型。文献[10]提出了一种将工作负载迁移到由可再生能源供电的数据中心的处理方法。
然而,新能源功率输出存在季节性偏差[11],其间歇性输出会导致能源供应波动增大,使得数据中心的能源采购成本面临更大的不确定性。这对于数据中心运营商来说,是一个风险[12]。目前研究主要采用条件风险价值(Condition Value at Risk,CVaR)方法来规避可再生能源不确定性带来的尾部风险[13]。文献[14]针对新能源与负荷不确定性带来的市场风险,使用CVaR将省内电力市场出清转化为计及风险的多目标优化问题。然而,可再生能源的间歇性特性经常出现在较短的时间内[15],使CVaR无法很好地捕捉到这种短期波动。此外,在“双碳”背景下,碳排放交易体系和碳税等市场机制的实施迫使企业购买排放配额或支付额外碳税,导致企业经济成本上升。对于数据中心这类能源消耗较大的企业,碳排放所带来的成本损失更加显著。因此,为了更好地评估数据中心投资者在碳税等市场机制下的责任,进而有针对性地制定减排策略和措施,有必要对全生命周期的碳排放进行核算。
针对上述问题,本文提出了动态减碳策略和可再生能源间歇性功率输出风险度量方法。首先,根据运行特性建立数据中心全生命周期碳排放模型,在单一经济标准下,将碳排放转换为成本计入数据中心综合能源系统规划模型。其次,引入风险度量方法,评估可再生能源不确定性带来的风险成本。然后,基于碳排放流理论,提出一种基于动态碳排放因子调度工作负载降低碳排放的方法。最后,通过不同情形下的案例对比,分析所提动态减碳策略和风险度量方法的经济性。
1 数据中心全生命周期碳排放模型
1.1 模型结构
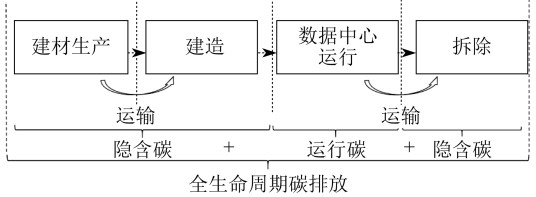
数据中心全生命周期碳排放模型可分为建筑材料(以下简称“建材”)生产、运输、建造、数据中心运行、拆除5个阶段,具体如图 1所示。本文假设服务器和设备的碳成本在购买时已经进行了交易,即不考虑服务器和能源设备的隐含碳排放。
1.2 生产阶段碳排放
生产阶段的碳排放主要来源于建材生产过程中所使用的电力和燃料。生产阶段碳排放量Epro,d的计算公式为
| $ E_{\mathrm{pro}, \mathrm{d}}=\sum\limits_{k=1}^K m_k\left(1+\delta_k\right) f_{\mathrm{mat}, k} $ | (1) |
式中:K——建材种类数量;
mk——第k种建材重量;
δk——第k种建材浪费率;
fmat,k——生产第k种建材的碳排放因子。
1.3 运输阶段碳排放
运输阶段是将建材和构件运送到施工现场的过程。这一过程的碳排放来源于运输车辆使用的燃料。运输阶段碳排放量Etra,d的计算公式为
| $ E_{\mathrm{tra}, \mathrm{d}}=\sum\limits_{k=1}^K m_k D_k f_{\mathrm{veh}, k} $ | (2) |
式中:Dk——第k种建材的运输距离;
fveh,k——运输第k种建材时,单位运输距离的碳排放因子。
1.4 建造阶段碳排放
数据中心施工过程中的碳排放主要来源于施工现场机械设备能耗产生的间接排放。建造阶段碳排放量Econ,d的计算公式为
| $ E_{\mathrm{con}, \mathrm{d}}=\sum\limits_{h=1}^H X_h f_{\mathrm{ene}, h} $ | (3) |
式中:H——建造施工现场能源类型数量;
Xh——施工阶段第h种能源消耗量;
fene,h——第h种能源的碳排放因子。
1.5 运行阶段碳排放
1.5.1 数据中心模型
到达数据中心的请求负载可以分为交互型负载和批处理负载两种。交互型负载在接收到请求时需要立即处理,而批处理负载允许在一定时间内延迟处理。在t时段,交互型和批处理负载请求的总数不能超过数据中心服务器最大处理容量限制,用公式表示为
| $ w_t=\sum\limits_p \alpha_{p, t}+\sum\limits_q \zeta_{q, t} $ | (4) |
| $ 0 \leqslant w_t \leqslant N_{\mathrm{dc}} v $ | (5) |
式中:wt——t时段到达数据中心的负载请求数;
αp,t——t时段第p个交互型负载接收到的请求数;
ζq,t——t时段第q个批处理负载接收到的请求数;
Ndc——数据中心服务器数量;
ν——服务器平均服务率。
本文采用电源使用效率(Power Usage Effectiveness,PUE)[16]来衡量能源使用效率,其定义为数据中心总功耗与服务器相关设备消耗电能的比值。
数据中心服务器消耗的电能计算公式为
| $ P_{\mathrm{cal}, t}=N_{\mathrm{dc}}\left(\lambda w_t+\mu\right) $ | (6) |
其中:
| $ \lambda=P_{\text {peak }}-P_{\text {idle }} $ | (7) |
| $ \mu=P_{\text {peak }}+\left(P_{\text {ue }}-1\right) P_{\text {idle }} $ | (8) |
式中:Pcal,t——t时段服务器消耗的电能;
Ppeak,Pidle——服务器在休眠和工作状态时消耗的电能;
Pue——电源使用效率。
假设非服务器设备消耗的电能全部用于服务器的冷却系统,则相关计算公式为
| $ Q_{h, t}=\left(P_{\mathrm{ue}}-1\right) P_{\mathrm{cal}, t} \eta_{\mathrm{col}} $ | (9) |
| $ Q_{h, t}=Q_{c, t} $ | (10) |
式中:Qh,t,Qc,t——数据中心废热量和制冷需求量;
ηcol——冷却系统的制冷系数。
在稳定状态下,计算过程中产生的废热量与制冷量相同。余热回收过程中消耗的电能公式为
| $ P_{\mathrm{col}, t}=\frac{Q_{c, t}}{\eta_{\mathrm{col}}} $ | (11) |
| $ P_{\mathrm{rec}, t}=\frac{Q_{h, t}}{\eta_{\mathrm{hp}}} $ | (12) |
式中:Pcol,t,Prec,t——t时段制冷功耗和余热回收功耗;
ηhp——热泵制热转化率。
1.5.2 供能模型
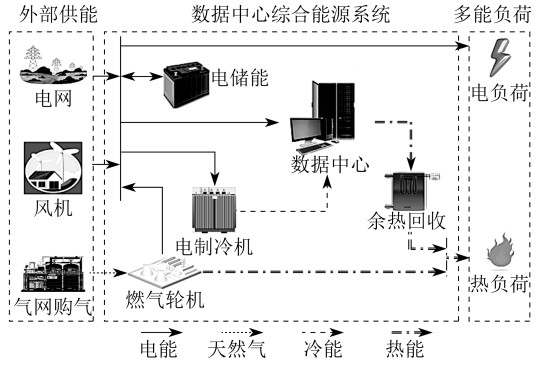
数据中心综合能源系统的供能结构如图 2所示。其中,数据中心由电网、风机、燃气轮机以及电储能设备供电,由电制冷机供冷。同时,数据中心的废热通过余热回收设备,将低品位热源转换为高品位热源,用于满足热负荷。
电储能设备的充放电功率公式及相关约束条件如下:
| $ E_{t+1}=E_t+\eta_{\mathrm{ch}} P_{\mathrm{ch}, t}-\eta_{\mathrm{dis}} P_{\mathrm{dis}, t} $ | (13) |
| $ E_t^{\min } \leqslant E_t \leqslant E_t^{\max } $ | (14) |
| $ Z_{\mathrm{ch}, t}, Z_{\mathrm{dis}, t} \in\{0,1\} $ | (15) |
| $ Z_{\mathrm{ch}, t}+Z_{\mathrm{dis}, t} \leqslant 1 $ | (16) |
| $ 0 \leqslant P_{\mathrm{ch}, t} \leqslant P_{\mathrm{ch}}^{\max } Z_{\mathrm{ch}, t} $ | (17) |
| $ 0 \leqslant P_{\mathrm{dis}, t} \leqslant P_{\mathrm{dis}}^{\max } Z_{\mathrm{dis}, t} $ | (18) |
式中:Et,Et+1——t时段和t+1时段的储能容量;
ηch,ηdis——电储能设备的充电效率和放电效率;
Pch,t,Pdis,t——t时段电储能设备的充电功率和放电功率;
Etmin,Etmax——t时段电储能设备最小、最大储能容量;
Zch,t,Zdis,t——t时段电储能设备的充、放电状态变量,均为二进制变量;
Pchmax,Pdismax——电储能设备的最大充电率和最大放电率。
数据中心所消耗的电力,无论是由电网还是发电设备提供,都会产生碳排放。因此,运行阶段碳排放量Eope,d的公式为
| $ E_{\mathrm{ope}, \mathrm{d}}=y \sum\limits_{t=1}^T P_{\mathrm{e}, t} f_{\mathrm{e}, t} $ | (19) |
| $ P_{\mathrm{e}, t}=P_{\mathrm{cal}, t}+P_{\mathrm{col}, t}+P_{\mathrm{rec}, t} $ | (20) |
式中:T——时间总长度;
y——全生命周期年限;
Pe,t——t时段数据中心运行阶段能耗;
fe,t——t时段电能对应的碳排放因子。
1.6 拆除阶段碳排放
建筑拆除阶段需要消耗大量的能源,产生的碳排放量Edem,d的公式为
| $ E_{\mathrm{dem}, \mathrm{d}}=\sum\limits_{h=1}^H u_h f_{\mathrm{ene}, h} $ | (21) |
式中:uh——建筑拆除阶段第h种能源的使用量。
综上,可以得到数据中心全生命周期的碳排放量Etotal,d的计算公式为
| $ E_{\text {total, } \mathrm{d}}=E_{\mathrm{pro}, \mathrm{d}}+E_{\text {tra, } \mathrm{d}}+E_{\mathrm{con}, \mathrm{d}}+E_{\mathrm{ope}, \mathrm{d}}+E_{\mathrm{dem}, \mathrm{d}} $ | (22) |
2 动态减碳策略
2.1 动态碳排放因子
碳排放一般根据能源消耗和能源碳排放因子计算,其中能源碳排放因子为平均碳排放因子,主要代表区域全年每千瓦时电力的平均碳含量。由于新能源电力比例和分布式清洁能源装机容量不断增加,不同时期不同地区碳排放因子的差异越来越明显,导致碳排放核算方法的时间和空间分辨率均有缺陷,因此需要一种能够反映碳排放因子时空差异的碳排放核算方法。
电力系统碳排放流理论通过给每条支路潮流加上碳排放标签,实现电力碳排放的责任分担[17]。该理论能够根据源侧发电量和线路潮流信息,将源侧发电的碳排放实时分配到电网侧和负荷侧。基于这一理论,可以得到电网的动态碳排放因子模型,公式为
| $ e_n=\frac{\sum\limits_{l \in N^{+}} P_l \alpha_l}{\sum\limits_{l \in N^{+}} P_l} $ | (23) |
式中:en——电网节点n的节点碳势;
l——支路编号;
Pl——支路l上的有功潮流;
N+——有功潮流流入电网节点n的支路集合;
αl——支路l的碳流密度。
2.2 基于碳排放因子的减碳策略
如果在碳排放因子值较低时分配较多的计算任务,在碳排放因子值较高时安排较少的工作负载,就可以减少数据中心能源消耗,进而减少运行阶段的碳排放。
使用函数G(×) 重新表示数据中心的能耗,每个时刻调度的批处理工作负载量表示为△wb,t,则与低碳控制方法相关的约束条件如下:
| $ w_t \leqslant N_{\mathrm{dc}} v $ | (24) |
| $ -\gamma P_{\mathrm{cal}, t} \leqslant G\left(\Delta w_{\mathrm{b}, t}\right) \leqslant \gamma P_{\mathrm{cal}, t} $ | (25) |
| $ \sum\limits_{t=1}^T G\left(\Delta w_{\mathrm{b}, t}\right)=0 $ | (26) |
| $ \max \left(\Delta w_{\mathrm{b}, t}\right) \leqslant D $ | (27) |
式中:γ——工作负载调度系数;
D——最大允许完成时间。
式(24)限定了工作负载请求数不得超过数据中心服务器总容量。式(25)限定了数据中心在t时段允许调度的工作请求数量。式(26)规定了调度前后处理的工作请求数量保持不变。为了保证数据中心的服务质量,最大允许完成时间限制由式(27)表示。
3 计及风险的低碳规划模型
3.1 预期成本函数
3.1.1 目标函数
预期成本函数Ctotal由投资成本Cinv、购能成本Cpur,s和碳排放成本Ccar,s组成,目标函数公式为
| $ C_{\text {total }}=\min\limits_{X_i, X_j, P_{z, t}}\left[C_{\mathrm{inv}}+\sum\limits_{s=1}^s p_s\left(C_{\mathrm{pur}, s}+C_{\mathrm{car}, s}\right)\right] $ | (28) |
| $ C_{\mathrm{inv}}=\frac{r(1+r)^y}{(1+r)^y-1}\left(\sum\limits_i X_i C_{\mathrm{m}, i}+\sum\limits_j X_j C_{\mathrm{m}, j}\right) $ | (29) |
| $ C_{\mathrm{pur}, s}=\sum\limits_{s=1}^S \sum\limits_{t=1}^T\left(P_{\mathrm{grid}, s, t} o_{\mathrm{e}, s, t}+P_{\mathrm{gas}, s, t} o_{\mathrm{g}, s, t}\right) $ | (30) |
| $ C_{\mathrm{car}, \mathrm{s}}=c_t\left(E_{\text {total, } \mathrm{d}}-E_{\text {quota }}\right) $ | (31) |
式中:Xi,Xj——设备i和j的规划容量;
Pz,t——t时段z类能源系统的功率;
S——场景总数;
ps——场景s出现的概率;
r——年贴现率;
Cm,i,Cm,j——设备i和j的投资成本;
Pgrid,s,t——场景s下t时段电能采购量;
oe,s,t——场景s下t时段的实时电价;
Pgas,s,t——场景s下t时段天然气采购量;
og,s,t——场景s下t时段的实时气价;
ct——碳税;
Equota——碳配额。
3.1.2 约束条件
各设备模型的约束条件如下:
i ∈ {燃气轮机},j ∈ {余热回收装置,电制冷机},
| $ z \in\{\text { 电网, 天然气, 电储能 }\} $ | (32) |
| $ 0 \leqslant X_i \leqslant X_i^{\max } $ | (33) |
| $ 0 \leqslant X_j \leqslant X_j^{\max } $ | (34) |
| $ P_i^{\min } \leqslant P_i \leqslant P_i^{\max } $ | (35) |
| $ P_{\mathrm{gt}, \mathrm{h}, s, t}+Q_{\mathrm{h}, s, t} \geqslant Q_{\text {load }, s, t} $ | (36) |
| $ \begin{array}{r} P_{\mathrm{grid}, s, t}+P_{\mathrm{gt}, \mathrm{e}, s, t}+P_{\mathrm{wd}, s, t}+P_{\mathrm{dis}, s, t}-P_{\mathrm{ch}, s, t}= \\ P_{\mathrm{cal}, s, t}+P_{\mathrm{col}, s, t}+P_{\mathrm{rec}, s, t}+P_{\mathrm{load}, s, t} \end{array} $ | (37) |
式中:Ximax,Xjmax——设备i和j正常经济运行的最大容量;
Pimin,Pimax——设备i正常运行时的最小、最大输出功率;
Pi——设备i在t时段的实时功率;
Pgt,h,s,t,Pgt,e,s,t——场景s下t时段燃气轮机热输出功率和电输出功率;
Qh,s,t——场景s下t时段数据中心废热量;
Qload,s,t,Pload,s,t——数据中心综合能源系统在场景s下t时段的热负荷和电负荷;
Pwd,s,t——场景s下t时段的风电功率;
Pdis,s,t,Pch,s,t——场景s下t时段电储能设备的放电功率和充电功率;
Pcal,s,t,Pcol,s,t,Prec,s,t——场景s下t时段服务器功耗、制冷功耗、余热回收功耗。
3.2 CVaR风险管理
CVaR是基于一个给定置信水平下的条件概率分布,表示在所设定的置信度下,当投资损失超过给定的风险价值(Value at Risk,VaR)时可能遭受的潜在损失的平均值。给定置信度ε∈ (0,1),引入两个非负变量,分别为风险价值Rvar和φs[18]。φs为情景成本Ccost,s与Rvar的差值。如果Ccost,s<Rvar,则φs为零。上述关系可描述为
| $ R_{\mathrm{cvar}}=R_{\mathrm{var}}+\frac{1}{1-\varepsilon} \sum\limits_{s=1}^S p_s \varphi_s $ | (38) |
| $ R_{\text {var }} \geqslant 0 $ | (39) |
| $ \varphi_s \geqslant C_{\text {cost }, s}-R_{\mathrm{var}}, \varphi_s \geqslant 0 $ | (40) |
式中:Rcvar——条件风险价值。
采用CVaR作为风险管理方法,目标函数可以重写为

|
(41) |
式中:Ccr——使用CVaR进行风险管理的总成本;
β——风险规避因子,表示投资者的风险偏好。
CVaR风险管理约束条件为式(33)至式(41)。
3.3 RIRM风险管理
为描述可再生能源间歇性功率输出所带来的风险成本,本文提出了一种可再生能源间歇性风险度量方法(Renewable Intermittent Risk Method,RIRM)。其数学表达式为
| $ R_{\mathrm{rirm}}=\sum\limits_{s=1}^S \sum\limits_{t=1}^T p_s L_{\mathrm{int}} \Delta P_{\mathrm{bd}, s, t} $ | (42) |
| $ \left|\Delta P_{\mathrm{bd}, s, t}\right|=\left|P_{\mathrm{yc}, s, t}-P_{\mathrm{cj}, s, t}\right| $ | (43) |
| $ P_{\mathrm{yc}, s, t} \geqslant 0, P_{\mathrm{cj}, s, t} \geqslant 0 $ | (44) |
式中:Rrirm——可再生能源间歇性风险价值;
Lint——单位间歇性成本;
△Pbd,s,t——可再生能源预测发电量与实际发电量的差值;
Pyc,s,t,Pcj,s,t——可再生能源预测发电量和实际发电量。
采用RIRM作为风险管理方法,目标函数可以重写为
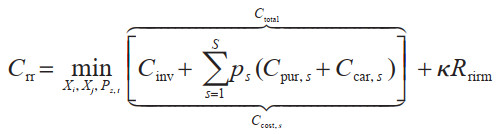
|
(45) |
| $ \kappa=1-\sqrt{\frac{1}{S} \ln \left(\frac{1}{1-\varepsilon}\right)} $ | (46) |
式中:Crr——使用RIRM进行风险管理的总成本;
κ——风险规避因子。
RIRM风险管理约束条件为式(33)至式(41)。
4 算例分析
4.1 算例参数及典型场景生成
为验证本文所提方法的经济性,选择中国北方某新建的大型数据中心作为案例进行仿真分析,所有费用均按年计算。算例仿真在配备i5- 7200U CPU和8 GB内存的电脑上进行,通过MATLAB 2018a软件编程实现。
数据中心园区级综合能源系统中需要规划的设备包括电制冷机、燃气轮机和余热回收装置,容量设置均为连续变量。调度时间间隔为1 h。计算碳排放因子相关输入参数如表 1所示。
表 1
计算碳排放因子相关输入参数
| 名称 | 电厂类型 | 容量/MW | 碳排放强度(kg/kWh) |
| G1 | 燃煤电厂 | 600 | 0.85 |
| G2 | 水电厂 | 150 | 0 |
| G3 | 燃气电厂 | 250 | 0.50 |
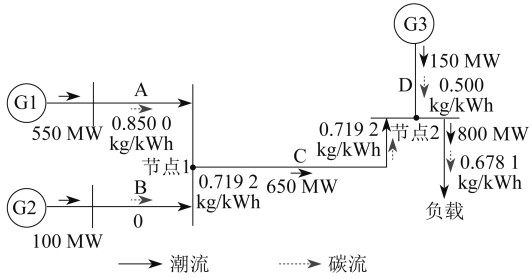
节点动态碳排放因子计算结果如图 3所示。
本文选取建筑用量最多、影响能耗较大的4种主要材料,相关参数如表 2所示。另外,EPS保温板消耗量为318 m2,对应碳排放因子为29.8 kg/m2,浪费率和运输至施工场地的距离分别为5%和57 km。为了保持计算的易处理性并保留负荷特征,采用K-means聚类方法生成典型日,共同确定电负荷和热负荷。所有拟安装能源设备的使用寿命和贴现率分别设为20 a和5%。
表 2
4种建材相关参数
| 建材类型 | 消耗量/kg | 碳排放因子/(kg/kg) | 浪费率/% | 距离/km |
| 钢筋 | 61 342.8 | 3.74 | 5 | 123 |
| 其他钢材 | 986.5 | 3.00 | 5 | 123 |
| 混凝土 | 220.3 | 0.92 | 5 | 65 |
| 沙子 | 181.6 | 0.21 | 5 | 99 |
针对本文构建的风险规避下面向建筑的数据中心综合能源系统规划模型,对3种情景进行算例仿真。情景1,不考虑风险度量方法和工作负载调度策略;情景2,考虑RIRM,不考虑工作负载调度策略;情景3,同时考虑RIRM和IT负载调度策略。
4.2 仿真结果分析
3种情景下的能源设备容量规划结果如表 3所示。
表 3
3种情景下能源设备容量规划结果
| 情景 | 燃气轮机 | 电制冷机 | 余热回收装置 |
| 1 | 7.24 | 4.34 | 2.44 |
| 2 | 6.57 | 12.49 | 5.63 |
| 3 | 6.56 | 11.78 | 5.96 |
由于数据中心的电能需求量相比热负荷更大,因此燃气轮机和电制冷机在规划容量中占比较高。数据中心在处理计算请求过程中消耗的电能都是以热的形式排出,余热回收装置可将这些低品位热源转换为用于供热的高品位热源,以提高数据中心的能源利用率。在情景2和情景3中,考虑RIRM,能源转换设备容量均有所增加,以防止在新能源供应不确定性受到较大影响时无法满足系统负荷需求。
3种情景下经济性指标如表 4所示。
表 4
3种情景下经济性指标
| 情景 | 投资成本 | 购能成本 | 碳排放成本 | 风险成本 | 总成本 |
| 1 | 0.691 8 | 63.640 4 | 4.384 8 | 0 | 68.717 0 |
| 2 | 0.705 0 | 62.500 0 | 4.343 0 | 0.401 1 | 67.949 1 |
| 3 | 0.703 4 | 62.284 8 | 4.341 4 | 0.389 6 | 67.719 2 |
情景1不考虑风险度量方法,因此风险成本为零。将情景1作为比较基线,情景3的系统总成本最低,下降了1.452%。在同一风险度量方法下,情景3总成本低于情景2,说明所提出的动态减碳方法降低了系统成本。
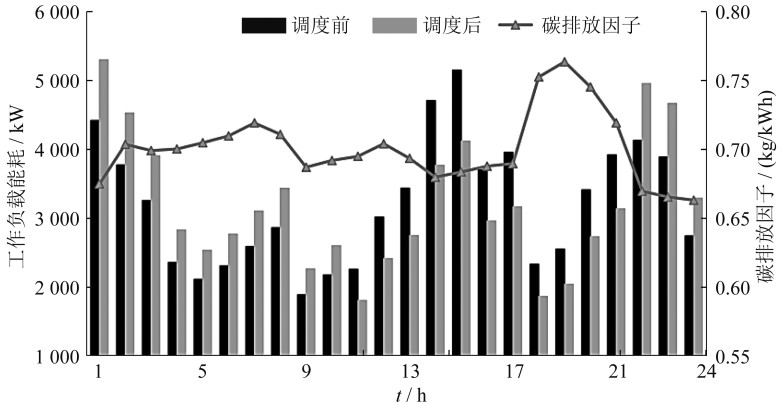
动态减碳策略使用前后的系统能耗如图 4所示。当碳排放因子数值较高时,在满足请求服务质量基础上,该时刻数据中心的能耗相应下降,表明数据中心在这一时刻减少了工作负载量,即能源使用量降低,碳排放量也相应减少。
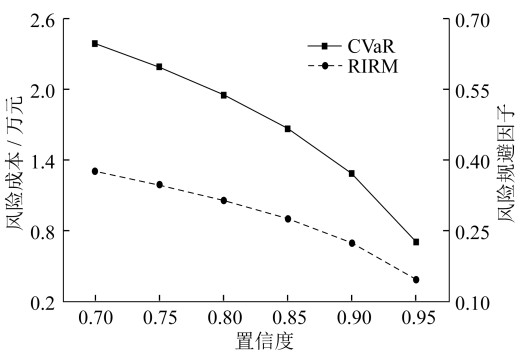
由于CVaR方法的置信水平和风险规避因子是相互独立的,为保证实验的严谨性,使CVaR的置信水平和风险规避因子与RIRM相同。风险度量参数(即置信度和风险规避因子)对风险成本的影响如图 5所示。
由图 5可知,在相同的置信水平和风险规避因子下,RIRM和CVaR的风险成本走势相同。这表明两种方法在规避风险时,都注意概率低、影响大的极端事件。然而,与只注重尾部风险的CVaR方法相比,本文提出的RIRM在风险度量中综合考虑了不同场景的影响,并对场景概率较低的情况进行了更为谨慎的估计,从而使得RIRM的风险成本平均降低了45.54%,表明RIRM在处理可再生能源间歇性功率输出不确定性上有更好的适应性。
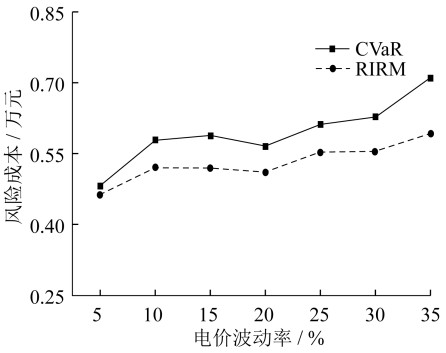
对比CVaR和RIRM在不同程度电价波动率下的风险成本,结果如图 6所示。
由图 6可以看出,在整体走势上,随着电价波动率的增大,风险成本随之增加。CVaR的走势更陡峭,而RIRM的变化较为平缓,表明在电价波动程度较大时,RIRM相对更稳定,而CVaR的灵敏度更高,即RIRM方法更适用于风险管理,而CVaR则适用于对风险变化更为敏感的情况。
5 结语
本文研究了面向建筑的数据中心综合能源系统,并以总成本和碳排放最小化为目标,提出了一种基于动态碳排放因子的低碳控制策略。结果显示,所提方法的碳排放和系统总成本均有所降低。当电价波动程度较大时,RIRM能够提供更可靠的风险估计,而CVaR则适用于对风险变化更为敏感的情况。所提出的规划方法可为园区级综合能源系统投资者了解园区自身建筑的碳排放,以及新能源接入园区带来的风险提供参考。未来将针对不同地理位置互联的数据中心,开展动态碳排放因子的优化调度研究。
参考文献
-
[1]胡博, 孙铠彬, 邵常政, 等. 面向全过程碳足迹的园区综合能源系统碳感知与优化方法[J]. 高电压技术, 2022, 48(7): 2495-2504.
-
[2]丁肇豪, 曹雨洁, 张素芳, 等. 能源互联网背景下数据中心与电力系统协同优化(一): 数据中心能耗模型[J]. 中国电机工程学报, 2022, 42(9): 3161-3176.
-
[3]IBRAHIM A, NOSHY M, ALI H A, et al. PAPSO: a poweraware VM placement technique based on particle swarm optimization[J]. IEEE Access, 2020, 8: 81747-81764. DOI:10.1109/ACCESS.2020.2990828
-
[4]LI J, BAO Z, LI Z Y. Modeling demand response capability by internet data centers processing batch computing jobs[J]. IEEE Transactions on Smart Grid, 2015, 6(2): 737-747. DOI:10.1109/TSG.2014.2363583
-
[5]QURESHI A, WEBER R, BALAKRISHNAN H, et al. Cutting the electric bill for internet-scale systems[J]. ACM SIGCOMM Computer Communication Review, 2009, 39(4): 123-134. DOI:10.1145/1594977.1592584
-
[6]CUPELLI L, SCHÜTZ T, JAHANGIRI P, et al. Data center control strategy for participation in demand response programs[J]. IEEE Transactions on Industrial Informatics, 2018, 14(11): 5087-5099. DOI:10.1109/TII.2018.2806889
-
[7]王玚, 李鹏, 冀浩然, 等. 考虑多类型资源的数据中心园区供电协调规划[J]. 电力系统自动化, 2022, 46(14): 19-28.
-
[8]LYU J W, ZHANG S X, CHENG H Z, et al. Optimal sizing of energy station in the multienergy system integrated with data center[J]. IEEE Transactions on Industry Applications, 2021, 57(2): 1222-1234. DOI:10.1109/TIA.2021.3054607
-
[9]QI W B, LI J, LIU Y Q, et al. Planning of distributed internet data center microgrids[J]. IEEE Transactions on Smart Grid, 2019, 10(1): 762-771. DOI:10.1109/TSG.2017.2751756
-
[10]NGUYEN K K, CHERIET M, LEMAY M, et al. Powering a data center network via renewable energy: a green testbed[J]. IEEE Internet Computing, 2013, 17(1): 40-49. DOI:10.1109/MIC.2012.125
-
[11]DING Z H, XIE L Y, LU Y, et al. Emission-aware stochastic resource planning scheme for data center microgrid considering batch workload scheduling and risk management[J]. IEEE Transactions on Industry Applications, 2018, 54(6): 5599-5608. DOI:10.1109/TIA.2018.2851516
-
[12]YU L, JIANG T, CAO Y, et al. Risk-constrained operation for internet data centers in deregulated electricity markets[J]. IEEE Transactions on Parallel and Distributed Systems, 2014, 25(5): 1306-1316. DOI:10.1109/TPDS.2013.2297095
-
[13]杜刚, 赵冬梅, 刘鑫. 计及风电不确定性优化调度研究综述[J]. 中国电机工程学报, 2023, 43(7): 2608-2626.
-
[14]郭立邦, 丁一, 包铭磊, 等. 两级电力市场环境下计及风险的省间交易商最优购电模型[J]. 电网技术, 2019, 43(8): 2726-2733.
-
[15]NOTTON G, NIVET M L, VOYANT C, et al. Intermittent and stochastic character of renewable energy sources: consequences, cost of intermittence and benefit of forecasting[J]. Renewable and Sustainable Energy Reviews, 2018, 87: 96-105. DOI:10.1016/j.rser.2018.02.007
-
[16]周世博, 周明, 孙黎滢, 等. 激发多元灵活性的数据中心协同优化运行方法[J]. 电网技术, 2024, 48(6): 1-13.
-
[17]周天睿, 康重庆, 徐乾耀, 等. 电力系统碳排放流分析理论初探[J]. 电力系统自动化, 2012, 36(7): 38-43.
-
[18]GEBRESLASSIE B H, YAO Y, YOU F Q. Design under uncertainty of hydrocarbon biorefinery supply chains: multiobjective stochastic programming models, decomposition algorithm, and a comparison between CVaR and downside risk[J]. AIChE Journal, 2012, 58(7): 2155-2179.