|
|
|
发布时间: 2024-08-28 |
综合能源 |
|
|
|
收稿日期: 2024-04-22
中图法分类号: TM73
文献标识码: A
文章编号: 2096-8299(2024)04-0355-10
|
摘要
为提升综合能源系统(IES)中可再生能源的消纳以及实现低碳排放,提出了一种多时间尺度下考虑需求响应和电转气-碳捕集系统(P2G-CCS)耦合的综合能源系统低碳调度策略。首先,建立了含P2G-CCS耦合和考虑电冷热负荷需求响应的IES数学模型。其次,建立了阶梯碳交易模型对碳排放量进行约束。最后,提出了源荷互补的IES多时间尺度低碳调度策略,构建了以购气和煤耗成本、碳封存成本、碳交易成本、机组启停成本和弃风弃光成本为目标函数的日前-日内-实时调度模型。算例结果表明,所提模型有效提高了IES的经济效益、低碳效益和能源利用率。
关键词
电转气; 综合能源系统; 多时间尺度; 需求响应
Abstract
In order to enhance the consumption of renewable energy in integrated energy systems(IES)and achieve low-carbon emissions, this paper proposes a low-carbon scheduling strategy for integrated energy systems that considers demand response and power to gas and carbon capture system(P2G-CCS)coupling at multiple time scales. Firstly, an IES mathematical model with P2G-CCS coupling and considering load side demand response was established. Secondly, a tiered carbon trading model was established to constrain carbon emissions. Finally, a multi-time scale low-carbon scheduling strategy for IES with complementary sources and loads is proposed, and a daily intraday real-time scheduling model is constructed with gas and coal consumption costs, carbon storage costs, carbon trading costs, unit start-up and shutdown costs, and wind and solar curtailment costs as objective functions. The calculation results show that the proposed model effectively improves the economic benefits, low-carbon benefits, and energy utilization efficiency of IES.
Key words
power to gas; integrated energy system; multiple time scales; demand response
随着经济与社会的发展,传统能源消耗加剧了环境污染,国内能源转型面临挑战[1]。综合能源系统(Integrated Energy System,IES)由于能够耦合电网、热网和气网并能够梯级利用能源,成为达成“双碳”目标的重要举措[2]。碳捕集系统(Carbon Capture System,CCS)作为一种低碳化技术,由于能够将捕集和封存的CO2作为电转气(Power to Gas,P2G)反应过程中的优质碳原料,因此与P2G结合,为IES的低碳经济运行提供了基础[3]。
针对P2G-CCS耦合的IES协同运行,文献[4]构建了含P2G-CCS的多目标优化模型,利用粒子群算法配合模糊综合评价法进行求解,提高了能源利用效率。文献[5]建立了含储液罐的P2G-CCS联合运行的IES模型,将储液罐作为CO 2与IES系统连接时的缓冲站,降低了碳排放量并促进了风电消纳。文献[6]构建了含P2G-CCS的风电、光伏、火力发电、储能一体化系统架构,对电能流及碳流的运行特性进行了详细的建模,实现了综合利益最大化,降低了碳排放量。然而上述文献仅从设备耦合及能源低碳利用的角度分析含P2G-CCS的IES调度,没有考虑碳排放的环境成本及负荷侧的需求响应对IES的调度影响。随着“双碳”目标的提出,碳排放交易市场应运而生,碳交易机制建设为IES低碳化运行提供了有效途径。文献[7-8]引入阶梯式碳交易机制约束碳排放,建立了考虑氢燃料电池与燃气轮机联合运行的热电联产模型,提高了IES能源消纳率。文献[9]提出了碳交易机制下P2G及负荷柔性特征的IES低碳经济调度策略,并利用负荷侧的柔性调度,缓解了用能高峰时段的供能压力,提高了系统的运行效益。然而上述文献没有考虑IES系统内分布式能源输出功率的不确定性,在实际调度中往往产生偏差。随着高比例可再生能源的接入,因IES运行而增加的不确定性风险不容忽视,研究多时间尺度优化调度策略具有重要意义[10]。文献[11]提出了多时间尺度下P2G-CCS综合能源调度策略,在荷侧分析了不同时间尺度下的响应特性,构建了日前-日内-实时调度模型,实现了系统经济运行。文献[12]提出了基于广义储能的IES多时间尺度模型,简化了能源调度与消费之间的信息交互,降低了电力系统的运营成本。文献[13-14]研究了电、气、热负荷的可调度特性以及在不同时间尺度下的响应差异性,建立了综合运行成本最低的日内滚动优化调度模型。上述文献着重研究了时间维度上各机组达到最佳运行工况的优化策略,而在降低碳排放、可再生能源消纳方面考虑不多。
针对上述问题,本文从低碳技术和能源消纳出发,建立了P2G-CCS耦合的IES多时间尺度优化调度模型,综合考虑了需求侧响应、阶梯式碳交易机制对IES系统的调度影响。以购气和煤耗成本、封存成本、机组启停成本、碳交易成本和弃风成本之和最小为目标函数,建立日前-日内-实时调整优化模型,并通过算例验证本文模型的有效性。
1 基于阶梯碳交易的P2G-CCS耦合的IES调度模型
1.1 P2G-CCS耦合的IES调度模型结构
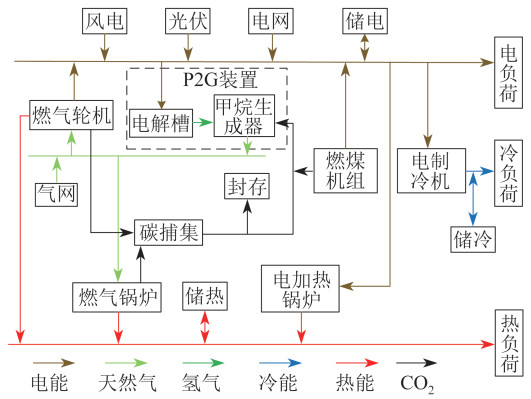
本文研究的P2G-CCS耦合的IES调度模型结构如图 1所示。其中负荷包括电、冷、热负荷,电负荷由燃气轮机、燃煤机组、风电和光伏发电(以下简称“风光”)提供;热负荷由燃气轮机、燃气锅炉和电加热锅炉供应;冷负荷由电制冷机提供。
1.2 P2G-CCS耦合模型
燃煤机组、燃气锅炉、燃气轮机均有CO2产生,CCS与P2G耦合能够有效减少碳排放量。本文在CCS系统加装储液设备,能够解除CO2吸收和再生过程的耦合。储液设备模型参考文献[3],其中,富液与CO2的关系表示为
| $ \left\{\begin{array}{l} 25 v_{\mathrm{F}, \text { in }}^t=\frac{\eta_{\mathrm{c}} E_1^t}{\rho_{\mathrm{co_2}}} \\ 25 v_{\mathrm{F}, \text { out }}^t=\frac{E_2^t}{\rho_{\mathrm{co_2}}} \end{array}\right. $ | (1) |
式中:vtF,in,vtF,out——t时刻流进和流出富液存储器的体积流量;
ηc——碳捕集效率;
E1t——t时刻CCS吸收的CO2质量;
E2t——t时刻碳捕集再生塔处理的CO2质量;
ρco2——CO2密度。
CCS能耗主要包括运行能耗和固定能耗。P2G-CCS耦合模型表示为
| $ \left\{\begin{array}{l} P_{\mathrm{CCS}, \text { sum }}^t=P_{\mathrm{CCS}}^t+P_{\mathrm{B}} \\ P_{\mathrm{CCS}}^t=e_{\mathrm{c}} E_2^t \\ E_1^t=E^t-e_1^t \\ Q_{\mathrm{EL}, \mathrm{H} 2}^t=\eta_{\mathrm{EL}} P_{\mathrm{EL}}^t \\ Q_{\mathrm{H} 2 \mathrm{G}, \text { out }}^t=\eta_{\mathrm{H} 2 \mathrm{G}} Q_{\mathrm{H} 2 \mathrm{G}, \text { in }}^t \\ E_{2, \mathrm{H} 2 \mathrm{G}}^t=3\;600 Q_{\mathrm{H} 2 \mathrm{G}, \text { out }}^t \frac{\rho_{\mathrm{co}_2}}{L_{\mathrm{CH}_4}} \\ E_2^t=E_{2, \mathrm{H} 2 \mathrm{G}}^t+E_{2, \text { storage }}^t \end{array}\right. $ | (2) |
式中:PtCCS,sum——t时刻CCS总能耗;
PCCSt——t时刻运行能耗;
PB——固定能耗;
ec——处理单位质量的CO2能耗;
Et——t时刻机组CO2总排放量;
et1——t时刻烟气分流进入大气的CO2量;
QtEL,H2——t时刻电解的产氢功率;
PELt——t时刻电解消耗的电功率;
QtH2G,out,QtH2G, in——t时刻甲烷化设备产出天然气的功率和耗氢功率;
ηEL,ηH2G——甲烷化和电转氢效率;
E2t,H2G——t时刻CCS中甲烷化CO2利用量;
LCH4——天然气热值;
E2t,storage——t时刻CCS封存的CO2量。
1.3 能量转化设备模型
燃气轮机模型为
| $ \left\{\begin{array}{l} P_{\mathrm{PH}}^t=P_{\mathrm{CHP}}^t+H_{\mathrm{CHP}}^t \\ P_{\mathrm{CHP}}^t=\eta_{\mathrm{chp}, \mathrm{P}} P_{\mathrm{CHP}, \mathrm{gt}}^t \\ H_{\mathrm{CHP}}^t=\eta_{\mathrm{chp}, \mathrm{H}} P_{\mathrm{CHP}, \mathrm{gt}}^t \end{array}\right. $ | (3) |
式中:PPHt,PCHPt,HCHPt——t时刻燃气轮机的总输出功率、产电和产热功率;
ηchp,P,ηchp,H——燃气轮机的电、热效率;
PtCHP,gt——t时刻燃气轮机消耗的气功率。
燃气轮机运行功率约束与爬坡约束条件为
| $ \left\{\begin{array}{l} P_{\mathrm{CHP}, \min }^t \leqslant P_{\mathrm{CHP}}^t \leqslant P_{\mathrm{CHP}, \max }^t \\ H_{\mathrm{CHP}, \min } \leqslant H_{\mathrm{CHP}}^t \leqslant H_{\mathrm{CHP}, \max } \\ \Delta P_{\mathrm{PH}}^{\mathrm{d}} \leqslant P_{\mathrm{PH}}^t-P_{\mathrm{PH}}^{t-1} \leqslant \Delta P_{\mathrm{PH}}^{\mathrm{up}} \end{array}\right. $ | (4) |
式中:PCHP,maxt,PCHP,mint——t时刻燃气轮机组电输出功率上、下限;
HCHP,min,HCHP,max——燃气轮机组热输出功率上、下限;
△PPHup,△PPHd——燃气轮机组输出功率爬坡上、下限。
燃煤机组的运行功率约束条件和爬坡约束条件与燃气轮机相类似,本文不再赘述。
燃气锅炉是通过燃气产生热能的高碳排放设备,模型表示为
| $ \left\{\begin{array}{l} H_{\mathrm{GB}}^t=\eta_{\mathrm{GB}} P_{\mathrm{GB}, \mathrm{gt}}^t \\ H_{\mathrm{GB}, \min } \leqslant H_{\mathrm{GB}}^t \leqslant H_{\mathrm{GB}, \max } \\ \Delta H_{\mathrm{GB}}^{\mathrm{d}} \leqslant H_{\mathrm{GB}}^t-H_{\mathrm{GB}}^{t-1} \leqslant \Delta H_{\mathrm{GB}}^{\mathrm{up}} \end{array}\right. $ | (5) |
式中:HGBt,HGBt-1——t、t-1时刻燃气锅炉产热功率;
ηGB——燃气锅炉热效率;
PtGB,gt——t时刻燃气锅炉耗气功率;
HGB,min,HGB,max——燃气锅炉输出功率下限和上限;
ΔHGBup,ΔHGBd——燃气锅炉输出功率爬坡上、下限。
电加热锅炉能将电能转化为热能,其模型表示为
| $ \left\{\begin{array}{l} H_{\mathrm{EB}}^t=\eta_{\mathrm{EB}} P_{\mathrm{EB}, \mathrm{gt}}^t \\ H_{\mathrm{EB}, \min } \leqslant H_{\mathrm{EB}}^t \leqslant H_{\mathrm{EB}, \max } \\ \Delta H_{\mathrm{EB}}^{\mathrm{d}} \leqslant H_{\mathrm{EB}}^t-H_{\mathrm{EB}}^{t-1} \leqslant \Delta H_{\mathrm{EB}}^{\mathrm{up}} \end{array}\right. $ | (6) |
式中:HEBt,HEBt-1——t、t-1时刻电加热锅炉产热功率;
ηEB——电加热锅炉能量转化效率;
PEB,gtt——t时刻电加热锅炉耗电功率;
HEB,max,HEB,min——电热锅炉输出功率上、下限;
△HEBup,△HEBd——电热锅炉输出功率爬坡上、下限。
电制冷机通过压缩、膨胀过程将电能转化为冷能。其模型表示为
| $ \left\{\begin{array}{l} P_{\mathrm{ERU}}^t=\eta_{\mathrm{ERU}} P_{\mathrm{ERU}, \mathrm{gt}}^t \\ P_{\mathrm{ERU}, \min } \leqslant P_{\mathrm{ERU}}^t \leqslant P_{\mathrm{ERU}, \max } \\ \Delta P_{\mathrm{ERU}}^{\mathrm{d}} \leqslant P_{\mathrm{ERU}}^t-P_{\mathrm{ERU}}^{t-1} \leqslant \Delta P_{\mathrm{ERU}}^{\text {up }} \end{array}\right. $ | (7) |
式中:PERUt,PERUt-1——t、t-1时刻电制冷机输出功率;
ηERU——电制冷机能量转化效率;
PERU,gtt——t时刻电制冷机耗电功率;
PERU,max,PERU,min——电制冷机输出功率上、下限;
△PERUup,△PERUd——电制冷机输出功率爬坡上、下限。
1.4 储能模型
本文储能系统包括储电、储热和储冷系统,储电、储热、储冷设备作为IES系统的灵活性资源,能够满足系统实时平衡及灵活经济调度要求。储能系统约束模型表示为
| $ \left\{\begin{array}{l} S_x^t=S_x^{t-1}\left(1-\delta_x\right)+\left(P_{x, \text { cha }}^t \eta_{x, \text { cha }}-\frac{P_{x, \text { dis }}^t}{\eta_{x, \text { dis }}^t}\right) \Delta t \\ S_x^1=S_x^{24} \\ S_{x, \text { min }}^2 \leqslant S_x^t \leqslant S_{x, \text { max }} \\ \lambda_{x, \text { chas }}^t P_{x, \text { cha }}^{\min } \leqslant P_{x, \text { cha }}^t \leqslant \lambda_{x, \text { cha }}^t P_{x, \text { cha }}^{\max } \\ \lambda_{x, \text { dis }}^t P_{x, \text { dis }}^{\min } \leqslant P_{x, \text { dis }}^t \leqslant \lambda_{x, \text { dis }}^t P_{x, \text { dis }}^{\max } \\ \lambda_{x, \text { cha }}^t \lambda_{x, \text { dis }}^t \leqslant 1 \end{array}\right. $ | (8) |
式中:Sxt,Sxt-1——t、t-1时刻的存储能量;
x——储能类型,包括电能、热能、冷能;
δx——储能设备自损系数;
Pxt,cha,Pxt,dis——t时刻储能设备充、放能功率;
ηx,cha,ηx,dis——储能设备充、放能效率;
△t——调度周期内单位时间间隔,1 h;
Sx,max,Sx,min——储能设备容量上、下限;
λtx,cha,λtx,dis——t时刻充、放能状态,0-1变量,λtx,cha取1时充能,λtx,dis取1时放能;
Px,chamax,Px,chamin——充能上、下限;
Px,dismax,Px,dismin——放能上、下限。
1.5 需求响应模型
1.5.1 可转移负荷
可转移负荷在负荷运行过程中可以中断,且能够转移到其他时间段运行,但累计运行总时长不变。其运行约束条件为
| $ \left\{\begin{array}{l} P_{x, \mathrm{tr}}^t=P_{\mathrm{N}, \mathrm{tr}} I_{\mathrm{tr}}^t \\ \sum\limits_{i=1}^n I_{\mathrm{tr}}^t=T_{\mathrm{tr}} \end{array}\right. $ | (9) |
式中:Pxt,tr——t时刻可转移负荷运行功率;
PN,tr——可转移负荷额定功率;
Itrt——可转移负荷在t时刻的运行状态,0-1变量,取1时可以转移,取0时不可以转移;
Ttr——可转移负荷运行时间总和。
1.5.2 可削减负荷
可削减负荷根据调度需求对相应的负荷进行削减。为保证负荷削减的合理性,对削减次数以及削减时间做相应约束。约束条件为
| $ \left\{\begin{array}{l} B_{x, \text { cut }}^t P_{x, \text { cun }}^{\min } \leqslant P_{x, \text { cut }}^t \leqslant B_{x, \text { cut }}^t P_{x, \text { cut }}^{\max } \\ t_{\text {cut }, \min } \leqslant \sum\limits_{t=1}^{t+t_{cl} /-1} B_{x, \mathrm{cut}}^t \leqslant t_{\mathrm{cut}, \max } \\ \sum\limits_{t=1}^{24} B_{x, \mathrm{cut}}^t \leqslant B_{x, \max } \end{array}\right. $ | (10) |
式中:Bxt,cut——t时刻负荷削减状态,0-1变量,削减时取1;
Px,cutmax,Px,cutmin——可削减负荷上、下限;
Pxt,cut——t时刻削减功率;
Bx,max——最大削减次数;
tcut,max,tcut,min——连续削减时长上、下限;
tcl——削减时长。
由式(9)和式(10)得到各时间段电、热、冷负荷为
| $ P_{x, \mathrm{~L}}^t=P_{x, \mathrm{~b}}^t+P_{x, \mathrm{tr}}^t-P_{x, \mathrm{cut}}^t $ | (11) |
式中:Px,Lt,Px,bt——t时刻总负荷和基础负荷。
2 阶梯碳交易机制
2.1 实际碳排放量
本文的系统碳排放总量Et包含火电机组、燃气锅炉和燃气轮机产生的CO2,表示为
| $ E^t=\mu_1\left(P_{\mathrm{CHP}, \mathrm{gt}}^t+P_{\mathrm{GB}, \mathrm{gt}}^t\right)+\mu_2 P_{\text {fire }}^t $ | (12) |
式中:μ1,μ2——机组消耗单位天然气对应的碳排放量和火电机组碳排放强度;
Pfiret——t时刻火电机组发电量。
本文实际碳排放量由Et减去封存及P2G过程中减少的CO2,表示为
| $ E_{\mathrm{j}}^t=E^t-\mu_{\mathrm{c}} E_1^t $ | (13) |
式中:Ejt——t时刻净碳排放量;
μc——CCS装置运行效率。
2.2 碳排放权配额
本文碳排放权配额包含燃气机组供电、供热共同分配的额度和燃煤机组的碳排放权配额,表示为
| $ E_{\mathrm{IES}}^t=\omega_{\mathrm{P}} P_{\mathrm{CHP}}^t+\omega_{\mathrm{H}} H_{\mathrm{CHP}}^t+\omega_{\text {fire }} P_{\text {fire }}^t $ | (14) |
式中:EtIES——t时刻IES总碳排放权配额;
ωP,ωH,ωfire——燃气机组单位供电、供热功率的碳排放权配额和燃煤机组单位供电功率的碳排放权配额。
参与碳交易市场的实际配额Ert为
| $ E_{\mathrm{r}}^t=E_{\mathrm{j}}^t-E_{\mathrm{HS}}^t $ | (15) |
2.3 基于阶梯式机制的碳交易成本模型
阶梯式碳交易模型[15]表示为
| $ G_{\mathrm{CO}_2}^t= \begin{cases}b E_{\mathrm{r}}^t, & E_{\mathrm{r}}^t \leqslant d \\ b(1+\alpha)\left(E_{\mathrm{r}}^t-d\right)+b d, & d \leqslant E_{\mathrm{r}}^t \leqslant 2 d \\ b(1+2 \alpha)\left(E_{\mathrm{r}}^t-2 d\right)+b(2+\alpha) d, & 2 d \leqslant E_{\mathrm{r}}^t \leqslant 3 d \\ b(1+3 \alpha)\left(E_{\mathrm{r}}^t-3 d\right)+b(3+3 \alpha) d, & 3 d \leqslant E_{\mathrm{r}}^t \leqslant 4 d \\ b(1+4 \alpha)\left(E_{\mathrm{r}}^t-4 d\right)+b(4+6 \alpha) d, & 4 d \leqslant E_{\mathrm{r}}^t\end{cases} $ | (16) |
式中:GtCO2——碳交易成本;
b——碳交易基价;
d——碳排放量区间长度;
α——价格增长率。
3 多时间尺度优化模型
3.1 多时间尺度优化调度模型
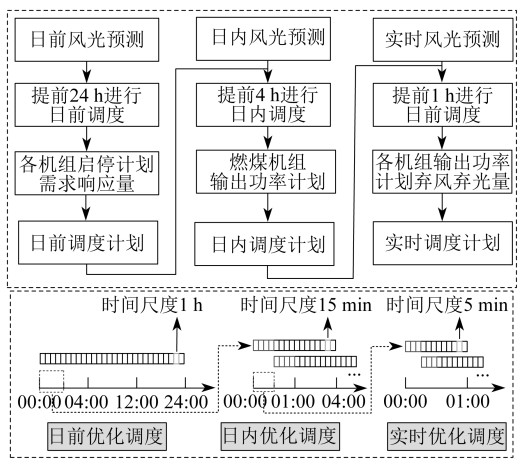
由于IES内风光输出功率的不确定性,日前做出的调度往往会与实际调度产生偏差。针对这一问题,本文提出日前-日内-实时的多时间尺度优化调度。多时间尺度优化调度模型如图 2所示。
在日前阶段,以风光预测数据为基础,计算出各机组的启停计划、设备输出功率、碳排放及需求响应量,并将启停计划和需求响应量代入日内模型。在日内阶段,利用滚动优化缩短预测周期,在日前调度基础上调整设备输出功率及新能源弃用量,并将燃煤机组输出功率计划代入实时模型。在实时调整阶段,以5 min为时间尺度对日内计算结果再优化,计算出设备的实时输出功率计划及弃风、弃光量。
3.2 日前调度模型
日前调度阶段以经济成本及碳交易成本最低为目标函数。其公式为
| $ \left\{\begin{aligned} \min F= & C_{\mathrm{CO}_2}+C_{\mathrm{f}}+C_{\text {fire }}+C_{\text {buy }}+C_{\text {cur }} \\ C_{\mathrm{CO}_2}= & \sum\limits_{t=1}^T G_{\mathrm{CO} 2}^t \\ C_{\mathrm{f}}= & \sum\limits_{t=1}^T \varphi_{\text {storage }} E_{2, \text { storage }}^t \\ C_{\text {fire }}= & \varphi_{\text {fire }} \sum\limits_{t=1}^T\left[\lambda_{\text {fire }}^t\left(1-\lambda_{\text {fire }}^{t-1}\right)+\lambda_{\text {fire }}^{t-1}\left(1-\lambda_{\text {fire }}^t\right)\right]+ \\ & \sum\limits_{t=1}^T\left[a_{\text {fire }}\left(P_{\text {fire }}^t\right)^2+b_{\text {fire }} P_{\text {fire }}^t+c_{\text {fire }}\right] \\ C_{\text {buy }}= & \sum\limits_{t=1}^T \varphi_{\text {buy }} Q_{\text {buy }}^t \\ C_{\text {cur }}= & \sum\limits_{t=1}^T \varphi_{\text {cur }}\left(P_{\text {cur, Wind }}^t+P_{\text {cur, PV }}^t\right) \end{aligned}\right. $ | (17) |
式中:F——总成本;
CCO2,Cf,Cfire,Cbuy,Ccur——碳交易成本、碳封存成本、燃煤机组启停煤耗成本、购气成本、弃用风光成本。
T——调度周期;
φstorage,φfire,φbuy,φcur——单位封存成本系数、启停成本系数、购气成本系数、弃风和弃光单位惩罚成本系数。
λfiret,λfiret-1——t、t-1时刻燃煤机组启停状态,0-1变量,启动取1;
Qtbuy——t时刻购入天然气量;
afire,bfire,cfire——燃煤机组的二次项、一次项、常数项煤耗成本系数;
Pcur,Windt,Pcur,PVt——弃用风电、光伏发电功率。
日前调度模型约束除各机组相关约束外,还包括电、热、冷功率平衡约束及气平衡约束。约束条件为
| $ \left\{\begin{array}{l} P_{\mathrm{Wind}}^t+P_{\mathrm{PV}}^t+P_{\text {fire }}^t+P_{\mathrm{CHP}}^t+P_{\mathrm{e}, \text { dis }}^t=P_{\mathrm{EB}, \mathrm{gt}}^t+ \\ P_{\mathrm{EL}}^t+P_{\mathrm{e}, \mathrm{L}}^t+P_{\mathrm{cCS}, \mathrm{sum}}^t+P_{\mathrm{e}, \mathrm{cha}}^t+P_{\mathrm{ERU}, \mathrm{gt}}^t \\ H_{\mathrm{CHP}}^t+H_{\mathrm{EB}}^t+P_{\mathrm{h}, \mathrm{dis}}^t=P_{\mathrm{h}, \mathrm{L}}^t+P_{\mathrm{h}, \text {, ha }}^t \\ P_{\mathrm{ERU}}^t+P_{\mathrm{d}, \mathrm{dis}}^t=P_{\mathrm{d}, \mathrm{L}}^t+P_{\mathrm{d}, \mathrm{cha}}^t \\ P_{\mathrm{CHP}, \mathrm{gt}}^t+P_{\mathrm{GB}, \mathrm{gt}}^t=Q_{\mathrm{HZG}, \mathrm{out}}^t+Q_{\text {buy }}^t \end{array}\right. $ | (18) |
式中:PWindt,PPVt——t时刻风电、光伏预测输出功率;
Pe,Lt,Ph,Lt,Pd,Lt——t时刻电能、热能、冷能负荷;
Pe,dist,Pe,chat——t时刻电能设备放、充电功率;
Ph,dist,Ph,chat——t时刻热能设备放、充电功率;
Pd,dist,Pd,chat——t时刻冷能设备放、充电功率。
日前调度后,将部分结果作为确定量代入日内调度中,包括各机组的启停计划、各时刻需求响应量。
3.3 日内调度模型
日内调度阶段以15 min为时间尺度,提前4 h预测风光数据。与日前阶段相比,日内调度阶段不考虑各机组启停成本和需求响应量。日内调度的目标函数为
| $ \left\{\begin{array}{l} \min F=C_{\mathrm{CO}_2}+C_{\mathrm{f}}+C_{\text {fire }}+C_{\text {buy }}+C_{\text {cur }} \\ C_{\text {fire }}=\sum\limits_{t=1}^T a_{\text {fire }}\left(P_{\text {fire }}^t\right)^2+b_{\text {fire }} P_{\text {fire }}^t+c_{\text {fire }} \end{array}\right. $ | (19) |
日内阶段的相应约束条件与日前阶段相类似。由于随着时间维度的变化,时间尺度从1 h变为15 min,因此相关能源转换设备的爬坡约束条件需进行一定的调整。
日内调度模型的约束条件包括式(1)至式(16),其中式(4)至式(7)中的爬坡约束条件因时间尺度变化需作相应调整,表示为
| $ \left\{\begin{array}{l} \frac{\Delta P_{\mathrm{PH}}^{\mathrm{d}}}{4} \leqslant P_{\mathrm{PH}}^t-P_{\mathrm{PH}}^{t-1} \leqslant \frac{\Delta P_{\mathrm{PH}}^{\mathrm{up}}}{4} \\ \frac{\Delta H_{\mathrm{GB}}^{\mathrm{d}}}{4} \leqslant H_{\mathrm{GB}}^t-H_{\mathrm{GB}}^{t-1} \leqslant \frac{\Delta H_{\mathrm{GB}}^{\mathrm{up}}}{4} \\ \frac{\Delta H_{\mathrm{EB}}^{\mathrm{d}}}{4} \leqslant H_{\mathrm{EB}}^t-H_{\mathrm{EB}}^{t-1} \leqslant \frac{\Delta H_{\mathrm{EB}}^{\mathrm{up}}}{4} \\ \frac{\Delta P_{\mathrm{ERU}}^{\mathrm{d}}}{4} \leqslant P_{\mathrm{ERU}}^t-P_{\mathrm{ERU}}^{t-1} \leqslant \frac{\Delta P_{\mathrm{FRU}}^{\mathrm{up}}}{4} \end{array}\right. $ | (20) |
日内阶段调度后,可将各能源转化设备、储能系统、燃煤机组的输出功率计划代入到实时阶段进行计算。
3.4 实时调度模型
实时调度阶段以5 min为时间尺度,将日内确定的能源转换设备、火电机组输出功率及储能充、放能功率代入实时调度进行优化。由于新能源存在预测误差,而CCS系统具备较快响应速度,可实时参与深度调节,提高实时调度中风电消纳和功率波动的平抑。实时阶段不考虑燃煤机组的煤耗成本和各能源转化设备相关成本,仅考虑利用CCS系统平衡系统波动成本。相关目标函数为
| $ \min F=C_{\mathrm{CO}_2}+C_{\mathrm{f}}+C_{\text {buy }}+C_{\mathrm{cur}} $ | (21) |
与日内调度类似,相关约束也因时间维度的变化而产生变化,此处不再赘述。实时阶段相关碳捕集功率调节约束条件为
| $ \left\{\begin{array}{l} \Delta P_{\mathrm{BS}, \mathrm{CCS}}^t=P_{\mathrm{CCS}}^t \\ \Delta P_{\mathrm{BX}, \mathrm{CCS}}^t=P_{\mathrm{B}, \mathrm{CCS}}^{\max }-P_{\mathrm{CCS}}^t \end{array}\right. $ | (22) |
式中:△PtBS,CCS,△PtBX,CCS——t时刻碳捕集机组的净输出功率实时上调、下调限值;
PB,CCSmax——碳捕集电厂的再生塔和压缩机所允许的最大运行能耗。
碳捕集机组一般使用溶液存储器对产生的能耗进行转移,应满足碳捕集系统净输出功率调节量在相应调节范围内。其表达式为
| $ -\sum\limits_{t=1}^{288} \Delta P_{\mathrm{BX}, \mathrm{CCS}}^t \leqslant \sum\limits_{t=1}^{288} \Delta P_{\mathrm{BJ}, \mathrm{CCS}}^t \leqslant \sum\limits_{t=1}^{288} \Delta P_{\mathrm{BS}, \mathrm{CCS}}^t $ | (23) |
式中:△PBJ,CCSt——t时刻碳捕集机组净输出功率实时调整量。
4 仿真分析
4.1 算例数据
本文的IES系统包含1个风电厂、1个CCS、1台燃气锅炉、台1P2G设备、台燃煤机组、台电11加热锅炉、1台燃气轮机、1台电制冷机及1台储电、储热和储冷设备。各设备相关参数如表 1所示。
表 1
设备参数
| 参数 | 数值 |
| 燃气锅炉最大/最小产热功率/MW | 80/0 |
| 燃气锅炉产热功率爬升上、下限/(MW/h) | 25/−25 |
| 燃气锅炉转化效率 | 0.92 |
| P2G甲烷化效率 | 0.7 |
| P2G最大/最小耗电功率/MW | 120/0 |
| CCS最大运行工况能耗/MW | 150 |
| CCS富液存储设备最大/最小容量/m3 | 29 200/0 |
| CCS贫液存储设备最大/最小容量/m3 | 29 200/0 |
| CCS富、贫液存储设备初始容量/m3 | 14 600/14 600 |
| 燃煤机组最大/最小发电功率/MW | 162/45 |
| 燃煤机组输出功率爬升上、下限/(MW/h) | 100/−100 |
| 电加热锅炉最大/最小耗电功率/MW | 40/0 |
| 电加热锅炉用电功率爬升上、下限/(MW/h) | 10/−10 |
| 电加热锅炉电热转化效率 | 0.9 |
| 燃气轮机最大/最小发电功率/MW | 350/0 |
| 燃气轮机最大/最小产热功率/MW | 300/0 |
| 燃气轮机功率爬升上、下限/(MW/h) | 150/−150 |
| 燃气轮机产热/电效率 | 0.4/0.35 |
| 电制冷机最大/最小耗电功率/MW | 40/0 |
| 电制冷机用电功率爬升上、下限/(MW/h) | 10/−10 |
| 电制冷机电冷转化效率 | 0.9 |
| 储热储冷设备容量上、下限/(MW/h) | 120/20 |
| 储热储冷设备最大充、放电功率/MW | 15/15 |
| 储热储冷设备充、放电效率 | 0.95/0.95 |
| 储热储冷设备自损失系数 | 0.01 |
| 储热储冷设备初始容量/(MW/h) | 60 |
| 储电设备容量上、下限/(MW/h) | 60/10 |
| 储电设备最大充、放电功率/MW | 5/5 |
| 储电设备充、放效率 | 0.9/0.9 |
| 储电设备自放电系数 | 0.001 |
| 储电设备初始容量/(MW/h) | 30 |
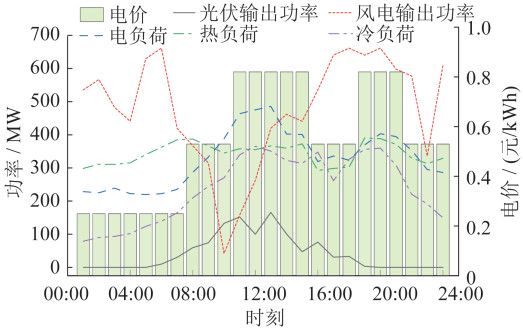
本文仿真中光伏和风电输出功率、负荷预测及分时电价如图 3所示。
本文利用MATLAB中yalmip工具箱和商业求解器CPLEX对该线性规划模型进行求解。
4.2 日前调度不同负荷参与下的调度结果分析
为验证本文调度策略的有效性及需求侧响应对调度结果的影响,设置以下4种场景进行对比分析:场景1,3种柔性负荷均参与调控;场景2,仅电负荷参与调控;场景3,仅热负荷参与调控;场景4,仅冷负荷参与调控。
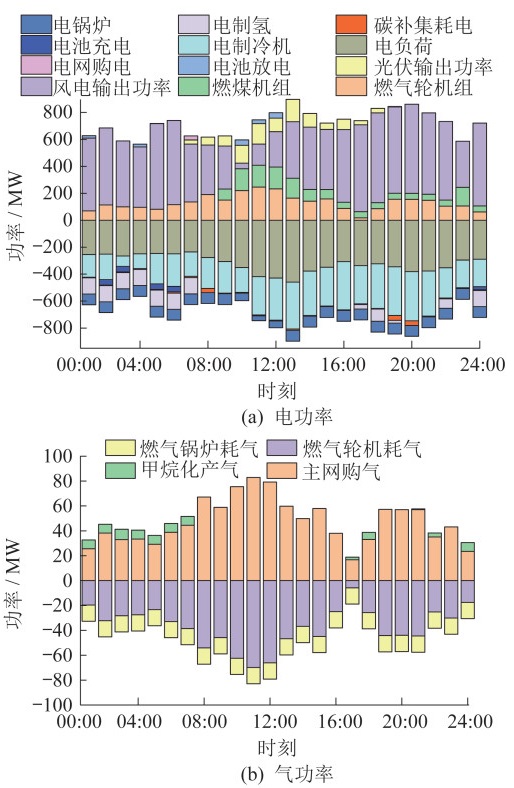
场景1下电、气功率平衡情况如图 4所示。
供电资源有光伏、风机、燃气轮机、燃煤机组、储能放电及电网供电。其中,光伏和风机由于存在弃风、弃光惩罚成本,优先使用。燃气轮机机组24 h供电量多于燃煤机组,这是因为燃煤机组的运维成本和碳排放成本大于燃气轮机机组的用气成本。
P2G、电锅炉用电及甲烷化产气集中在01:00—07:00时段。这是由于这段时间内电价便宜,P2G及电锅炉用电成本低。由于CCS可以从多方面获得CO2,因此耗电量较少。为进一步降低成本,蓄电池在电价低时充电,电价高时放电。
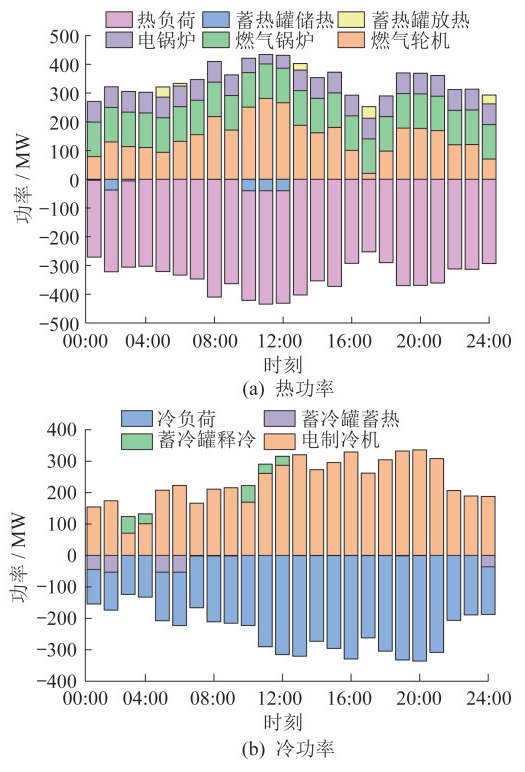
场景1下冷、热功率平衡情况如图 5所示。
供热资源包括电锅炉供热、燃气锅炉供热、燃气轮机供热及储热罐放热。供热主要由燃气轮机及燃气锅炉供给,电锅炉在电价较低时购热。燃气轮机供热大于燃气锅炉供热。这是由于燃气轮机碳排放少于燃气锅炉碳排放,使得碳交易成本较低。
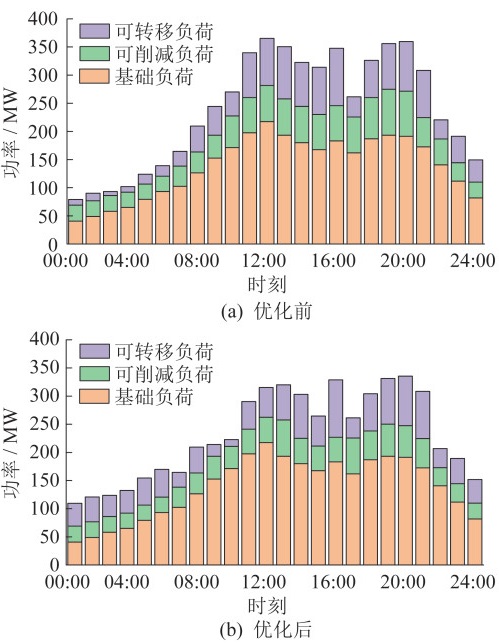
以冷负荷需求侧响应为例验证本文模型的有效性。冷负荷优化前后对比如图 6所示。
由图 6可知,冷负荷将11:00—15:00,19:00 —21:00时段的部分负荷转移到01:00—07:00时段。这是因为电制冷机需要用电,而电价在11:00—15:00和19:00—21:00时段较高,在01:00—07:00时段较低。
场景2、3、4的各功率平衡与场景1类似,此处不再赘述。4种场景下不同负荷参与调控的成本对比如表 2所示。
表 2
4种场景下不同负荷参与调控的成本对比
| 场景 | 转移负荷总量/MW | 削减负荷总量/MW | 总成本/万元 |
| 1 | 556.99 | 550.28 | 496.50 |
| 2 | 162.50 | 181.11 | 502.20 |
| 3 | 185.85 | 196.25 | 500.96 |
| 4 | 197.24 | 175.57 | 503.57 |
由表 2可以看出,场景1的经济性最好。这是因为冷、热、电3种负荷同时参与调度,彼此耦合下可调整空间较大,所以经济性最好。
4.3 日前调度下CCS-P2G耦合模型调度结果分析
为验证本文模型的经济性及CCS-P2G耦合模型的有效性,设置以下4种场景进行成本对比:场景1,CCS+P2G;场景2,不考虑CCS和P2G耦合;场景3,仅考虑P2G,碳直接排放到大气中;场景4,仅考虑CCS。4种场景成本对比如表 3所示。
表 3
4种场景成本对比
| 场景 | 碳交易成本 | 碳封存成本 | 燃煤机组成本 | 弃风弃光成本 | 购气成本 | 购电成本 | 总成本 |
| 1 | 14.04 | 0 | 37.51 | 3.81 | 397.12 | 0.75 | 453.23 |
| 2 | 46.28 | 0.12 | 56.49 | 3.92 | 412.59 | 0.03 | 518.43 |
| 3 | 59.99 | 0 | 45.23 | 3.85 | 454.43 | 9.09 | 572.59 |
| 4 | 46.27 | 0 | 55.48 | 3.93 | 411.13 | 0.02 | 516.83 |
由表 3可知,场景1的总成本比其他场景总成本低。从碳交易成本看,场景1通过碳捕集,将CO2封存或者通过甲烷化转化为天然气降低碳排放量,因此碳交易成本较低;从购气成本看,由于场景1可以实现P2G及碳转气,选择余地大,因此成本较低。由于场景2 CCS和P2G不存在耦合,因此CO2只能通过封存或者排放到大气中去,使得碳排放成本变高。由于天然气只能从气网或者P2G中获得,因此购气成本变高,总成本也变高。由于场景3、场景4仅考虑了P2G、CCS的单一功能,因此CO2排放到大气中的比例较大,碳交易成本、购气成本变高。此外,为了保证天然气供应,通过P2G所需电量也会增大,因此购电成本变高。综上所述,无论是从经济性还是环境友好角度考虑,CCS和P2G耦合均优于其他场景。
4.4 多时间尺度优化结果分析
多时间尺度优化调度结果对比如表 4所示。
表 4
多时间尺度优化调度结果对比
| 优化调度结果 | 日前 | 日内 | 实时 |
| 日运行成本/万元 | 452.77 | 457.34 | 461.62 |
| 风电消纳量/MW | 11 420.34 | 11 572.50 | 11 659.80 |
| 光伏消纳量/MW | 1 007.10 | 1 132.50 | 1 126.20 |
| 风电消纳率/% | 97.70 | 98.90 | 99.70 |
| 光伏消纳率/% | 98.10 | 99.30 | 98.80 |
由表 4可知,实时调度成本最高,日前调度结果成本最低,但这并不代表日前调度策略最优。因为日前调度提前1 d按照风电、光伏的预测值进行计算,未考虑风电、光伏不确定性对调度结果的影响,不能反应系统实际运行的真实状况。多时间尺度优化通过缩短预测范围来减小预测误差,得出的结果更具可靠性。实时优化调度在得到日前、日内部分调度结果的基础上,提前1 h预测风电、光伏输出功率,使预测结果更加准确,优化调度有效性更好。
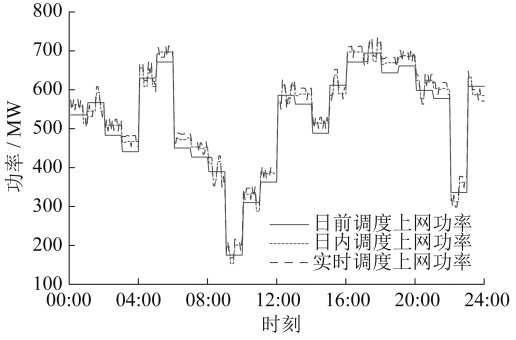
多时间尺度可再生能源上网功率对比如图 7所示。
由图 7可知,多时间尺度优化能够提升新能源的消纳效果,日内调度下风电的消纳率有所提高。这表明多时间尺度调度对于维持系统实际稳定运行,提高新能源消纳效果明显。
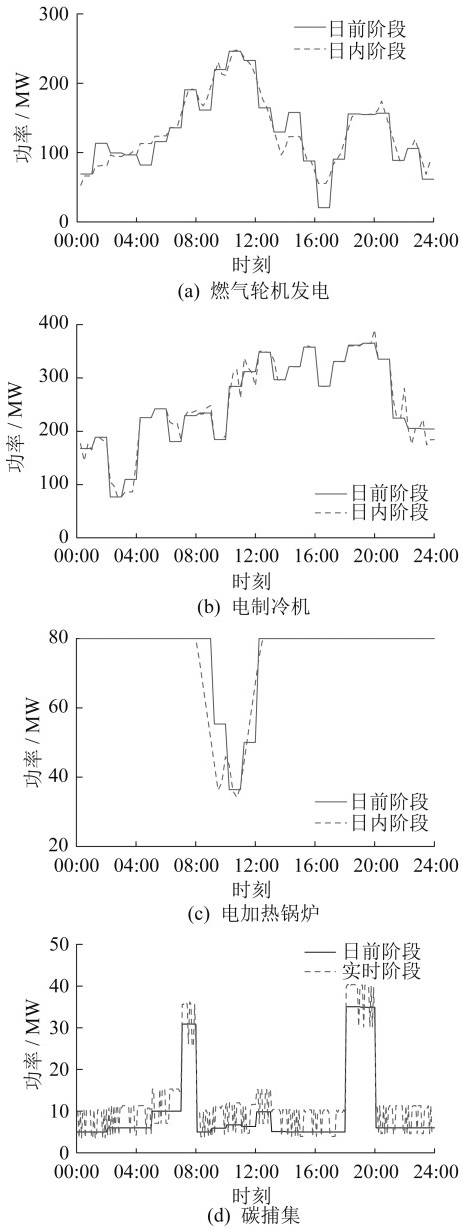
多时间尺度部分机组输出功率如图 8所示。
由图 8可知,在日内阶段,由于考虑了风光输出功率的不确定性,因此能更精确地描述不确定变量的预测误差,使机组输出功率结果更符合实际。由图 8(a)~(c)可知,各机组运行状态与日前调度阶段符合,且考虑了不确定后,日内调度阶段能通过灵活调节各能源设备的输出功率,实现日内低碳经济运行。由图 8(d)可知,通过碳捕集能耗的实时调整,能够及时快速应对实时阶段发生的风电、光伏输出功率短时间变化情况,提高实时调度风电消纳和功率波动平抑。
5 结论
本文提出了一种基于P2G-CCS耦合的考虑需求侧响应的多时间尺度优化调度策略,建立了P2G-CCS耦合模型、需求响应模型以及多时间尺度优化调度模型。通过算例分析可得如下结论。
(1)在日前阶段,电能、冷能、热能需求侧资源共同参与调度,能够进一步挖掘IES的调度潜力,实现源侧与荷侧的深度融合。阶梯碳交易机制融入了阶梯价格及补偿系数,与CCS系统结合后,在约束碳排放同时带来了可观的经济效益。
(2)P2G-CCS耦合模型在提升新能源消纳、减少碳排放量方面具有显著优势。通过CCS将捕集到的CO2提供给P2G生成天然气,降低了IES系统的碳排放量,提高了新能源的消纳率。
(3)多时间尺度优化能够应对风光出力的不确定性,建立的日前-日内-实时模型在消纳新能源、减少碳排放量以及提高经济性上都有显著效果。
参考文献
-
[1]孙大陆. "双碳"背景下中国天然气发电战略思考及中国海油实践[J]. 中国海上油气, 2023, 35(5): 232-242.
-
[2]李欣, 李涵文, 陈德秋, 等. 储液式CCS耦合P2G的综合能源系统低碳经济调度[J/OL]. 电力系统及其自动化学报: 1-8[2024-04-16]. https://10.19635/j.cnki.csu-epsa.001301.
-
[3]陈登勇, 刘方, 刘帅. 基于阶梯碳交易的含P2G-CCS耦合和燃气掺氢的虚拟电厂优化调度[J]. 电网技术, 2022, 46(6): 2042-2054.
-
[4]吴静, 德格吉日夫, 谭忠富, 等. 计及P2G与CCHP技术的综合能源系统多目标协同优化模型[J]. 电测与仪表, 2021, 58(5): 20-30.
-
[5]王义军, 李梦涵, 齐岩. 计及碳捕集电厂综合灵活运行方式的含P2G综合能源系统低碳经济调度[J]. 电力自动化设备, 2023, 43(1): 1-8.
-
[6]程韧俐, 李江南, 周保荣, 等. 含碳捕集-电转气的风光火储一体化系统优化运行[J/OL]. 上海交通大学学报: 1-21[2024-04-16]. https://10.16183/j.cnki.jsjtu.2022.270.
-
[7]王守文, 李国祥, 闫文文, 等. 计及改进生物质燃气和阶梯碳交易的综合能源系统低碳经济调度[J]. 电力系统及其自动化学报, 2024, 36(2): 126-134.
-
[8]胡福年, 周小博, 张彭成, 等. 计及碳捕集的综合能源系统低碳经济优化调度[J]. 太阳能学报, 2024, 45(3): 419-427.
-
[9]宋晓通, 李文博, 周京华, 等. 碳交易机制下计及P2G及负荷柔性特征的低碳经济调度[J/OL]. 电测与仪表: 1-11[2024-04-16]. https://h-p.kns.cnki.net/kcms/detail/23.1202.TH.20221021.1503.016.html.
-
[10]徐艳芳, 杨培宏, 赵欢, 等. 电热综合能源系统多时间尺度优化调度策略研究[J]. 电工技术, 2023(20): 41-44.
-
[11]柴园园, 赵晓波, 吕超贤, 等. 基于Fisher时段划分的配电网源-网-荷-储多时间尺度协调优化调控策略[J]. 电网技术, 2024, 48(4): 1593-1606.
-
[12]李强, 王璇, 琚诚, 等. 基于广义储能的多时间尺度综合能源系统优化调度模型[J/OL]. 南方电网技术: 1-10[2024-04-17]. https://h-p.kns.cnki.net/kcms/detail/44.1643.TK.20231120.1054.002.html.
-
[13]李天格, 胡志坚, 陈志, 等. 计及电-气-热-氢需求响应的综合能源系统多时间尺度低碳运行优化策略[J]. 电力自动化设备, 2023, 43(1): 16-24.
-
[14]林旗斌. 基于模型预测控制的含压缩空气储能微能网多时间尺度优化调度方法[J]. 电气技术, 2023, 24(7): 11-19.
-
[15]王辉, 周珂锐, 吴作辉, 等. 含电转气和碳捕集耦合的综合能源系统多时间尺度优化调度[J/OL]. 中国电力: 1-13[2024-04-18]. https://h-p.kns.cnki.net/kcms/detail/11.3265.TM.20240308.1431.002.html.