发布时间: 2024-10-28
摘要点击次数:
全文下载次数:
DOI: 10.3969/j.issn.2096-8299.2024.05.002
2024 | Volume 40 | Number 5

特约专栏：电力系统先进控制技术

时变时滞多区域互联电力系统滑模负荷频率控制方法

肖雄英, 杨帆

上海电力大学电气工程学院, 上海 200090

收稿日期: 2024-02-22

基金项目: 国家自然科学基金(52377111)

中图法分类号: TM315

文献标识码: A

文章编号: 2096-8299(2024)05-0397-08

摘要

开放式通信网络在互联电力系统中的普遍使用，使原来专用通道的恒定时滞变成了时变时滞。时变时滞恶化了负荷频率控制（LFC）的动态性能，导致系统频率不稳定，因此提出了一种用于时变时滞多区域互联电力系统的滑模LFC方法，并基于Lyapunov泛函进行了稳定性分析。首先，Caputo型分数阶Lyapunov泛函被引入到稳定性分析，通过调整函数积分的上限，减少了稳定性分析的保守性；然后，结合Lyapunov理论和积分不等式，得到线性矩阵不等式描述的时变时滞电力系统的稳定性条件；最后，通过仿真，验证了所提出的控制策略对LFC动态性能的影响，及对负载扰动和风机功率波动的鲁棒性。

关键词

分数阶Lyapunov泛函; 互联电力系统; 负载频率控制; 稳定性分析; 时变时滞

Sliding Mode Load Frequency Control for Interconnected Power Systems with Time-Varying Delayed Multi-Regions

XIAO Xiongying, YANG Fan

School of Electrical Engineering, Shanghai University of Electric Power, Shanghai 200090, China

Abstract

The common use of open communication networks in interconnected power systems has turned the constant time delay of the original dedicated channel into the time-varying time delay. The time-varying time delay deteriorates the dynamic performance of load frequency control(LFC)and lead to system frequency instability. Therefore, the sliding mode LFC method for time-varying delayed multi-regions interconnected power systems is proposed and stability analysis is conducted based on the Lyapunov functionals. Firstly, the Caputo-type fractional-order Lyapunov functional is introduced into the stability analysis, and the conservativeness of the stability analysis is reduced by adjusting the upper limit of the function integral; then, the stability conditions of the time varying time delay power system described by the linear matrix inequality are obtained by combining Lyapunov theory and the integral inequality; finally, simulations are conducted to verify the impact of the proposed control strategy on the dynamic performance of the LFC and the robustness to load disturbances and wind power fluctuations.

Key words

fractional-order Lyapunov functional; interconnected power system; load frequency control; stability analysis; time-varying time delay

负荷频率控制（Load Frequency Control，LFC）在维持电力系统的安全和稳定运行方面发挥着重要作用^[1]。大规模、广域的电力系统通常使用开放式通信网络进行信息传输^[2]。这种类型的通信网络允许大规模和高容量的信息交流，因此提供了从全球角度分析和控制电力系统的可能性^[3]。但是网络传输的信息不可避免地存在通信引起的时滞，这些时滞会影响大多数LFC方案^[4]的实施，因此设计时需要考虑时滞^[5]。文献[6]提出了变论域模糊比例积分（Proportional Integral，PI）的LFC策略，能更好地处理风电出力不确定性对互联电力系统频率稳定的影响。文献[7]分析了一个使用时滞相关方法的LFC方案。文献[8]基于线性矩阵不等式的优化，提出了一种针对通信网络中具有不确定参数和时滞的电力系统鲁棒性LFC方案。文献[9]提出在LFC方案中加入延迟抵消项来解决时滞问题。然而，当使用独立的通信系统进行信息交换时传输信息的时滞是显著和随机的。因此，对于时变时滞电力系统LFC的研究主要集中在稳定性分析和控制器的设计上。

系统稳定性分析分为频域和时域方法，其中频域方法只能处理恒定时滞^[10]，时变时滞系统的稳定性分析大多采用时域方法。文献[11]分析了多区域时滞电力系统的稳定性，文献[12]研究了时变时滞对单区域LFC的影响，文献[13]分析了多机电力系统LFC时滞的稳定性，文献[14]研究了时变时滞对不同PI控制器参数LFC的影响。文献[15]在开发了一个积分不等式后，基于反凸不等式研究了时滞对具有非线性扰动LFC的影响。文献[16]基于二阶Bessel-Legendre积分不等式，讨论了时滞对具有不同增量Lyapunov函数非线性扰动的LFC影响。文献[17]使用了一个基于Wirtinger积分不等式及其仿射的版本，但由于其整数阶参数的限制使其函数结构不能灵活改变，导致上述积分不等式不能有效降低多区互连时滞系统稳定性分析的保守性。另外，控制器的设计要满足特定的时滞要求，使系统能够保证一定的运行性能。文献[18]中，通信时滞被表示为系统的乘法不确定性，并通过仿真验证了该控制器对时滞的抑制作用。上述方法都是基于Padé变换的方法，但这种方法只能处理恒定时滞。对于时变时滞，使用改进的预测器可以减少其对系统的不利影响，提高系统的性能^[19]。文献[20]提出了一种基于直接反馈线性化的离散预测控制方法，可以有效消除通信时滞的影响，保证系统的稳定性。但这些采用状态反馈控制器方法的设计过于保守，影响了控制器的控制效果。文献[21]从控制器的设计条件中得到稳定性条件，然后从滑动模式的表面得出控制器的增益，但没有考虑系统的时滞稳定性，限制了其在实际设计中的应用。

因此，本文提出了一种针对时变时滞多区域互联电力系统稳定性的分析方法。在函数的构造中引入了Caputo型分数阶参数，并采用积分重组的方式降低结果的保守性。通过结合Jensen不等式得到一个新的稳定性准则，优化了计算过程。通过设计考虑时变时滞互联电力系统的滑模控制器，改善系统的动态性能，提高系统在负荷扰动期间的鲁棒性。

1 系统模型

1.1 时变时滞多区域互联电力系统数学模型

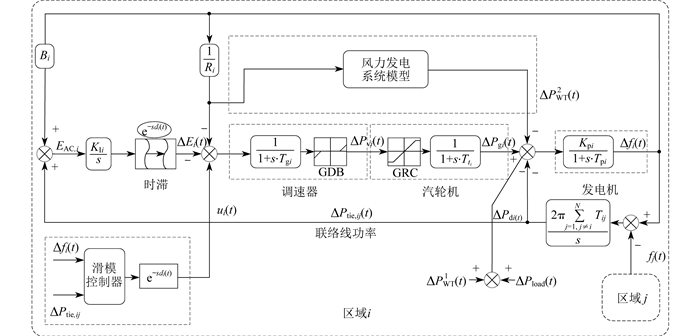
风电参与的时变时滞多区域互联电力系统如图 1所示。其中：i、j分别为区域代码；N为区域总数；ΔP_tie，ij(t)、ΔP_gi(t) 分别为联络线功率偏差、汽轮机功率偏差；ΔP_vi(t) 为调速器阀门位置增益；ΔP_di (t) 为系统总扰动，包括负荷扰动ΔP_load (t) 和风机功率波动ΔP_WT¹ (t)；ΔP_WT² (t) 为与频率变化相关的风机输出功率；GDB、GRC分别为调速器死区模块和发电速率约束模块；u_i (t)为滑膜控制器的控制信号；Δf_i(t)、Δf_j(t) 分别为区域i和区域j的频率偏差；ΔE_i(t) 为区域控制误差的整数偏差；E_{AC, i}为区域i的控制误差；T_ij为第i区域与第j区域的互连增益；T_pi、K_pi分别为电力系统时间常数和增益常数；T_ti为汽轮机时间常数；T_gi、R_i分别为调速器时间常数和调速参数；d_i(t)为第i区域的时变时滞；K_Ii为积分控制增益；B_i为频率偏差系数。

图 1 时变时滞多区域互联电力系统

区域i的互联电力系统模型的动态公式可以表示为

$ \Delta \dot{P}_{\text {tie }, i j}(t)=2 {\rm{ \mathsf{ π}}} \sum\limits_{j=1, j \neq i}^N T_{i j}\left[\Delta f_i(t)-\Delta f_j(t)\right] $

(1)

$ \Delta \dot{f_i}(t)=-\frac{1}{T_{\mathrm{p} i}} \Delta f_i(t)+\frac{K_{\mathrm{p} i}}{T_{\mathrm{p} i}}\left[\Delta P_{\mathrm{g} i}(t)-\Delta P_{\mathrm{d} i}(t)-\Delta P_{\mathrm{tie}, i j}(t)\right] $

(2)

$ \Delta \dot{P}_{\mathrm{g} i}(t) =-\frac{1}{T_{\mathrm{t}i}} \Delta P_{\mathrm{g} i}(t)+\frac{1}{T_{\mathrm{t} i}} \Delta P_{\mathrm{v} i}(t) $

(3)

$ \Delta \dot{E}_i(t) =K_{\mathrm{I} i}\left[B_i \Delta f_i(t)+\Delta P_{\mathrm{tie}, i j}(t)\right] $

(4)

$ \begin{aligned} \Delta \dot{P}_{\mathrm{v} i}(t)= & -\frac{1}{T_{\mathrm{g} i}} \Delta P_{\mathrm{v} i}(t)-\frac{1}{R_i T_{\mathrm{g} i}} \Delta f_i(t)+\frac{1}{T_{\mathrm{g} i}} u_i(t)- \\ & \frac{1}{T_{\mathrm{g} i}} \Delta E_i\left[t-d_i(t)\right] \end{aligned} $

(5)

1.2 风电机组数学模型

风力发电机类型主要包括异步发电机和同步发电机。其中，异步发电机又分为鼠笼式感应发电机（Squirrel Cage Induction Generator，SCIG）和双馈感应发电机（Doubly Fed Induction Generator，DFIG）。由于SCIG具有造价低、结构简单等特性，使其在工程中被广泛应用。但SCIG存在转速不可控和功耗大等问题，不利于其在LFC中应用。DFIG凭借其高可靠性和良好的有功、无功功率独立调节能力等优点，成为风能开发中的主要发电机型^[22]，同时也作为LFC研究中常用的机型。

对于参与调频的风电机组，本文一方面考虑了风速v、风机叶片半径r和桨距角β等参数变化导致的风机功率波动，另一方面用线性化的数学模型来表征其动态特征^[23]。

风能利用率C_p的公式为

$ C_{\mathrm{p}}(\lambda, \beta)=0.22\left(\frac{116}{\lambda_i}-0.4 \beta-5\right) \mathrm{e}^{-\frac{12.5}{\lambda_i}} $

(6)

$ \lambda_i=1 /\left[\frac{1}{\lambda+0.08 \beta}-\right. \left.\frac{0.035}{\beta^3+1}\right] $

(7)

$ \lambda =\omega \frac{r}{v} $

(8)

式中：λ——叶尖速比。

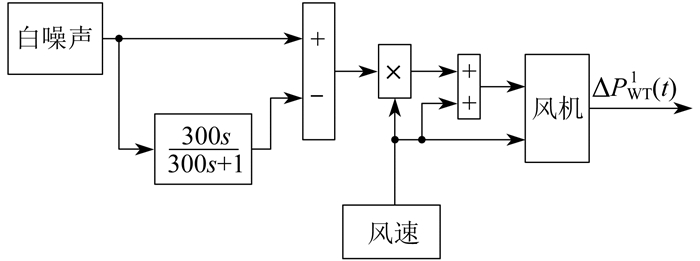
在对风机功率波动进行建模时，风速是主要影响因素。为了模拟风速的随机波动，在数学模型中引入了白噪声模块^[24]。风机功率波动模型如图 2所示。

图 2 风机功率波动模型

线性化风力发电系统模型如图 3所示。K_PWi、K_PWj分别为风力发电系统的增益系数；T_PWi、T_PWj分别为风力发电系统的时间常数；ΔX_ai、ΔX_bi分别为风力发电系统的状态变量。

图 3 风力发电系统模型

本文采用了由液压变桨距执行器、数据拟合桨距角响应和叶片特性3个部分组成的传递函数，其公式为

$ \begin{equation*} G(s)=\frac{1}{T_{\mathrm{PW}j} s+1} \cdot \frac{K_{\mathrm{PW} i} T_{\mathrm{PW} i} s+K_{\mathrm{PW} i}}{s+1} \cdot \frac{K_{\mathrm{PW} j}}{s+1} \end{equation*} $

(9)

而不参与调频的风电机组是非线性的，其非线性模型的动态方程如下：

$ P_{\mathrm{WT}}=C_{\mathrm{p}} \frac{1}{2} \rho A \frac{r^{3}}{\lambda^{3}} v^{2} \omega $

(10)

$ T_{\text {turb }}=C_{\mathrm{p}} \frac{1}{2} \rho A \frac{r^{3}}{\lambda^{3}} v^{2} $

(11)

式中：P_WT——风电机组输出功率；

ρ——空气密度；

A——风机叶片扫过面积；

ω——风机角速度；

T_turb——风力涡轮机机械转矩。

1.3 系统状态方程

选择用于构成状态方程的状态向量x_i(t) ∈ R^N，表示为

$ \begin{align*} & \boldsymbol{x}_{i}(t)=\left[\Delta P_{\mathrm{tie}, i j}(t) \quad \Delta f_{i}(t) \quad \Delta P_{\mathrm{g} i}(t) \quad \Delta E_{i}(t)\right. \\ &\;\; \;\; \;\; \;\;\left.\Delta P_{\mathrm{v} i}(t) \quad \Delta P_{\text {wind }}(t) \quad \Delta X_{\mathrm{a} i} \quad \Delta X_{\mathrm{b} i}\right]^{\mathrm{T}} \end{align*} $

(12)

其中：

$ \begin{gather*} \Delta \dot{P}_{\mathrm{wind}}(t)=-\Delta P_{\mathrm{wind}}(t)+K_{\mathrm{PW} j} \Delta X_{\mathrm{a} i} \end{gather*} $

(13)

$ \Delta \dot{X}_{\mathrm{a} i}=\frac{K_{\mathrm{PW}_{i}} T_{\mathrm{PW}{i}}}{T_{\mathrm{PW} j}} \Delta f_{i}(t)-\Delta X_{\mathrm{a} i}+\left(K_{\mathrm{PW}{i}}-\frac{K_{\mathrm{PW}{i}} T_{\mathrm{PW}_{i}}}{T_{\mathrm{PW} j}}\right) \Delta X_{\mathrm{b} i} $

(14)

$ \begin{equation*} \Delta \dot{X}_{b i}=-\frac{1}{T_{\mathrm{PW} j}} \Delta X_{\mathrm{b} i}+\frac{1}{T_{\mathrm{PW} j}} \Delta f_{i}(t) \end{equation*} $

(15)

考虑时变时滞和风力发电系统的频率调节，多区域互联电力系统第i区域的状态方程为

$ \begin{align*} & \dot{\boldsymbol{x}}_{i}(t)= \boldsymbol{A}_{i} \boldsymbol{x}_{i}(t)+\boldsymbol{B}_{i} \boldsymbol{u}_{i}(t)+\boldsymbol{A}_{\mathrm{id} i} \boldsymbol{x}_{i}\left[t-d_{i}(t)\right]+\boldsymbol{F}_{i} \Delta P_{\mathrm{d} i}(t)+ \\ & \;\;\;\;\sum\limits_{j=1, j \neq i}^{N} \boldsymbol{E}_{i j} \boldsymbol{x}_{j}(t) \end{align*} $

(16)

其中：

$ A_i=\left[\begin{array}{cccccccc} 0 & 2 {\rm{ \mathsf{ π}}} \sum\limits_{j=1, j i j}^N T_{i j} & 0 & 0 & 0 & 0 & 0 & 0 \\ -\frac{K_{\mathrm{p} i}}{T_{\mathrm{p} i}} & -\frac{1}{T_{\mathrm{p} i}} & \frac{K_{\mathrm{p} i}}{T_{\mathrm{p} i}} & 0 & 0 & -\frac{K_{\mathrm{p} i}}{T_{\mathrm{p} i}} & 0 & 0 \\ 0 & 0 & -\frac{1}{T_{\mathrm{t} i}} & 0 & \frac{1}{T_{\mathrm{t}i}} & 0 & 0 & 0 \\ (-1)^{i+1} K_{\mathrm{I} i} & K_{\mathrm{I} i} B_i & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & -\frac{1}{R_i T_{\mathrm{g} i}} & 0 & 0 & -\frac{1}{T_{\mathrm{g} i}} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & -1 & K_{\mathrm{PW} j} & 0 \\ 0 & \frac{K_{\mathrm{PW} i} T_{\mathrm{PW} i}}{T_{\mathrm{PW} j}} & 0 & 0 & 0 & 0 & -1 & K_{\mathrm{PW}_i}-\frac{K_{\mathrm{PW}} T_{\mathrm{PW} i}}{T_{\mathrm{PW} j}} \\ 0 & \frac{1}{T_{\mathrm{PW} j}} & 0 & 0 & 0 & 0 & 0 & -\frac{1}{T_{\mathrm{PW} j}} \end{array}\right] $

(17)

$ \boldsymbol{A}_{\mathrm{id}i}=\left[\begin{array}{cccccccc} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & -\frac{1}{T_{\mathrm{g} i}} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{array}\right] $

(18)

$ \boldsymbol{E}_{i j}=\left[\begin{array}{cccccccc} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & \frac{K_{\mathrm{p} i}}{2 {\rm{ \mathsf{ π}}} T_{\mathrm{p} i}} T_{i j} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & -\frac{K_{\mathrm{I} i}}{2 {\rm{ \mathsf{ π}}}} T_{i j} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{array}\right] $

(19)

$ \boldsymbol{B}_i =\left[\begin{array}{llllllll} 0 & 0 & 0 & 0 & \frac{1}{T_{\mathrm{g} i}} & 0 & 0 & 0 \end{array}\right]^{\mathrm{T}} $

(20)

$ \begin{aligned} \boldsymbol{F}_i =\left[\begin{array}{llllllll} 0 & -\frac{K_{\mathrm{p} i}}{T_{\mathrm{p} i}} & 0 & 0 & 0 & 0 & 0 & 0 \end{array}\right]^{\mathrm{T}} \end{aligned} $

(21)

2 系统稳定性分析及控制器设计

针对风电参与的时变时滞多区域互联电力系统的LFC问题，本文应用分数阶Lyapunov泛函稳定性理论，给出了系统的稳定性条件，再获取系统的滑模控制器设计方法。

2.1 Caputo型分数阶

分数阶微积分是整数阶微积分的延伸，典型的研究有分数阶导数建立的耗散模型、分数阶PID（比例积分微分）控制器模型、分数阶鲁棒控制技术等^[25]。分数阶微积分最常用的定义包括Riemann-Liouville定义（RL定义）、Grunwald-Letnikov定义（GL定义）和Caputo定义。GL和RL分数阶微分方程适合描述初始值处于静止状态的分数阶系统；而Caputo分数阶微分方程适合描述带有非零初始值的实际系统模型，因此更适合实际应用场景。

Caputo定义的分数阶微积分为

$ \begin{equation*} { }_{t_{0}} D_{t}{ }^{\alpha} f(t)=\frac{1}{\Gamma(1-\gamma)} \int_{0}^{t} \frac{f^{(m+1)}(\tau)}{(t-\tau)^{\gamma}} \mathrm{d} \tau \end{equation*} $

(22)

其中，f(t) 是时间变量的多项式，伽玛函数Γ（α）= $ \int_{0}^{\infty} x^{\alpha-1} \mathrm{e}^{-x} \mathrm{~d} x, \alpha=m+\gamma, 0<\gamma \leqslant 1, m \in {{\bf{Z}}}$。

2.2 稳定性分析

定理1 gh给定一组时滞d_i(t)，i= 1，2，3，…，N，满足0 = d₀(t) ≤ d₁(t) ≤ d₂(t) ≤…≤ d_N(t)，如果存在l×l维度对称矩阵P、R_i、Q_i(i = 1，2，3，…，N)，则以下线性矩阵不等式成立：

$ \begin{equation*} \boldsymbol{\varPhi}+\sum\limits_{i=0}^{N-1} \boldsymbol{\varPsi}_{i}<\boldsymbol{O} \end{equation*} $

(23)

其中 P > O，R_i > O，Q_i > O，i= 1，2，3，…，N。Φ、Ψ_i定义在方程式（24）和式（25）中。那么系统式（16）是渐进稳定的。

$ \boldsymbol{\varPhi}=\boldsymbol{c}_{\boldsymbol{i}}^{\mathrm{T}} \boldsymbol{P}_{\mathrm{s}}+\boldsymbol{c}_{\mathrm{s}}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{c}_{i} $

(24)

$ \begin{array}{l} \boldsymbol{\varPsi}_{i}=\left[d_{i+1}(t)-d_{i}(t)\right]^{2} \boldsymbol{c}_{\mathrm{s}}^{\mathrm{T}} \boldsymbol{R}_{i+1} \boldsymbol{c}_{\mathrm{s}}-\left(\boldsymbol{c}_{i+1}-\boldsymbol{c}_{i+2}\right)^{\mathrm{T}} \times \\ \;\;\;\;\;\; \boldsymbol{R}_{i+1}\left(\boldsymbol{c}_{i+1}-\boldsymbol{c}_{i+2}\right)+\boldsymbol{c}_{i+1}^{\mathrm{T}} \boldsymbol{Q}_{i+1} \boldsymbol{c}_{i+1}-\boldsymbol{c}_{i+2}^{\mathrm{T}} \boldsymbol{Q}_{i+1} \boldsymbol{c}_{i+2} \end{array} $

(25)

其中：

$ \begin{array}{l} \boldsymbol{c}_{i}=\left[\begin{array}{lll}\boldsymbol{O}_{l \times(i-1) l} & \boldsymbol{I}_{i \times l} & \boldsymbol{O}_{l \times(N+i-1) l}\end{array}\right],\\ \;\; i=1, 2, 3, \cdots, N, l=2 N+1 \end{array} $

(26)

$ \begin{gather*} \boldsymbol{c}_{\mathrm{s}}=\left[\begin{array}{ll} \boldsymbol{A}_{0} & \boldsymbol{A}_{1} \cdots \boldsymbol{A}_{N} \end{array}\right] \end{gather*} $

(27)

证明选取以下正定Caputo型分数阶Lyapunov泛函：

$ \begin{align*} V(t)= & \boldsymbol{x}^{\mathrm{T}}(t) \boldsymbol{P} \boldsymbol{x}(t)+\sum\limits_{0}^{N-1}\left[d_{i+1}(t)-\right. \\ & \left.d_{i}(t)\right] \int_{-d_{i+1}(t)}^{-d_{i}(t)} \int_{t+\theta+\alpha}^{t} \dot{\boldsymbol{x}}^{\mathrm{T}}(s) \boldsymbol{R}_{i+1} \dot{\boldsymbol{x}}(s) \mathrm{d} s \mathrm{~d} \theta+ \\ & \sum\limits_{i=0}^{N-1} \int_{t-d_{t+1}(t)}^{t-d_{d}(t)} \boldsymbol{x}^{\mathrm{T}}(s) \boldsymbol{Q}_{i+1} \boldsymbol{x}(s) \mathrm{d} s \end{align*} $

(28)

其中，分数阶参数θ=arctan[d_i(t) /d_i+1(t)]。

式（28）为Lyapunov函数引入了一个分数阶参数，通过调整函数积分的上限，减少了稳定性分析的保守性。

式（28）对时间t求导得到

$ \begin{align*} \dot{V}(t)= & 2 \boldsymbol{x}^{\mathrm{T}} \boldsymbol{P} \dot{\boldsymbol{x}}(t)+\sum\limits_{i=0}^{N-1}\left\{\left[d_{i+1}(t)-d_{i}(t)\right]^{2} \dot{\boldsymbol{x}}^{\mathrm{T}}(t+\alpha) \times\right. \\ & R_{i+1} \dot{\boldsymbol{x}}(t+\alpha)-\left[d_{i+1}(t)-d_{i}(t)\right] \times \\ & \left.\int_{t-d_{i+1}(t)}^{t-d_{(t)}} \dot{\boldsymbol{x}}^{\mathrm{T}}(s) R_{i+1} \dot{\boldsymbol{x}}(s) \mathrm{d} s\right\}+ \\ & \sum\limits_{i=0}^{N-1}\left\{\boldsymbol{x}^{\mathrm{T}}\left[t-d_{i}(t)\right] \boldsymbol{Q}_{i+1} \boldsymbol{x}\left[t-d_{i}(t)\right]-\right. \\ & \left.\boldsymbol{x}^{\mathrm{T}}\left[t-d_{i+1}(t)\right] \boldsymbol{Q}_{i+1} \boldsymbol{x}\left[t-d_{i+1}(t)\right]\right\} \end{align*} $

(29)

根据文献[26]中的Jensen积分不等式可得

$ \begin{align*} & -\left[d_{i+1}(t)-d_{i}(t)\right] \int_{t-d_{m+1}(t)}^{t-d_{i}(t)} \dot{\boldsymbol{x}}^{\mathrm{T}}(s) \boldsymbol{R}_{i+1} \dot{\boldsymbol{x}}(s) \mathrm{d} s \leqslant- \\ & {\left[\int_{t-d_{t+1}(t)}^{t-d_{, }(t)} \dot{\boldsymbol{x}}(s) \mathrm{d} s\right]^{\mathrm{T}} \boldsymbol{R}_{i+1}\left[\int_{t-d_{d+1}(t)}^{t-d_{i}(t)} \dot{\boldsymbol{x}}(s) \mathrm{d} s\right]=-\left\{\boldsymbol{x}\left[t-d_{i}(t)\right]-\right.} \\ & \left.\boldsymbol{x}\left[t-d_{i+1}(t)\right]\right\}^{\mathrm{T}} \boldsymbol{R}_{i+1}\left\{\boldsymbol{x}\left[t-d_{i}(t)\right]-\boldsymbol{x}\left[t-d_{i+1}(t)\right]\right\} \end{align*} $

(30)

然后可以推导出

$ \begin{align*} & \dot{V}(t) \leqslant 2 \boldsymbol{x}^{\mathrm{T}} P \dot{\boldsymbol{x}}(t)+\sum\limits_{i=0}^{N-1}\left\{\left[d_{i+1}(t)-d_{i}(t)\right]^{2} \dot{\boldsymbol{x}}^{\mathrm{T}}(t+\alpha) \times\right.\\ & \;\;\boldsymbol{R}_{i+1} \dot{\boldsymbol{x}}(t+\alpha)-\left\{x\left[t-d_{i}(t)\right]-\boldsymbol{x}\left[t-d_{i+1}(t)\right]^{\mathrm{T}}\right\} \times \\ &\;\; \left.\boldsymbol{R}_{i+1}\left\{x\left[t-d_{i}(t)\right]-\boldsymbol{x}\left[t-d_{i+1}(t)\right]\right\}\right\}+ \\ & \;\;\sum\limits_{i=0}^{N-1}\left\{\boldsymbol{x}^{\mathrm{T}}\left[t-d_{i}(t)\right] \boldsymbol{Q}_{i+1} \boldsymbol{x}\left[t-d_{i}(t)\right]-\boldsymbol{x}^{\mathrm{T}}\left[t-d_{i+1}(t)\right] \boldsymbol{Q}_{i+1} \times\right. \\ &\;\; \left.\boldsymbol{x}\left[t-d_{i+1}(t)\right]\right\}=\boldsymbol{\xi}^{\mathrm{T}}(t)\left(\boldsymbol{\varPhi}+\sum\limits_{i=0}^{N-1} \boldsymbol{\varPsi}_{i}\right) \boldsymbol{\xi}(t) \end{align*} $

(31)

即

$ \begin{equation*} \dot{V}(t) \leqslant \xi^{\mathrm{T}}(t)\left(\boldsymbol{\varPhi}+\sum\limits_{i=0}^{N-1} \boldsymbol{\varPsi}_{i}\right) \xi(t) \end{equation*} $

(32)

通过式（32）可知，泛函正定，泛函关于时间导数负定，从而系统式（16）是稳定的。

2.3 控制器设计

对系统式（16）进行如下假设。

假设1 (A_i，B_i) 是完全可控的；时滞项矩阵A_idi是有界的且满足‖A_idi‖ ≤ β_i，其中β_i > 0，i= 1，2，3，…，N；互联矩阵 E_ij和时滞状态向量 x_i [t-d_i(t)] 满足以下条件：‖E_ij‖ ≤ γ_i，‖x_i[t-d_i(t)]‖ ≤ x_max，其中γ_i > 0 x_max=max{ x_i(t)，i=1，2，3，…，N }，‖^*‖是欧氏规范。

当假设1得到满足时，积分型滑模面如下：

$ \begin{equation*} s_{i}(t)=\boldsymbol{G}_{i} \boldsymbol{x}_{i}(t)-\int_{0}^{t} \boldsymbol{G}_{i}\left(\boldsymbol{A}_{i}-\boldsymbol{B}_{i} \boldsymbol{K}_{i}\right) \boldsymbol{x}_{i}(\tau) \mathrm{d} \tau \end{equation*} $

(33)

其中，K_i是通过保证矩阵A_i - B_iK_i的特征值小于零实现的，G_i是满秩的常数矩阵，且G_iB_i是非奇异矩阵。

如果状态轨迹到达滑模面，那么条件s_i(t) = 0就得到满足。因此，通过式（33），可以推导出等效控制律u_ieq (t)为

$ \boldsymbol{u}_{\mathrm{ieq}}(t)=-\boldsymbol{K}_{i} \boldsymbol{x}_{i}(t)-\left(\boldsymbol{G}_{i} \boldsymbol{B}_{i}\right)^{-1} \boldsymbol{G}_{i} \boldsymbol{A}_{\mathrm{id} i} \boldsymbol{x}_{i}\left[t-d_{i}(t)\right] $

(34)

为了确保s_i(t) = 0，还需要设计趋近律，本文使用指数趋近律为

$ \dot{s}_{i}(t)=-a_{1} s_{i}(t)-a_{2} \operatorname{sgn}\left[s_{i}(t)\right], a_{1}>0, a_{2}>0 $

(35)

设Lyapunov函数为

$ \begin{equation*} V_{2}(t)=\sum\limits_{i=0}^{N-1} \frac{1}{2} s_{i}{ }^{2}(t) \end{equation*} $

(36)

对其求导可得到

$ \begin{align*} \dot{V}_{2}(t)= & \sum\limits_{i=0}^{N-1} s_{i}(t) \dot{s}_{i}(t)= \\ & \sum\limits_{i=0}^{N-1} s_{i}(t)\left[\boldsymbol{G}_{i} \dot{\boldsymbol{x}}_{i}(t)-\boldsymbol{G}_{i}\left(\boldsymbol{A}_{i}-\boldsymbol{B}_{i} K_{i}\right) \boldsymbol{x}_{i}(t)\right]= \\ & \sum\limits_{i=0}^{N-1} s_{i}(t)\left\{-a_{1} s_{i}(t)-a_{2} \operatorname{sgn}\left[s_{i}(t)\right]\right\} \leqslant- \\ & \sum\limits_{i=0}^{N-1} s_{i}(t)\left\{\boldsymbol{G}_{i} \varepsilon+a_{1} s_{i}(t)+a_{2} \operatorname{sgn}\left[s_{i}(t)\right]\right\} \leqslant- \\ & \sum\limits_{i=0}^{N-1}\left[a_{1} s_{i}^{2}(t)+a_{2} \frac{s_{i}^{2}(t)}{\left|s_{i}(t)\right|}\right]<0 \end{align*} $

(37)

式中：ε——扰动的上限。

由式（37）可知其导数负定，故满足该趋近律条件。

可以给出最终的控制律为

$ \begin{align*} \boldsymbol{u}_{i}(t)= & -\boldsymbol{K}_{i} \boldsymbol{x}_{i}(t)-\left(\boldsymbol{G}_{i} \boldsymbol{B}_{i}\right)^{-1} \boldsymbol{G}_{i} \boldsymbol{A}_{\mathrm{id} i} \boldsymbol{x}_{i}\left[t-d_{i}(t)\right]- \\ & \left(\boldsymbol{G}_{i} \boldsymbol{B}_{i}\right)^{-1}\left\{s_{i}(t)+\operatorname{sgn}\left[s_{i}(t)\right]\right\} \end{align*} $

(38)

3 仿真结果与分析

利用不同的LFC方案，对图 1所示的时变时滞多区域互联电力系统进行仿真，以验证本文所提的滑膜LFC方法的有效性。建立两区域互联电力系统环境，两区域电力系统和风电机组参数分别如表 1和表 2所示。

表 1 两区域电力系统参数

下载CSV

参数	数值
参数	区域1	区域2
T_pi	10	10
K_pi	1	1
T_ti	0.3	0.25
T_gi	0.08	0.1
R_i	2.5	2.22
B_i	0.425	0.456
T_ij	0.043	0.043
GDB参数/s	0.002 3	0.2
GRC参数/%	0.002 3	0.2

表 2 两区域风电机组参数

下载CSV

区域	P_WT/MW	v/(m/s)	ρ/(kg/m³)	A/m²	r/m	K_PWi	T_PWi
1	3 000	12	1.225	1 648	43.63	1.25	6.000
2	3 000	12	1.225	1 648	43.63	1.40	0.041

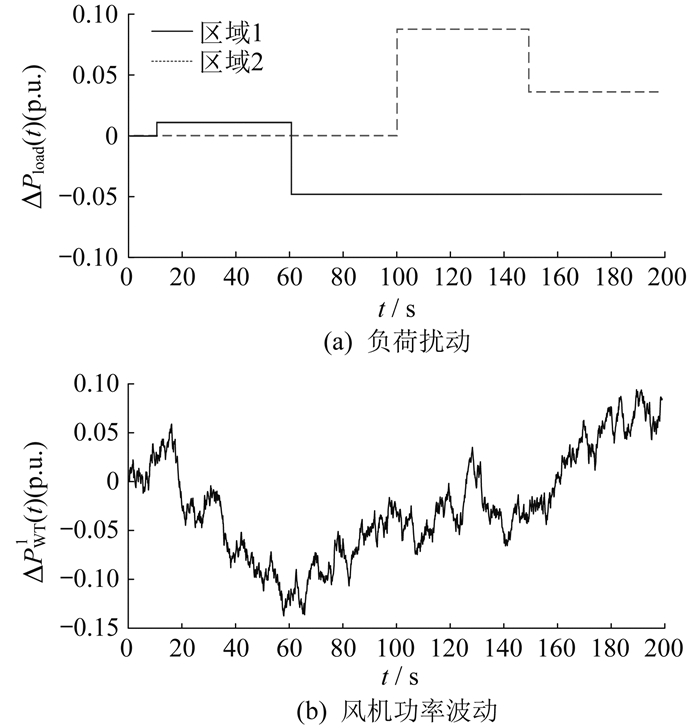
在时变时滞多区域互联电力系统的运行过程中，系统负荷扰动和风机功率波动如图 4所示。

图 4 区域1和区域2的电力系统扰动

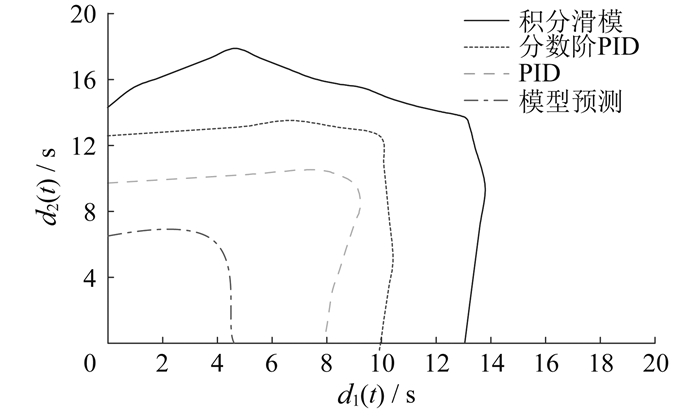
在仿真实验中，将时变时滞当作随机时滞，取两区域时滞分别为d₁(t) = 5sint + 1.8(s)，d₂(t) = 5(s)。在负荷扰动和风机功率波动下，对比本文提出的积分滑膜、分数阶PID^[27]、PID^[4]、模型预测^[28]4种不同LFC方案下的两区域电力系统稳定域，仿真结果如图 5所示。

图 5 不同LFC方案下的两区域电力系统稳定域仿真结果

两区域系统稳定域即为图 5中曲线与坐标轴围成的区域。由图 5可以看出，本文提出的积分滑模LFC方案在提高电力系统时滞稳定域上优于其他3种方案。

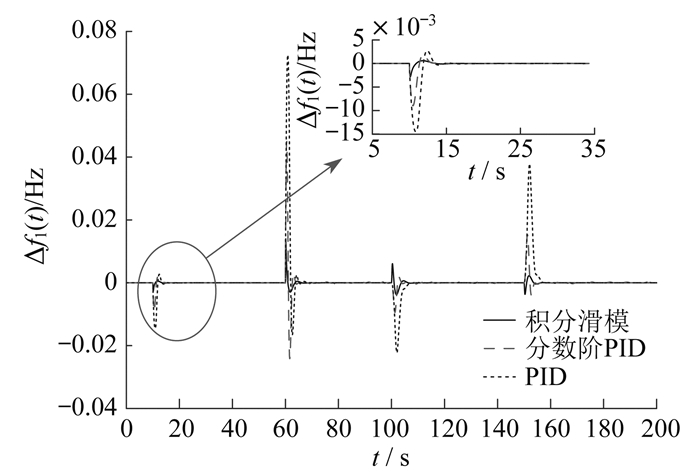
通过总结200 s内的最大频率偏差可以有效地比较不同控制策略的性能。在负荷扰动和风机功率波动下，不同LFC方案的区域1频率偏差对比如图 6所示。

图 6 不同LFC方案的区域1频率偏差对比

由图 6可以看出，本文提出的积分滑模LFC方案可以将最大频率偏差限制在0.02 Hz，并且在含有时变时滞以及负荷扰动和风机功率波动的影响下，该方案对频率偏差也具有很好的抑制作用。

当风电渗透率和时变时滞发生变化时，通过比较200 s内的最大频率偏差，可以验证不同控制策略对系统鲁棒性的影响。d₂（t）=5 s保持不变，改变d₁（t），不同风电渗透率和时变时滞下不同LFC方案的最大频率偏差如表 3所示。

表 3 不同风电渗透率和时变时滞下不同LFC方案的最大频率偏差

下载CSV

风电渗透率/%	d₁(t)/s	最大频率偏差/Hz
风电渗透率/%	d₁(t)/s	积分滑模	分数阶PID	PID
0	0	0.015 8	0.019 7	0.089 5
	3sint + 0.2	0.025 7	0.035 6	0.112 4
	10cost + 1.2	0.036 7	0.045 8	0.126 7
15	0	0.151 4	0.219 1	0.576 0
	3sint + 0.2	0.296 8	0.386 9	1.158 0
	10cost + 1.2	0.425 6	0.561 4	1.568 0
25	0	0.532 5	0.615 8	0.956 4
	3sint + 0.2	0.756 8	0.914 7	1.579 0
	10cost + 1.2	0.806 2	1.091 0	1.969 0

由表 3可以看出，与其他两种LFC方案相比，本文所提的积分滑模LFC方案对时变时滞的鲁棒性最高。因此，该方法能够充分降低风电参与的时变时滞多区域互联电力系统的频率偏差，提高系统的鲁棒性。

4 结语

本文针对风电参与的时变时滞多区域互联电力系统，提出了一种考虑时变时滞的积分滑模LFC方法。通过构建Caputo型分数阶Lyapunov泛函降低了稳定性分析的保守性，然后，结合Lyapunov理论和积分不等式，得到线性矩阵不等式描述的时变时滞多区域互联电力系统的稳定性条件。仿真结果表明，本文所提出的积分滑膜LFC方案在系统稳定域和对频率偏差抑制效果上都体现了优越性，能够确保互联电力系统的快速响应，提高系统在通信时滞影响下的动态性能。

参考文献

[1]

钱伟, 孙晓彤, 费树岷. 可再生能源高渗透下时滞孤岛微电网的负荷频率控制[J]. 电网技术, 2024, 48(2): 630-640.

[2]

SHANGGUAN X C, HE Y, ZHANG C K, et al. Resilient load frequency control of power systems to compensate random time delays and time-delay attacks[J]. IEEE Transactions on Industrial Electronics, 2022, 70(5): 5115-5128.

[3]

TAN G G, SHI Z, LIU P, et al. Robust H_∞ load frequency control of power systems with two time delays[J]. International Transactions on Electrical Energy Systems, 2021, 31(9): e13022.

[4]

GUO R N, XU S Y, GUO J. Sliding-mode synchronization control of complex-valued inertial neural networks with leakage delay and time-varying delays[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2023, 53(2): 1095-1103. DOI:10.1109/TSMC.2022.3193306

[5]

LUO H C, HISKENS I A, HU Z C. Stability analysis of load frequency control systems with sampling and transmission delay[J]. IEEE Transactions on Power Systems, 2020, 35(5): 3603-3615. DOI:10.1109/TPWRS.2020.2980883

[6]

李志军, 王硕, 张家安, 等. 基于变论域模糊逻辑的互联电力系统负荷频率控制[J]. 电力系统保护与控制, 2021, 49(16): 151-160.

[7]

SHEN L, XIAO H Q. Delay-dependent robust stability analysis of power systems with PID controller[J]. Chinese Journal of Electrical Engineering, 2019, 5(2): 79-86. DOI:10.23919/CJEE.2019.000014

[8]

OJAGHI P, RAHMANI M. LMI-based robust predictive load frequency control for power systems with communication delays[J]. IEEE Transactions on Power Systems, 2017, 32(5): 4091-4100. DOI:10.1109/TPWRS.2017.2654453

[9]

YILDIRIM B. Gain and phase margins based stability region analysis of time-delayed shipboard microgrid with sea wave energy[J]. IET Electric Power Applications, 2020, 14(8): 1347-1359. DOI:10.1049/iet-epa.2019.0762

[10]

JIN L, ZHANG C K, HE Y, et al. Delay-dependent stability analysis of multi-area load frequency control with enhanced accuracy and computation efficiency[J]. IEEE Transactions on Power Systems, 2019, 34(5): 3687-3696. DOI:10.1109/TPWRS.2019.2902373

[11]

马静, 李俊臣, 李益楠, 等. 基于改进自由权矩阵与广义特征值的时滞稳定上限计算方法研究[J]. 电力系统保护与控制, 2014, 42(18): 1-8.

[12]

LAI J G, LU X Q, YU X H, et al. Stochastic distributed secondary control for ac microgrids via event-triggered communication[J]. IEEE Transactions on Smart Grid, 2020, 11(4): 2746-2759.

[13]

关琳燕, 周洪, 胡文山. 基于LMI的广域时延多机电力系统的控制与稳定性研究[J]. 电力系统保护与控制, 2016, 44(9): 7-14.

[14]

JIANG L, YAO W, WU Q H, et al. Delay-dependent stability for load frequency control with constant and timevarying delays[J]. IEEE Transactions on Power Systems, 2011, 27(2): 932-941.

[15]

DUAN C, ZHANG C K, JIANG L, et al. Structureexploiting delay-dependent stability analysis applied to power system load frequency control[J]. IEEE Transactions on Power Systems, 2017, 32(6): 4528-4540.

[16]

汪豪, 钱伟, 郭建峰, 等. 变时滞影响下广域电力系统的H_∞控制[J]. 电力系统保护与控制, 2021, 49(18): 70-80.

[17]

钱伟, 蒋鹏冲, 车凯. 基于Wirtinger不等式的时变时滞电力系统稳定性分析[J]. 电力系统保护与控制, 2016, 44(23): 79-85.

[18]

DONG C Y, YANG S F, JIA H J, et al. Padé-based stability analysis for a modular multilevel converter considering the time delay in the digital control system[J]. IEEE Transactions on Industrial Electronics, 2019, 66(7): 5242-5253.

[19]

PATEL U R, MICHIELSSEN E. Wigner-Smith time-delay matrix for electromagnetics: theory and phenomenology[J]. IEEE Transactions on Antennas and Propagation, 2021, 69(2): 902-917.

[20]

XING H T, PLOEG J, NIJMEIJER H. Smith predictor compensating for vehicle actuator delays in cooperative ACC systems[J]. IEEE Transactions on Vehicular Technology, 2019, 68(2): 1106-1115.

[21]

杨旭红, 方浩旭, 贾巍. 基于分数阶滑模控制的直接矩阵变换器控制策略研究[J]. 电力系统保护与控制, 2022, 50(19): 158-166.

[22]

夏越, 张鸿飞, 陈颖, 等. 基于传递函数分析的双馈风力发电系统动态建模方法研究[J/OL]. 中国电机工程学报: 1-15(2023-03-08)[2024-02-20]. http://kns.cnki.net/kcms/detail/11.2107.TM.20230307.1813.009.html.

[23]

GHOLAMREZAIE V, DOZEIN M G, MONSEF H, et al. An optimal frequency control method through a dynamic load frequency control (LFC) model incorporating wind farm[J]. IEEE Systems Journal, 2018, 12(1): 392-401.

[24]

MAGDY G, MOHAMED E A, SHABIB G, et al. SMES based a new PID controller for frequency stability of a real hybrid power system considering high wind power penetration[J]. IET Renewable Power Generation, 2018, 12(11): 1304-1313.

[25]

薛定宇. 分数阶微积分学与分数阶控制[M]. 北京: 科学出版社, 2018: 250.

[26]

GU K, KHARITONOV V L, CHEN J. Stability of timedelay systems[M]. Boston, USA: Birkhäuser, 2003: 322.

[27]

左剑, 王子琪, 李银红, 等. 计及时滞的互联电网负荷频率控制最优分数阶PID控制器设计[J]. 控制理论与应用, 2017, 34(9): 1151-1160.

[28]

张怡, 常鹏飞. 新能源电力系统分布式模型预测负荷频率控制[J]. 电气传动, 2022, 52(20): 70-75.