发布时间: 2024-10-28
摘要点击次数:
全文下载次数:
DOI: 10.3969/j.issn.2096-8299.2024.05.001
2024 | Volume 40 | Number 5

特约专栏：电力系统先进控制技术

基于自适应扰动补偿的有限时间滑模负荷频率控制

李连宝, 杨帆

上海电力大学电气工程学院，上海 200090

收稿日期: 2024-02-25

基金项目: 国家自然科学基金(52377111)

中图法分类号: TM315

文献标识码: A

文章编号: 2096-8299(2024)05-0390-07

摘要

为解决可再生能源输出功率波动性导致的电力系统频率不稳定问题，提出了一种基于自适应扰动补偿的有限时间滑模负荷频率控制（LFC）策略，使得电力系统面对未知扰动时可以在有限时间内实现频率的快速稳定。首先，针对可再生能源输出功率和负荷不确定导致的扰动上界未知问题，引入了一种自适应滑模扰动观测器，在不需要扰动上界信息的情况下获得扰动估计值，并直接在输入通道实现扰动补偿；然后，将自适应滑模扰动观测器与非奇异终端滑模控制（TSMC）相结合，利用终端滑模的有限时间收敛特性实现频率快速稳定。仿真分析发现，所提出的控制策略在面对风光输出功率波动和系统负荷扰动的情况下能快速维持频率稳定，提高了系统调频性能。

关键词

负荷频率控制; 有限时间滑模; 扰动观测器; 自适应策略

Finite Time Sliding Mode Load Frequency Control Based on Adaptive Disturbance Compensation

LI Lianbao, YANG Fan

School of Electrical Engineering, Shanghai University of Electric Power, Shanghai 200090, China

Abstract

Addressing the issue of frequency instability in power systems caused by the fluctuating output of renewable energy sources, the finite-time sliding mode load frequency control (LFC) strategy based on adaptive disturbance compensation is proposed, aiming to achieve rapid and finite-time stability of the system frequency in the presence of unknown disturbances. Firstly, to tackle the challenge of unknown disturbance upper bounds arising from the uncertainty in renewable energy output and load fluctuations, this paper introduces an adaptive sliding mode disturbance observer. This observer, operating without the need for disturbance upper bound information, facilitates the estimation of disturbances and enables direct implementation of disturbance compensation in the input channel. Then, the adaptive sliding mode disturbance observer is integrated with non-singular terminal sliding mode control (TSMC), leveraging the finite-time convergence characteristics of terminal sliding mode to achieve rapid frequency stabilization. Simulation analysis reveals that the proposed control strategy demonstrates its ability to swiftly maintain frequency stability when confronted with fluctuations in wind-solar output and system load disturbances, thereby enhancing the frequency regulation performance of the system.

Key words

load frequency control; finite-time sliding mode control; disturbance observer; adaptive strategy

电力系统频率是电能质量的重要指标之一。负荷频率控制（Load Frequency Control，LFC）负责调整互联电力系统中各个区域发电机组的输出功率，维持发电侧与负荷侧供需平衡，从而确保每个区域的频率稳定^[1-2]。然而，随着可再生能源在电力系统中的渗透率逐步提高，传统的LFC方法难以保证控制效果^[3-4]。一方面，风光等可再生能源受天气等诸多因素的影响，具有强随机性和不确定性，其输出功率频繁波动，系统频率难以维持在标称值附近，控制难度提升；另一方面，可再生能源通过逆变器接入电网，与电网频率解耦，不具备惯量支撑的能力。高比例新能源接入使得电力系统呈现低惯量的特点，系统频率调整能力恶化，面对扰动时更加难以稳定^[5-6]。因此，针对含可再生能源的电力系统设计出先进的LFC策略，从而实现频率的快速稳定是目前研究的重点。

现有的LFC研究成果中，文献[7-9]采用了基于输入-输出反馈的线性控制方法。然而，若考虑非线性环节，如调速器死区（Governor Dead Band，GDB）以及发电机功率约束（Generation Rate Constraint，GRC），则线性方法难以实现良好控制。因此，有必要进一步采用非线性控制方法，例如滑模控制（Sliding Mode Control，SMC）^[10-15]、非线性模型预测控制（Model Predictive Control，MPC）^[16-18]等，以提高控制性能。其中，SMC对扰动和未建模动态具有强鲁棒性，是频率稳定问题的有效解决策略。

在SMC的基础上引入非线性滑模面，可以加速收敛。该方法表现出有限时间收敛的理想特性，被称为终端滑模控制（Terminal Sliding Mode Control，TSMC）^[19-20]。文献[21]将基于神经网络的TSMC用于频率控制。文献[22]将TSMC与人工蜂群优化算法相结合，以实现控制参数最优。然而，上述文献中的奇异性问题没有得到足够的关注。奇异性问题可能导致控制器输出趋近于无穷大，从而使发电机组的输出功率超出安全范围，造成故障或设备损坏。本文在控制回路中采用全阶TSMC，避免对滑模面进行微分，从根本上解决了奇异性问题。

为进一步减少未知扰动所造成的不良影响，在TSMC的基础上加入滑模扰动观测器，实时获得扰动估计值，并直接在输入通道进行扰动补偿，从而实现更为平滑的频率响应。该策略还可避免高扰动估值带来的抖振问题。文献[23-25]所采用的滑模扰动观测器，其设计需要扰动及其导数的精确上界信息，由于可再生能源输出功率的不确定性，该信息却无法获得。本文引入一种自适应策略，在不需要相关扰动信息的情况下实现对未知扰动的估计与补偿，并在计及风光输出功率波动的互联电力系统模型中，对结合自适应扰动补偿与终端滑模的频率控制方案进行了验证。

1 计及风光出力波动的互联电力系统负荷频率控制模型

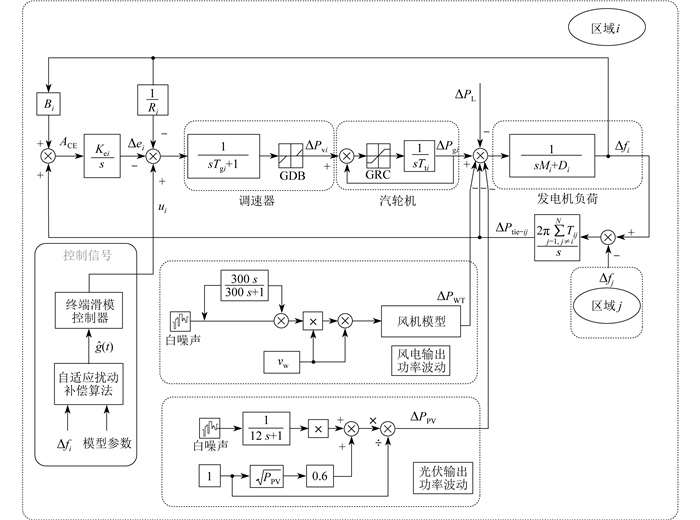
互联电力系统各区域一般选取汽轮机作为主力发电机组。风力发电机组（以下简称“风电机组”）和光伏机组一般采用最大功率跟踪的方式接入电网，不具备调频能力。因此，在负荷频率控制模型中引入风电机组和光伏机组输出功率波动模型，以反映新能源渗透的影响，具体模型如图 1所示。其中，ΔP_tie-ij表示区域i和区域j之间的联络线功率偏差；Δf_i、ΔP_vi、ΔP_gi分别表示区域i频率偏差、汽轮机阀门位置变化量以及汽轮机输出功率变化量；Δe_i为积分控制偏差；u_i为区域i的控制信号；K_ei为积分控制增益，设定为1；ΔP_L为负荷侧扰动；T_ij为区域i和区域j之间的联络线同步系数；N为区域总数；M_i为系统的惯性系数；D_i为负荷阻尼系数；T_ti为汽轮机时间常数；T_gi为调速器时间常数；R_i为调差系数；B_i为频率偏差系数；A_CE为区域控制误差；v_w为风速；ΔP_WT、ΔP_PV分别表示风电机组及光伏机组的输出功率波动；$ \hat g$(t)为集总扰动估计值；t为时间变量；s为拉普拉斯算子；P_PV表示光伏输出功率的初始值。

图 1 互联电力系统负荷频率控制模型

2 基于自适应扰动补偿的有限时间滑模控制策略设计

风电机组和光伏机组输出功率的随机性导致电力系统有功功率不平衡，从而使得频率频繁波动，难以维持稳定。终端滑模控制可以在有限时间内实现频率稳定，避免频率的长期波动；通过自适应扰动观测器实现对未知扰动的补偿，进一步降低由新能源输出功率波动带来的不利影响。

2.1 系统等效状态空间模型的建立

对于区域i的电力系统，用ΔP_sumi表示该区域所受有功功率扰动之和，公式为

$ \Delta P_{\text {sum } i}=\Delta P_{\text {tie- }-i j}+\Delta P_{\mathrm{L}}+\Delta P_{\mathrm{wT}}+\Delta P_{\mathrm{PV}} $

(1)

选取状态变量矩阵x=[x₁，x₂，x₃]=$ \left[\varDelta f_i, \varDelta \dot{f}_i, \varDelta \ddot{f}_i\right]$，状态变量x₁、x₂、x₃分别对应频率偏差及其一阶、二阶导数。对于负荷频率控制模型，频率的一阶、二阶导数存在且可用于控制策略设计^[26]。控制输出系数α、状态变量函数f(x) 和系统扰动d(t) 的公式分别为

$ \alpha=\frac{1}{T_{\mathrm{g} i} T_{\mathrm{t}i} M_i} $

(2)

$ f(\boldsymbol{x})=\boldsymbol{x}\left[\begin{array}{c} -\left(\frac{1}{T_{\mathrm{g} i} T_{\mathrm{t}i} M_i}+\frac{1}{T_{\mathrm{g} i} T_{\mathrm{t}i} M_i R_i}\right) \\ -\left(\frac{1}{T_{\mathrm{g} i} T_{\mathrm{t}i}}+\frac{D_i}{T_{\mathrm{g} i} M_i}+\frac{D_i}{T_{\mathrm{t}i} M_i}\right) \\ -\left(\frac{1}{T_{\mathrm{g} i}}+\frac{1}{T_{\mathrm{t} i}}+\frac{D_i}{M_i}\right) \end{array}\right] $

(3)

$ \begin{aligned} d(t)=& -\frac{1}{T_{\mathrm{g} i} T_{\mathrm{t}i} M_i} \Delta P_{\mathrm{sum}i}-\left(\frac{1}{T_{\mathrm{g} i} M_i}+\frac{1}{T_{\mathrm{t}i} M_i}\right) \Delta \dot{P}_{\mathrm{sum}i}- \\ & \frac{1}{M_i} \Delta \ddot{P}_{\mathrm{sum}i}-\frac{1}{T_{\mathrm{g} i} T_{\mathrm{t} i} M_i} \Delta e_i \end{aligned} $

(4)

考虑系统参数不确定性的影响，等效状态空间模型为

$ \left\{\begin{aligned} & \dot{x}_1=\Delta \dot{f}_i \\ & \dot{x}_2=\Delta \ddot{f}_i \\ & \dot{x}_3=\Delta \dddot{f}_i=f(\boldsymbol{x})+\Delta f(\boldsymbol{x})+(\alpha+\Delta \alpha) u_i+ \\ &\;\;\;\;\;\; d(t)+\Delta d(t)=f(\boldsymbol{x})+\alpha u_i+g(t) \end{aligned}\right. $

(5)

式中：Δf(x)，Δα，Δd(t)——状态变量函数、控制输出系数和系统扰动的变化量；

g(t)——集总扰动，包括参数不确定性和风光输出功率波动等外部扰动的影响。

集总扰动的一阶、二阶导数满足|$ \dot{g}(t)$| < L₁，|$ \ddot g(t)$| < L₂，上界值L₁、L₂均未知。

2.2 自适应扰动补偿

为了获得集总扰动g(t) 的估计值，本文设计了一种有限时间滑模观测器，能够通过输入通道直接进行扰动补偿。

引入辅助变量e，可由变量z表示为

$ e=z-x_{3} $

(6)

变量z的一阶导数为

$ \begin{align*} \dot{z}=& f(\boldsymbol{x})+\alpha u_{i}-c_{1 \mathrm{d}} \operatorname{sgn}(e)|e|^{\alpha_{1 {\rm{d}}}}- \\ & c_{2 \mathrm{d}} \operatorname{sgn}(e) |e|^{\alpha_{2 {\rm{d}}}}+v_{{\rm{z}}} \end{align*} $

(7)

式中：c_1d，c_2d，α_1d，α_2d——常数，c_1d > 0，c_2d > 0，0 < α_1d < 1，α_2d > 1；

v_z——控制输入。

辅助变量e的一阶导数为

$ \begin{align*} \dot{e}=& \dot{z}-\dot{x}_{3}=-c_{1 \mathrm{d}} \operatorname{sgn}(e) | e|^{\alpha_{\mathrm{ld}}}- \\ & c_{2 \mathrm{d}} \operatorname{sgn}(e)|e|^{\alpha_{2 \mathrm{d}}}+v_{\mathrm{z}}-g(t) \end{align*} $

(8)

将观测器滑模面σ_d设计为

$ \begin{equation*} \sigma_{\mathrm{d}}=\dot{e}+c_{1 \mathrm{d}} \operatorname{sgn}(e)|e|^{\alpha_{1 \mathrm{d}}}+c_{2 \mathrm{d}} \operatorname{sgn}(e)|e|^{\alpha_{2 {\rm{d}}}} \end{equation*} $

(9)

将式（8）代入到观测器滑模面中可得

$ \begin{equation*} \sigma_{{\rm{d}}}=v_{{\rm{z}}}-g(t) \end{equation*} $

(10)

根据式（10），下一步仅需设计观测器控制输入v_z，使得状态变量抵达观测器滑模面σ_d，此时σ_d趋近于零，可得到集总扰动的估计值。估计值$ {\hat g}$(t) 等于v_z，可应用于控制律的设计以消除扰动带来的不良影响。

定理1 将控制输入v_z设计为

$ \begin{equation*} \dot{v}_{\mathrm{z}}=-\left(\eta_{\mathrm{d}}+k_{\mathrm{d}}\right) \operatorname{sgn}\left(\sigma_{\mathrm{d}}\right), v_{\mathrm{z}}(0)=0 \end{equation*} $

(11)

式中：η_d——正实数项；

k_d——扰动一阶导数上界值。

此时可确保系统状态在有限时间内抵达观测器滑模面σ_d。在抵达滑模面后，扰动估计误差为零，即可完成集总扰动估计。

证明基于式（11），观测器滑模面一阶微分可表示为

$ \begin{equation*} \dot{\sigma}_{\mathrm{d}}=\dot{v}_{\mathrm{z}}-\dot{g}(t)=-\left(\eta_{\mathrm{d}}+k_{\mathrm{d}}\right) \operatorname{sgn}\left(\sigma_{\mathrm{d}}\right)-\dot{g}(t) \end{equation*} $

(12)

选取李雅普诺夫函数V=σ_d² /2，可推得

$ \begin{align*} \dot{V}= & \sigma_{\mathrm{d}} \dot{\sigma}_{\mathrm{d}}=-\eta_{\mathrm{d}}\left|\sigma_{\mathrm{d}}\right|-k_{\mathrm{d}}\left|\sigma_{\mathrm{d}}\right|-\dot{g}(t) \sigma_{\mathrm{d}} \\ & \leqslant\left(|\dot{g}(t)|-k_{\mathrm{d}}\right)\left|\sigma_{\mathrm{d}}\right|-\eta_{\mathrm{d}}\left|\sigma_{\mathrm{d}}\right| \end{align*} $

(13)

由于k_d > L₁ > |$ {\dot g}$(t)|，η_d > 0，可得

$ \begin{equation*} \sigma_{\mathrm{d}} \dot{\sigma}_{\mathrm{d}} \leqslant-\eta_{\mathrm{d}}\left|\sigma_{\mathrm{d}}\right| \end{equation*} $

(14)

因此，所设计的v_z满足要求。

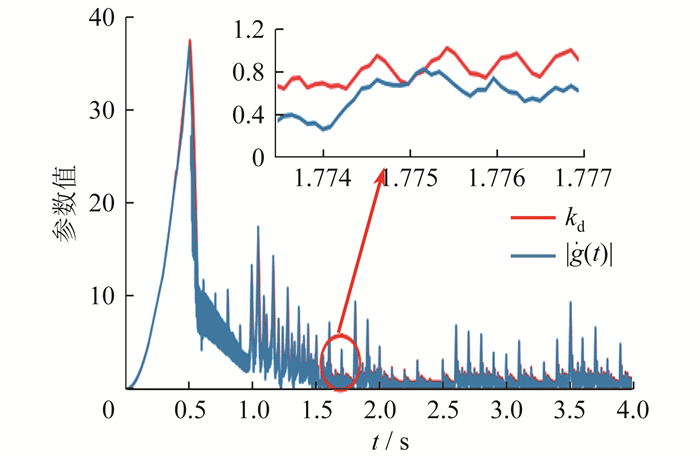
由于风光等新能源输出功率的不确定性，集总扰动一阶导数的上界L₁未知，故无法确定k_d的值。本文引入了自适应策略^[27]，可以自动更新k_d，并在有限时间内实现k_d > | L₁ |，使得观测器的实现过程中无需扰动上限值L₁的相关信息。

引理1 自适应策略中自动更新k_d值的公式

$ \dot{k}_{\mathrm{d}}(t)=-\rho_{\mathrm{d}}(t) \operatorname{sgn}\left[\delta_{\mathrm{d}}(t)\right] $

(15)

$ \dot{r}_{\mathrm{d}}(t)= \begin{cases}\gamma_{\mathrm{d}}\left|\delta_{\mathrm{d}}(t)\right|, & \left|\delta_{\mathrm{d}}(t)\right|>\delta_{0 \mathrm{d}} \\ 0, & \left|\delta_{\mathrm{d}}(t)\right| \leqslant \delta_{0 \mathrm{d}}\end{cases} $

(16)

$ 其中:\quad \quad \rho_{\mathrm{d}}(t)=r_{0 \mathrm{d}}+r_{\mathrm{d}}(t) $

(17)

$ \delta_{\mathrm{d}}(t)=k_{\mathrm{d}}(t)-\frac{1}{\alpha_{\mathrm{d}}}\left|\bar{u}_{\mathrm{eq}-\mathrm{d}}\right|-\epsilon_{\mathrm{d}} $

(18)

$ \dot{\bar{u}}_{\mathrm{eq}-\mathrm{d}}=\frac{1}{\tau_{\mathrm{d}}}\left[-\left(\eta_{\mathrm{d}}+k_{\mathrm{d}}\right) \operatorname{sgn}\left(\sigma_{\mathrm{d}}\right)-\bar{u}_{\mathrm{eq}-\mathrm{d}}\right] $

(19)

$ \frac{1}{4} \epsilon_{\mathrm{d}}^{2}>\delta_{0 \mathrm{d}}^{2}+\frac{1}{\gamma_{\mathrm{d}}}\left(\frac{q_{\mathrm{d}} L_{2}}{\alpha_{\mathrm{d}}}\right)^{2} $

(20)

式中：ρ_d(t)——自适应策略增益项；

δ_d(t)——误差量；

r_d(t)——切换项；

γ_d，δ_0d，r_0d，α_d，ϵ_d，τ_d，q_d——常数；

u_eq-d——自适应滑模扰动观测器中的等效输入；

u_eq-d——等效输入近似值。

其中，常数项满足r_0d，δ_0d，γ_d，ϵ_d，τ_d，q_d > $ \sup \left(1, \left|\frac{\mathrm{d}}{\mathrm{d} t}\left(\dot{u}_{\mathrm{eq}-\mathrm{d}}(t)\right)\right| / L_2\right), 0<\alpha_{\mathrm{d}}<1$。

此时，可确保在有限时间内k_d的值不断更新，最终满足k_d > | L₁ |。

2.3 非奇异有限时间滑模控制器设计

定理2 选取系统滑模面s为

$ \begin{gather*} s=x_{1}^{(n)}+c_{n} \operatorname{sgn}\left(x_{1}^{(n-1)}\right)\left|x_{1}^{(n-1)}\right|^{a_{n}}+\cdots+c_{1} \operatorname{sgn}\left(x_{1}\right)\left|x_{1}\right|^{a_{1}}= \\ \quad \dot{x}_{n}+c_{n} \operatorname{sgn}\left(x_{n}\right)\left|x_{n}\right|^{a_{n}}+\cdots+c_{1} \operatorname{sgn}\left(x_{1}\right)\left|x_{1}\right|^{a_{1}} \end{gather*} $

(21)

式中：n——系统模型阶数，n=1，2，3；

c_n，a_n——滑模面系数。

将控制信号u_i设计为

$ \begin{equation*} u_{i}=\alpha^{-1}\left(u_{\mathrm{eq}}+u_{n}\right) \end{equation*} $

(22)

其中：u_eq=-f(x) - c₃ sgn(x₃)|x₃|^a₃-

$ c_{2} \operatorname{sgn}\left(x_{2}\right)\left|x_{2}\right|^{a_{2}}-c_{1} \operatorname{sgn}\left(x_{1}\right)\left|x_{1}\right|^{a_{1}}-\hat{g}(t) $

(23)

$ \dot{u}_{n}+T u_{n}=u_{\mathrm{s}}, u_{n}(0)=0 $

(24)

$ u_{\mathrm{s}}=-\left(\eta+T\left|u_{n}\right|\right) \operatorname{sgn}(s) $

(25)

式中：u_eq——等效控制信号；

u_n——非线性控制信号；

u_s——控制信号设计过程中的变量值；

T，η——待设计常数。

此时，控制信号u_i可使得系统状态抵达系统滑模面s。在控制信号设计过程中未对滑模面进行微分，从根本上避免了奇异性问题。

证明将控制律u_i代入式（21），可得滑模面s为

$ \begin{equation*} s=u_{n}+g(t)-\hat{g}(t) \end{equation*} $

(26)

设自适应扰动观测器收敛时间为T_C，则t ≥ T_C，s=u_n，则有

$ \begin{equation*} \dot{s}=u_{\mathrm{s}}-T u_{n}=-\left(\eta+T\left|u_{n}\right|\right) \operatorname{sgn}(s)-T u_{n} \end{equation*} $

(27)

选取李雅普诺夫函数V=s² /2，则可推得

$ \begin{gather*} \dot{V}=s \dot{s}=-\eta|s|-T\left|u_{n} \| s\right|-T u_{n} s \leqslant-\eta|s|- \\ T\left|u_{n}\right||s|+T\left|u_{n}\right||s| \leqslant-\eta|s| \end{gather*} $

(28)

由此可得，系统状态可到达滑模面。根据文献[28]，该滑模面可保证系统在有限时间内到达平衡点，使系统频率的有限时间稳定性得到保证。

3 仿真分析

3.1 仿真环境设置

在MATLAB/Simulink中搭建双区域互联电力系统来验证所提出策略的有效性。通过Simulink中的Function模块实现对扰动补偿及终端滑模控制算法的仿真。仿真实验中的系统参数如表 1所示。

表 1 仿真实验的系统参数

下载CSV

区域	M_i/s	D_i/s	T_ti/s	T_gi/s	R_i(p.u.)
1	0.334	0.0083	0.30	0.08	1.25
2	0.400	0.0060	0.25	0.1	1.11

区域	B_i(p.u.)	T_ij（p.u.）	GDB约束值	GRC约束值
1	0.85	0.043	0.2	0.0023
2	0.912	0.043	0.2	0.0023

对于所设计的有限时间滑模控制器，区域1和区域2的滑模面分别为

$ \begin{align*} s_{1}= & \Delta \dddot{f}_{i}+15 \operatorname{sgn}\left(\Delta \ddot{f}_{i}\right)\left|\Delta \ddot{f}_{i}\right|^{7 / 10}+66 \operatorname{sgn}(\Delta \dot{f})|\Delta \dot{f}|^{7 / 13}+ \\ & 80 \operatorname{sgn}\left(\Delta f_{i}\right)\left|\Delta f_{i}\right|^{7 / 16} \end{align*} $

(29)

$ \begin{align*} s_{2}= &\Delta \dddot{f}_{i}+20 \operatorname{sgn}\left(\Delta \ddot{f}_{i}\right)\left|\Delta \ddot{f}_{i}\right|^{7 / 10}+107 \operatorname{sgn}(\Delta \dot{f})|\Delta \dot{f}|^{7 / 13}+\\ & 140 \operatorname{sgn}\left(\Delta f_{i}\right)\left|\Delta f_{i}\right|^{7 / 16} \end{align*} $

(30)

区域1和区域2的控制器待设计常数为：T₁=T₂=0.1；η₁=η₂=0.001。自适应滑模扰动观测器参数为：η_d=0.01；τ_d=0.001；ϵ_d=0.65；α_d=0.999；δ_0d=0.09；γ_d=470；r_0d=0.1；c_1d=2；c_2d=2；α_1d=0.5；α_2d=3。

3.2 负荷扰动下的仿真分析

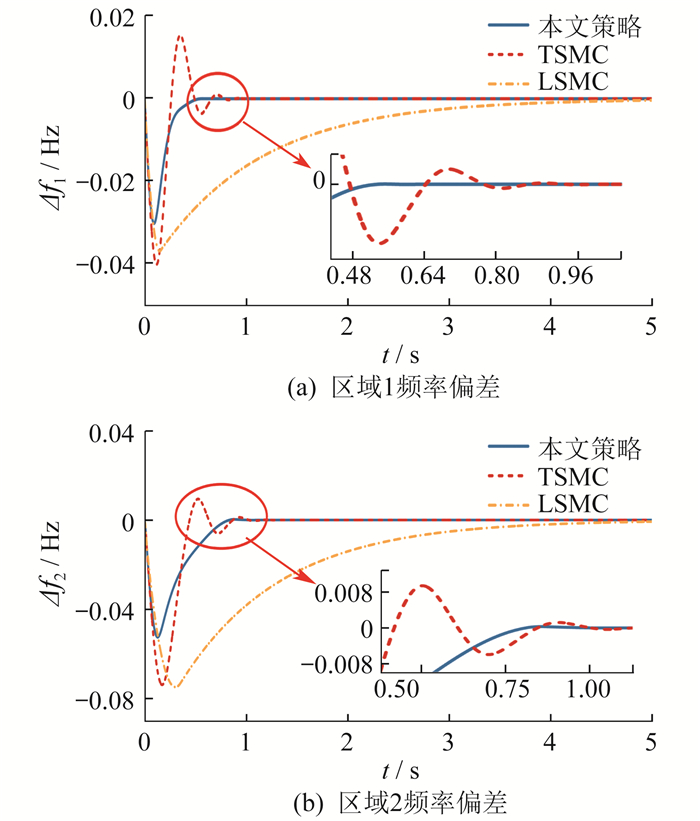
假设区域1和区域2分别受到5% 和10% 的负荷扰动，对所提出的控制策略、无扰动补偿的TSMC和线性滑模控制（Linear Sliding Mode Control，LSMC）进行仿真实验，频率偏差波形如图 2所示。

图 2 负荷扰动下的频率偏差波形

频率响应指标对比如表 2所示。其中，响应时间定义为频率偏差首次恢复到稳定值所需的时间；稳定时间定义为频率保持稳定，且不再发生偏移所需的时间。

表 2 频率响应指标对比

下载CSV

控制策略	区域1最大频率偏差/Hz	区域1响应时间/s	区域1稳定时间/s
本文策略	0.030	0.28	0.49
TSMC	0.039	0.24	0.93
LSMC	0.036	2.29	3.61

控制策略	区域2最大频率偏差/Hz	区域2响应时间/s	区域2稳定时间/s
本文策略	0.052	0.67	0.86
TSMC	0.073	0.42	1.08
LSMC	0.075	2.94	4.31

由图 2和表 2可知，本文所提策略的稳定时间最短，同时频率偏差最小，仅在响应时间上稍逊于TSMC。这是因为TSMC中高扰动估值带来的强控制力，可以快速将频率偏差拉回稳态值，但在返回稳态值附近后，由于缺乏扰动补偿措施，无法完全消除扰动的影响，导致曲线不稳定并继续波动。本文在TSMC的基础上引入了观测器进行扰动补偿，有效解决了这一问题。此外，通过设计自适应律使k_d > |$ {\dot g}$(t)|，观测器可以在有限时间内估计和补偿扰动，无需扰动上界值的相关信息。k_d和|$ {\dot g}$(t)|的变化曲线如图 3所示。

图 3 k_d和|$ {\dot g}$(t)|的变化曲线

3.3 控制性能对比

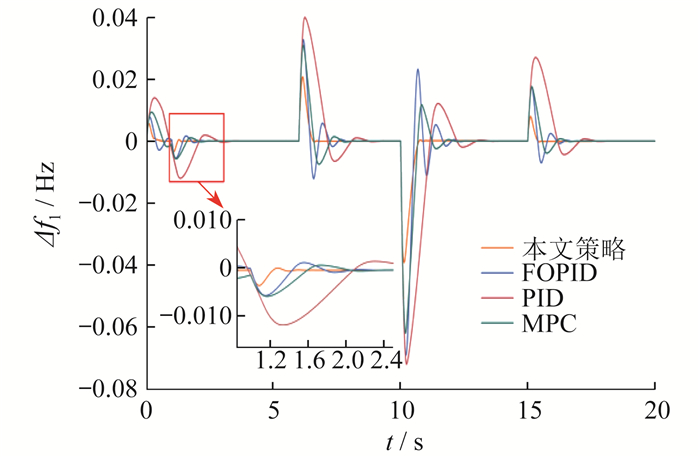
将本文所提控制策略与分数阶PID（Fractional Order PID，FOPID）控制、PID控制和MPC进行性能对比，以更好地评估本文所提策略的优势。选取一种非线性鲁棒模型预测控制进行对比，设计方案及参数的选取参考文献[16]。PID控制器及分数阶PID控制器通过粒子群优化算法选取最优值。区域1中，PID参数为K_P=0.1339，K_Ⅰ=0.527 2，K_D=0.128 5；FOPID参数为K_P1=0.082 3，K_Ⅰ1=0.682 2，K_D1=0.084 9；λ=0.945 7 μ=1.052 4。对于区域1，分别在1、6、10、15 s加入1%、−4%、5% 和−2% 的负荷扰动。不同控制策略的频率偏差如图 4所示。

图 4 不同控制策略的频率偏差

由图 4可以看出，与其他控制策略相比，本文所提策略频率趋于稳定最快、偏差最小，能更好地应对负荷扰动。

4 结语

本文针对含可再生能源的互联电力系统，提出了一种基于自适应扰动补偿的有限时间滑模负荷频率控制策略。仿真结果表明：所提出的控制策略能够有效减少频率稳定所需时间和频率偏差幅值，提高了电力系统的电能质量，使其可以更好地应对新能源输出功率波动以及负荷扰动等问题。另外，本文通过自适应滑模扰动观测器对未知扰动进行了估计与补偿。该补偿项的加入不仅能够减少频率波动，改善系统频率的动态性能，而且对抖振的控制也有一定效果。

参考文献

[1]

杨冬锋, 朱军豪, 姜超, 等. 基于分布式模型预测的高比例风电系统多源协同负荷频率控制策略[J/OL]. 电网技术: 1-14(2023-08-22)[2024-02-20]. https://doi.org/10.13335/j.1000-3673.pst.2023.0889.

[2]

YANG F, SHAO X Y, MUYEEN S M, et al. Disturbance observer based fractional-order integral sliding mode frequency control strategy for interconnected power system[J]. IEEE Transactions on Power Systems, 2021, 36(6): 5922-5932. DOI:10.1109/TPWRS.2021.3081737

[3]

文云峰, 杨伟峰, 林晓煌. 低惯量电力系统频率稳定分析与控制研究综述及展望[J]. 电力自动化设备, 2020, 40(9): 211-222.

[4]

韩云昊, 纪宏澎, 白赫, 等. 柴储混合电力系统的频率协调控制策略[J]. 上海电力学院学报, 2018, 34(6): 577-580. DOI:10.3969/j.issn.1006-4729.2018.06.013

[5]

叶林, 王凯丰, 赖业宁, 等. 低惯量下电力系统频率特性分析及电池储能调频控制策略综述[J]. 电网技术, 2023, 47(2): 446-464.

[6]

王怡, 张浩. 基于模糊控制的风电机组变系数综合惯性控制策略[J]. 上海电力大学学报, 2023, 39(4): 325-331. DOI:10.3969/j.issn.2096-8299.2023.04.003

[7]

符杨, 丁枳尹, 米阳. 计及储能调节的时滞互联电力系统频率控制[J]. 上海交通大学学报, 2022, 56(9): 1128-1138.

[8]

NAHAS N, ABOUHEAF M, SHARAF A, et al. A selfadjusting adaptive AVR-LFC scheme for synchronous generators[J]. IEEE Transactions on Power Systems, 2019, 34(6): 5073-5075. DOI:10.1109/TPWRS.2019.2920782

[9]

SHUKLA H, NIKOLOVSKI S, RAJU M, et al. A particle swarm optimization technique tuned TID controller for frequency and voltage regulation with penetration of electric vehicles and distributed generations[J]. Energies, 2022, 15(21): 8225. DOI:10.3390/en15218225

[10]

王政豪, 刘永慧, 苏庆堂. 基于滑模控制的多区域V2G系统的负荷频率控制[J]. 控制工程, 2022, 29(11): 1981-1988.

[11]

米阳, 郝学智, 刘红业, 等. 基于滑模控制的含风储多域电力系统负荷频率控制[J]. 控制与决策, 2019, 34(2): 437-444.

[12]

PRASAD S, PURWAR S, KISHOR N. Load frequency regulation using observer based non-linear sliding mode control[J]. International Journal of Electrical Power & Energy Systems, 2019, 104: 178-193.

[13]

YANG F, SHEN Y B, LI D D, et al. Fractional-order sliding mode load frequency control and stability analysis for interconnected power systems with time-varying delay[J]. IEEE Transactions on Power Systems, 2024, 39(1): 1006-1018. DOI:10.1109/TPWRS.2023.3242938

[14]

ANSARI J, REZA ABBASI A, BAHMANI FIROUZI B. Decentralized LMI-based event-triggered integral sliding mode LFC of power systems with disturbance observer[J]. International Journal of Electrical Power & Energy Systems, 2022, 138: 107971.

[15]

PRADHAN S K, DAS D K. Sliding mode controller design via delay-dependent H_∞ stabilization criterion for load frequency regulation[J]. Protection and Control of Modern Power Systems, 2023, 8(3): 1-27.

[16]

张海波, 段洁琼, 奚耀冕, 等. 计及储能SOC恢复的孤岛直流外送AGC模型预测控制[J]. 电力自动化设备, 2021, 41(10): 199-204.

[17]

OSHNOEI A, KHERADMANDI M, KHEZRI R, et al. Robust model predictive control of gate-controlled series capacitor for LFC of power systems[J]. IEEE Transactions on Industrial Informatics, 2021, 17(7): 4766-4776.

[18]

GULZAR M M. Designing of robust frequency stabilization using optimized MPC-(1+PIDN)controller for high order interconnected renewable energy based power systems[J]. Protection and Control of Modern Power Systems, 2023, 8(1): 11.

[19]

YU X H, FENG Y, MAN Z H. Terminal sliding mode control -an overview[J]. IEEE Open Journal of the Industrial Electronics Society, 2021, 2: 36-52.

[20]

周铭浩, 苏鸿宇, 周皓宇, 等. 柔性多状态开关全阶终端滑模控制[J]. 中国电机工程学报, 2023, 43(22): 8622-8635.

[21]

QIAN D W, FAN G L. Neural-network-based terminal sliding mode control for frequency stabilization of renewable power systems[J]. IEEE/CAA Journal of Automatica Sinica, 2018, 5(3): 706-717.

[22]

BAGHERI A, JABBARI A, MOBAYEN S. An intelligent ABC-based terminal sliding mode controller for loadfrequency control of islanded micro-grids[J]. Sustainable Cities and Society, 2021, 64: 102544.

[23]

LI S H, SUN H B, YANG J, et al. Continuous finite-time output regulation for disturbed systems under mismatching condition[J]. IEEE Transactions on Automatic Control, 2015, 60(1): 277-282.

[24]

RASHAD R, EL-BADAWY A, ABOUDONIA A. Sliding mode disturbance observer-based control of a twin rotor MIMO system[J]. ISA Transactions, 2017, 69: 166-174.

[25]

SUN T R, CHENG L, WANG W Q, et al. Semiglobal exponential control of Euler-Lagrange systems using a sliding-mode disturbance observer[J]. Automatica, 2020, 112: 108677.

[26]

GUO J P. Application of full order sliding mode control based on different areas power system with load frequency control[J]. ISA Transactions, 2019, 92: 23-34.

[27]

EDWARDS C, SHTESSEL Y B. Adaptive continuous higher order sliding mode control[J]. Automatica, 2016, 65: 183-190.

[28]

BHAT S P, BERNSTEIN D S. Geometric homogeneity with applications to finite-time stability[J]. Mathematics of Control, Signals, and Systems, 2005, 17(2): 101-127.