|
|
|
发布时间: 2024-10-28 |
特约专栏:电力系统先进控制技术 |
|
|
|
收稿日期: 2024-04-11
基金项目: 上海市自然基金(20ZR1421300)
中图法分类号: TP273
文献标识码: A
文章编号: 2096-8299(2024)05-0415-06
|
摘要
针对低温多效蒸馏(LT-MED)海水淡化系统中冷凝器出口海水温度控制问题,在蝴蝶优化算法(BOA)的基础上,提出了一种改进BOA-PID控制方法,并利用MATLAB软件搭建仿真模型,将改进BOAPID控制的控制效果与BOA-PID控制、常规PID控制进行对比。结果表明,改进BOA-PID在适应度值和全局搜索能力方面表现卓越;与常规PID控制相比,基于改进BOA-PID控制系统中相应的优化程序能够自动整定各个参数,提升了系统的响应速度,大幅减小了超调量,提升了海水淡化系统的造水比,系统能正常运行。
关键词
低温多效蒸馏; 冷凝器; 海水温度控制; 比例积分微分控制; 蝴蝶优化算法
Abstract
A modified BOA-PID control method is proposed based on the butterfly optimization algorithm(BOA)to address the temperature control problem at the outlet of the condenser in the low temperature-multi effect distillation(LT-MED)seawater desalination system. A simulation model is constructed using MATLAB software to compare the control effect of the improved BOA-PID control with BOA-PID control and conventional PID control. The results show that the improved BOA-PID performs excellently in terms of fitness values and global search ability; compared with conventional PID control, the corresponding optimization program in the improved BOA-PID control system can automatically adjust various parameters, improve the response speed of the system, significantly reduce overshoot, improve the water production ratio of the seawater desalination system, and enable the system to operate normally.
Key words
low temperature-multi effect distillation; condenser; seawater temperature control; proportional integral differential control; butterfly optimization algorithm
由于社会经济的高速发展,淡水资源日渐贫乏。综合研究海水淡化过程中的水处理技术发现,低温多效蒸馏(Low Temperature-Multi Effect Distillation,LT-MED)海水淡化技术具有能耗低的优良品质[1]。LT-MED海水淡化技术在淡水生产过程中会受到压力、温度、流量、液位等因素的影响,因此需要对上述因素进行有效把握。当海水淡化系统正常运行时,进入冷凝器的进料海水温度较低,当海水喷洒到首效蒸发器上,部分热源会用于提高海水温度,从而导致首效蒸发器淡水产量减少。文献[2]利用Aspen Plus流程模拟软件研究了LT-MED系统的进料方式。研究结果表明,当冷凝器出口海水温度保持在40.7 ℃时,系统造水比提升较大[3]。因此,对冷凝器出口海水温度进行控制十分必要。
比例积分微分(Proportional Integral Derivative,PID)控制常被用于冷凝器出口海水温度控制,但其对于复杂控制系统(如串级、分程、解耦等)的控制效果不能令人满意[4]。近年来,研究人员将优化算法与PID控制相结合,以达到优化PID控制参数的效果。文献[5]利用动态惯性权重对粒子群算法进行改进,减小了控制系统的超调量,缩短了过渡时间;文献[6]通过蝙蝠优化算法提高了参数精度;文献[7]通过改进天牛算法的采煤机牵引PID控制系统,明显改善了控制效果。另外,有研究人员从进料方式、结垢影响等方面入手,通过控制系统温度提高海水淡化系统的造水比。文献[8]结合变论域思想,通过训练伸缩因子得到了末效浓盐水温度控制的传递函数;文献[9]设计了首效出口凝结水自抗扰温度控制器;文献[10]利用菌群及粒子群算法的优势,提高了首效出口凝结水温度控制系统的鲁棒性;文献[11]针对末效浓盐水温度控制系统,设计了一种基于改进鲸鱼算法的PID控制器,具有更快的响应速度。
本文在蝴蝶优化算法[12](Butterfly Optimization Algorithm,BOA)的基础上,设计一种改进BOA-PID控制器,用以控制LT-MED海水淡化系统中冷凝器出口海水的温度,并通过仿真实验验证优化后PID控制器的有效性。
1 冷凝器出口海水温度控制系统模型
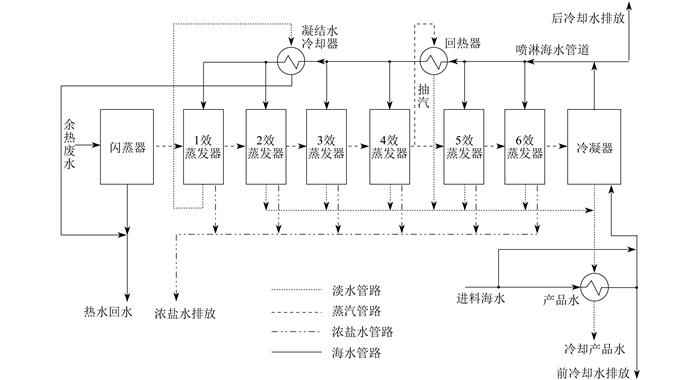
1.1 LT-MED海水淡化系统流程
1.2 冷凝器出口海水温度特性分析
通过测温传感器将出口海水的温度特性数据反馈至计算机。将进入冷凝器前的海水温度作为系统的输入值,由于水的比热容较大,对热量的吸收存在时滞性,故可用延迟环节对其近似;系统的输出值为离开冷凝器后的海水温度,此过程可用一个一阶惯性环节对其近似。
冷凝器出口海水温度控制系统传递函数公式为
| $ \begin{equation*} G(s)=\frac{K \mathrm{e}^{-\tau s}}{T_{0} s+1} \end{equation*} $ | (1) |
式中:G(s)——传递函数;
s——拉普拉斯算子;
K——比例放大系数;
e-τs——延迟环节;
τ——纯滞后时间;
T0——时间常数。
当τ/T0>0.5时,该控制系统称为大时滞系统[14]。经系统辨识算法可得传递函数中各参数值分别为:K = 5,T0 = 4,τ = 6。
将延迟环节中的eτs用泰勒级数展开为
| $ \mathrm{e}^{\tau s}=1+\frac{\tau s}{1!}+\frac{\tau^{2} s^{2}}{2!}+\frac{\tau^{3} s^{3}}{3!}+\ldots, -\infty<\tau s<\infty $ | (2) |
取eτs = 1 + τs,则传递函数为
| $ \begin{equation*} G(s)=\frac{5}{(4 s+1)(6 s+1)} \end{equation*} $ | (3) |
2 基于改进BOA的PID控制器设计
2.1 BOA描述
假设种群中存在香气最浓郁的蝴蝶个体,当其他蝴蝶闻到其香气时,就会不断向它聚集,此过程叫做全局搜索阶段;当其他蝴蝶没有闻到香气时,会在一定空间里随机移动,此过程叫做局部搜索阶段。在整个搜索过程中,全局搜索阶段和局部搜索阶段相互转换的依据是转换概率p的大小[15]。香味刺激系数的计算公式为
| $ F=c I^{\alpha} $ | (4) |
式中:F——香味刺激系数,与蝴蝶位置有关;
c——感知因子;
I——刺激强度;
α——激励指数,α ∈[0, 1]。
每次迭代开始时,在[0, 1]区间中任取一数r。若r<p(p一般取0.8),则进入全局搜索阶段;否则,进入局部搜索阶段。两个阶段的计算公式分别为
| $ \begin{gather*} \boldsymbol{x}_{i}^{t+1}=\boldsymbol{x}_{i}^{t}+\left(r^{2} \boldsymbol{g}-\boldsymbol{x}_{i}^{t}\right) F \end{gather*} $ | (5) |
| $ \boldsymbol{x}_{i}^{t+1}=\boldsymbol{x}_{i}^{t}+\left(r^{2} \boldsymbol{x}_{j}^{t}-\boldsymbol{x}_{k}^{t}\right) F $ | (6) |
式中:xit,xjt,xkt——第t次迭代中第i个、第j个和第k个个体的具体位置;
g——种群中香味最浓郁的个体所在位置。
2.2 改进BOA的原理
与其他智能优化算法类似,BOA存在容易陷入局部最优、收敛速度慢等问题。针对这些问题,本文从3个方面对BOA进行改进,即改进算法参数(转换概率)、改进自适应惯性权重因子、改进局部搜索策略。
2.2.1 改进算法参数
在BOA中,转换概率p为固定值,就导致了算法的全局搜索能力较弱,局部搜索收敛速度慢[16]。针对这一问题,本文采用转换概率自适应调整机制[17]。该机制能够动态切换全局搜索与局部搜索,使算法前期快速定位至全局最优解,后期加快收敛速度。改进转换概率的更新公式为
| $ \begin{equation*} p_{i}=\frac{\lg \left|f_{\min }(t)\right|+f_{\min }(t)}{\lg \left|f_{i}(t)\right|+f_{i}(t)} \cdot\left(p_{\max }-p_{\min }\right) \end{equation*} $ | (7) |
式中:pi——第i个个体的转换概率;
fmin(t)——第t次迭代时种群的最优适应度;
fi(t)——第t次迭代时第i个个体的适应度;
pmax,pmin——转换概率的最大值、最小值。
2.2.2 改进自适应惯性权重因子
为了更好地适应改进后算法的全局搜索能力和局部搜索能力,在算法的前期,增大惯性权重因子,以跳出该区域的局部最优解;在算法的后期,减小惯性权重因子,以提高该区域的收敛速度。自适应惯性权重因子w[18]的计算公式,以及改进后的BOA全局搜索位置更新公式为
| $ w=0.8 \times \exp \left(-\frac{20 t}{T}\right)^{7} $ | (8) |
| $ \boldsymbol{x}_{i}^{t+1}=\boldsymbol{x}_{i}^{t} w+\left(r^{2} \boldsymbol{g}-\boldsymbol{x}_{i}^{t}\right)F $ | (9) |
式中:T——最大迭代次数。
2.2.3 改进局部搜索策略
在局部搜索阶段,蝴蝶个体会在一定空间内随机移动,不易查找最优适应度,且容易陷入局部最优。为了使BOA能快速跳出局部最优,本文引入高斯函数对局部搜索阶段进行干扰[19]。干扰公式为
| $ \begin{equation*} \delta(t)=\exp \left(-\frac{20 t}{T}\right)^{6} \end{equation*} $ | (10) |
式中:δ (t)——高斯干扰函数。
引入高斯干扰函数后的局部搜索位置更新公式为
| $ \boldsymbol{x}_i^{t+1}=\operatorname{Gaussian}[0, \delta(t)]\left[\boldsymbol{x}_i^t+\left(r^2 \boldsymbol{x}_j^t-\boldsymbol{x}_k^t\right) F\right] $ | (11) |
式中:Gaussian[0,δ(t)]——高斯函数,其位置和宽度随着迭代次数的变化而变化。
2.3 基于改进BOA的PID控制
2.3.1 改进的BOA-PID控制系统
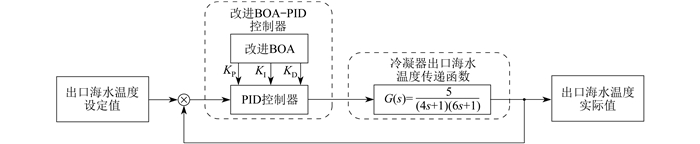
本文以LT-MED海水淡化系统中冷凝器出口海水温度作为研究对象,改进BOA优化PID控制系统原理如图 2所示。其中,KP、KI、KD为PID控制器参数。
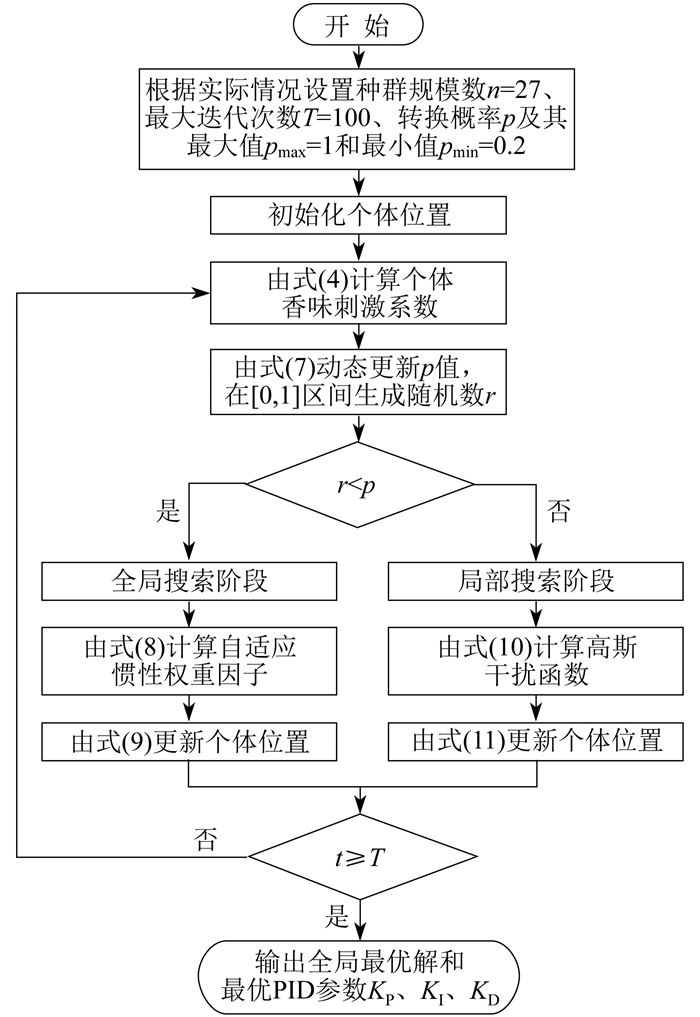
2.3.2 改进BOA优化PID控制器参数流程
基于改进BOA优化PID控制器参数流程如图 3所示。
3 仿真实验与结果分析
3.1 两种控制器的参数
在MATLAB软件中搭建冷凝器出口海水温度控制系统模型,通过多次调整PID控制器参数,即可获得在模拟环境温度为40.7 ℃时对系统的模拟响应。此时,相应的PID控制器参数为:KP = 2.105 7,KI = 0.289 9,KD = 3.222 4。
在改进算法中依次设置相关参数,经过多次调试得到:BOA-PID控制器参数上界Ub为[25, 12, 12],参数下界Lb为[0, 0, 0];改进BOA-PID控制器参数为KP = 5.488 3,KI = 0.690 1,KD = 8.164 7。
3.2 仿真模型与结果
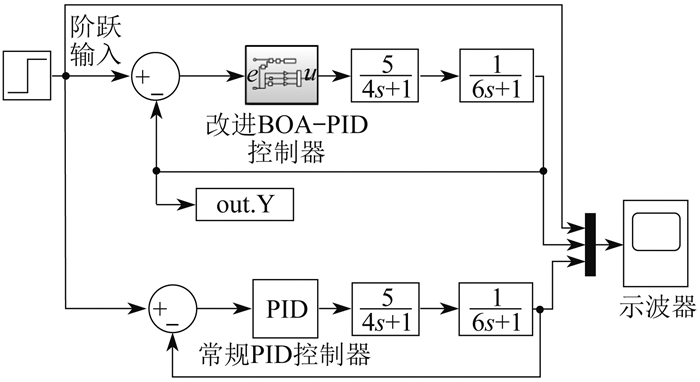
本文搭建的控制系统模型由常规PID控制器和改进BOA-PID控制器两部分组成。其在MATLAB中的Simulink仿真模型如图 4所示。其中:e、u分别为改进BOA-PID控制器的输入值和优化后PID控制器的输出值;out.Y模块可将输出数据导入至工作区。
将常规PID控制、BOA-PID控制、改进BOA-PID控制3种控制方法的响应曲线与阶跃响应曲线进行对比,结果如图 5所示。
由 图 5可知,与常规PID控制相比,改进BOA-PID控制在超调量、响应速度、上升时间、稳定性等方面均更优。与BOA-PID控制相比,改进BOA-PID控制的超调量大幅减小,稳定效果明显改善。
3种控制方式在模拟环境温度下的性能指标和控制器参数值如表 1所示。
表 1
3种控制方式在模拟环境温度下的性能指标和控制器参数值
| 控制器 | 超调量/% | 上升时间/s | 峰值时间/s | 调节时间/s | KP | KI | KD |
| 常规PID | 12.70 | 3.912 | 4.398 | 16.083 | 2.105 7 | 0.289 9 | 3.222 4 |
| BOA-PID | 10.15 | 2.605 | 3.886 | 12.242 | 3.845 5 | 0.650 3 | 5.395 5 |
| 改进BOA-PID | 6.02 | 2.463 | 3.554 | 10.660 | 5.488 3 | 0.690 1 | 8.164 7 |
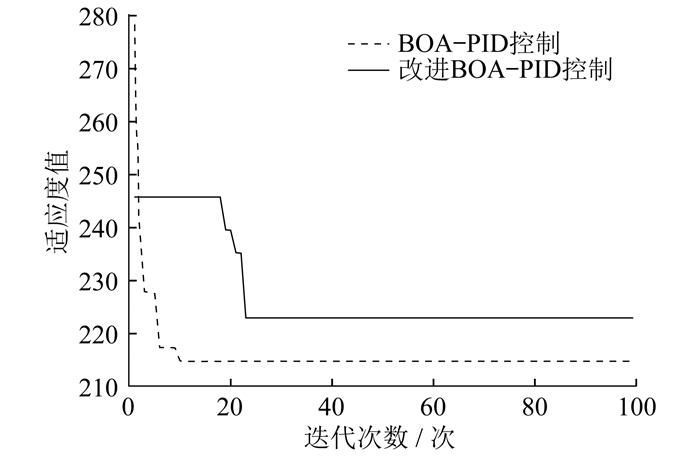
BOA-PID控制与改进BOA-PID控制的迭代效果对比如图 6所示。
由图 6可知,改进BOA-PID控制器迭代到第11次时,已找到最优适应度值,BOA-PID控制器则需要迭代到23次,才找到最优适应度值,且改进BOA-PID控制器的适应度值更小,有利于系统的正常运行。
4 结论
本文从转换概率、自适应惯性权重因子、局部搜索策略3个方面对BOA-PID控制进行改进。改进后的BOA-PID控制器能较好地实现对冷凝器出口海水温度的控制,在保障系统正常运行的同时,优化淡水产量,并发挥最大的经济效益。根据实验结果可得出以下结论。
(1)与常规PID控制相比,改进BOA-PID控制具有良好的动态响应和静态响应性能,使系统的控制效果得到明显改善,且出口海水温度控制系统能够正常运行。
(2)与BOA-PID控制相比,改进BOA-PID控制的局部与全局搜索能力得到增强,可以避免系统陷入局部最优状态,且超调量减小,稳定性增强。
参考文献
-
[1]尹建华, 吕庆春, 阮国岭. 低温多效蒸馏海水淡化技术[J]. 海洋技术, 2002, 21(4): 22-26.
-
[2]卢涛, 陈军, 沈胜强. 低温多效蒸发海水淡化系统不同进料方式的热力学分析[J]. 热科学与技术, 2012, 11(2): 142-147.
-
[3]卢涛, 陈军, 沈胜强. 低温多效蒸发海水淡化系统顺流进料工艺流程模拟及经济评估[J]. 热科学与技术, 2013, 12(3): 189-194.
-
[4]吴永志, 吴刚. 低温多效海水淡化装置在不同工况下的应用[J]. 冶金动力, 2019(2): 63-66.
-
[5]马帅, 王玉有, 杨理, 等. 基于改进粒子群优化PID的矿用机电设备控制策略[J]. 工业仪表与自动化装置, 2023(5): 115-119.
-
[6]宫佳. 基于蝙蝠算法的PID控制参数优化技术与仿真研究[J]. 河南工程学院学报(自然科学版), 2023, 35(3): 67-70.
-
[7]南鹏飞. 基于改进天牛须算法和永磁同步电机的采煤机牵引电机控制[J]. 煤矿机械, 2023, 44(9): 33-36.
-
[8]鲍克勤, 孙蕊, 黄伟. 基于变论域模糊理论的海水淡化温控系统[J]. 计算机仿真, 2020, 37(8): 148-152.
-
[9]鲍克勤, 刘擘, 汤豪. 基于LADRC的低温多效海水淡化温度控制[J]. 昆明理工大学学报(自然科学版), 2022, 47(1): 38-45.
-
[10]鲍克勤, 阮绵虎, 汤豪. 基于BFO-PSO的LT-MED海水淡化温度控制[J]. 上海电力大学学报, 2023, 39(2): 189-194.
-
[11]王旻洁, 杨蒙姣, 毛涧. 基于改进WOA-PID的LT-MED系统浓盐水温度控制[J]. 上海电力大学学报, 2023, 39(4): 387-392.
-
[12]孙林, 陈岁岁, 徐久成, 等. 基于交叉迁移和共享调整的改进蝴蝶优化算法[J]. 计算机应用研究, 2020, 37(3): 799-804.
-
[13]张毅. 换流阀余热回收利用热力系统性能与热经济性研究[D]. 北京: 北京建筑大学, 2020.
-
[14]王琦, 韩天兴, 贾伟, 等. 基于模糊自适应PID的储能电池集装箱温度控制[J]. 自动化技术与应用, 2020, 39(5): 1-5.
-
[15]丁元明, 夏清雨, 张然, 等. 蝴蝶优化算法研究综述[J]. 科学技术与工程, 2023, 23(7): 2705-2716.
-
[16]齐高峰, 杜齐, 郭文豪, 等. 改进BOA-PO算法下局部遮荫光伏最大功率跟踪控制[J/OL]. 计算机仿真, 2023: 1-7[2024-02-29]. http://kns.cnki.net/kcms/detail/11.3724.TP.20230924.1138.003.html.
-
[17]张晶, 曲悦, 张家洪, 等. 混合灰狼-自适应蝴蝶算法下的多目标无线传感器网络覆盖研究[J/OL]. 小型微型计算机系统, 2023: 1-10[2024-02-29]. http://kns.cnki.net/kcms/detail/21.1106.TP.20230518.1428.014.html.
-
[18]韦修喜, 彭茂松, 黄华娟. 基于多策略改进蝴蝶优化算法的无线传感网络节点覆盖优化[J]. 计算机应用, 2024, 44(4): 1009-1017.
-
[19]王仲英, 刘秋菊. 改进蝴蝶算法优化支持向量机的土壤含水量预测模型[J]. 计算机工程与设计, 2023, 44(2): 612-621.