|
|
|
发布时间: 2024-10-28 |
智能电网技术 |
|
|
|
收稿日期: 2024-04-03
中图法分类号: TM734
文献标识码: A
文章编号: 2096-8299(2024)05-0421-08
|
摘要
为提高同一区域多个不同利益主体的微电网低碳经济运行,提出了一种考虑风光不确定性的多微电网主从博弈低碳优化方法。首先,基于多智能体技术,建立以多微电网运营商为领导者、各微电网为跟随者的多微电网系统能量交互模型。其次,针对风光不确定性,并考虑各主体的运行成本、碳交易成本,建立基于条件风险价值的主从博弈模型。最后,结合遗传算法和CPLEX求解器进行求解。结果表明,该优化策略可以有效提高各主体的经济性,促进可再生能源消纳,降低碳排放量。
关键词
多微电网系统; 主从博弈; 多智能体; 碳交易; 不确定性
Abstract
To improve the low-carbon economic operation of multi-microgrid with different stakeholders in the same region, a multi-microgrid Stackelberg game low-carbon optimization method considering wind and solar uncertainty is proposed. Firstly, based on multi-agent technology, an energy interaction model for a multi-microgrid system with multi-microgrid operators as leaders and each microgrid as followers is established. Then, Stackelberg game model based on conditional risk value is established to address the uncertainty of wind and solar energy, considering the operating costs and carbon trading costs of each entity. Finally, the genetic algorithm and CPLEX solver are combined to solve the problem. The results show that this optimization strategy can effectively improve the economic efficiency of each entity, promote the consumption of renewable energy, and reduce carbon emissions.
Key words
multi-microgrid system; Stackelberg game; multi-agent system; carbon trading; uncertainty
在全球能源短缺和环境污染的背景下,为了实现“双碳”目标,提高清洁能源利用率、减少碳排放等是我国电力系统的重要方向[1-2]。在此形势下,微电网技术应运而生。多个相邻微电网组成多微电网可以实现系统内多能源能量耦合,提高能源利用率,同时有效降低系统的碳排放量。然而,多微电网系统的快速发展以及可再生能源复杂的波动性和间歇性,给多微电网系统的调度带来了困难[3]。因此,如何实现区域多微电网的安全经济运行以及平衡多个不同主体间的利益冲突亟待研究。
从已有的研究来看,博弈论是协同多微电网多个主体之间利益和保护信息隐私的重要方法之一,主要分为非合作博弈和合作博弈。文献[4]提出了能量管理中心和微电网运营商的非合作博弈模型,使双方利益最大化,减小了内部电价的剧烈波动。文献[5]提出了多微电网和含热电耦合负荷间的非合作主从博弈协同优化。然而,非合作博弈中的每一个主体都是自私的,缺乏对整体利益的考虑。合作博弈首先考虑的是整体利益最大化,其次是利益分配。文献[6]基于多个光伏微电网协同的合作博弈,通过Shapley值法将通过合作提高的收益分配给每个微电网。文献[7]改进了Shapley值法,基于功率交互贡献度减少了多个微电网时的计算量。然而,对于更多数量的微电网,计算量与耗时仍难以解决。文献[8]建立了点对点能量交易模型,通过交替方向乘子法进行分布式求解。
以上的研究深入分析了多微电网的利益分配。然而,多微电网系统在运行中存在风电、光伏等不确定因素。文献[9]采用数据驱动算法描述风电、光伏不确定性,提高了调度的经济性。文献[10]采用两阶段鲁棒博弈,通过区块链技术提高了整体经济性。文献[11]利用随机场景生成建立双主体博弈优化,实现了双赢。文献[12]采用了双层多场景协同优化,基于Frank-Copula函数生成风光不确定性场景,有效验证了多微电网间的协同优化,但未考虑碳交易机制与不确定性下多微电网协同运行对经济性和低碳的影响。
本文提出了多智能体技术下考虑风光不确定性的多微电网低碳优化模型。该模型是以多微电网运营商为领导者、以微电网智能体(Microgrid Agent,MGA)为跟随者的主从博弈模型。针对风光不确定性,采用条件风险价值度量多微电网间的功率传输风险,并通过碳交易机制约束碳排放量,以各主体的经济性最优为目标函数建立模型。通过遗传算法和CPLEX求解器进行求解,通过仿真证明该模型有效提高了各主体的经济性,有效消纳了可再生能源并减少了碳排放量。
1 基于多智能体的多微电网系统模型
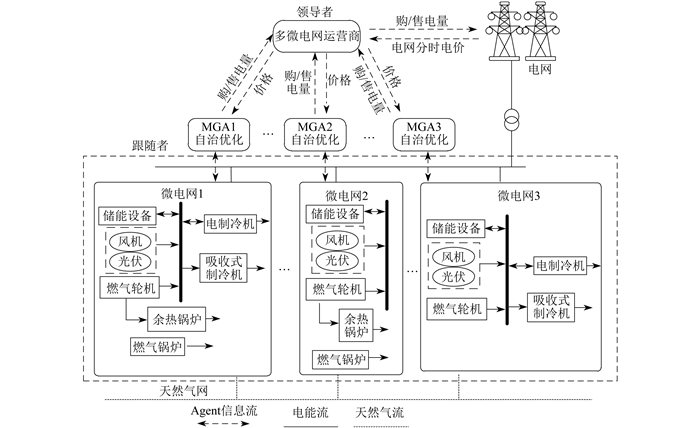
本文研究的多微电网系统框架如图 1所示。多微电网运营商从上级电网购电。上层领导者为多微电网运营商,由多个微电网组成。下层结构是MGA,由微电网的分布式电源构成,通过天然气网购气,利用燃气设备供电供热。冷热电热联供(Combined Cooling Heating and Power,CCHP)型微电网是MGA的典型结构,MGA模型包括风电机组、光伏机组、微型燃气轮机、余热锅炉、燃气锅炉、吸收式制冷机、电制冷机、储能设备,负载主要包括电、热、冷负荷。
本文建立了基于多智能体系统的多微电网能量交互模型,不同利益主体的多微电网运营商与MGA为一主多从的动态博弈。多微电网运营商在电网购售电价范围内使多微电网运营商和各微电网的利益最大化。多微电网运营商根据系统整体的功率缺盈情况,鼓励微电网内部能量交互,并与上级电网购售电,在多方主体的协同下实现能量经济优化。
2 主从博弈模型
2.1 上层多微电网运营商模型
多微电网运营商根据与上级电网、气网购能以及各个微电网购售电量,制定多微电网系统内部电价,实现多微电网系统运行成本最小。
2.1.1 目标函数
多微电网系统的目标函数为
| $ \min f_{\mathrm{MMGA}}=C_{i, \text { trade }}(t)+C_{\mathrm{grid}}(t)+C_{\mathrm{gas}}(t) $ | (1) |
| $ C_{i, \text { trade }}(t)=\sum\limits_{t=1}^T \sum\limits_{j=1, j \neq i}^n\left[\rho_{i j}(t) P_{i j}(t)\right] $ | (2) |
| $ C_{\text {grid }}(t)=\sum\limits_{t=1}^T \delta_{\text {buy }}(t) P_{\text {buy }}(t)-\delta_{\text {sell }}(t) P_{\text {sell }}(t) $ | (3) |
| $ C_{\text {gas }}(t)=\sum\limits_{t=1}^T c_{\text {buy }}^{\text {gas }}(t) P_{\text {buy }}^{\text {gas }}(t) $ | (4) |
式中:Ci,trade(t)——多微电网运营商与微电网i之间的交互成本;
Cgrid(t)——多微电网运营商与上级电网的交互成本;
Cgas(t)——多微电网运营商与上级气网的购气成本;
T——一日划分时段总数,取24;
n——微电网数量;
ρij(t)——t时段微电网与多微电网运营商的内部实时电价;
Pij(t)——t时段微电网i与多微电网运营商购售的交互电量;
δbuy(t),δsell(t)——t时段电网间的购售电价;
Pbuy(t),Psell(t)——t时段多微电网运营商与电网的购售电量;
cbuygas(t)——多微电网运营商向上级气网购气单价;
Pbuygas(t)——多微电网运营商向上级气网购气功率。
2.1.2 约束条件
(1) 多微电网购售电量平衡:
| $ -P_{\mathrm{e}, i}^{\min } \leqslant P_{i j}(t) \leqslant P_{\mathrm{e}, i}^{\max } $ | (5) |
式中:Pe,imax,Pe,imin——微电网与多微电网交易的电功率上下限。
(2) 为了保护电力公司的利益并激励微电网间的电能交互,购售电价需满足在电网电价规定的区间内,即
| $ \delta_{\text {sell }}(t)<\rho_{i j}(t)<\delta_{\text {buy }}(t) $ | (6) |
2.2 下层MGA模型
2.2.1 优化目标
在下层MGA跟随者模型中,各微电网的优化目标为运行成本最小。同时,各微电网根据上层多微电网运营商所制定的内部电价,参与主从博弈,积极灵活地调整自身的运行计划,降低用能成本。
其目标函数为
| $ \begin{aligned} \min f_{\mathrm{MGA}}= & C_{i, \mathrm{wh}}(t)+C_{i, \mathrm{gq}}(t)+C_{i, \mathrm{p}}(t)+C_{i, \mathrm{CO}_2}(t)+ \\ & C_{i, \text { trade }}(t) \end{aligned} $ | (7) |
式中:Ci,wh(t)——设备的运行维护成本;
Ci,gq(t)——购买天然气成本;
Ci,p(t)——弃风弃光惩罚成本;
Ci,CO2 (t)——碳交易成本。
(1) 设备的运行维护成本:
| $ \begin{aligned} & C_{i, \mathrm{wh}}(t)=k_{\mathrm{GT}} P_{i, \mathrm{GT}}(t)+k_{\mathrm{GB}} Q_{i, \mathrm{~GB}}(t)+ \\ & k_{\mathrm{WHB}} Q_{i, \mathrm{WHB}}(t)+k_{\mathrm{EC}} Q_{i, \mathrm{EC}}(t)+ \\ & k_{\mathrm{CR}} P_{i, \mathrm{CR}}(t)+k_{\mathrm{PVI}} P_{i, \mathrm{PVI}}(t)+ \\ & k_{\mathrm{WTI}} P_{i, \mathrm{WTI}}(t)+k_{\mathrm{B}}\left|P_{i, \mathrm{~B}}(t)\right| \end{aligned} $ | (8) |
式中:kGT,kGB,kWHB,kEC——燃气轮机、燃气锅炉、余热锅炉、吸收式电制冷机的单位功率运行维护成本;
Pi,GT(t),Qi,GB(t),Qi,WHB(t)——t时段微电网i的微型燃气轮机发电功率、燃气锅炉的输出热功率、余热锅炉输出的热功率;
Qi,EC(t),Pi,CR(t)——t时段微电网i的电制冷机输出的制冷功率、吸收式电制冷机输出的冷功率;
kCR,kPVI,kWTI,kB——电制冷机、风机、光伏、储能的单位功率运行维护成本;
Pi,PVI(t),Pi,WTI(t)——t时段微电网i的光伏、风机发电功率;
Pi,B(t)——t时段储能功率。
(2) 购买天然气成本:
| $ C_{i, \mathrm{gq}}(t)=c_{\mathrm{gq}}\left[\frac{P_{i, \mathrm{GT}}(t)}{L_{\mathrm{gq}} \eta_{\mathrm{GT}}}+\frac{Q_{i, \mathrm{~GB}}(t)}{L_{\mathrm{gq}} \eta_{\mathrm{GB}}}\right] $ | (9) |
式中:cgq——天然气单价;
Lgq——燃气热值;
ηGT,ηGB——微型燃气轮机、燃气锅炉效率。
(3) 弃风弃光惩罚成本:
| $ \begin{aligned} & C_{i, \mathrm{p}}(t)= \\ & \quad \delta_{\mathrm{p}}\left\{\left[P_{i, \mathrm{WTI}}(t)-P_{i, \mathrm{WT}}(t)\right]+\left[P_{i, \mathrm{pVI}}(t)-P_{i, \mathrm{pV}}(t)\right]\right\} \end{aligned} $ | (10) |
式中:δp——弃风弃光惩罚系数;
Pi,WT(t),Pi,PV(t)——t时段微电网i消耗的风电、光伏功率。
(4) 碳交易成本。电力行业对微电网每个主体发放初始免费的碳排放额度。微电网碳排放量小于碳排放额度时,市场给予奖励;反之,微电网需要缴纳罚金。本文系统的无偿碳排放配额主要包括外部电网购电、CCHP机组的无偿碳排放配额,电网购电默认为燃煤机组发电。碳交易的无偿碳排放配额为
| $ E_{i, \mathrm{c}}=E_{i, \mathrm{Grid}}+E_{i, \mathrm{CCHP}} $ | (11) |
| $ E_{i, \text { Grid }}=\sum\limits_{t=1}^{24} \delta_{\mathrm{e}} P_{i, \text { buy }}(t) $ | (12) |
| $ E_{i, \mathrm{CCHP}}=\sum\limits_{t=1}^{24} \delta_{\mathrm{h}}\left[\varphi P_{i, \mathrm{GT}}(t)+\delta_{\mathrm{h}} Q_{i, \mathrm{~GB}}(t)\right] $ | (13) |
式中:Ei,c——微电网i的碳排放配额;
Ei,Grid,Ei,CCHP——微电网i的外部电网购电、CCHP无偿碳排放配额;
δe,δh——单位电量、热量碳排放分配额;
Pi,buy(t)——t时段微电网i从外部电网购买的电量;
φ——发电量折算成供热量的折算系数。
实际碳排放量为
| $ \begin{aligned} E_{i, \mathrm{r}}= & \sum\limits_{t=1}^{24} a_1+b_1 P_{i, \text { buy }}(t)+c_1\left[P_{i, \text { buy }}(t)\right]^2+a_2+ \\ & b_2 P_{i, \mathrm{CCHP}}(t)+c_2\left[P_{i, \mathrm{CCHP}}(t)\right]^2 \end{aligned} $ | (14) |
| $ P_{i, \mathrm{CCHP}}(t)=P_{i, \mathrm{GT}}(t)+Q_{i, \mathrm{~GB}}(t) $ | (15) |
因此,微电网的碳交易成本为
| $ C_{i, \mathrm{CO}_2}=\rho_{\mathrm{CO}_2}\left(E_{i, \mathrm{c}}-E_{i, \mathrm{r}}\right) $ | (16) |
式中:a1,b1,c1,a2,b2,c2——对应机组碳排放量系数;
Pi,CCHP(t)——微电网i的CCHP有功功率;
ρCO2——碳交易基价,取0.252元/kg。
2.2.2 约束条件
多微电网系统的约束条件包括各设备的平衡约束条件、微电网内部的冷热电能量平衡约束条件、风电和光伏发电的功率输出约束条件和电力交易约束条件。
(1) 电、热、冷功率平衡约束条件:
| $ \begin{aligned} & P_{i, \mathrm{GT}}(t)+P_{i, \mathrm{WT}}(t)+P_{i, \mathrm{PV}}(t)+P_{i, \text { buy }}(t)+P_{i, \text { dis }}^{\mathrm{ES}}(t)= \\ & L_{i, \mathrm{EL} \text {oad }}(t)+P_{i, \text { sell }}(t)+P_{i, \mathrm{ch}}^{\mathrm{ES}}(t)+P_{i, \mathrm{EC}}(t)+P_{\mathrm{e}, i j}(t) \end{aligned} $ | (17) |
| $ Q_{i, \mathrm{~GB}}(t)+Q_{i, \mathrm{GT}}(t)=L_{i, \text { HLoad }}(t) $ | (18) |
| $ Q_{i, \mathrm{EC}}(t)+Q_{i, \mathrm{CR}}(t)=L_{i, \mathrm{CLoad}}(t) $ | (19) |
式中:Pi,disES(t),Pi,chES(t)——t时段储能的放电和充电功率;
Li,ELoad(t),Li,HLoad(t),Li,CLoad(t)——t时段微电网i的电、热、冷负荷;
Pi,sell(t)——微电网i的购电功率;
Pi,EC(t)——t时段微电网i的吸收式电制冷机的输出功率;
Qi,GT(t)——t时段微电网i的燃气轮机输出的热功率。
(2) 微电网间传输功率约束条件:
| $ -P_{\mathrm{MG}}^{\min } \leqslant P_{\mathrm{MG}, i j}(t) \leqslant P_{\mathrm{MG}}^{\max } $ | (20) |
式中:PMGmax,PMGmin——微电网间传输功率上下限;
PMG,ij(t)——微电网间传输功率。
2.3 条件风险价值模型
考虑到风光不确定性的影响,利用蒙特卡洛法随机抽样和K-means聚类得到典型场景,并采用笛卡尔乘积联合与同步回代消除法削减场景,得到典型风光联合输出功率场景。CVaR能够深入考虑风光不确定性对交易决策优化的影响。CVaR的值越高,决策的风险也就越大。为便于求解条件风险价值函数,对概率密度函数进行处理,量化由风光不确定性引起的调度风险。利用拉丁超立方抽样法模拟出s个场景,建立风险成本约束为
| $ \left\{\begin{array}{l} X_{\mathrm{CVaR}, \beta}=\alpha+\frac{1}{1-\beta} \sum\limits_{s=1}^s p_s[f(\xi, x)-\alpha]^{+} \\ {[f(\xi, x)-\alpha]^{+}=\max [f(\xi, x)-\alpha, 0]} \end{array}\right. $ | (21) |
式中:XCVaR,β,α——置信水平β下的CVaR成本和风险价值成本;
S——典型场景的数量;
ps——典型场景s的发生概率;
f(ξ,x)——随机变量ξ和调整后的决策变量x引起的风险损失函数。
根据式(21),考虑风险价值的目标函数为
| $ \begin{gathered} \min (1-k) \sum\limits_{s=1}^s f_{\mathrm{MMGA}}(s) p_s+k\left[\beta+\frac{1}{1-\alpha} \times\right. \\ \left.\sum\limits_{s=1}^s \max \left[f_{\mathrm{MMGA}}(s)-\beta, 0\right] p_s\right] \end{gathered} $ | (22) |
式中:fMMGA(s)——场景s是多微电网运营商运行成本;
k——风险因子,用于权衡经济效益与风险水平之间的关系。
3 模型求解方法
4 仿真分析
4.1 模型的经济性
为验证主从博弈下多微电网优化模型的经济性,选取某地多微电网系统为例进行仿真分析。对文献[14]的模型参数进行修改,3个微电网的场景如图 1所示。微电网中各设备运行参数见表 1。
表 1
微电网中各设备运行参数
| 参数 | 数值 | 参数 | 数值 | |
| 燃气轮机最大输出功率/kW | 350 | 燃气轮机效率 | 0.35 | |
| 燃气轮机最大输出热功率/kW | 450 | 微型燃气轮机热损失系数 | 0.07 | |
| 燃气锅炉最大输出热功率/kW | 400 | 燃气锅炉效率 | 0.9 | |
| 余热锅炉最大输出功率/kW | 450 | 余热锅炉热效率 | 0.76 | |
| 吸收式电制冷机最大输出功率/kW | 250 | 电制冷机制冷能效比 | 4 | |
| 电制冷机最大输出功率/kW | 350 | 吸收式电制冷机制冷效率 | 1.2 | |
| 储能最大充放电功率/kWh | 50 | 储能充放电效率数值 | 0.95 |
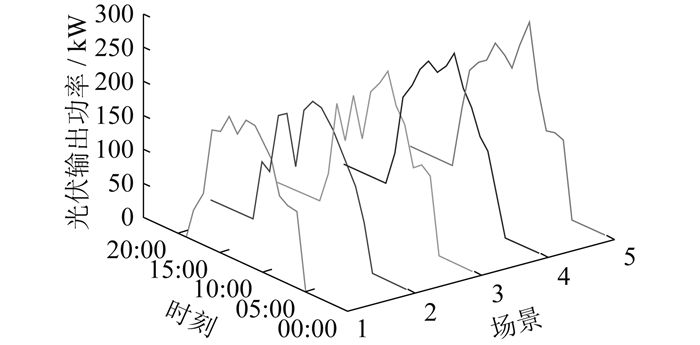
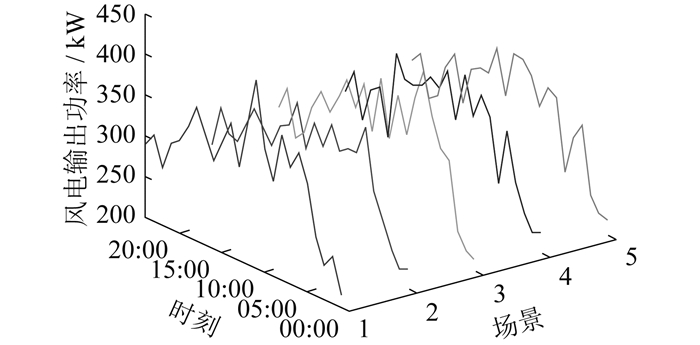
选取某地2022年春季风光输出功率数据,采用所提出的考虑风光不确定性和相关性的方法生成场景,采样规模为500。抽样及场景缩减后微电网典型日风电、光伏输出功率曲线如图 3、图 4所示。风光联合输出功率的5个场景概率分别为0.290、0.140、0.142、0.224和0.204。
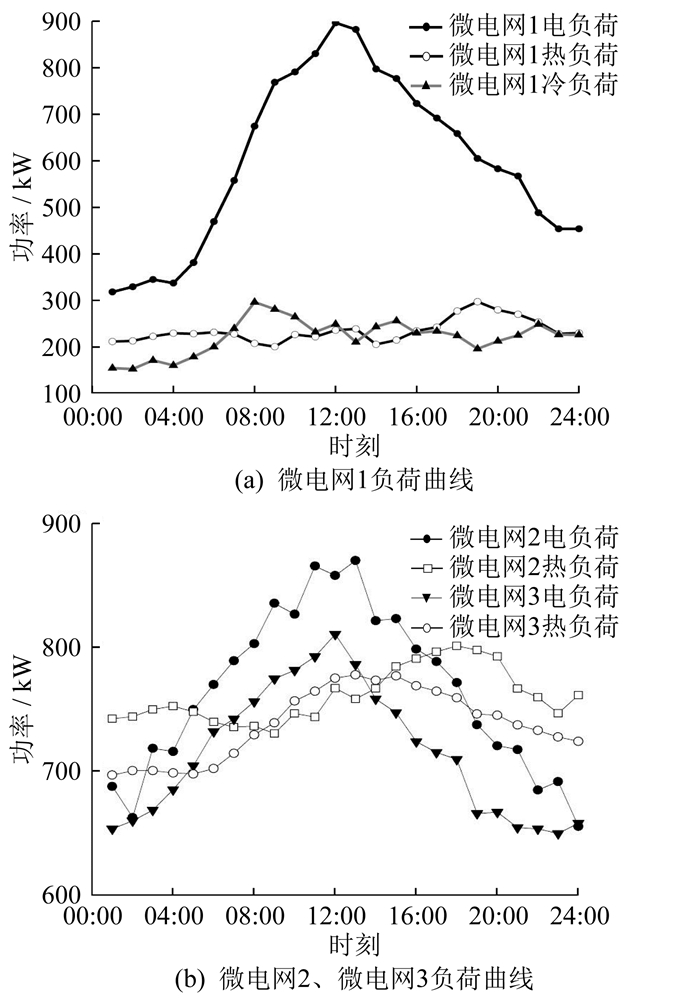
碳交易参数单位电量、热量的碳排放配额分别为0.798、0.385 kg/kWh,折算系数为1.9。弃风弃光惩罚系数为0.6元/kWh。各微电网负荷曲线如图 5所示。风险因子初始值设置为0.5。在MATLAB R2018b编译环境下,通过遗传算法对上层模型求解,种群数量为10,迭代次数为100,交叉因子为0.9,变异概率为5%。对下层模型采用CPLEX求解器进行求解。
设置3个场景进行分析验证。场景1:考虑风光不确定性,不考虑微电网之间的交互,独立运行,采用传统的多微电网优化模型,各微电网直接与上级电网进行交互。场景2:考虑主从博弈优化模型,不考虑风光不确定性,风光输出功率采用日前预测模型。场景3:考虑主从博弈优化模型和风光不确定性,即本文所用模型。不同场景下的成本分析如表 2所示。
表 2
不同算例的成本对比以及弃光率、弃风率对比
| 场景 | 成本/元 | 弃光率/% | 弃风率/% | |||
| 微电网1 | 微电网2 | 微电网3 | 多微电网 | |||
| 1 | 7 088.48 | 2 796.84 | 1 394.61 | 6 927.52 | 16.39 | 15.59 |
| 2 | 6 697.58 | 2 601.59 | 1 335.28 | 6 504.89 | 15.38 | 13.25 |
| 3 | 6 682.86 | 2 534.69 | 1 315.47 | 6 468.67 | 13.32 | 11.47 |
对比场景1和场景3可知:场景3考虑微电网之间的功率交互,微电网1~3的运行成本分别下降了5.72%、9.37%、5.67%,每个微电网的经济性得到提高,多微电网系统的运行成本也减少了458.85元。对比场景2和场景3可知:考虑风光不确定性有效降低了微电网运行成本,并且场景3比场景2的弃光率低2.06%、弃风率低1.78%。对比可得,考虑风光不确定性可以降低各微电网的成本并略微降低弃风弃光率。
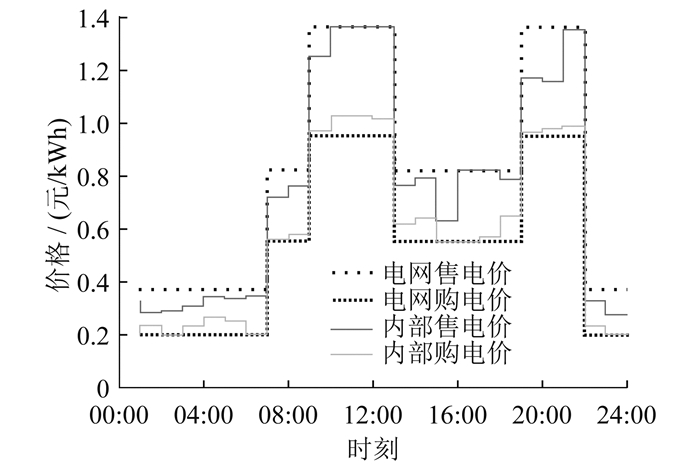
4.2 电价优化结果
根据本文制定的策略,多微电网运营商制定的内部电价如图 6所示。通过主从博弈,下级微电网之间的能源供需情况由上层多微电网运营商整体进行调度优化。电能的供需情况变化对电价有直接影响。内部的购售电价根据约束只能在电网购售价之间变动。内部购电价位于峰值是为了促进可再生能源消纳,减少向电网的购电,提升微电网的经济性。购电峰值之间出现下凹是因为此时电价高,但是微电网的负荷需求偏低,多微电网运营商通过降低交易价格可以降低各微电网的运行成本,并促进交易。
4.3 各微电网输出功率结果分析
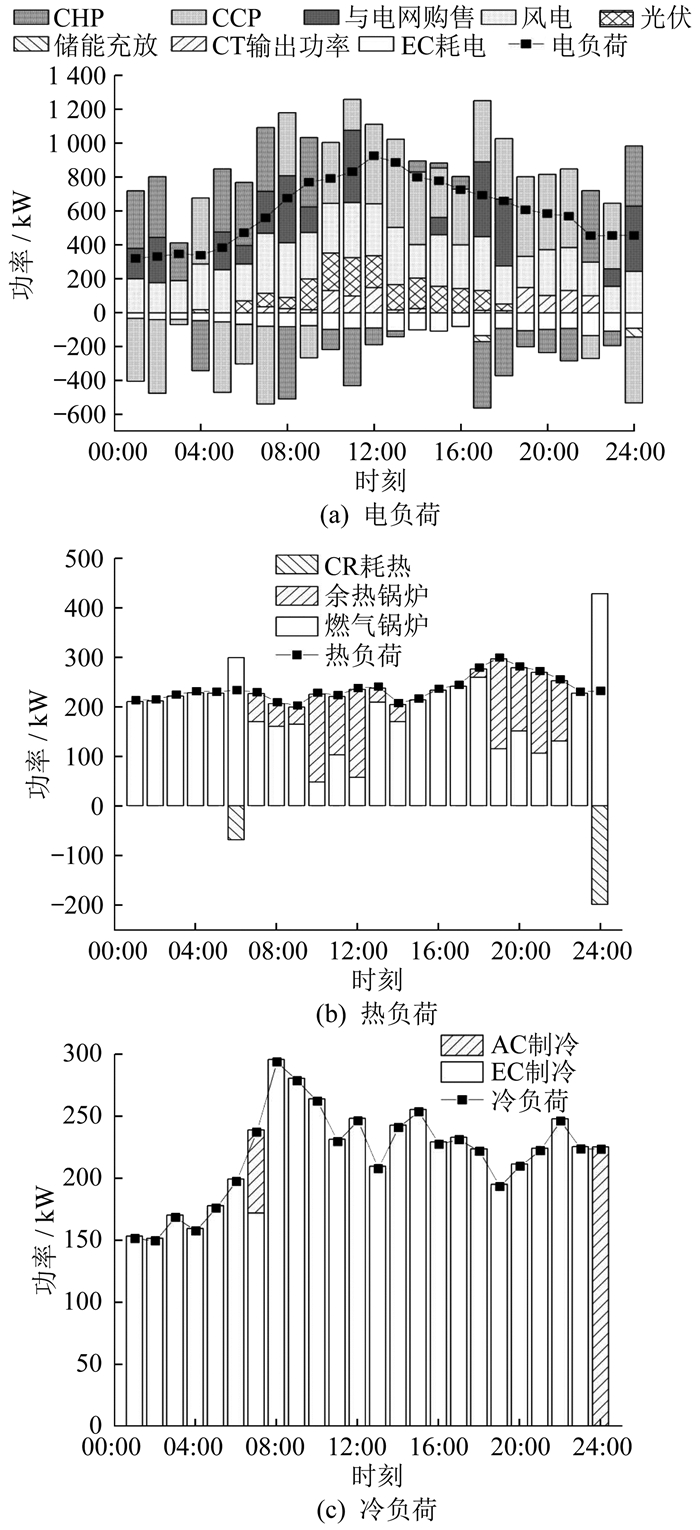
微电网1电、热、冷功率平衡如图 7所示。
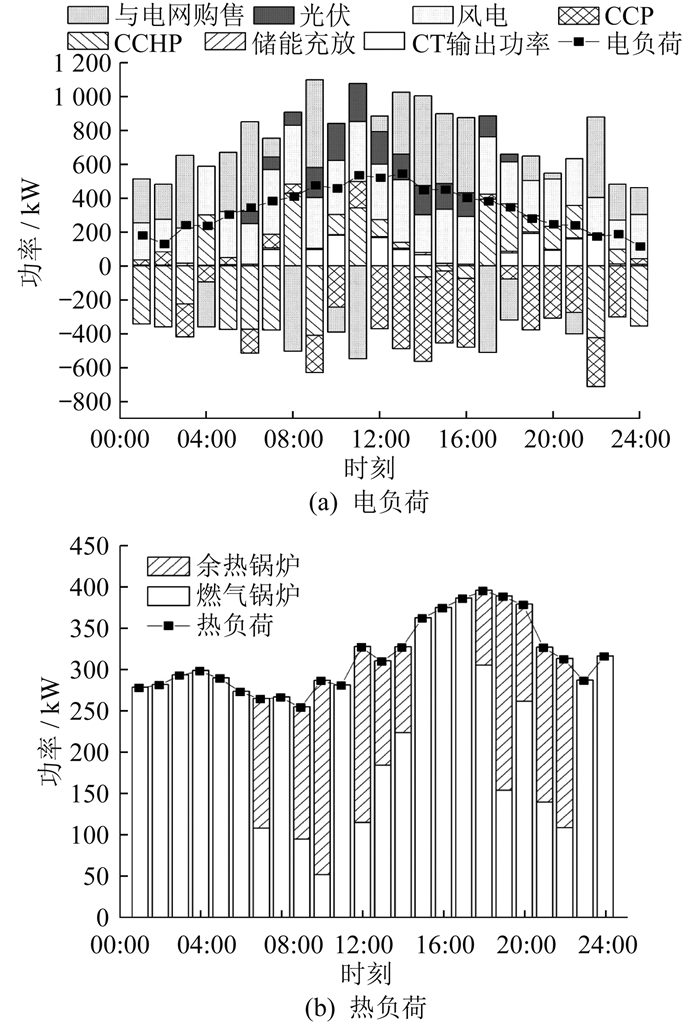
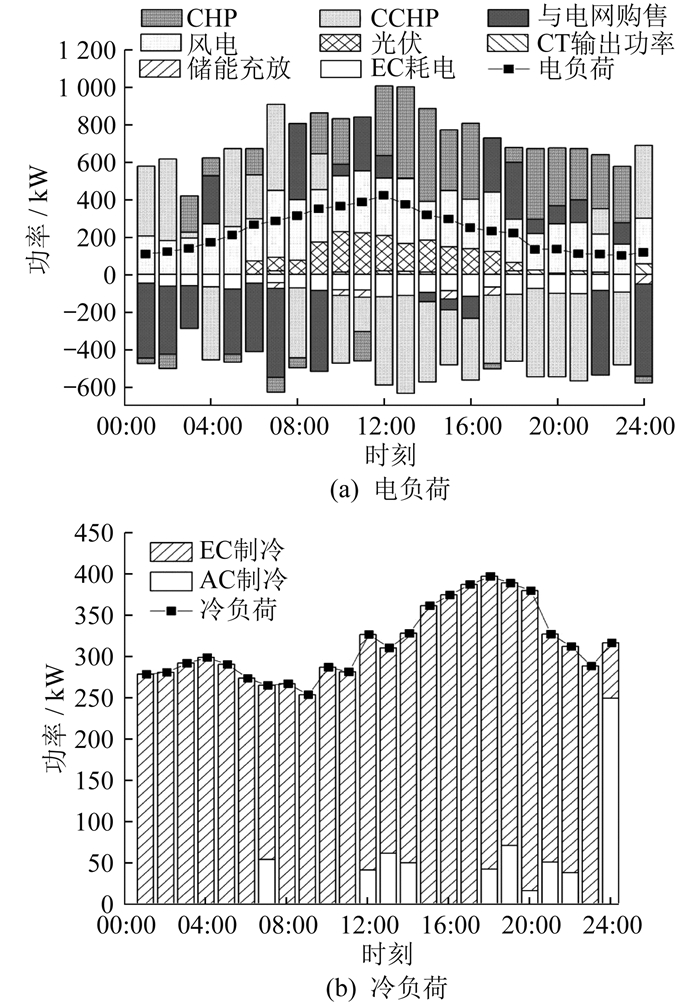
由图 7可知:微电网1为缺电型微电网,电负荷大于微电网1机组输出功率。为满足负荷需求,微电网1主要从上级电网和微电网2、3处购电来弥补功率缺额;微电网2、3的可再生能源输出功率比较充足,可以满足大部分时段的电力需求,其将多余的电能与微电网和电网进行交互可以降低自身运行成本,提高整个多微电网系统的经济性。微电网2电、热功率平衡如图 8所示。微电网3电、冷功率平衡如图 9所示。由图 7~图 9可知,3个微电网的热功率平衡,且主要由燃气锅炉提供。在电价高的时候,燃气轮机输出功率,提供热气给余热锅炉进行转换;而在电价低时,燃气轮机输出功率较少,主要通过燃气锅炉制热满足热负荷需求。冷负荷和热负荷的平衡原理相同,吸收式制冷机在电价低时无法从燃气轮机吸收热量制冷,可通过电制冷机满足冷负荷平衡。
4.4 碳交易价格分析
4.5 CVaR风险因素对多微电网成本的影响
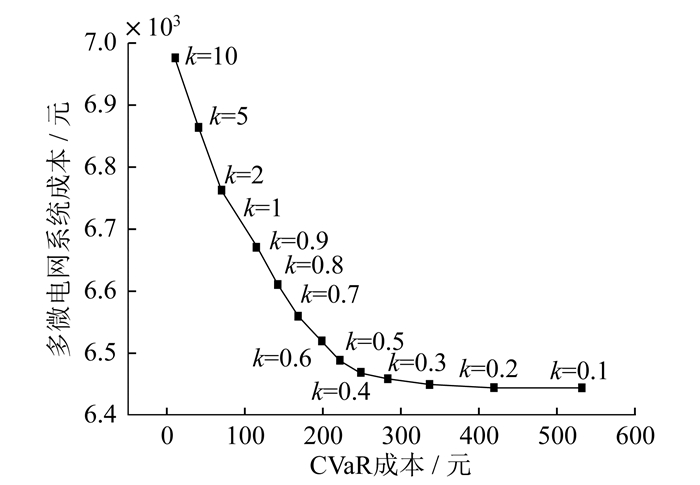
图 10展示了不同风险因子下多微电网系统成本与CVaR成本的关系。当风险因子k≤0.5时,风险因子对多微电网成本的影响几乎不变。随着风险因子增大,多微电网成本逐渐增加,且增加速度逐渐加快。这表示风险因子越大,风险估计越充分,风险损失越低,多微电网所承担的CVaR成本越低,但成本越高,经济性也越差。因此,多微电网的投资者可以通过选择合适的风险因子来衡量多微电网系统的风险性和经济性。
5 结语
本文研究了主从博弈下考虑风光不确定性的多微电网低碳优化模型。仿真结果显示:该模型提高了多微电网系统以及各微电网的经济性,提高了可再生能源的消纳率,减少了碳排放量。引入碳交易机制的多微电网协同运行有效降低了碳排放量,有助于实现“双碳”目标。采用CVaR量化风光不确定下多微电网系统面临风险损失时,通过选择合适的风险因子,可以更好地度量风险性和经济性。
参考文献
-
[1]周孝信, 陈树勇, 鲁宗相, 等. 能源转型中我国新一代电力系统的技术特征[J]. 中国电机工程学报, 2018, 38(7): 1893-1904.
-
[2]李晖, 刘栋, 姚丹阳. 面向碳达峰碳中和目标的我国电力系统发展研判[J]. 中国电机工程学报, 2021, 41(18): 6245-6259.
-
[3]ZHANG M, MU L, GUO W. New protection scheme for internal fault of multi-microgrid[J]. Protection and Control of Modern Power Systems, 2019, 4(2): 159-170.
-
[4]陈磊, 牛玉刚, 贾廷纲. 基于主从博弈的多微网能量调度策略[J]. 电力系统保护与控制, 2020, 48(19): 35-42.
-
[5]LIU N, HE L, YU X, et al. Multiparty energy management for grid-connected microgrids with heat-and electricitycoupled demand response[J]. IEEE Transactions Industrial Informatics, 2018, 14(5): 1887-1897. DOI:10.1109/TII.2017.2757443
-
[6]刘念, 赵璟, 王杰, 等. 基于合作博弈论的光伏微电网群交易模型[J]. 电工技术学报, 2018, 33(8): 1903-1910.
-
[7]帅轩越, 王秀丽, 吴雄, 等. 计及条件风险价值下基于合作博弈的多微网协同优化调度[J]. 电网技术, 2022, 46(1): 130-138.
-
[8]XU D, ZHOU B, LIU N, et al. Peer-to-peer multi-energy and communication resource trading for interconnected microgrids[J]. IEEE Transactions on Industrial Informatics, 2021, 17(4): 2522-2533. DOI:10.1109/TII.2020.3000906
-
[9]张宇威, 肖金星, 杨军, 等. 基于风光数据驱动不确定集合的配电网与多微网鲁棒经济调度[J]. 电力建设, 2021, 42(10): 40-50.
-
[10]邬嘉雨, 刘洋, 许立雄, 等. 区块链技术下考虑风电不确定性的微网群鲁棒博弈交易模式[J]. 电力建设, 2021, 42(9): 10-21.
-
[11]王俐英, 林嘉琳, 宋美琴, 等. 考虑需求响应激励机制的园区综合能源系统博弈优化调度[J]. 控制与决策, 2023, 38(11): 3192-3200.
-
[12]林顺富, 刘持涛, 李东东, 等. 考虑电能交互的冷热电区域多微网系统双层多场景协同优化配置[J]. 中国电机工程学报, 2020, 40(5): 1409-1421.
-
[13]王海洋, 李珂, 张承慧, 等. 基于主从博弈的社区综合能源系统分布式协同优化运行策略[J]. 中国电机工程学报, 2020, 40(17): 5435-5445.
-
[14]赵会茹, 陆昊, 李子衿, 等. 考虑风光不确定性的含储能CCHP微网市场环境下两阶段鲁棒优化运行策略[J]. 电力建设, 2020, 41(11): 116-125.