|
|
|
发布时间: 2024-10-28 |
智能电网技术 |
|
|
|
收稿日期: 2024-03-18
基金项目: 国家自然科学基金(51977127);上海市教育发展基金会和上海市教育委员会“曙光计划”(20SG52)
中图法分类号: TM734
文献标识码: A
文章编号: 2096-8299(2024)05-0439-10
|
摘要
高比例新能源接入电网,对电力系统的灵活调节能力提出了更高要求。提出了一种工业园区向上级电力系统提供爬坡服务的优化调度模型。首先,对风光不确定性进行处理生成典型场景,计算系统的灵活爬坡需求。然后,综合考虑调度成本与爬坡收益,以园区运行总成本最小为目标构建两阶段优化调度模型。最后,进行案例分析。结果显示:高载能负荷参与灵活爬坡服务后的园区收益较之前增加了57.01%,园区运行成本较高载能负荷未参与时降低了11.5%,有效提升了系统灵活性和降低了园区的运行成本。
关键词
高比例新能源; 高载能负荷; 灵活爬坡服务; 线性规划; 两阶段优化
Abstract
High proportion of new energy sources accessing the power grid puts higher requirements on the flexible regulation capability of the power system. In this paper, an optimal dispatch model for industrial parks is proposed to provide ramping services to the superior power system. Firstly, the wind and solar uncertainties are processed to generate a typical scenario to calculate the flexible ramping demand of the system. Then, the scheduling cost and ramping benefit are considered comprehensively to construct a two-phase optimal scheduling model with the objective of minimizing the total cost of the park operation. Finally, the case study is conducted and the results show that the revenue of the park after the participation of high-capacity loads in the flexible ramping service increased by 57.01% compared with the previous one, and the park operating cost decreased by 11.5% compared with the time when the high-capacity loads don't participate, which effectively improves the flexibility of the system and reduces the operating cost of the park.
Key words
high percentage of new energy sources; high energy-carrying loads; flexible ramping service; linear planning; two-stage optimization
“双碳”目标的提出,标志着我国在推动建设新型电力系统的道路上迈出了重要一步[1]。新能源发电比例的不断提高已成为我国电力行业发展的必然趋势,也是未来电力行业的重要特征。到2030年,新能源发电将占我国总发电量的30%以上,预计到2060年将达到60%[2]。然而,高比例新能源的接入不仅加大了系统净负荷的波动[3],还给电网的安全稳定运行带来了新挑战[4]。新能源的不确定性和间歇性特点使得电网调控难度增大,电网调控需要具备更高的灵活性和调节能力,因而对电力系统的调度能力提出了更高要求[5]。
电力系统灵活性是一种在不确定事故(新能源输出功率波动等)发生时通过调用可调节资源以应对相关时间尺度的供求变化来维持系统安全运行的能力[6]。为了应对未来可能会出现的能源不平衡现象,2014年,美国加州独立系统运营商和美国中西部电力运营商提出了一种灵活爬坡产品(Flexible Ramping Product,FRP)的概念[7]。FRP的主要作用是增强可调节资源的灵活性,以应对系统净负荷波动性变化导致的系统灵活性不足的情况。目前对FRP的研究主要集中在发电侧,以煤电为主的常规发电机组仍然是维持电网运行灵活性的主要来源。常规火电机组的部署是为了解决新能源发电输出功率份额较低时净负荷的波动问题。随着新能源发电占比的增加,一方面,新能源发电固有的间歇性和不确定性使得常规发电机组需要在调度中更频繁地调整其功率输出,有时甚至需要频繁地开关机[8],增加了机组的磨损。文献[9-10]通过综述当前电力市场中包含FRP的数学模型,提出了常规发电机组参与灵活爬坡市场的策略投标模型,但仅分析了依赖常规发电机组提供FRP会影响系统安全问题。另一方面,净负荷需求超出预期的偏差或急剧变化可能会导致在发电装机容量充足的情况下爬坡能力不足,从而导致限电或强制减载。随着系统对灵活性要求的提高,需求侧资源逐渐被纳入可调节资源的范围[11],现有研究将储能、电动汽车等能够跟随需求侧调度的资源纳入了提高系统灵活性研究的范围。储能系统由于具备快速启动和爬坡的优势而被广泛应用。文献[12]通过构建储能系统参与FRP市场的随机优化框架,证明了具有升压能力的储能系统在适当参与电力市场时可以提高其盈利能力和系统的灵活性。文献[13-14]研究了电动汽车参与灵活爬坡市场的情况,提出了一种将电动汽车作为灵活性资源的微电网调度模型。文献[15-16]提出了在实时阶段建立多阶段平衡模型,通过调用储能和火电机组共同提供FRP的方案,以解决系统灵活性不足的问题。以上研究大多聚焦于系统内部提供灵活性,但当系统内部灵活性不足时,只能考虑弃风弃光或者切除负荷,从而造成资源浪费,影响系统的稳定性。为解决这一问题,本文进一步考虑外部园区灵活性资源,向上级系统提供灵活爬坡服务,在提高园区运行经济性的同时也增加了系统的稳定性。
在工业园区风电集群接入的电网中,往往附近就建有大容量的高载能负荷。在各类可调负荷中,高载能负荷是一种柔性可控负荷,并且是电网中重要的需求侧资源。高载能负荷调节容量大、速度快、稳定性高,可以根据电网需求实现负荷的平稳调节以及平抑风光等新能源的波动,弥补常规机组在调节大规模风光波动方面的不足[17-18]。文献[19]提出了将高载能负荷作为可调节资源参与系统需求响应的优化调度模型,形成了源荷协调优化运行的调度模式。文献[20]针对自备电厂的可平移负荷,提出了高载能负荷参与需求响应的联合运行的多阶段模式,建立了含需求响应的机组组合模型。文献[21]具体分析了电熔镁负荷输出功率特性,建立了电熔镁负荷与常规机组共同参与的源荷协调优化模型,有效提高了新能源的消纳能力。上述文献说明,根据高载能负荷的响应特性,用直接负荷控制的方法让高载能负荷参与需求响应,可以有效消纳新能源、平抑净负荷波动,提高系统的经济性。
本文研究了高载能园区内可调节资源(储能和高载能负荷)共同向上级系统提供灵活爬坡服务的优化调度策略。该策略基于对不确定性场景的处理方法,对预测的风电光伏曲线进行了场景生成。以园区内运行总成本最小为目标,建立了日前-日内两阶段线性规划模型,对常规发电机组、储能系统和工业负荷等可调节资源进行了优化调度求解。通过对比分析北方某地工业园区的算例,验证了所提模型的合理性和有效性。
1 工业园区内的灵活爬坡服务
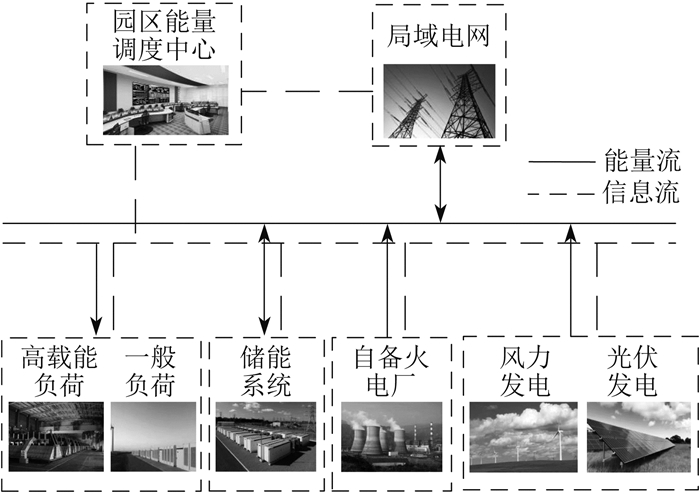
1.1 工业园区供电系统结构图
本文所介绍的工业园区供电系统结构图如 图 1所示,其内部主要包括自备火电厂、可再生能源(风电、光伏等)、储能系统以及园区内可调节负荷(高载能负荷等)。工业园区通过园区能量调度中心与上级局域电网进行信息与能量交互。
1.2 灵活爬坡服务的定义及计算
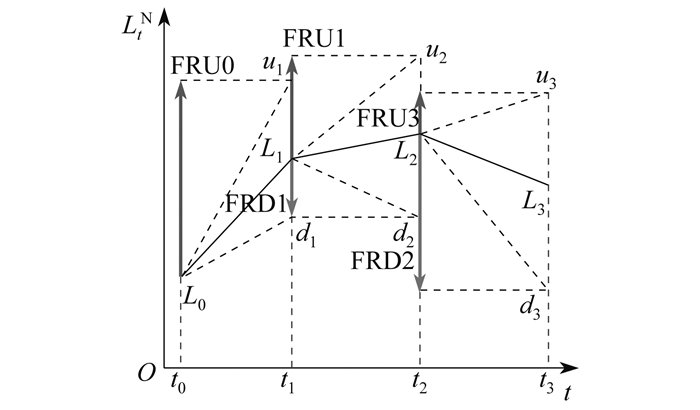
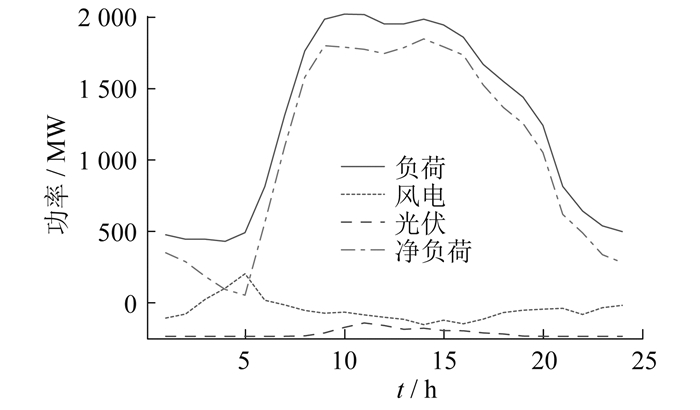
FRP作为新型辅助服务市场机制,被认为是一种提高系统灵活性的经济手段。在提升电力系统灵活性方面,FRP改善了系统的运行方式。实施FRP不需要投入新的电网设备或设施,且购买价格较低,是一种经济有效的系统灵活性提升措施。在考虑预测误差和可再生能源输出功率随机的情况下,FRP通过预留足够的灵活调节能力,确保系统能够满足下一个时段负荷变动需求,从而保持电力系统的实时平衡,提高系统的灵活性和经济性。FRP大致可分为两种类型:上行灵活爬坡服务(Uplink Flexible Ramping service,FRUs)和下行灵活爬坡服务(Downstream Flexible Ramping service,FRDs)[22]。灵活爬坡服务的需求由系统净负荷的向上波动和向下波动决定[23]。净负荷定义为系统总负荷与风电、光伏输出功率之差[24]。高比例新能源并网导致系统风电、光伏输出功率的随机性和波动性不断提高,系统的净负荷在一段时间内呈现出快速上升或下降的趋势[25],使得系统的稳定性下降。系统的新能源预测功率和净负荷曲线如图 2所示。
系统的灵活爬坡需求示意如图 3所示。FRUs主要用于应对系统负荷突然增加的情况,而FRDs则主要用于应对系统负荷突然减少的情况。L0、L1、L2、L3分别为对应时段系统预测的净负荷,系统净负荷的计算公式为
| $ L_{t}^{\mathrm{N}}=L_{t}-P_{t}^{\mathrm{PV}}-P_{t}^{\mathrm{WT}} $ | (1) |
式中:LtN——t时刻预测的系统净负荷功率;
Lt——t时刻预测的系统总负荷功率;
PtPV——t时刻预测的光伏功率;
PtWT——t时刻预测的风电功率。
图 3中,u1、u2、u3分别为净负荷在对应时间t时不确定性的上限;d1、d2、d3分别为净负荷在对应时间t时不确定性的下限。FRUs和FRDs的容量需求主要由以下两个方面决定:一是系统净负荷在当前和下一期之间的预测变化,二是为满足净负荷预测偏差量而产生的不确定性需求。表示为
| $ \left\{\begin{array}{l} P_{t}^{\mathrm{FRU}}=P_{t}^{\mathrm{U}}+U_{t}^{\mathrm{up}}\\ P_{t}^{\mathrm{FRD}}=P_{t}^{\mathrm{D}}+U_{t}^{\mathrm{dn}} \end{array}\right. $ | (2) |
式中:PtFRU——t时刻向上灵活爬坡的需求量;
PtFRD——t时刻向下灵活爬坡的需求量;
PtU——t时刻预测净负荷产生的上升需求量;
PtD——t时刻预测净负荷产生的下降需求量;
Utup——t时刻预留的向上安全裕度;
Utdn——t时刻预留的向下安全裕度。
| $ \left\{\begin{array}{l} P_{t}^{\mathrm{U}}=\max \left(0, \Delta L_{t}^{\mathrm{N}}\right) \\ P_{t}^{\mathrm{D}}=\min \left(0, \Delta L_{t}^{\mathrm{N}}\right) \\ \Delta L_{t}^{\mathrm{N}}=L_{t}^{\mathrm{N}}-L_{t-1}^{\mathrm{N}} \end{array}\right. $ | (3) |
式中:ΔLtN——两个连续时间段的净负荷变化。
1.3 工业园区风光不确定性场景生成
风电、光伏等分布式新能源的波动是不可避免的,新能源供应不足或者过剩都会影响园区的正常运行,从而对系统安全稳定运行造成影响。分析系统灵活性需求前首先要对风光输出功率的不确定性进行处理。通过引入风光不确定性场景,更真实地模拟实际情况,提高模型的可靠性。
风速概率密度函数通常采用服从两个参数的Weibull分布来描述,即
| $ f(v)=\left(\frac{k}{c}\right)\left(\frac{v}{c}\right)^{k-1} \exp \left[-\left(\frac{v}{c}\right)^{k}\right] $ | (4) |
式中:f(·)——概率密度函数;
v——实际风速;
c——Weibull分布的尺度参数;
k——Weibull分布的形状参数。
用Beta分布来精准地模拟光照强度的动态变化,其概率密度函数可以表示为
| $ f(r)=\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha) \Gamma(\beta)}\left(\frac{r}{r^{\max }}\right)^{\alpha-1}\left(1-\frac{r}{r^{\max }}\right)^{\beta-1} $ | (5) |
式中:r——t时刻光照强度;
rmax——光照强度最大值;
α,β——Beta分布的形状参数。
基于Copula函数建立风电和光伏场景生成的概率分布模型,具体步骤如下:
步骤1 基于某地风电、光伏历史功率数据,利用非参数核密度估计方法,选择高斯核函数,求解一天内(24 h)各时段(t=1,2,3,…,24,表示24个时段)风电、光伏功率的概率密度函数。
| $ \left\{\begin{array}{l} f\left(x_{t}^{\mathrm{WT}}\right)=\frac{1}{n h} \sum\limits_{d=1}^{n} K\left(\frac{x_{t}^{\mathrm{WT}}-X_{d, t}^{\mathrm{WT}}}{h}\right)\\ f\left(x_{t}^{\mathrm{PV}}\right)=\frac{1}{n h} \sum\limits_{d=1}^{n} K\left(\frac{x_{t}^{\mathrm{PV}}-X_{d, t}^{\mathrm{PV}}}{h}\right) \end{array}\right. $ | (6) |
式中:xtWT——t时刻风电功率;
n——总天数;
h——带宽;
K(·)——高斯核函数;
Xd,tWT——第d天t时刻风电功率;
xtPV——t时刻光伏功率;
Xd,tPV——第d天t时刻光伏功率。
步骤2 根据每个时段风电、光伏功率的概率密度函数,利用得到的Copula函数和边缘分布函数,建立每个时段的风电、光伏功率联合分布函数,即同时考虑了它们之间相关性的概率分布模型。
| $ F\left(x_{t}^{\mathrm{WT}}, x_{t}^{\mathrm{PV}}\right)=C\left[F_{\mathrm{wT}}\left(x_{t}^{\mathrm{WT}}\right), F_{\mathrm{PV}}\left(x_{t}^{\mathrm{PV}}\right)\right] $ | (7) |
式中:F(·)——概率分布模型;
C(·)——二维Copula函数;
FWT(·),FPV(·)——风电、光伏功率概率分布模型。
步骤3 根据生成的联合概率分布,对每个时段的风电、光伏功率进行采样模拟,求解生成每个时段对应的不同的风电和光伏功率情景。
| $ \left\{\begin{array}{c} x_{t}^{\mathrm{WT}}={F_{\mathrm{WT}}}^{-1}(u)=a_{d} u^{3}+b_{d} u^{2}+c_{d} u+l_{d} \\ x_{t}^{\mathrm{PV}}={F_{\mathrm{PV}}}^{-1}(v)=a_{d}^{\prime} v^{3}+b_{d}^{\prime} v^{2}+c_{d}^{\prime} v+l_{d}^{\prime} \end{array}\right. $ | (8) |
式中:u,v——累计采样概率值;
ad,bd,cd,ld——风电采样系数;
ad',bd',cd',ld'——光伏采样系数。
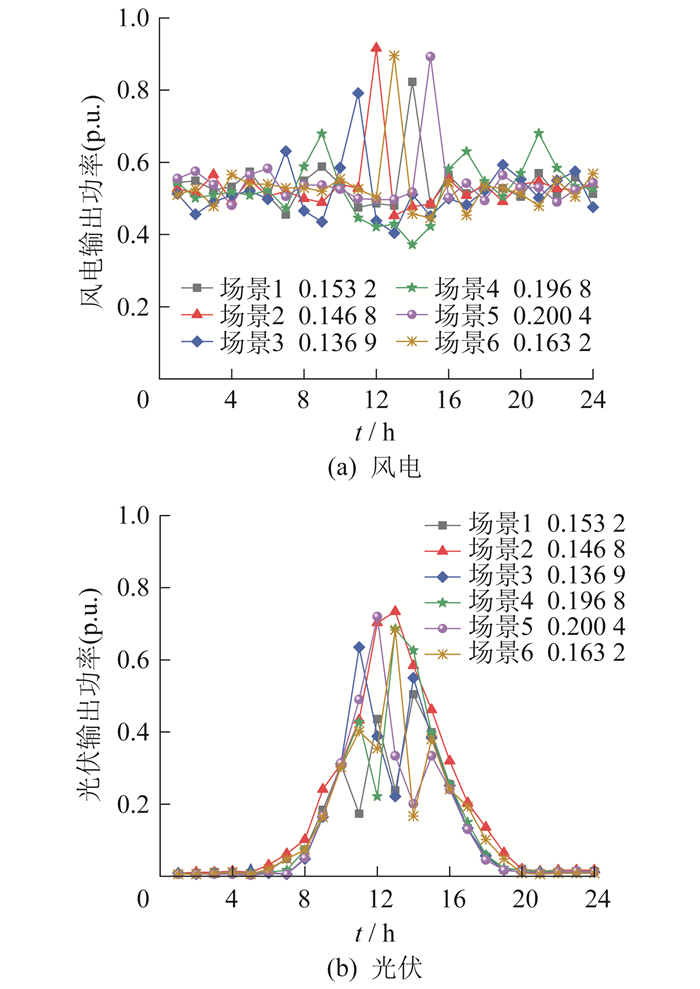
步骤4 采用基于改进K-means聚类的方法对采样样本进行场景削减,并计算各场景出现的概率。风电、光伏等新能源场景生成结果如图 4所示。
2 考虑灵活爬坡需求的系统日前日内优化调度模型
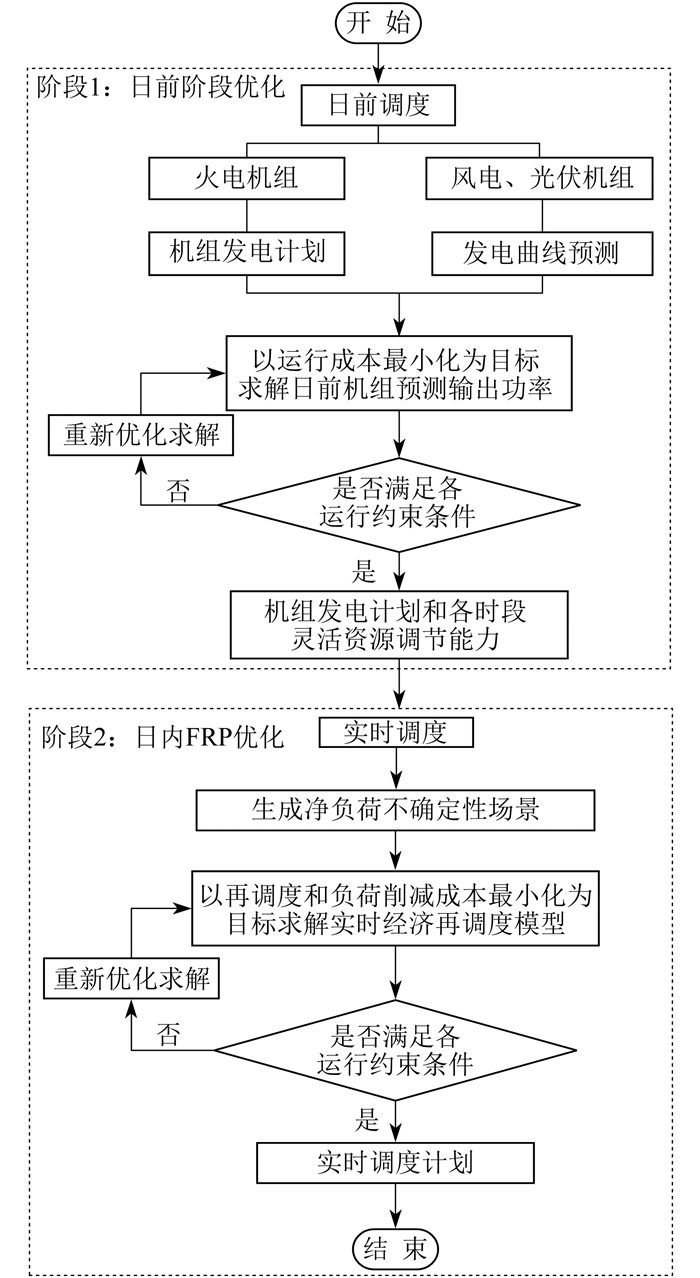
2.1 两阶段优化调度流程
基于本文所提出的工业园区向电力系统提供灵活爬坡服务的调度策略,利用工业园区特有的高载能负荷和储能系统协助常规火电机组共同作为园区内的可调节资源,以提高系统的灵活性;同时,以园区内运行总成本最小为目标,在工业园区内建立了考虑系统灵活爬坡需求的日前日内两阶段的混合整数线性规划调度模型。本文所提的两阶段优化调度流程如图 5所示。
第1阶段是日前阶段的优化调度模型,其时间尺度为1 h,每隔24 h进行一次调度;第2阶段是日内阶段的优化调度模型,其时间尺度为15 min,每隔15 min进行一次调度。阶段1确定下来的调度计划中的机组发电计划和高载能负荷生产计划会作为阶段2实时阶段调度的输入数据进行处理,阶段2对阶段1输出的园区日前调度计划中的可调节资源进行重新调度,求解得出火电机组和储能系统参与爬坡服务的实时输出功率。在不满足运行约束条件时,返回上一级重新进行优化求解,如果违反容量等约束条件,则产生弃风弃光或弃负荷等惩罚成本。不断地进行迭代比较,直至找到最优解,使园区运行成本最低。
2.2 阶段1:日前调度
2.2.1 阶段1目标函数
以工业园区内运行总成本最小作为日前调度的目标函数,包括能量成本、备用成本、FRP调用成本、弃风弃光成本以及向上级电网提供FRP的收益,表达式为
| $ f_{1}=\min \left(C^{\mathrm{ener}}+C^{1}+C^{\mathrm{fl}}+C^{\mathrm{rc}}-C^{\mathrm{frp}}\right) $ | (9) |
式中:f1——工业园区运行总成本;
Cener——能量成本;
Cl——备用成本;
Cf1——可调节资源调用成本;
Crc——弃风弃光惩罚成本;
Cfrp——园区向上级电网提供FRP的收益。
| $ \begin{align*} C^{\mathrm{ener}}= & \sum\limits_{t=1}^{N_{\mathrm{T}}} \sum\limits_{i=1}^{N_{\mathrm{G}}}\left[a_{i}\left(P_{i, t}^{\mathrm{g}}\right)^{2}+b_{i} P_{i, t}^{\mathrm{g}}+c_{i}\right]+ \\ & \sum\limits_{t=1}^{N_{\mathrm{T}}} \sum\limits_{i=1}^{N_{\mathrm{G}}} s_{i}\left(1-u_{i, t-1}\right) u_{i, t}+\sum\limits_{t} e_{0}\left(P_{t}^{\mathrm{ch}, \mathrm{bs}}+\right. \\ & \left.P_{t}^{\mathrm{dis}, \mathrm{bs}}\right)+\sum\limits_{t=1}^{N_{\mathrm{T}}} \sum\limits_{k=1}^{N_{\mathrm{H}}} \lambda_{k}^{\mathrm{h}} S_{k, t}^{\mathrm{h}} P_{k}^{\mathrm{h}}-\sum\limits_{t=1}^{T} \mu_{\mathrm{r}} P_{t}^{\mathrm{h}, \text { toal }} \end{align*} $ | (10) |
式中:NT——调度周期;
NG——常规火电发电机组数;
Pi,tg——t时刻火电机组i的功率;
ai,bi,ci——火电机组i的发电成本系数;
si——火电机组i的启停成本系数;
ui,t——t时刻火电机组i的运行状态;
e0——单位功率储能系统运行维护的成本系数;
Ptch,bs,Ptdis,bs——储能的充、放电功率;
NH——高载能负荷组数;
λkh——高载能负荷的单位调节成本;
Sk,th——t时刻高载能负荷的投切状态,Sk,th=0表示高载能负荷中断运行,Sk,th=1表示高载能负荷投入运行;
Pkh——高载能负荷的投切容量;
μr——风电、光伏新能源的上网价格;
Pth,total——高载能负荷的总投切能量。
| $ C^{1}=c^{1} \sum\limits_{\chi, t} \ell_{\gamma, t} $ | (11) |
式中:cl——备用成本系数;
χ——灵活性资源,包括常规火电机组、储能、高载能负荷;
ℓχ,t——灵活性资源χ在t时刻的备用分配。
| $ C^{\mathrm{fl}}=c^{\mathrm{p}} \sum\limits_{x, t}\left(f_{x, t}^{\mathrm{up}}+f_{x, t}^{\mathrm{dn}}\right) $ | (12) |
式中:cp——灵活性资源调用成本系数;
fχ,tup——t时刻灵活性资源χ的向上爬坡容量;
fχ,tdn——t时刻灵活性资源χ的向下爬坡容量。
| $ C^{\mathrm{rc}}=c^{\mathrm{PV}} \sum\limits_{t} P_{t}^{\mathrm{PV}, \mathrm{rc}}+c^{\mathrm{WT}} \sum\limits_{t} P_{t}^{\mathrm{WT}, \mathrm{rc}} $ | (13) |
式中:cPV——单位弃光惩罚成本系数;
cWT——单位弃风惩罚成本系数;
PtPV,rc——t时刻的弃光量;
PtWT,rc——t时刻的弃风量。
| $ C^{\mathrm{frp}}=c^{\mathrm{frp}} \sum\limits_{t}\left(P_{t}^{\mathrm{FRU}}+P_{t}^{\mathrm{FRD}}\right) $ | (14) |
| $ P_{t}^{\mathrm{FRU}}=\sum\limits_{i, e, k}\left(f_{i, t}^{\mathrm{g}, \mathrm{up}}+f_{e, t}^{\mathrm{up}}+f_{k, t}^{\mathrm{h}, \mathrm{up}}\right) $ | (15) |
| $ P_{t}^{\mathrm{FRD}}=\sum\limits_{i, e, k}\left(f_{i, t}^{\mathrm{g}, \mathrm{dn}}+f_{e, t}^{\mathrm{dn}}+f_{k, t}^{\mathrm{h}, \mathrm{dn}}\right) $ | (16) |
式中:cfrp——向上级电网提供FRP的价格;
fi,tg,up,fi,tg,dn——t时刻火电机组i向上、向下爬坡容量;
fe,tup,fe,tdn——t时刻储能e向上、向下爬坡容量;
fk,th,up,fk,th,dn——t时刻高载能负荷k向上、向下爬坡容量。
2.2.2 阶段1约束条件
(1)火电机组约束条件。火电机组约束方程可以表示为
| $ P_{i, t}^{\mathrm{g}}+\ell_{i, t}^{\mathrm{g}}+f_{i, t}^{\mathrm{g}, \mathrm{up}} \geqslant P_{i}^{\mathrm{g}, \max } u_{i, t} $ | (17) |
| $ P_{i, t}^{\mathrm{g}}-\ell_{i, t}^{\mathrm{g}}-f_{i, t}^{\mathrm{g}, \mathrm{dn}} \geqslant P_{i}^{g, \min } u_{i, t} $ | (18) |
| $ P_{i, t}^{\mathrm{g}}-P_{i, t-1}^{\mathrm{g}}+\ell_{i, t}^{\mathrm{g}}+f_{i, t}^{\mathrm{g}, \mathrm{up}}+f_{i, t-1}^{\mathrm{g}, \mathrm{dn}} \leqslant t R_{i}^{\mathrm{g}, \mathrm{up}} u_{i, t-1}+t R_{i}^{\mathrm{g}, \mathrm{st}} v_{i, t} $ | (19) |
| $ P_{i, t-1}^{\mathrm{g}}-P_{i, t}^{\mathrm{g}}+f_{i, t}^{\mathrm{g}, \mathrm{dn}}+f_{i, t-1}^{\mathrm{g}, \mathrm{up}} \leqslant t R_{i}^{\mathrm{g}, \mathrm{dn}} u_{i, t}+t R_{i}^{\mathrm{g}, \mathrm{sd}} v_{i, t} $ | (20) |
式中:Pi,tg——t时刻火电机组i的有功功率;
ℓi,tg——t时刻光电机组i备用容量;
Pig,max——火电机组i的有功功率上限;
Pig,min——火电机组i的有功功率下限;
Rig,up——火电机组i向上爬坡极限;
Rig,dn——火电机组i向下爬坡极限;
Rig,st——火电机组i爬坡开始极限;
Rig,sd——火电机组i爬坡结束极限。
(2)储能系统约束条件。储能设备的约束方程可以表示为
| $ E_{e, t}=E_{e, t-1}+\left[\left(P_{t}^{\mathrm{dis}, \mathrm{bs}}+f_{e, t}^{\mathrm{dn}}\right) \eta^{\mathrm{dis}}-\frac{\left(P_{t}^{\mathrm{ch}, \mathrm{bs}}+f_{e, t}^{\mathrm{up}}\right)}{\eta^{\mathrm{ch}}}\right] \Delta t $ | (21) |
| $ P_{t}^{\mathrm{ch}, \mathrm{bs}}+f_{e, t}^{\mathrm{dn}} \leqslant P^{\mathrm{ch}, \max } u_{t}^{\mathrm{ch}} $ | (22) |
| $ P_{t}^{\mathrm{dis}, \mathrm{bs}}+f_{e, t}^{\mathrm{up}} \leqslant P^{\mathrm{dis}, \max } u_{t}^{\mathrm{dis}} $ | (23) |
| $ u_{t}^{\mathrm{ch}}+u_{t}^{\mathrm{dis}} \leq 1 $ | (24) |
式中:Ee,t——t时刻储能设备e的荷电状态;
P ch,max——储能设备充电上限;
P dis,max——储能设备放电上限;
utch,utdis——t时刻储能设备充、放电工作状态的0-1变量;
ηch,ηdis——储能设备充、放电效率。
(3)高载能负荷调度约束条件。高载能负荷调度约束方程可以表示为
| $ \begin{align*} & \left\{\begin{array}{c} 0 \leqslant P_{k, t}^{\mathrm{h}}+f_{t}^{\mathrm{h}, \text {up }} \leqslant S_{k, t}^{\mathrm{h}} P_{k}^{\mathrm{h}, \text { max }} \\ P_{k, t}^{\mathrm{h}}-f_{t}^{\mathrm{h}, \mathrm{dn}} \geqslant S_{k, t}^{\mathrm{h}} P_{k}^{\mathrm{h}, \text { min }} \end{array}\right. \end{align*} $ | (25) |
| $ \begin{align*} \left\{\begin{array}{c} P_{k, t}^{\mathrm{h}}-P_{k, t-1}^{\mathrm{h}} \leqslant S_{k, t-1}^{\mathrm{h}} P_{k}^{\mathrm{h}, \text { up }}+\left(1-S_{k, t-1}^{\mathrm{h}}\right) P_{k}^{\mathrm{h}, \text { max }} \\ P_{k, t-1}^{\mathrm{h}}-P_{k, t}^{\mathrm{h}} \leqslant S_{k, t}^{\mathrm{h}} P_{k}^{\mathrm{h}, \mathrm{dn}}+\left(1-S_{k, t}^{\mathrm{h}}\right) P_{k}^{\mathrm{h}, \max } \end{array}\right. \end{align*} $ | (26) |
| $ 0 \leqslant \sum\limits_{\tau=1}^{T}\left|S_{k}^{\mathrm{h}}(\tau)-S_{k}^{\mathrm{h}}(\tau-1)\right| \leqslant M $ | (27) |
式中:Pkh,max,Pkh,min——高载能负荷最大和最小功率;
Pkh,up,Pkh,dn——高载能负荷上、下投切限值;
M——高载能负荷投切限值。
(4)系统备用容量约束条件。系统的旋转备用约束方程可以表示为
| $ \ell_{t}^{\mathrm{req}} \leqslant \sum\limits_{i, t}\left(\ell_{i, t}^{\mathrm{g}}\right) $ | (28) |
| $ \ell_{t}^{\mathrm{req}}=50 \% \max \left\{0.05 \sum L_{t}, \max \left(P_{\chi}^{\max }\right)\right\} $ | (29) |
式中:ℓtreq——t时刻系统的旋转备用容量;
Pχmax——系统灵活性资源χ的最大功率。
(5)系统功率平衡约束条件。功率平衡约束方程可以表示为
| $ P_{t}^{\text {load }}+P_{t}^{\mathrm{ch}, \mathrm{bs}}=P_{t}^{\mathrm{PV}}+P_{t}^{\mathrm{WT}}+P_{i, t}^{\mathrm{g}}+P_{t}^{\mathrm{dis}, \mathrm{bs}}+P_{k, t}^{\mathrm{h}, \mathrm{up}}+P_{k, t}^{\mathrm{h}, \mathrm{dn}} $ | (30) |
2.3 阶段2:日内调度
阶段2的目标函数是在日内调度中园区内负荷削减惩罚成本和FRP再调用成本之和达到最小,可表示为
| $ f_{2}=\min \left(C^{\mathrm{LC}}+C^{\mathrm{f} 2}\right) $ | (31) |
式中:CLC——日内调度中的负荷削减成本;
Cf2——日内调度中的FRP再调用成本。
| $ C^{\mathrm{LC}}=\sum c^{\mathrm{cut}} P_{t}^{\mathrm{cut}} $ | (32) |
式中:ccut——负荷削减惩罚成本系数;
Ptcut——t时刻的负荷削减量。
| $ C^{\mathrm{f} 2}=\sum\limits_{\chi \notin k, t} c^{\mathrm{f} 2}\left(f_{\chi \notin k, t}^{\mathrm{up}}+f_{\chi \notin k, t}^{\mathrm{dn}}\right) $ | (33) |
式中:cf2——可调节资源日内调用成本;
fχ∉k,tup——日内调度中可调节资源χ在t时刻调用的FRU;
fχ∉k,tdn——日内调度中可调节资源χ在t时刻调用的FRD。
日内调度中,高载能负荷由于投入和中断需要一段连续稳定时间,并且在短时间内多次投切会造成资源调用成本过高,破坏系统的经济性,故不考虑作为灵活性资源进行调度。
日内调度的系统灵活爬坡需求计算可以表示为
| $ N_{t}^{\mathrm{RT}-\mathrm{up}}=\max \left(0, \beta_{t}^{\mathrm{RT}}-\beta_{t}^{\mathrm{RT}}\right) $ | (34) |
| $ N_{t}^{\mathrm{RT}-\mathrm{dn}}=\max \left(0, \beta_{t-1}^{R T}-\beta_{t}^{\mathrm{RT}}\right) $ | (35) |
式中:NtRT-up——实时调度中t时刻系统的向上爬坡需求;
NtRT-dn——实时调度中t时刻系统的向下爬坡需求;
βtRT——t时刻预测的系统净负荷。
日内调度中的其他约束条件与日前调度相同。
3 算例与结果分析
3.1 算例介绍
为验证模型的有效性,以我国内蒙古自治区某经济循环工业园区为算例进行验证。该工业园区的供电系统包含总容量为450 MW的风电场、总容量为100 MW的光伏电厂、10台火电机组,以及储能系统和高载能负荷,具体参数参考内蒙古自治区落地项目。高载能负荷的主要参数和储能系统的主要参数如表 1、表 2所示。常规机组的运行参数如表 3所示。典型日风电、光伏和净负荷输出功率曲线如图 6所示。所提出的混合整数线性规划模型在MATLAB 2019中使用CPLEX求解,计算机配置为Intel Core i7-10510U系列,主频1.8 GHz,内存16 GB。
表 1
高载能负荷主要参数
| 高载能负荷参数 | 数值 |
| 上投切限值/MW | 20 |
| 下投切限值/MW | 20 |
| 最大功率/MW | 63 |
| 最小功率/MW | 40 |
| 额定功率/MW | 60 |
| 投切次数/次 | 20 |
表 2
储能系统主要参数
| 储能参数 | 数值 |
| 充电功率上下限/MW | 100 |
| 放电功率上下限/MW | 100 |
| 充电效率/% | 95 |
| 放电效率/% | 95 |
| 额定容量/MW | 200 |
| 容量上限/MW | 150 |
| 容量下限/MW | 50 |
表 3
常规机组运行参数
| 机组i | 最大功率/ MW |
最小功率/ MW |
爬坡率/ (MW/h) |
机组运行成本系数 | 容量备用成本/ (元/MWh) |
额定容量/ MW |
||
| ai | bi | ci | ||||||
| 1 | 90 | 20 | 45 | 0.002 | 23 | 250 | 12.1 | 100 |
| 2 | 90 | 20 | 45 | 0.002 | 23 | 250 | 11.8 | 100 |
| 3 | 180 | 50 | 60 | 0.002 | 23 | 300 | 12.5 | 200 |
| 4 | 180 | 50 | 60 | 0.002 | 23 | 300 | 15.3 | 200 |
| 5 | 280 | 60 | 100 | 0.002 | 22 | 700 | 11.2 | 300 |
| 6 | 280 | 60 | 100 | 0.002 | 22 | 700 | 15.1 | 300 |
| 7 | 335 | 80 | 100 | 0.002 | 23 | 400 | 13.4 | 350 |
| 8 | 335 | 80 | 100 | 0.002 | 23 | 400 | 10.3 | 350 |
| 9 | 375 | 100 | 100 | 0.002 | 23 | 400 | 13.6 | 400 |
| 10 | 375 | 100 | 100 | 0.002 | 23 | 400 | 12.8 | 400 |
3.2 3种方案对比分析
为验证所提方法、模型的可行性和优势,采用3种方案进行对比分析。
方案1 仅由传统的火电机组提供FRP。
方案2 由传统的火电机组和储能共同提供FRP。
方案3 由传统的火电机组、储能和工业园区内的高载能负荷共同提供FRP。
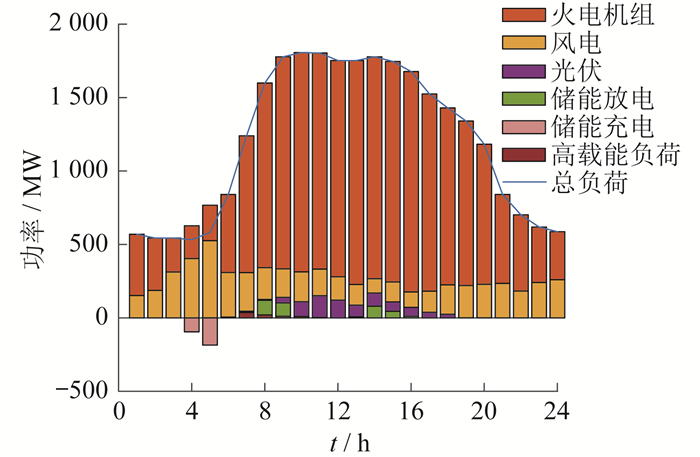
园区内功率平衡图如图 7所示。
3种方案的成本比较如表 4所示。
表 4
3种方案成本比较
| 方案 | 能量成本 | 备用成本 | 弃风弃光成本 | FRP收益 | 负荷削减成本 | 总成本 |
| 1 | 68.347 | 2.748 | 8.764 | 1.668 | 3.489 | 88.696 |
| 2 | 65.955 | 1.639 | 4.152 | 2.348 | 3.076 | 78.306 |
| 3 | 64.960 | 1.438 | 0 | 3.880 | 1.968 | 69.298 |
由表 4可知,工业园区灵活性资源参与FRP可以获得一定的收益。方案2和方案3与方案1对比,所获得的收益分别增加了28.96% 和57.01%。方案1、方案2、方案3场景的弃风弃光量依次降低,方案2和方案3分别比方案1降低了52.6% 和100%。方案2运行总成本比方案1降低了11.71%,方案3比方案2的运行总成本降低了11.50%。方案3、方案2、方案1场景对新能源发电的利用率依次增大。综上所述,在工业园区内利用高载能负荷参与灵活爬坡服务可以进一步提高FRP的收益,降低园区成本,减少弃风、弃光量。同时,共同利用多种可调节资源参与灵活爬坡服务,系统可以调用的FRP增加,能有效降低灵活性资源调用成本并获得FRP收益,从而降低园区能量成本,提高了系统的灵活性。
两种风光典型场景下园区运行总成本比较如表 5所示。
表 5
两种风光典型场景下园区运行总成本比较
| 方案 | 运行总成本 | |
| 新能源波动较剧烈时 | 新能源波动较平缓时 | |
| 1 | 90.462 | 88.696 |
| 2 | 80.765 | 78.306 |
| 3 | 69.925 | 69.298 |
两个场景分别为新能源波动较平缓和较剧烈的情况。在新能源波动较为平缓的场景下,方案2运行总成本比方案1降低了11.71%,方案3运行总成本比方案2降低了11.50%。在新能源波动较剧烈的场景下,方案2运行总成本较方案1降低了10.72%;方案3运行总成本比方案2降低了13.42%。在高比例新能源介入下,在工业园区内利用高载能负荷参与灵活爬坡服务更适用于系统波动频繁的情况,可以提高系统的灵活性,维持系统稳定运行。
3.3 两阶段灵活性资源调度方案
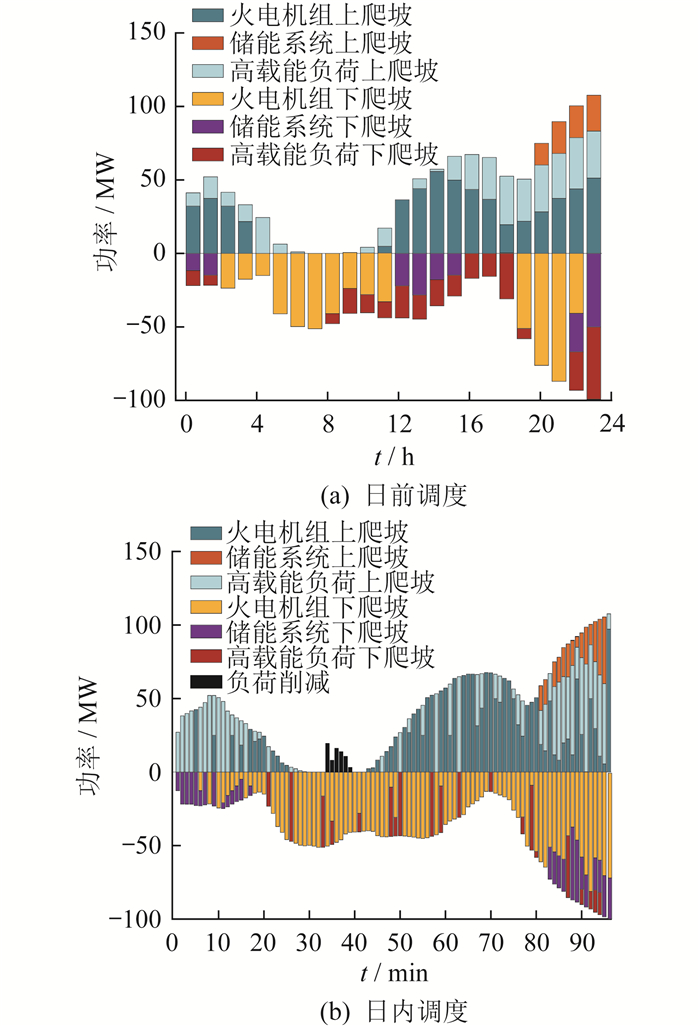
在实时调度区间内,当净负荷波动超过预测的不确定性区间时,系统的向上灵活爬坡需求超过了系统可提供的调节能力,即系统的可调节资源已经耗尽。此时,园区提供的灵活性不足,需要削减负荷以维持系统平衡。在实时阶段对园区内灵活性资源进行再调度处理,可以进一步优化灵活爬坡服务,降低净负荷预测的误差对系统安全运行的影响,减少系统内负荷削减量,降低惩罚成本,从而降低系统运行成本,提高园区整体运行的经济性。园区FRP优化调度示意如图 8所示。
由图 8可知,与方案1和方案2相比,在方案3下,常规火电机组、储能系统和高载能负荷共同参与FRP,可调用的FRPs和FRDs明显增加,园区向上、向下爬坡能力更强,应对新能源波动性的调节能力也更强,系统切负荷明显减少,系统的灵活性更高,稳定性更强。
4 结语
针对工业园区背景,考虑系统灵活性需求,研究了园区内火电机组、储能系统和高载能负荷共同提供系统灵活爬坡服务的优化调度模型。为合理调度园区内的可调节资源,进而为系统灵活爬坡服务提供可靠依据,对多种可调节资源参与系统灵活爬坡服务对园区运行总成本的影响进行了分析。研究结果表明:工业园区的高载能负荷可以通过灵活调整用电模式的方式参与系统灵活爬坡服务,实现与上级系统的供需匹配。相比于仅有传统火电机组和储能系统参与的情况,高载能负荷的参与能够有效降低系统的弃风、弃光成本,降低系统失负荷的风险,从而进一步提高能源的利用率。工业园区向上级系统提供的灵活爬坡服务有助于提高电力系统的运行稳定性,降低系统的运行风险,保障了电力系统的安全稳定运行。工业园区通过参与系统的灵活爬坡服务,不仅可以获得一定的经济补偿,降低园区的运行成本,还促进了清洁能源的消纳,实现了一定的环保效益,推动了可持续发展。下一步拟在考虑潮流对系统影响下进一步研究分时电价对工业园区灵活性资源参与系统爬坡服务的影响。
参考文献
-
[1]卓振宇, 张宁, 谢小荣, 等. 高比例可再生能源电力系统关键技术及发展挑战[J]. 电力系统自动化, 2021, 45(9): 171-191.
-
[2]ZHAO Y. Real-time dispatch of flexible ramping products for energy storage and demand response[C]//2019 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia). Chengdu, China: IEEE, 2019: 1936-1941.
-
[3]EL-KAREEM A A H, ELHAMEED M A, ELKHOLY M. Effective damping of local low frequency oscillations in power systems integrated with bulk PV generation[J]. Protection and Control of Modern Power Systems, 2021, 6(1): 41. DOI:10.1186/s41601-021-00219-6
-
[4]陈璨, 樊小伟, 张文浩, 等. 促进分布式光伏消纳的两阶段源网荷储互动优化运行策略[J]. 电网技术, 2022, 46(10): 3786-3799.
-
[5]LI Y, DENG Y, WANG Y, et al. Robust bidding strategy for multi-energy virtual power plant in peak-regulation ancillary service market considering uncertainties[J]. International Journal of Electrical Power & Energy Systems, 2023, 151: 109101.
-
[6]International Energy Agency. Harnessing variable renewables: a guide to the balancing challenge[R]. [S. l. ]: International Energy Agency, 2019.
-
[7]CRAIG M T, JARAMILLO P, HODGE B M, et al. Compounding climate change impacts during high stress periods for a high wind and solar power system in Texas[J]. Environmental Research Letters, 2020, 15(2): 024002. DOI:10.1088/1748-9326/ab6615
-
[8]GUO H, CHEN Q, XIA Q, et al. Flexible ramping product in electricity markets: basic concept equilibrium modeland research prospect[J]. Proceedings of the CSEE, 2017, 37(11): 3057-3066.
-
[9]马洪艳, 贠靖洋, 严正. 基于分布鲁棒优化的灵活爬坡备用调度方法[J]. 中国电机工程学报, 2020, 40(19): 6121-6132.
-
[10]KHOSHJAHAN M, MOEINI-AGHTAIE M, FOTUHIFIRUZABAD M, et al. Advanced bidding strategy for participation of energy storage systems in joint energy and flexible ramping product market[J]. IET Generation Transmission & Distribution, 2020, 14(22): 5202-5210.
-
[11]邓倩文, 李奇, 邱宜彬, 等. 考虑多类型灵活性资源联合运行的综合能源系统优化配置方法[J/OL]. 上海交通大学学报: 1-24[2024-02-15]. https://xuebao.sjtu.edu.cn/CN/10.16183/j.cnki.jsjtu.2023.457.
-
[12]KIM D, KWON K B, KIM M K. Application of flexible ramping products with allocation rates in microgrid utilizing electric vehicles[J]. International Journal of Electrical Power & Energy Systems, 2021, 133(2): 107340.
-
[13]ZHANG B, KEZUNOVIC M. Impact on power system flexibility by electric vehicle participation in ramp market[J]. IEEE Transactions on Smart Grid, 2015, 7(3): 1285-1294.
-
[14]GHALJEHEI M, KHORSAND M. Day-ahead operational scheduling with enhanced flexible ramping product: design and analysis[J]. IEEE Transactions on Power Systems, 2021, 37: 1842-1856.
-
[15]BAGHERI A, KHATAMI R, PARVANIA M. Continuoustime look-ahead flexible ramp scheduling in real-time operation[J]. International Journal of Electrical Power & Energy Systems, 2020, 119: 105895.
-
[16]初壮, 赵蕾, 孙健浩, 等. 考虑热能动态平衡的含氢储能的综合能源系统热电优化[J]. 电力系统保护与控制, 2023, 51(3): 1-12.
-
[17]于飞, 葛思伟, 李梅航, 等. 工业园区微网调度研究与仿真[J]. 电力系统保护与控制, 2023, 51(18): 179-187.
-
[18]HAO H, CORBIN C D, KALSI K, et al. Transactive control of commercial buildings for demand response[J]. IEEE Transactions on Power Systems, 2017, 32(1): 774-783. DOI:10.1109/TPWRS.2016.2559485
-
[19]熊伟, 马志程, 张晓英, 等. 计及风、光消纳的风电-光伏-光热互补发电二层优化调度[J]. 太阳能学报, 2022, 43(7): 39-48. DOI:10.19912/j.0254-0096.tynxb.2020-1146
-
[20]王健, 鲁宗相, 乔颖, 等. 高载能负荷提高风电就地消纳的需求响应模式研究[J]. 电网技术, 2017, 41(7): 2115-2124. DOI:10.13335/j.1000-3673.pst.2016.2467
-
[21]张海亮, 王艺博, 蔡国伟, 等. 面向风电消纳与电熔镁高载能负荷调控的源荷协调优化策略[J]. 电工技术学报, 2022, 37(17): 4401-4410.
-
[22]江涵, 岳程燕, 严兴煜, 等. 高比例可再生能源系统惯量约束对灵活性分析的影响研究[J]. 电力系统保护与控制, 2021, 49(18): 44-51. DOI:10.19783/j.cnki.pspc.201381
-
[23]郭鸿业, 陈启鑫, 夏清, 等. 电力市场中的灵活调节服务: 基本概念、均衡模型与研究方向[J]. 中国电机工程学报, 2017, 37(11): 3057-3066. DOI:10.13334/j.0258-8013.pcsee.162369
-
[24]张景淳, 陈胜, 彭琰, 等. 计及灵活爬坡的气-电耦合综合能源系统低碳经济调度研究[J]. 电网技术, 2022, 46(9): 3315-3325.
-
[25]GHAEMI S, SALEHI J, MOEINI-AGHTAIE M. Estimating abilities of distributed energy resources in providing flexible ramp products for active distribution networks[J]. Sustainable Cities and Society, 2020, 65: 102593.