|
|
|
发布时间: 2024-10-28 |
智能电网技术 |
|
|
|
收稿日期: 2024-03-19
基金项目: 国家自然科学基金(51977127);上海市教育发展基金会和上海市教育委员会“曙光计划”(20SG52)
中图法分类号: TM734
文献标识码: A
文章编号: 2096-8299(2024)05-0449-10
|
摘要
针对固定补偿电价造成的楼宇电能系统调度困难的问题,建立了一种考虑用户用能差异性的补贴模型和多目标楼宇电能优化调度模型。首先,将补贴电价和温度设定值按照峰、平、谷时段划分为3个优化调度时段,并且建立了动态补贴电价模型。其次,建立了考虑用户热舒适度和经济性的综合满意度模型,以用户综合满意度最优、总运行成本最小、日负荷峰谷差最小、峰负荷最小建立多目标优化模型。最后,仿真验证了所提模型在保证用户综合满意度的同时,能有效降低运行成本和负荷峰谷差。
关键词
多目标优化调度; 电采暖负荷; 用户用能差异性; 用户满意度
Abstract
In order to solve the problem of difficulty in the scheduling of building electric energy system caused by fixed compensation electricity price, a subsidy model considering the difference of user energy consumption and a multi-objective building electric energy optimization scheduling model are established. Firstly, the subsidized electricity price and temperature setting value are divided into three optimal dispatching periods according to the peark, shoulder, and offpeak periods, and the dynamic subsidized electricity price model is established. Secondly, the comprehensive satisfaction model considering the user's thermal comfort and economy is established, and the multi-objective optimization model is established with the optimal comprehensive satisfaction of the user, the minimum total operating cost, the smallest daily load peak-to-valley difference, and the smallest peak load. Finally, simulations are used to verify that the proposed model can effectively reduce the operating cost and load peak-to-valley difference while ensuring the comprehensive satisfaction of users.
Key words
multi-objective optimization scheduling; electric heating load; user energy consumption difference; user satisfaction
随着全球范围内城市化进程加速,城市人口出现了快速增长态势,楼宇建设规模日益扩大。楼宇作为能源消耗的重要领域,对电力系统的负荷需求不断增加。通过智能化、自动化的能源管理系统,可以更加精细地监测和控制楼宇能源消耗,实现能源利用的最优调度。
电采暖作为清洁取暖的重要设备之一[1],也是一种可调节负荷,占北方尖峰负荷的比重日益增加,电采暖负荷在我国北方每年以20%的速度快速增长。对于电采暖优化调度,研究者众多[2]。文献[3]根据一阶等效热参数建立了空调模型,评估了考虑用户舒适度情况下的集群式空调的需求响应潜力。文献[4]考虑用户舒适度,建立了电采暖集群控制策略,依靠对电采暖的集群调度,提高了新能源的利用率。文献[5]则基于天气预报温度参数,深入探究了不同功率下电采暖的可调节能力,同时确保用户舒适度不受影响。在宏观层面,以电力公司调度成本最小化为目标,通过负荷聚合商对空调负荷进行优化调度;在微观层面,以空调利益最大化为导向,评估其调节潜力,并据此制定实际削减计划。文献[6]提出了一种聚合模型,充分考虑了温控负荷的异质性特点,在保障用户舒适度的前提下,进一步提出了一种创新的分组控制策略,旨在有效应对不同温控负荷之间的差异,并根据用户的实际需求进行科学的分组控制,从而实现对负荷的精细管理。
对于楼宇优化问题,在目前的研究中,运行成本最小化是最为常见的目标,同时用户舒适度、峰谷差以及分布式能源利用率也成为重要目标。文献[7]研究了基于用户满意度指数的户用微电网需求响应策略,用户满意度指数由用户用电舒适度、设备使用优先级和经济性组成,可以提高用户参与需求响应活动的积极性。文献[8]建立了个人舒适度模型,利用该模型对空调进行优化和控制,并对参与优化调度的用户给予一定的电价补贴,使用户参与优化调度。该模型根据电价、室外温度和用户偏好优化空调运行,在有效保证用户舒适度的同时,显著降低了用电成本。采用基于用户舒适度和能耗的多目标空调优化方法,获得了令人满意的决策结果。文献[9]给予用户固定的电价补贴,使电动汽车根据需求响应进行充放电。现有研究大多采用固定的补偿电价,虽然可以促进用户参与优化调度,但不能充分调动用户的积极性,所以本文将采用波动的补偿电价模型。文献[10]提出了一个基于空调能耗和热舒适性的多目标优化模型,并得出了均衡的决策结果。文献[11]提出了一种综合考虑用户舒适度和经济需求的电热水器灵活调度方案,建立了以电费和舒适度为目标的多目标优化模型,并采用遗传算法进行求解,确定了电热水器的启停时段。
针对固定补偿电价无法调动用户积极进行需求响应的问题,本文提出了一种考虑用户用能差异性的多目标楼宇电能优化调度模型。首先,提出一种随着用户参与调峰响应程度而变化的补贴电价模型,并把一天分为峰、平、谷3个优化调度时段;其次,考虑不同用户热舒适度和经济性的差异性,建立楼宇用户综合满意度模型;最后,以用户综合满意度最优、运行成本最小、日负荷峰谷差最小、峰负荷最小为目标,建立楼宇多目标调峰优化调度模型。算例结果证明所提调度模型的有效性。
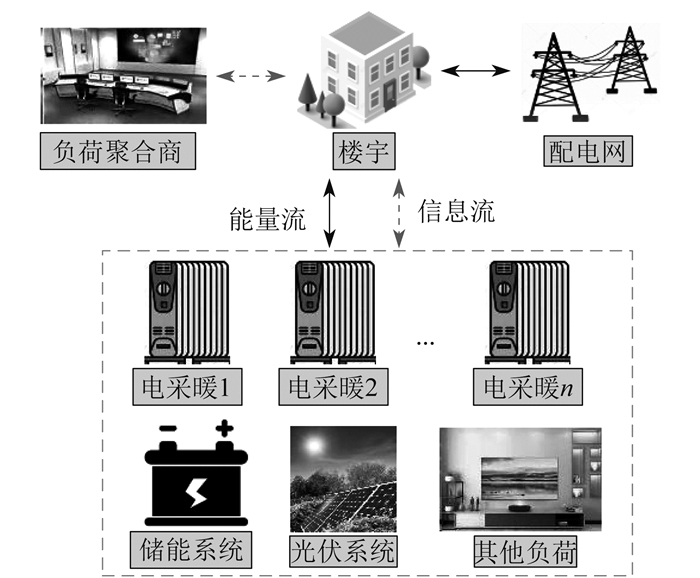
1 楼宇电能架构
本文建立的楼宇电能架构如图 1所示。其主要组成部分为光伏系统、储能系统、电采暖负荷以及基础的电负荷。
楼宇内部采集用户室内温度数据,并将这些数据传输给负荷聚合商。负荷聚合商综合考虑室外温度和楼宇总负荷波动性,制定相应的电采暖负荷和储能系统的启停策略。室内温度数据的采集可以帮助监控楼宇内部的能耗状况,以便进行合理的电能调度和管理。负荷聚合商作为能源管理的中介,通过分析室内温度、室外温度以及整体负荷情况,制定合适的用能策略,以确保楼宇能源的有效利用和管理,同时提供舒适的室内环境。
2 楼宇负荷模型
2.1 直热式电采暖模型
对于直热式电采暖的室内温度变化与电采暖功率之间的关系,采用一阶ETP模型热力学等效热参数模型表示[12]。
该模型可以描述室内空气的热力学特性和电能平衡。直热式电采暖模型为
| $ C \frac{\mathrm{~d} T_{\text {in }}}{\mathrm{d} t}=Q_{\text {heat }}(t)-\frac{Q_{\text {low }}(t)}{R} $ | (1) |
式中:C——等效热容;
Tin——房间内的温度;
Qheat (t)——t时刻房间内增加的热量;
Qlow (t)——t时刻房间内减少的热量;
R——等效热阻。
室内增加的热量来源于电采暖产出的热量Qhp (t),表达式为
| $ Q_{\text {heat }}(t)=Q_{\mathrm{hp}}(t)=\eta_{\text {eh }} P_{t}^{\text {eh }} $ | (2) |
| $ P_{t}^{\text {eh }}=S P_{t}^{\text {heat }} $ | (3) |
式中:ηeh——直热式电采暖设备的产热转化效率,设为0.85;
Pteh——t时刻电采暖的运行功率;
S——电采暖工作状态变量,S=0为电采暖停止工作,S=1为电采暖开始工作;
Ptheat——t时刻电采暖制热功率。
电采暖工作状态变量为
| $ S= \begin{cases}0, & T_{\text {in }}(t) \geqslant T_{\text {set }}(t)+\frac{\delta}{2} \\ 1, & T_{\text {in }}(t) \leqslant T_{\text {set }}(t)-\frac{\delta}{2}\end{cases} $ | (4) |
式中:δ——温度的死区宽度,取2 K;
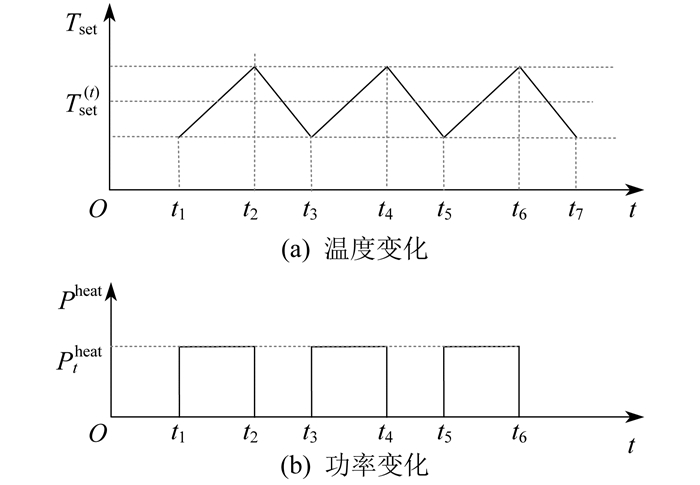
Tset (t)——t时刻设定温度,当室内温度大于设定最大值时停止运行,室内温度小于设定最小值时启动运行。
电采暖运行特性见图 2。横坐标为时间,纵坐标分别为设定温度Tset和电采暖制热功率Pheat。
t时刻房间内减少的热量Qlow (t)为
| $ Q_{\text {low }}(t)=\frac{T_{\text {in }}(t)-T_{\text {out }}(t)}{R} $ | (5) |
式中:Tout (t)——室外温度。
2.2 储能系统模型
在充放电过程中,储能系统在t时刻的荷电状态为
| $ S_{t}^{\mathrm{ESS}}=S_{t-1}^{\mathrm{ESS}}+\frac{\left(P_{t}^{\mathrm{c}} \eta_{\mathrm{c}}-P_{t}^{\mathrm{d}} \eta_{\mathrm{d}}\right)}{E_{\mathrm{ESS}}} \Delta t $ | (6) |
式中:StESS,St-1ESS——t、t-1时刻储能系统的荷电状态;
Ptc,Ptd——t时刻储能充电和放电功率;
ηc,ηd——储能充电和放电效率;
EESS——储能系统的额定容量;
Dt——时间间隔。
3 楼宇多目标优化模型构建
3.1 用户满意度模型
考虑到用户满意度,从用户热舒适度和经济性两个方面进行建模。为实现楼宇的电力调峰目标,将调峰时段划分为3个时段,这3个时段分别对应着电价的峰、平、谷。
3.1.1 舒适度
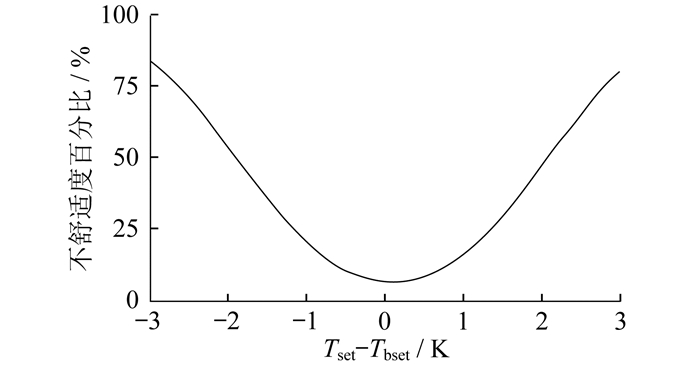
温度的设定与用户的舒适度有关,在一定的舒适度范围内,可以对温度进行调整。利用ASHRAE全球热舒适数据库Ⅱ可视化网站上的问卷调查[13]得到了用户不满意百分比概率曲线关系图,如图 3所示。其中,Tbest为用户最舒适温度。
对曲线进行拟合可以得到温度与不舒适度之间的关系式为
| $ f(T)=a\left(T_{\text {set }}-T_{\text {best }}\right)^{2}+b\left(T_{\text {set }}-T_{\text {best }}\right)+c $ | (7) |
式中:f(T)——温度T与不舒适度的关系函数;
a,b,c——用户舒适度模型系数。
为了方便理解,将式(7)简化为温度与舒适度的模型,即:
| $ \begin{align*} F(T)= & 1-\left\{a\left[T_{\text {set }, i}(t)-T_{\text {best }, i}\right]^{2}+\right. \\ & \left.b\left[T_{\text {set }, i}(t)-T_{\text {best }, i}\right]+c\right\} \end{align*} $ | (8) |
式中:F(T)——温度与舒适度的模型;
Tset,i(t)——t时刻用户i的设定温度;
Tbest,i——用户i的最舒适温度。
选择峰、平、谷3个时段,每个时段的温度设定一致。
3.1.2 经济性
本文提出了一种波动的补偿模型,通过差异化激励的方式实现补偿。根据用户设定的温度与最舒适温度之间的差异程度,补贴电价会有所不同。当用户设定温度与最舒适温度相差较大时,补贴电价会更高;当差距较小时,补贴电价则较低。通过将差异化激励和用户类型考虑在内,这种补偿模型可以更好地调整用户的舒适度体验,并为用户提供合理的激励,促使用户积极参与负荷削减。一元二次曲线的补偿模型如下:
| $ c_{\mathrm{BT}, t}= \begin{cases}\frac{c_{\mathrm{sub}, t}}{\left(T_{\max }-T_{\min }\right)^{2}}\left(T_{\mathrm{set}}-T_{\text {best }}\right)^{2}, & T_{\mathrm{set}}<T_{\text {best }} \\ 0, & T_{\mathrm{set}} \geqslant T_{\text {best }}\end{cases} $ | (9) |
式中:cBT,t——t时刻波动的补贴电价;
csub,t——t时刻基础补贴电价;
Tmax——保证用户热舒适度下温度设定上限,一般比最适宜温度高3 ℃;
Tmin——保证用户热舒适度下温度设定下限,一般比最适宜温度低3 ℃。
采用参与调峰前后的电采暖用户用电成本的比值衡量用户的经济性,可表示为
| $ F(C)=1-\frac{C-C_{0}}{C} $ | (10) |
式中:F(C)——用户经济性;
C——参与调峰后电采暖用电成本;
C0——参与调峰前电采暖用电成本。
F(C) < 1表示参与调峰后用电成本增加,用户的经济性低于未参与调峰时的经济性;F(C) > 1表示参与调峰后用电成本降低,用户的经济性比未参与调峰时好;F(C)= 1表示用户的经济性与未参与调峰时一样。F(C)越大,表示电采暖用户的经济性越好,用户的经济满意度越高。
参与调峰后的电采暖用电成本为
| $ C=\sum\limits_{t}\left(P_{t}^{\mathrm{eh}} c_{\mathrm{B}}\right)-\sum\limits_{t}\left(p_{\mathrm{BT}, t}\right) $ | (11) |
式中:cB——楼宇购电价格;
pBT,t——t时刻参与调峰给予的电费补贴。
参与调峰给予的电费补贴如下:
| $ p_{\mathrm{BT}, t}= \begin{cases}c_{\mathrm{BT}, t}\left(P_{t}^{\mathrm{eh} 0}-P_{t}^{\mathrm{eh}}\right), & P_{t}^{\mathrm{eh} 0} \geqslant P_{t}^{\mathrm{eh}} \\ 0, & P_{t}^{\mathrm{eh} 0}<P_{t}^{\mathrm{eh}}\end{cases} $ | (12) |
式中:Pteh0——t时刻未参与优化调度时的电采暖功率。
参与调峰前的电采暖用电成本为
| $ C_{0}=\sum\limits_{t}\left(P_{t}^{\mathrm{eh} 0} c_{\mathrm{B}}\right) $ | (13) |
3.1.3 用户综合满意度
为了全面分析用户的满意度,将用户舒适度与经济性相结合。若舒适度≤1,则用户用电经济性 > 1。定义综合满意度为
| $ \begin{equation*} U_{i}=\beta_{1} F\left(T_{i, \text { 谷 }}\right) \beta_{2} F\left(C_{i, \text { 谷 }}\right)+\beta_{1} F\left(T_{i, \text { 平 }}\right) \beta_{2} F\left(C_{i, \text { 平 }}\right)+\\ \;\;\;\;\;\;\;\beta_{1} F\left(T_{i, \text { 峰 }}\right) \beta_{2} F\left(C_{i, \text { 峰 }}\right) \end{equation*} $ | (14) |
式中:Ui——综合满意度;
β1,β2——舒适度和经济性的偏好因子,且β1 + β2 = 2;
Ti,谷,Ti,平,Ti,峰——用户i在3个时段的温度;
Ci,谷,Ci,平,Ci,峰——用户i在3个时段的电采暖用电成本。
β1越大,β2就越小,代表用户i对电采暖舒适度要求越高,可以适当降低经济性;β1越小,β2就越大,代表用户i对经济性要求高,希望节省用电成本,所以可以适当降低舒适度要求。用户的偏好因子受用电习惯、经济情况、年龄等因素的影响,不同用户的偏好因子值也会有所不同[14]。
电采暖的启停情况受温度设定的影响,因为用户具有用能差异性,故感受的最舒适温度不同,可以设定的温度范围也有所不同。每栋楼内房间众多且用户的温度设定存在差异,如果将每个房间的每小时温度设定都作为决策变量,那么求解过程将变得繁琐且耗时。因此,需要对楼宇中的电采暖用户进行简化处理。
一是按群体简化。根据经济、年龄和衣着情况,将用户分为9类:高收入衣着多青年群体、中等收入衣着多青年群体、低收入衣着多青年群体、高收入衣着少青年群体、中等收入衣着少青年群体、低收入衣着少青年群体、高收入老年群体、中等收入老年群体、低收入老年群体。
二是按时间段简化。在用户电采暖温度设定方面,应避免24 h内所有用户群体设为同一温度区间所带来的不合理性。在峰、平、谷3个时段,分别设置不同的温度设定值,并且在每个时段内温度设定值保持不变。
综上所述,根据用户用能的差异性和不同时段的需求,本文将一天分为峰、平、谷3个时段,并将楼宇中的电采暖用户划分为9个不同的用户群体。针对每个时段和每类用户群体设定相应的温度区间,共将27个温度设定值作为调峰优化问题的决策变量。这样有助于更好地满足用户的需求,合理分配能源消耗,提高能源利用效率。
3.2 目标函数
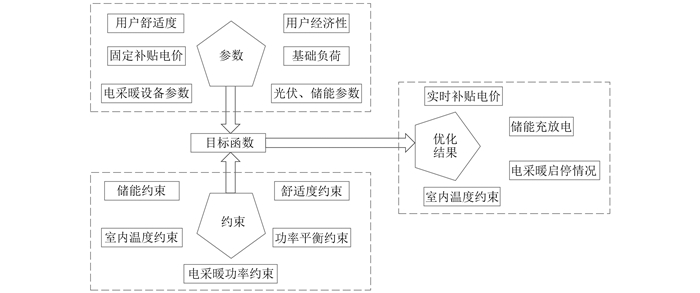
本文目的是在满足用户满意度的前提下,通过调峰优化来确保电力系统的安全稳定运行[15]。为了实现这一目标,需要对峰谷差进行调整,同时也需要考虑用户行为的差异性。因此,建立了一个楼宇优化调度模型,如图 4所示。
需要实现以下几个方面的优化目标,即最小化日负荷曲线的峰负荷、最小化日负荷曲线的峰谷差、最大化用户综合满意度以及最小化楼宇总运行成本。基于该模型,可以在保障用户满意度的情况下优化能源利用,并确保电力系统的稳定运行。
考虑用户用能差异性的楼宇系统的子目标函数共有4个。
目标函数1为最大化用户综合满意度函数U,表示为
| $ U=\max U_{i} $ | (15) |
目标函数2为楼宇总运行成本最小化函数,表示为
| $ \min E=\sum\limits_{t}\left(c_{\mathrm{B}} P_{t}^{\mathrm{B}}\right)+c_{\mathrm{PV}} \sum\limits_{t}\left(P_{t}^{\mathrm{PV}}\right)+c_{\mathrm{ESS}} \sum\limits_{t}\left(P_{t}^{\mathrm{c}}+P_{t}^{\mathrm{d}}\right)-\\ \;\;\;\;\;\;\;\sum\limits_{t}\left(c_{\mathrm{S}} P_{t}^{\mathrm{S}}\right)-\sum\limits_{t}\left(p_{\text {Вт }, t}\right) $ | (16) |
式中:E——楼宇运行总成本;
PtB,PtS——楼宇t时刻的购电量和售电量;
cPV——光伏运行所需的成本;
PtPV——t时刻的光伏发电量;
cESS——充放电成本;
cS——楼宇售电价格。
目标函数3为日负荷曲线峰负荷最小化函数P,表示为
| $ P=\min \left(\max\limits_{0 \leqslant 24} P_{t}\right) $ | (17) |
| $ P_{t}=P_{i, t}^{\mathrm{Base}}+\sum\limits_{i} P_{i, t}^{\mathrm{eh}}+P_{t}^{\mathrm{c}}-P_{t}^{\mathrm{d}} $ | (18) |
式中:Pt——t时刻楼宇负荷总功率;
Pi,tBase——t时刻其他负荷i功率;
Pi,teh——t时刻用户i的电采暖运行功率。
目标函数4为最小化日负荷曲线峰谷差ΔP,表示为
| $ \Delta P=\min \left(\max\limits_{0 \leqslant t \leqslant 24} P_{t}-\min\limits_{0 \leqslant t \leqslant 24} P_{t}\right) $ | (19) |
3.3 约束条件
电采暖功率约束条件为
| $ 0 \leqslant P_{i, t}^{\mathrm{eh}} \leqslant P_{i, t}^{\text {heat }} $ | (20) |
式中:Ptheat——t时刻电采暖制热功率。
室内温度约束条件为
| $ \left\{\begin{array}{c} T_{\text {set }}(t)-\frac{\delta}{2} \leqslant T_{\text {in }}(t) \leqslant T_{\text {set }}(t)+\frac{\delta}{2} \\ T_{\text {best }}(t)-3 \leqslant T_{\text {set }}(t) \leqslant T_{\text {best }}(t)+3 \end{array}\right. $ | (21) |
舒适度约束条件为
| $ 0 \leqslant F(T) \leqslant 1 $ | (22) |
用户舒适度保持在0到1之间,不得小于零。
补贴电价约束条件为
| $ 0 \leqslant c_{\mathrm{BT}, t} \leqslant c_{\mathrm{sub}, t} $ | (23) |
储能系统的充放电约束和荷电状态约束条件为
| $ \left\{\begin{array}{c} 0 \leqslant P_{t}^{\mathrm{c}} \leqslant P_{\max }^{\mathrm{c}}, 0 \leqslant P_{t}^{\mathrm{d}} \leqslant P_{\max }^{\mathrm{d}}\\ S_{\min }^{\mathrm{ESS}} \leqslant S_{t}^{\mathrm{ESS}} \leqslant S_{\max }^{\mathrm{ESS}} \end{array}\right. $ | (24) |
式中:Pmaxc——最大充电功率;
Pmaxd——最小放电功率;
SminESS——最小荷电状态;
SmaxESS——最大荷电状态。
储能系统不能同时充放电,即
| $ P_{t}^{\mathrm{c}} P_{t}^{\mathrm{d}}=0 $ | (25) |
式(15)与式(16)、式(17)、式(19)相互冲突,难以同时满足。本文采用设定权值法,将多个目标函数转化为单目标问题,转化后的目标函数W为
| $ \begin{align*} W= & \min \left(\lambda_{1} \frac{\max\limits_{0 \leqslant t \leqslant 24} P_{t}}{\max\limits_{0 \leqslant t \leqslant 24} P_{0}(t)}+\right. \\ & \left.\lambda_{2} \frac{\max\limits_{0 \leqslant t \leqslant24} P_{t}-\min\limits_{0 \leqslant t \leqslant 24} P_{t}}{\max\limits_{0 \leqslant t \leqslant 24}(t)-\min\limits_{0 \leqslant t \leqslant 24} P_{0}(t)}+\lambda_{3} \frac{E}{E_{0}}-\lambda_{4} U_{i}\right) \end{align*} $ | (26) |
| $ \lambda_{1}+\lambda_{2}+\lambda_{3}+\lambda_{4}=1 $ | (27) |
| $ E_{0}=\sum\limits_{t}\left(c_{\mathrm{B}} P_{t}^{\mathrm{B}}\right)+c_{\mathrm{PV}} \sum\limits_{t}\left(P_{t}^{\mathrm{PV}}\right)+c_{\mathrm{ESS}} \sum\limits_{t}\left(P_{t}^{\mathrm{c}}+P_{t}^{\mathrm{d}}\right)- \\ \;\;\;\;\;\;\;\sum\limits_{t}\left(c_{\mathrm{S}} P_{t}^{\mathrm{s}}\right) $ | (28) |
式中:λ1,λ2,λ3,λ4——4个子目标函数的权重值;
P0(t)——未参与优化调度时t时刻楼宇负荷总功率;
E0——未参与优化调度时总运行成本。
这样可以避免由最大负荷、峰谷差与楼宇总运行成本之间数量级差别太大所导致的误差问题。考虑到目标函数3、目标函数4体现的都是优化调度对削峰填谷的影响,同时目标函数2~4的变化趋势相同且有所关联,因此设定目标函数2~4的权值相同,则目标函数转化为
| $ \begin{align*} W= & \min \left\{\frac { \lambda _ { 1 } } { 3 } \left[\frac{\max\limits_{0 \leqslant t \leqslant 24} P_{1}(t)}{\max\limits_{0 \leqslant t \leqslant 24} P_{t}}+\right.\right. \\ & \left.\left.\frac{\max\limits_{0 \leqslant t \leqslant 24} P_{1}(t)-\min\limits_{0 \leqslant t \leqslant 24} P_{1}(t)}{\max\limits_{0 \leqslant t \leqslant 24} P_{t}-\min\limits_{0 \leqslant t \leqslant 24} P_{t}}+\frac{E}{E_{0}}\right]-\lambda_{2} U_{i}\right\} \end{align*} $ | (29) |
| $ \lambda_{1}+\lambda_{2}=1 $ | (30) |
式中:P1(t)——参与优化调度后t时刻楼宇负荷总功率。
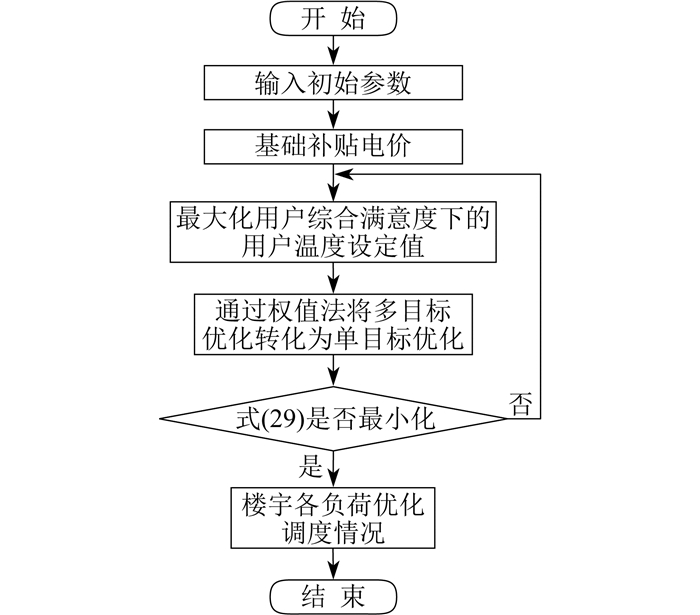
对于不同的优化目标[16],λ1和λ2的取值并不相同。当要求楼宇总运行成本更低和削峰填谷效果更好时,λ1的取值应更大一些。使用MATLAB R2023b软件通过YALMIP工具箱调用CPLEX 12.10.0求解器进行求解。通过权值法,将多目标优化问题转化为单目标优化问题,在求解式(29)目标函数的同时,满足式(20)至式(28)所示的约束条件。求解流程见图 5。
4 算例分析
4.1 基础数据
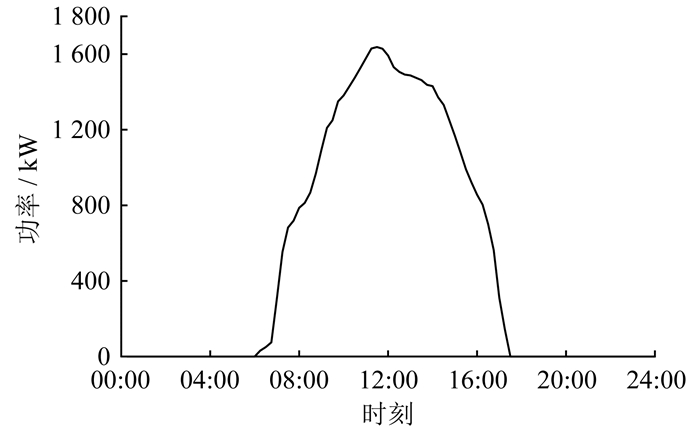
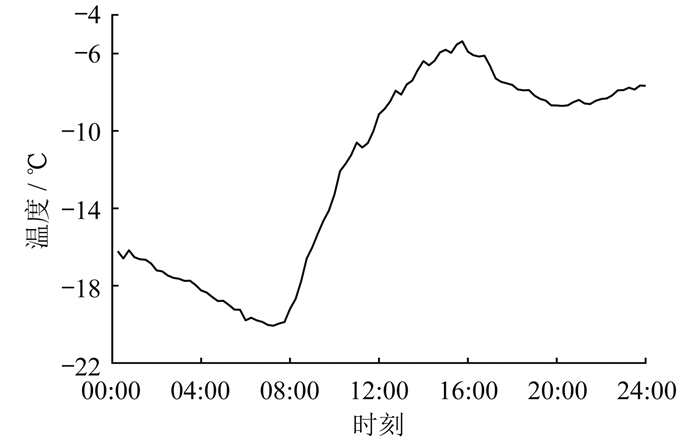
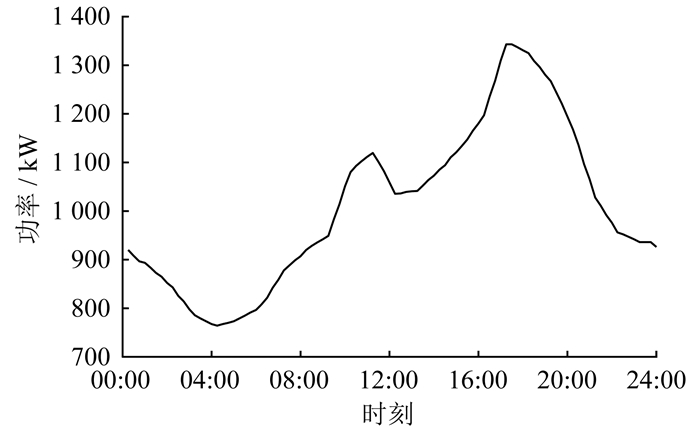
算例考虑用户用能差异性的楼宇负荷优化调度问题,以冬季某典型日的用电情况为例,15 min为时间间隔,全天24 h共有96个时间点进行优化调度。根据用户特性不同,将用户分为9类,每类用户的房间安装一台电采暖负荷,每类用户的数量在[5, 10]之间随机选取。楼宇配有光伏系统和储能系统,光伏装置额定容量为1 700 kW。楼宇光伏输出功率、典型日室外温度、其他负荷功率曲线分别如图 6、图 7、图 8所示。购售电价格和基础补贴电价如表 1所示[17]。
表 1
电价
| 时段类型 | 时段 | 购电价格 | 售电价格 | 基础补贴电价 |
| 谷 | 00:00—8:00 | 0.40 | 0.12 | 0.20 |
| 平 | 08:00—10:00 | 0.90 | 0.27 | 0.40 |
| 15:00—17:00 | ||||
| 22:00—24:00 | ||||
| 峰 | 10:00—15:00 | 1.30 | 0.39 | 0.50 |
| 17:00—22:00 |
对每户安装控制器,实时采集室温和电采暖负荷的启停状态,并通过发送控制指令来控制电采暖负荷,方便负荷聚合商对电采暖负荷直接进行优化调度,同时便于用户自主控制。电采暖、楼宇参数设置分别如表 2、表 3所示。
表 2
电采暖参数
| 参数 | 用户1 | 用户2 | 用户3 | 用户4 | 用户5 | 用户6 | 用户7 | 用户8 | 用户9 |
| 等效热容C/(kJ/℃) | 0.82 | 0.84 | 0.83 | 0.82 | 0.84 | 0.84 | 0.84 | 0.83 | 0.82 |
| 等效热阻R/(℃/kW) | 38.44 | 43.36 | 35.83 | 38.44 | 43.36 | 43.36 | 39.09 | 39.58 | 34.18 |
| 电采暖功率Piheat/kW | 6.90 | 6.80 | 7.00 | 6.90 | 6.80 | 7.00 | 6.90 | 6.80 | 7.00 |
表 3
楼宇参数
| 参数 | 数值 |
| 储能充电效率ηc | 0.95 |
| 储能放电效率ηd | 1.05 |
| 储能充电功率Pmaxc/kW | 150 |
| 储能放电功率Pmaxd/kW | 150 |
| 储能运行成本ESSc/(元/kWh) | 0.01 |
| 荷电状态上限SmaxESS | 0.9 |
| 荷电状态下限SminESS | 0.1 |
| 额定容量EESS/kWh | 1 000 |
| 光伏运行成本cPV/(元/kWh) | 0.008 5 |
根据ASHRAE全球热舒适数据库Ⅱ可视化网站上的问卷调查结果,对用户不满意度曲线进行拟合,得到衣着指数a、b、c和最舒适温度,如 表 4所示。根据用户对舒适度和经济性要求不同设定β1和β2。
表 4
用户满意度参数
| 用户 | 用户舒适度模型系数 | 最舒适温度/℃ | β1 | β2 | ||
| a | b | c | ||||
| 1 | 0.103 9 | 0.002 7 | 0.045 8 | 23 | 1 | 1 |
| 2 | 0.066 2 | -0.116 7 | 0.058 3 | 22 | 1 | 1 |
| 3 | 0.159 9 | -0.114 4 | 0.064 4 | 20 | 1 | 1 |
| 4 | 0.103 9 | 0.002 7 | 0.045 8 | 23 | 0.9 | 1.1 |
| 5 | 0.066 2 | -0.116 7 | 0.058 3 | 22 | 0.9 | 1.1 |
| 6 | 0.159 9 | -0.114 4 | 0.064 4 | 20 | 0.9 | 1.1 |
| 7 | 0.103 9 | 0.002 7 | 0.045 8 | 23 | 0.8 | 1.2 |
| 8 | 0.066 2 | -0.116 7 | 0.058 3 | 22 | 0.8 | 1.2 |
| 9 | 0.159 9 | -0.114 4 | 0.064 4 | 20 | 0.8 | 1.2 |
4.2 仿真结果分析
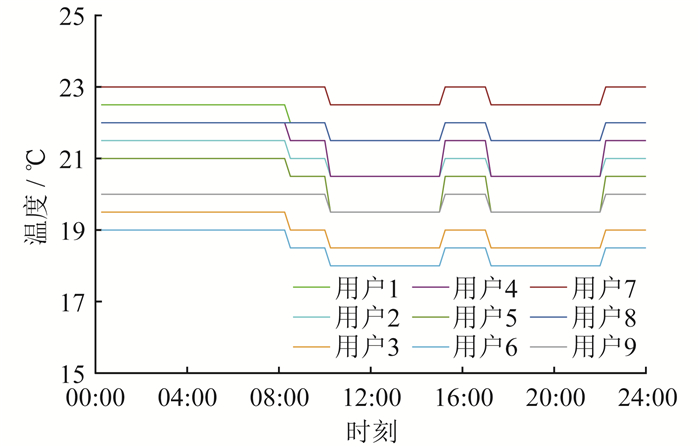
图 9为用户一天内电采暖负荷的温度设定值。
由图 9可知,对用户舒适度和经济性设计后,电采暖的温度设定更加合理。
通过纵向对比可以看出:用户7~9对舒适度要求高,对经济性要求低,所以在00:00—10:00、15:00—16:00、22:00—24:00时段,将温度设定为最舒适温度,并在10:00—14:00和17:00—21:00时段响应负荷聚合商的调峰需求,在用电高峰期将温度设定下降0.5 K,这样既响应了调峰需求,又不会损失太多热舒适度;用户1~6均在00:00—24:00时段将温度下调,用户4~6对经济性要求高,所以在10:00—14:00、17:00—21:00电价高峰时段大幅下调温度,以达到经济性更优的效果。横向对比可以看出:夜间,用户都在家中,室外温度较低,且电价和补贴电价都处于较低水平,所以温度设定较高;而白天,家中无人,室外温度高,且电价和补贴电价都较高,所以温度设定有所降低。因为对用户满意度进行设计时考虑了用户用能差异性,根据电价的峰、平、谷时段对用户的温度设定划分了时段,避免了全天24 h温度设定值一样带来的用电需求的不合理性。
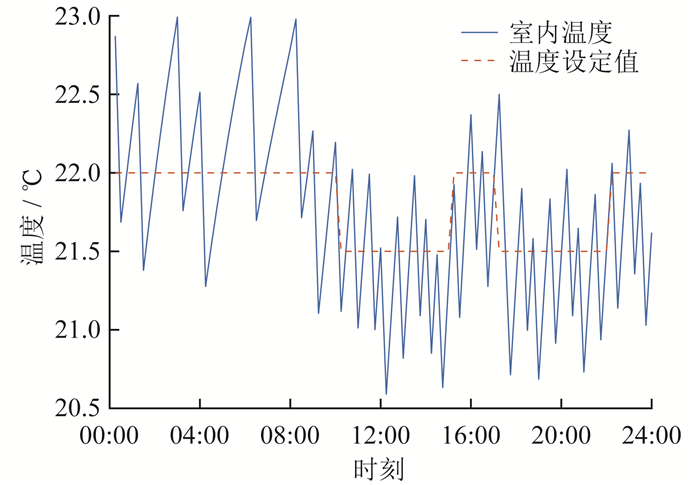
图 10是用户8参与优化后室内温度的变化情况。以用户8为例,根据温度波动情况可以分析出电采暖启停的情况。室内温度基本处于温度设定阈值的下限,可以降低成本,但也损失用户的热舒适度。在08:00—24:00时段,除了温度设定值变化的时刻,温度波动都很小,维持在温度设定阈值的下限。室外温度此时(08:00—24:00)较高,楼宇处于用电高峰期,电采暖因为室外温度的原因更快地到达设定温度,所以可以减低楼宇总负荷的峰值(此时不太可能每个用户的电采暖负荷都处于开启,因而电采暖运行功率很高的概率很小)。
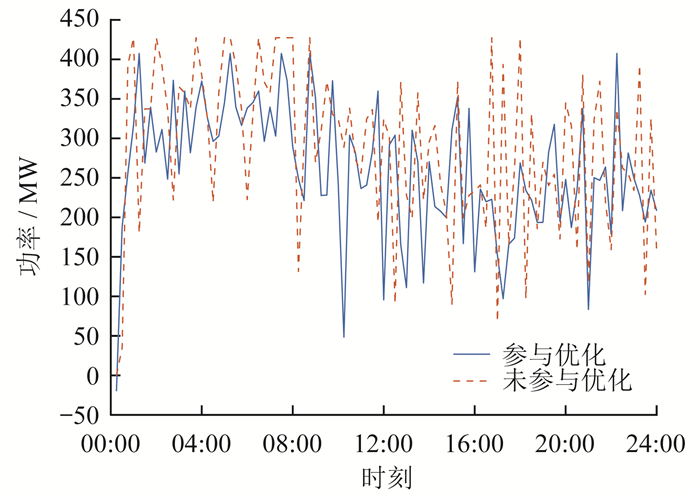
用户参与优化前后电采暖的功率变化曲线如 图 11所示。由图 11可以看出:用户参与优化后的功率均略小于未参与优化时的功率;在电价高峰期,用户温度设定值降低更多,对应功率下降得也更多一点。因为电采暖设备设置了温度范围,所以功率曲线会来回波动。
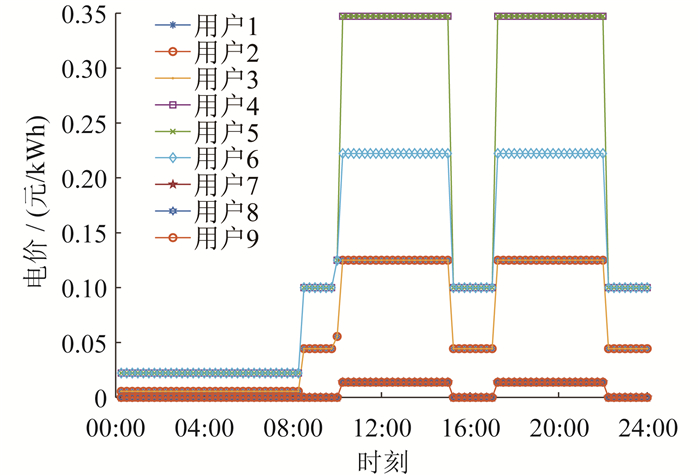
根据用户设定的温度变化而调整的补贴电价如图 12所示。用户7、用户8和用户9在10:00—14:00、17:00—21:00时段温度降幅最小,因此补贴电价相对较低,在00:00—09:00、15:00—16:00、22:00—24:00时段,将温度设定为最舒适温度,其对应补贴电价为0元/kWh。对于用户1~6,在峰、平、谷各时段,随着温度降低程度增大,补贴电价逐渐提高。在用户损失舒适度时,给予补贴电价进行经济补偿。补贴电价不是固定不变的,而是根据用户设定的电采暖负荷温度值而动态调整。设定值越低,舒适度损失越大,补贴电价就越高,经济性补贴越多,以此来达到用户满意度最优的效果。
表 5为在冬季典型日优化前后楼宇负荷的指标变化情况。
表 5
冬季典型日优化前后楼宇负荷的指标变化情况
| 权重 | 最大负荷/kW | 最小负荷/kW | 峰谷差/kW | 总运行成本/元 | 用户满意度 | |
| λ1 | λ2 | |||||
| 0 | 0 | 1 758.14 | 881.84 | 876.30 | 15 591.31 | 0 |
| 0.6 | 0.4 | 1 510.89 | 1 154.76 | 356.13 | 15 498.93 | 0.85 |
| 0.5 | 0.5 | 1 530.90 | 1 134.84 | 396.06 | 15 520.90 | 0.88 |
| 0.4 | 0.6 | 1 575.66 | 1 130.43 | 445.23 | 15 587.30 | 0.92 |
λ1 = 0,λ2 = 0对应的是未参与优化时的指标变化情况。根据表 5,以权重λ1 = 0.6、λ2 = 0.4为例,楼宇的最大负荷由1 758.14 kW下降到1 510.89 kW,最小负荷由881.84 kW上升到1 154.76 kW,楼宇的峰谷差由876.30 kW下降到356.13 kW,使得负荷峰谷差明显减少,负荷曲线明显改善,削峰填谷效果比较明显。总运行成本也由15 591.31元降低到15 498.93元。随着用户满意度目标函数权重λ1的逐渐增加,总运行成本也逐渐增加。权重λ1 = 0.5、λ1 = 0.4时的总运行成本与权重λ1 = 0.6时相比,分别增加了21.97元和88.37元;峰谷差和最大负荷也不断增加,权重λ1 = 0.5和权重λ1 = 0.4时的峰谷差与权重λ1 = 0.6时相比,分别增加了39.93 kW和89.10 kW。随着权重λ1增大,用户综合满意度占比也不断增加。这表明用户对满意度要求高时,对电网的响应就会变差,因此选择合适的目标函数权重,可以在保证用户满意度的前提下达到最好的削峰填谷效果。
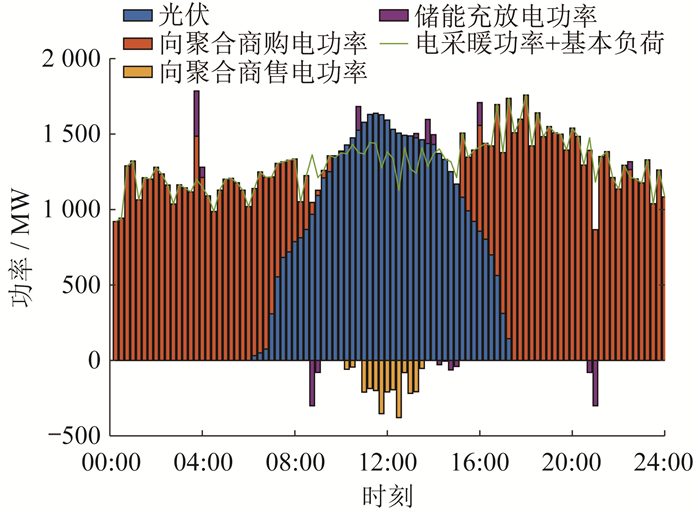
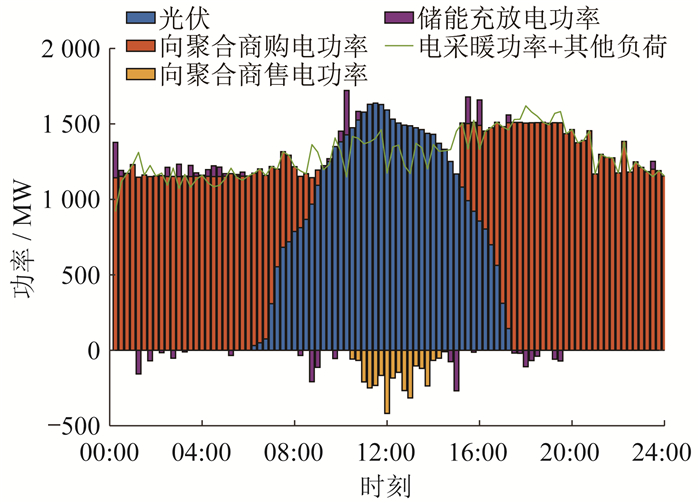
图 13和图 14分别是未参与优化调度时和参与优化调度后时的楼宇负荷情况。可以看出,实施动态补贴电价后,楼宇负荷高峰有所下降,负荷低谷有所上升,但楼宇负荷曲线与未参与调峰优化时的走势基本相同。
由图 13可以看出,储能系统在电价低谷时进行充电,在电价高峰且用电高峰时段进行放电操作。在10:45—14:00时段,因为光伏输出功率过剩,所以储能系统进行充电,并且将部分功率出售给负荷聚合商,以此来获得收益;在14:30—15:00时段,电价较高,进行放电操作,以达到降低运行成本的效果。
由图 14可以看出,与图 13相比,其向负荷聚合商购电功率的变化比较平缓。以00:00—15:00为例,其中00:15—05:45时段属于电价低谷时段,此时对储能系统进行充电。电价低时充电,电价高时放电,可以降低运行成本。有多个时段处在楼宇负荷低谷时期,储能进行充电操作可以增加楼宇负荷的功率,增大最小负荷值。在01:15—01:30、02:00—02:30、03:15—03:30时段,因为基础用电负荷加上电采暖功率,此时处于一个用电小高峰,储能进行放电操作,可以减小楼宇负荷值,使楼宇总负荷变得平稳。08:00—09:45时段电价稍高,处于电价平时段,储能进行放电操作可以降低运行成本。在10:45—13:30时段,因为光伏输出功率过剩,所以对储能系统进行充电,并且将部分光伏输出功率出售给负荷聚合商。因为如果把全部的光伏输出功率都储存到储能系统,就使得运行功率的最大负荷值过大。为了降低峰值,将部分光伏输出功率出售。13:45—15:00时段是电价峰时段,储能系统进行放电操作,可以降低运行成本,同时降低此段负荷的峰值。因此,本文提出的优化模型可以有效降低楼宇负荷最大值,提高楼宇负荷最小值,减小峰谷差,对调峰的需求响应有积极作用,并且可以减小楼宇运行成本。
5 结语
本文首先综合考虑用户经济水平、健康情况和年龄等用户电采暖负荷响应能力的影响因素,并根据这些影响因素将用户分为9类进行研究,对参与调峰的用户给予电价补贴,补贴电价的多少与用户响应程度有关。然后建立了考虑用户满意度、削峰填谷效果和总运行成本的多目标优化调度模型。结果表明,在考虑用户满意度的情况下,所建模型能够最大限度地降低楼宇负荷最大值,增大楼宇负荷的最小值,平缓负荷曲线,起到削峰填谷的效果,并且能有效减小楼宇总运行成本。需要说明的是,本文对楼宇中负荷建模不够全面,目前的楼宇负荷不止电采暖负荷、储能系统和光伏系统。下一步对楼宇优化调度的研究将会考虑更多负荷,如电动汽车、电热水器等,以完善负荷建模。
参考文献
-
[1]宋杰, 李树鹏, 张卫国, 等. 含蓄热式电采暖的综合能源系统日前优化调度策略研究[J]. 智慧电力, 2021, 49(4): 14-20.
-
[2]刘萌, 梁雯, 张岩, 等. 计及空调负荷群控制的源-荷协同优化调度模型[J]. 电网技术, 2017, 41(4): 1230-1238.
-
[3]杨梓俊, 丁小叶, 陆晓, 等. 面向需求响应的变频空调负荷建模与运行控制[J]. 电力系统保护与控制, 2021, 49(15): 132-140. DOI:10.19783/j.cnki.pspc.200548
-
[4]杨玉龙, 王甜甜, 陈祥, 等. 考虑新能源消纳的电采暖集群多功率级控制策略研究[J]. 电力系统保护与控制, 2022, 50(10): 20-30. DOI:10.19783/j.cnki.pspc.210872
-
[5]黄亚峰, 朱玉杰, 穆钢, 等. 基于温度预报的户用电采暖负荷可调节能力评估[J]. 电网技术, 2018, 42(8): 2487-2493.
-
[6]LIN S F, LIU D F, HU F, et al. Grouping control strategy for aggregated thermostatically controlled loads[J]. Electric Power Systems Research, 2019, 171: 97-104. DOI:10.1016/j.epsr.2019.02.005
-
[7]郭晓利, 赵莹, 曲楠, 等. 基于满意度的户用型微电网多属性需求响应策略[J]. 太阳能学报, 2021, 42(7): 22-27. DOI:10.19912/j.0254-0096.tynxb.2018-0042
-
[8]WU Y, CAO B, HU M, et al. Development of personal comfort model and its use in the control of air conditioner[J]. Energy and Building, 2023, 285: 112900. DOI:10.1016/j.enbuild.2023.112900
-
[9]于浩, 沈运帷, 林顺富, 等. 考虑用户心理的商业楼宇集群能量共享优化策略[J]. 电网技术, 2022, 46(11): 4423-4436.
-
[10]LIN C J, WANG K J, DAGNE T B, et al. Balancing thermal comfort and energy conservation: a multi-objective optimization model for controlling air-condition and mechanical ventilation systems[J]. Building and Environment, 2022, 219: 109237. DOI:10.1016/j.buildenv.2022.109237
-
[11]武媚, 包宇庆, 张金龙, 等. 计及用户舒适度的电热水器多目标优化控制策略[J]. 电力工程技术, 2019, 38(3): 100-107.
-
[12]CHEN W Q, LIN X F, LI Y F, et al. Planning method for regenerative electric heating system considering the heat load during power outage[C]//2021 11th International Conference on Power and Energy Systems (ICPES). Shanghai, China, 2021: 564-568.
-
[13]Centre for Built Environment Team. ASHRAE global thermal comfort database Ⅱ visualization[EB/OL]. (2014-08-09)[2024-02-19]https://cbe-berkeley.shinyapps.io/comfortdatabase/.
-
[14]杨悦, 宋良泰. 考虑用户需求响应的空调负荷日前-实时聚合调控[J]. 全球能源互联网, 2023, 6(5): 529-537.
-
[15]赵倩, 刘励行. 基于差分进化算法的多目标优化V2B2模式的调度策略[J]. 上海电力大学学报, 2022, 38(2): 105-111. DOI:10.3969/j.issn.2096-8299.2022.02.001
-
[16]赵鑫, 李晓露. 计及灵活性需求偏差的综合能源系统分布鲁棒优化调度[J]. 上海电力大学学报, 2023, 39(5): 426-435. DOI:10.3969/j.issn.2096-8299.2023.05.002
-
[17]范帅, 郏琨琪, 郭炳庆, 等. 分散式电采暖负荷协同优化运行策略[J]. 电力系统自动化, 2017, 41(19): 20-29. DOI:10.7500/AEPS20170227011