|
|
|
发布时间: 2024-10-28 |
智能电网技术 |
|
|
|
收稿日期: 2024-03-04
中图法分类号: TM715
文献标识码: A
文章编号: 2096-8299(2024)05-0459-09
|
摘要
深远海场景下的风电场受热带气旋等极端气候影响将产生大规模风电功率爬坡事件,严重威胁电网安全稳定运行。对此,提出了一种将深度强化学习和分布鲁棒优化结合起来平抑风电功率爬坡事件的储能容量优化配置方法。首先,基于改进旋转门算法识别风电功率爬坡事件,采用近端策略优化算法对风电功率爬坡事件进行平抑。其次,基于深度强化学习训练的模型,采用分布鲁棒优化对储能进行容量配置优化。最后,对不同场景下的储能容量配置结果进行比较分析。仿真结果验证了所提优化配置方法的有效性。
关键词
风电功率爬坡; 热带气旋; 储能配置; 近端策略优化算法; 分布鲁棒优化
Abstract
Wind farms in deep sea scenarios are affected by extreme climates such as tropical cyclones, which results in large-scale wind power ramp events, seriously affecting the safe and stable operation of the electrical power network. An optimal configuration method of energy storage capacity combining deep reinforcement learning with distributionally robust optimization to smooth wind power ramp events is proposed. Firstly, based on the improved swinging door algorithm, wind power ramp events is identified, and the proximal policy optimal algorithm is used to smooth wind power ramp events. Secondly, the model trained based on deep reinforcement learning uses distributionally robust optimization to optimize the capacity allocation of energy storage. Finally, the configuration results of energy storage capacity in different scenarios are compared and analyzed. The simulation results verify the effectiveness of the proposed optimization configuration method.
Key words
wind power ramping; tropical cyclones; configuration of energy storage; proximal policy optimal algorithm; distributionally robust optimization
随着能源枯竭和气候问题日益严峻,以风力发电为代表的新能源发电迅速发展。海上风能具有风速高、风切变指数小、风速稳定等特点。我国近海和深远海风能资源丰富,具有较大的开发前景,但由于近海风能资源利用趋于饱和,所以海上风电逐渐向深远海发展。
相较于陆上风电和近海风电,深远海风电更容易受到热带气旋等海洋气候的影响。热带气旋产生的具有高风速、较大风速变化等特点的极端场景会使风力发电的风电功率产生巨大波动,严重影响电网的安全稳定运行[1-2]。不同风电场景下的风电功率爬坡事件具有不同的特点,对不同场景下的风电功率爬坡事件进行研究,有助于及时采取有效措施,减小其影响。
储能装置响应速度快,具有较高的能量密度,能够有效平抑风电功率爬坡事件。但目前储能装置成本相对较高,难以在保证经济性的情况下完全满足风电功率平抑需求,因此需要合理配置储能容量[3-4]。在陆上、海上和受到热带气旋影响的深远海场景下,风电功率爬坡具有不同的规律。这会影响储能装置的类型选择以及储能容量、功率容量的配置,因而需要对不同场景下的风电功率爬坡进行比较分析。
目前,主要采用发电机调节、负荷响应、储能平抑、风电机组有序退出等方式平抑风电爬坡事件。文献[5]采用火电机组组合的方式对1 h内的风电功率爬坡事件进行平抑,以应对较高的风电功率爬坡率;文献[6]考虑电网弹性,基于发电机调节、负荷响应和有序弃风应对极端天气下的风电爬坡事件;文献[7]采用深度Q网络算法对风电爬坡过程中的自动发电控制参数进行拟合,并对其进行评估;文献[8]提出了日前能量最优平抑策略,通过引入价值函数构建日前爬坡事件平抑模型,并采用该模型求解了基于Q因子的事件优化问题;文献[9]构建了基于场景覆盖指数评估的日内平衡策略,通过调度减少弃风和切负荷事件;文献[10]采用合作博弈方式对风电场群爬坡进行协调控制,提高了风电场效益。此外,目前对于风电功率爬坡事件识别与检测的研究,大都从爬坡事件的定义出发,采用旋转门算法、权重系数法、机器学习等方法对风电功率爬坡事件进行识别和检测[11-12],而且对于风电功率爬坡事件平抑研究的场景主要集中在陆上和近海场景,对于深远海场景下复杂海洋气候的考虑较少。
储能容量配置优化主要对平抑数据进行处理,优化方法和鲁棒模型等都可以满足储能容量配置的经济性和鲁棒性要求。文献[13]提出了基于改进移动平均和集成经验模态分解的风电功率波动平抑方法,构建了储能经济性模型,并对不同储能容量配置进行了比较分析;文献[14]针对光伏电站的储能配置提出了双层决策框架,并采用不同的指标评估了储能配置结果;文献[15]采用改进灰色预测模型对储能长期容量配置进行了研究;文献[16]构建了多种混合储能系统数学模型,基于自适应变分模态分解对混合储能进行了容量优化配置;文献[17]在考虑复杂海洋气候条件影响的前提下构建了鲁棒机会约束模型,并对储能平抑风电功率预测误差进行了容量配置;文献[18]提出了基于贝叶斯理论的分布鲁棒优化,并对储能容量配置及其在不确定因素下的敏感性进行了分析。当前储能容量配置的研究主要针对风电、光伏等新能源并网和负荷波动进行平抑,并且主要从经济性和鲁棒性考虑,而对风电不同场景下爬坡事件平抑的研究较少。
本文主要考虑以热带气旋为代表的深远海复杂海洋气候对风电并网的影响,针对陆上风电、海上风电和考虑热带气旋影响的不同场景进行风电并网的储能容量配置研究,构建平抑风电功率爬坡事件的近端策略优化(Proximal Policy Optimization,PPO)算法模型,采用基于多离散场景的分布鲁棒优化对储能容量进行配置,并对不同场景下的储能容量配置结果进行比较分析。
1 风电功率爬坡的储能平抑优化模型
1.1 风电功率爬坡事件的识别与平抑
风电场由于风速的随机波动会产生风电功率爬坡事件。在深远海场景的热带气旋等极端天气下,短时间内较大的风速变化会使风电功率产生较大波动,而热带气旋的高风速可能会超过风机的切出风速,导致风电功率大幅下降,出现大规模风电功率爬坡事件。
风电功率爬坡事件的定义目前主要有3种:一是在规定时间内首末时间功率差的绝对值大于阈值;二是在规定时间内最大最小功率差的绝对值大于阈值;三是在规定时间内风电功率爬坡率的绝对值大于阈值。
对风电功率爬坡事件的识别可以有效辨识风电功率爬坡事件,进而对其进行平抑。旋转门算法是一种数据压缩算法,通过对相似趋势段的数据进行压缩提取风电功率区段来辨识风电功率爬坡事件[19]。图 1是一种基于自适应门控参数的旋转门算法示意图。其在旋转门算法的基础上对门控参数ΔE1、ΔE2进行自适应调整,可避免固定参数下的不同区段数据压缩效果出现较大差异。
自适应门控参数的旋转门算法基本流程如下:
(1) 设置初始门控参数和门控调整参数;
(2) 从初始点开始往后逐渐计算上下门的斜率,并记录上下门的最大和最小斜率;
(3) 当上下门打开的内角和大于等于180°时,循环结束并记录压缩区段;
(4) 若压缩区段与原数据之间的误差超出一定的阈值范围,则对门控参数进行修正并重新循环。上下门的斜率计算公式如下:
| $ \left\{ {\begin{array}{*{20}{l}} {{k_{n1}} = \frac{{{P_n} - {P_0} + \Delta {E_i}}}{{{t_n} - {t_0}}}}\\ {{k_{n2}} = \frac{{{P_n} - {P_0} - \Delta {E_i}}}{{{t_n} - {t_0}}}} \end{array}} \right. $ | (1) |
最大最小斜率计算公式如下:
| $ \left\{\begin{array}{l} k_{\max }=\max \left(k_{\max 0}, k_{n 1}\right) \\ k_{\min }=\min \left(k_{\min 0}, k_{n 2}\right) \end{array}\right. $ | (2) |
式中:kn1——上旋转门的斜率;
Pn——n点的功率;
P0——初始点的功率;
ΔEi——修正的门控参数,i为修正次数;
tn——n点的时间;
t0——初始点的时间;
kn2——下旋转门的斜率;
kmax——记录上旋转门的最大斜率;
kmax0——原最大斜率;
kmin——记录下旋转门的最小斜率;
kmin0——原最小斜率。
对门控参数的修正计算如下:若压缩区段与原数据之间的误差小于一定的阈值,则采用式(3) 对门控参数进行修正;若误差大于一定的阈值,则采用式(4)对门控参数进行修正。
| $ \left\{\begin{array}{l} \Delta E_{i}=\Delta E_{i-1}+\delta \\ i=i+1 \end{array}\right. \ $ | (3) |
| $ \left\{\begin{array}{l} \Delta E_{i}=\Delta E_{i-1}-\delta \\ i=i+1 \end{array}\right. $ | (4) |
式中:δ——修正量。
1.2 深度强化学习
深度强化学习在强化学习的基础上引入深度神经网络处理连续问题,在决策优化中有较为广泛的应用。其中行动器-判别器(Actor-Critic,AC)算法结合了基于策略的方法和基于价值的方法,其基本架构被广泛应用于深度强化学习算法中。AC算法通过构建策略网络和价值网络学习动作策略,其中:策略网络基于价值网络对动作的价值评估和环境反馈采取策略执行动作,策略网络通过与环境进行交互来改变状态参数并由环境反馈奖励;价值网络基于奖励和环境反馈对动作策略进行评估,基于收集的数据学习动作策略,帮助策略网络更新参数进而调整策略网络的动作,以此获得更多的奖励。
1.3 PPO算法
PPO算法是一种在线策略算法。其通过在AC算法框架的基础上采用PPO惩罚或PPO截断来限制策略更新。由于强化学习在训练后期需要足够小的学习率以确保策略收敛,因而强化学习在训练后期可能会出现较大波动,训练过程不稳定。而PPO算法通过将KL散度(Kullback-Leibler divergence)的约束加入目标函数中来限制策略更新,或者直接将目标函数进行限制。因此,PPO算法的训练过程相比于其他深度强化学习算法更加稳定,并且效果较好,具有较强的鲁棒性。
本文采用的是基于PPO截断方式的PPO算法。PPO截断的重要性权重用来衡量新旧策略的差异,通常表示为新旧策略的概率比。PPO截断根据重要性权重对目标函数进行限制。重要性权重的表达式为
| $\begin{equation*} r_{t}(\theta)=\frac{\pi_{\theta}\left(a_{t} \mid s_{t}\right)}{\pi_{\theta_{\text {old }}}\left(a_{t} \mid s_{t}\right)} \end{equation*} $ | (5) |
式中:rt(θ)——重要性权重;
t——时间;
θ——策略参数;
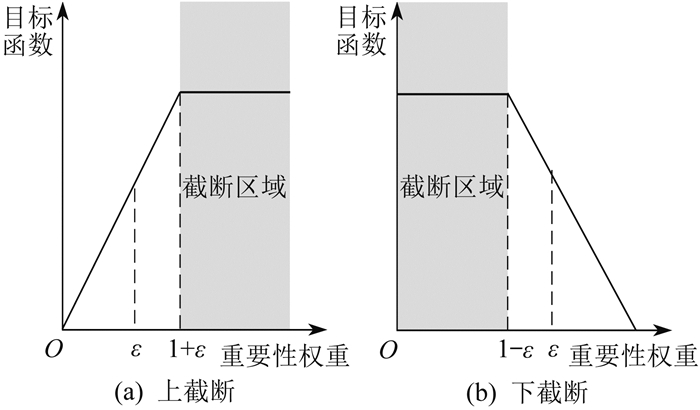
基于PPO截断的PPO算法直接基于截断阈值对优势函数进行裁剪,PPO截断示意如图 2所示。
ε为截断阈值,将重要性权重限制在[1−ε,1+ ε]范围内,通过对目标函数进行裁剪来限制新旧策略差异。
基于PPO截断的PPO算法的目标函数表达式为
| $ \begin{equation*} \mathcal{L}^{\text {CLIP }}(\theta)=\\ \hat{E}_{t}\left\{\min \left[r_{t}(\theta) \hat{A}_{t}, \operatorname{clip}\left(r_{t}(\theta), 1-\varepsilon, 1+\varepsilon\right) \hat{A}_{t}\right]\right\} \end{equation*} $ | (6) |
策略参数更新表达式为
| $ \begin{equation*} \theta_{k+1}=\arg \max\limits_{\theta} \mathcal{L}_{\theta_{k}}^{\mathrm{CLIP}}(\theta) \end{equation*} $ | (7) |
式中:
clip(a,b,c)——被定义为max[min(a,c),b];
深度强化学习通过环境设计来表现模型训练过程中相关参数的变化。状态空间为状态参数变化范围,动作空间为动作的变化范围。平抑风电功率爬坡事件深度强化学习的状态设置为时间,动作设置为储能充放电功率。智能体每次执行动作与环境进行交互为储能充放电行为,而环境在动作后的变化为经过一个时间间隔进入下一阶段;智能体不断地与环境交互,直至到达最终的时间点。
深度强化学习设置奖励函数与平抑所需的储能容量、风电爬坡功率平抑效果相关。奖励函数将主线奖励和辅助奖励结合:采用密集的辅助奖励为深度强化学习的训练提供依据,加快模型训练速度,同时将辅助奖励的值设置得相对较小,以避免陷入局部最优;基于每一轮完成目标达到终点的结果反馈主线奖励,由主线奖励确定模型最终的训练效果。由于优化目标是在满足平抑效果的情况下尽可能降低储能配置需求,降低储能配置成本,因而在奖励函数中还加入惩罚项以提高经济性。奖励函数的计算公式如下:
| $\begin{equation*} r_{m}=\sum\limits_{j=1}^{m}\left(k_{a} r_{\mathrm{a}}^{j}+k_{b} r_{\mathrm{b}}^{j}\right)+k_{f} r_{\mathrm{f}} \end{equation*} $ | (8) |
式中:rm——奖励函数;
m——每轮与环境交互的次数;
ka——每次与环境交互的奖励系数;
kb——每次与环境交互的惩罚系数;
2 储能容量配置模型
2.1 基于多离散场景的分布鲁棒优化
由于风电功率的随机性,储能容量配置优化问题难以用常规方法求解。针对含有随机变量的优化问题,通常采用鲁棒优化方法对随机变量构建模糊集来描述随机变量。分布鲁棒优化通过概率分布构建模糊集,可以避免一些极端情况,解决了传统鲁棒优化过于保守的问题。基于多离散场景的分布鲁棒优化通过有限的场景构建模糊集。一范数和无穷范数允许偏差限值如下:
| $ \left\{\begin{array}{l} \theta_{1}=\frac{N_{s}}{2 K} \ln \frac{2 N_{s}}{1-\alpha_{1}} \\ \theta_{\infty}=\frac{1}{2 K} \ln \frac{2 N_{s}}{1-\alpha_{\infty}} \end{array}\right. $ | (9) |
分布鲁棒不确定集合如下:
| $ \psi=\left\{P_{s} \in \mathbf{R}_{+}^{N_{s}} \left\lvert \begin{array}{l} \sum\limits_{s=1}^{N_{s}} P_{s}=1 \\ \sum\limits_{s=1}^{N_{s}}\left|P_{s}-P_{s}^{0}\right| \leqslant \theta_{1} \\ \max\limits_{1 \leqslant s \leqslant N_{s}}\left|P_{s}-P_{s}^{0}\right| \leqslant \theta_{\infty} \end{array}\right.\right. $ | (10) |
式中:θ1——一范数允许偏差限值;
Ns——典型场景数量;
K——样本总数;
α1——一范数置信度;
θ∞——无穷范数允许偏差限值;
α∞——无穷范数置信度;
ψ——不确定集合;
Ps——第s个典型场景的概率;
2.2 储能容量配置模型
配置储能平抑风电功率爬坡事件,并在满足爬坡平抑需求的情况下降低储能配置成本。储能容量配置模型的目标函数如下:
| $ \begin{equation*} \max \left(\sum\limits_{\substack{s=1 \\ P_{s} \in \psi \mu}}^{N_{s}} P_{s} F_{s}\right) \end{equation*} $ | (11) |
第s个典型场景的目标函数如下:
| $ \begin{equation*} F_{s}=\min \left(\boldsymbol{a}^{\mathrm{T}} x_{s}\right) \end{equation*} $ | (12) |
式中:Fs——第s个典型场景的目标函数;
aT——系数矩阵;
xs——第s个场景的决策变量。
储能装置容量配置约束条件,即储能可配置的容量及功率的范围满足约束条件,表示为
| $ \left\{\begin{array}{l} E_{\mathrm{C} \min } \leqslant E_{\mathrm{C}} \leqslant E_{\mathrm{C} \max } \\ P_{\mathrm{C} \min } \leqslant P_{\mathrm{C}} \leqslant P_{\mathrm{C} \max } \end{array}\right. $ | (13) |
式中:EC min——储能可配置的最小容量;
EC——储能配置容量;
EC max——储能可配置的最大容量;
PC min——储能可配置的最小功率容量;
PC——储能配置功率容量;
PC max——储能可配置的最大功率容量。
储能荷电状态约束条件,即储能荷电状态满足变化范围约束条件,表示为
| $ \begin{equation*} S_{\mathrm{OC}, \min } \leqslant S_{\mathrm{OC}} \leqslant S_{\mathrm{OC}, \max } \end{equation*} $ | (14) |
式中:SOC,min——储能最小荷电状态;
SOC——储能荷电状态;
SOC,max——储能最大荷电状态。
储能充放电功率约束条件,即储能充放电功率满足变化范围约束条件,表示为
| $ \begin{equation*} P_{\mathrm{C} \min } \leqslant P_{\mathrm{C}} \leqslant P_{\mathrm{C} \max } \end{equation*} $ | (15) |
式中:PC min——储能最小功率;
PC——储能功率;
PC max——储能最大功率。
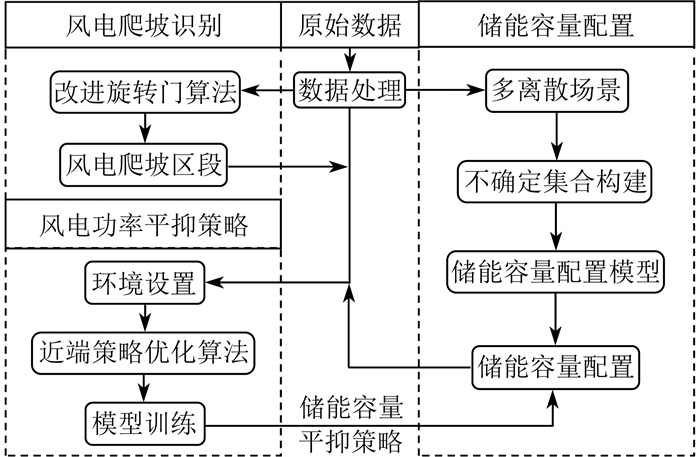
将分布鲁棒优化和近端策略优化方法结合,基于风电爬坡区段对风电功率进行平抑满足了风电爬坡平抑的鲁棒性和储能配置的经济性。图 3为平抑风电波动的储能配置框架图。采用改进旋转门算法进行风电爬坡识别,基于此设置深度强化学习环境,并采用近端策略优化算法对风电功率波动平抑策略进行模型训练,根据训练后的模型结合分布鲁棒优化对储能容量进行配置。
3 算例分析
3.1 算例参数
本文采用陆上风电场和海上风电场风电功率数据及热带气旋风速数据进行算例仿真分析,数据采样间隔时间为15 min。其中:陆上风电场装机容量为44 MW,有11台4 MW风机;海上风电场装机容量为111 MW,有18台6.2 MW风机。储能装置单位容量成本为120万元/MWh,单位功率成本为70万元/MW,储能装置充放电效率为95%[20]。本文仿真实验采用的软件如下:Python3.10.11,CUDA11.6,MATLAB R2016b,Python深度学习框架Pytorch1.13.1和Tensorflow 2.10.0,Python强化学习框架Stable Baselines3,MATLAB工具箱Yalmip,MATLAB求解器CPLEX12.8.0。
3.2 风电功率爬坡识别与储能平抑范围
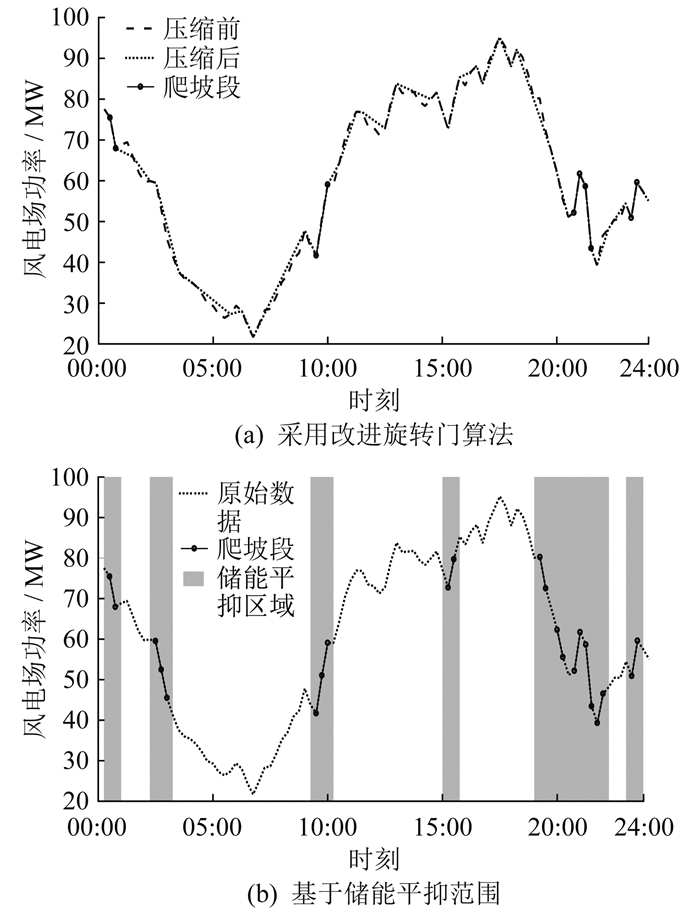
本文采用改进旋转门算法对风电功率爬坡事件进行识别。图 4为风电功率爬坡事件识别。其中图 4(a)、(b)分别为采用改进旋转门算法和基于储能平抑范围的风电功率爬坡事件识别。
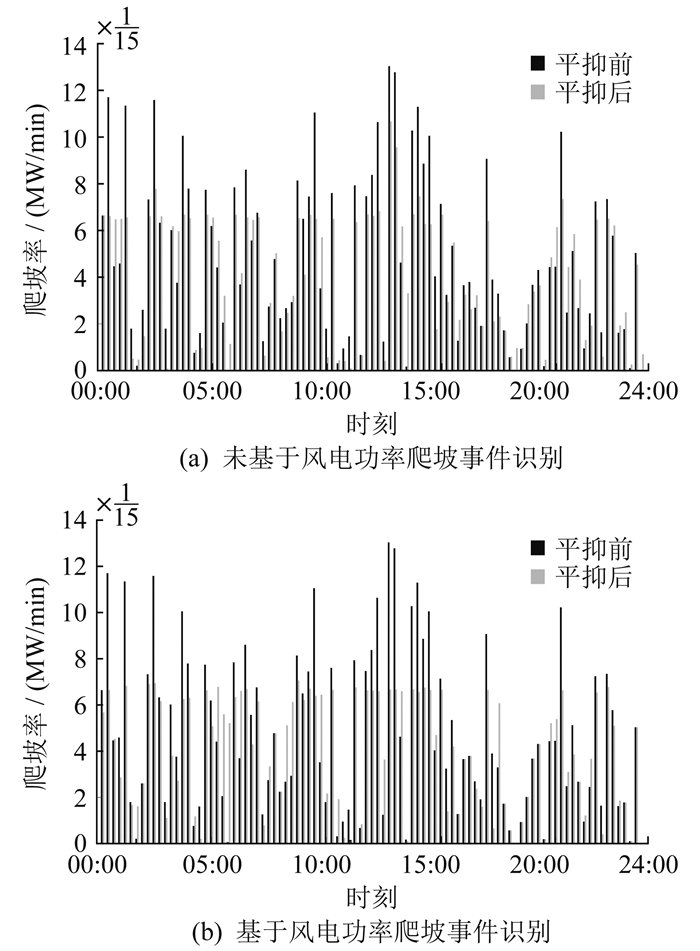
基于风电功率爬坡的储能平抑范围,采用深度强化学习对风电功率爬坡事件进行平抑。是否基于风电功率爬坡事件识别的平抑效果对比如图 5所示。其中,平抑前的动态波动指标为5.93,未基于风电功率爬坡事件识别进行平抑的动态波动指标为4.93,基于风电功率爬坡事件识别进行平抑的动态波动指标为4.81。由图 5及参数比较分析可知,在对风电功率爬坡事件识别后,基于风电功率爬坡的储能平抑范围,对风电功率爬坡事件进行平抑,在相同的训练次数下具有更好的效果。
3.3 不同深度强化学习算法比较
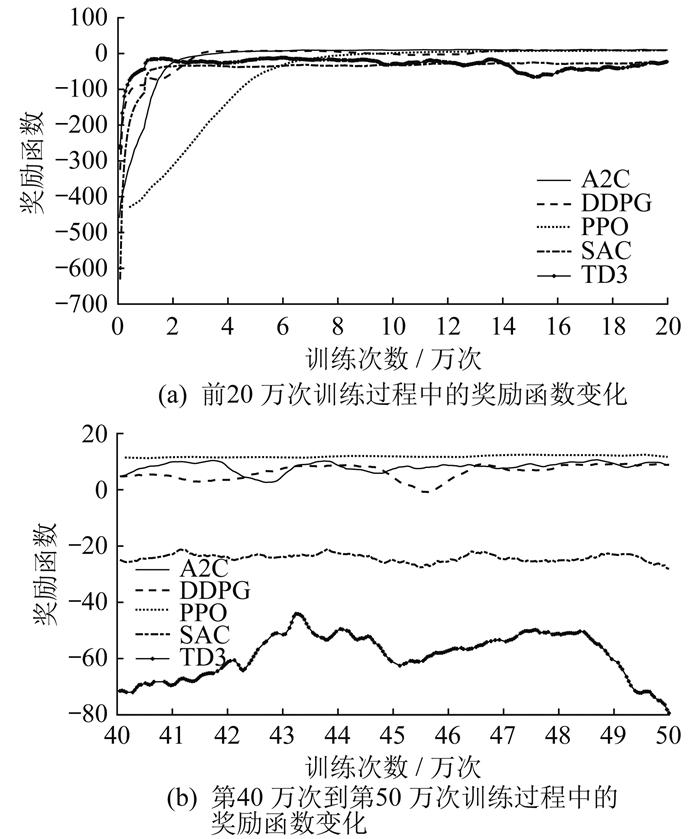
引入深度强化学习算法对风电功率爬坡事件进行平抑,对深度强化学习的优势行动器-判别器(Advantage Actor-Critic,A2C)、深度确定性策略梯度(Deep Deterministic Policy Gradient,DDPG)、PPO、柔性行动器-判别器(Soft ActorCritic,SAC)、双延迟深度确定性策略梯度(Twin Delayed Deep Deterministic policy gradient,TD3) 这5种算法的风电功率爬坡事件平抑效果进行比较分析。图 6为5种算法的奖励函数在训练过程中的变化。其中:图 6(a)为前20万次训练过程中的奖励函数变化,可以看出PPO算法在训练初期的收敛速度相比于其他算法更慢;图 6(b)为第40万次到第50万次训练过程中的奖励函数变化,可以看出在训练趋于收敛时,PPO算法的收敛过程最为稳定,且相比于其他算法效果更好。
3.4 不同场景下储能平抑风电功率爬坡
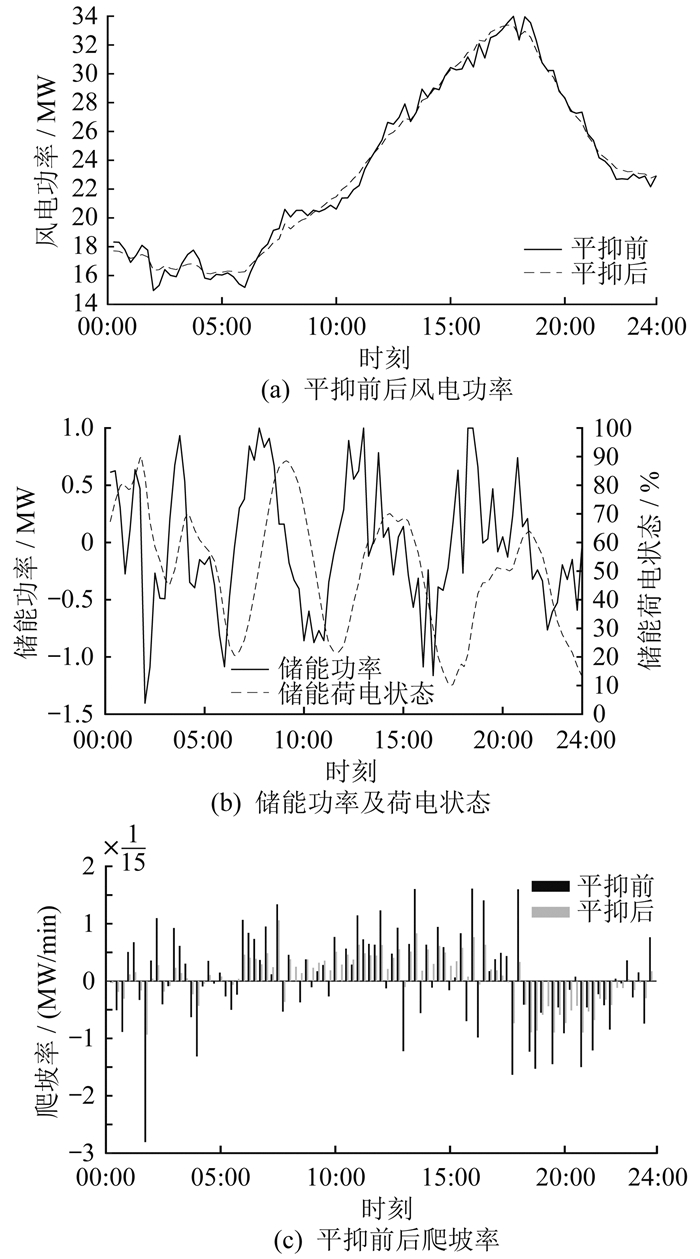
本文对陆上风电、海上风电和考虑热带气旋影响这3种场景下的风电功率爬坡事件进行平抑,图 7至图 9分别为3种场景下的储能平抑结果。由图 7至图 9可知,相比于陆上风电,海上风电场景下出现了更为频繁的风电功率爬坡事件,且爬坡率更高,而考虑热带气旋影响时可能会出现风速超出风机切出速度的情况,导致风机大规模切出,出现较大的风电功率爬坡事件。储能装置的平抑作用能够有效减小风电功率爬坡事件的爬坡率,避免风电功率爬坡事件对电网的冲击。
陆上风电场景下的储能平抑结果如图 7所示,其中图 7(a)、(b)、(c)分别为陆上风电场景下的平抑前后风电功率、储能功率及荷电状态、平抑前后爬坡率。由图 7可知,陆上风电功率爬坡事件较少且爬坡率较低,其所配置的储能容量和功率也较小,通过配置储能可以有效平抑陆上风电功率,减少爬坡事件。
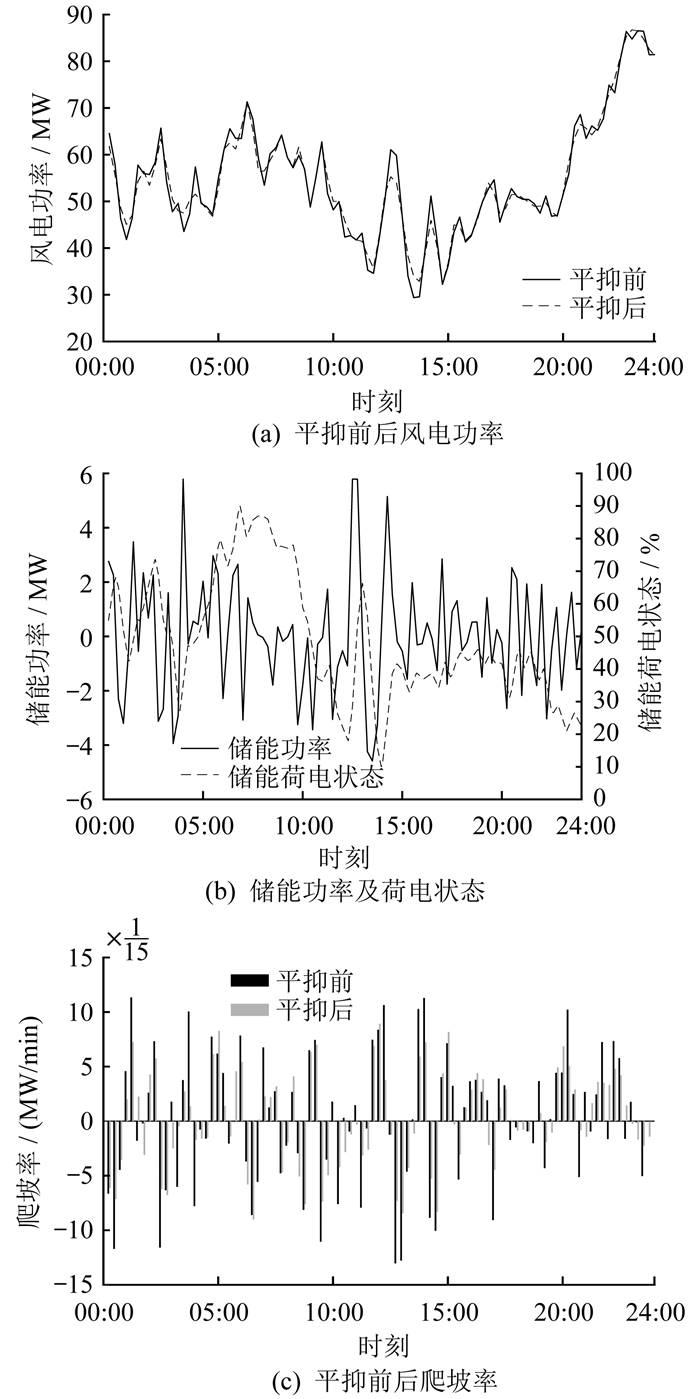
海上风电场景下的储能平抑结果如图 8所示,其中图 8(a)、(b)、(c)分别为海上风电场景下的平抑前后风电功率、储能功率及荷电状态、平抑前后爬坡率。由图 8可知,海上风电功率爬坡事件相比于陆上风电更多,且爬坡率更高,需要配置更多储能以平抑海上风电功率。同时,在海上风电场景典型日下,储能装置充放电相比于陆上风电更加频繁。
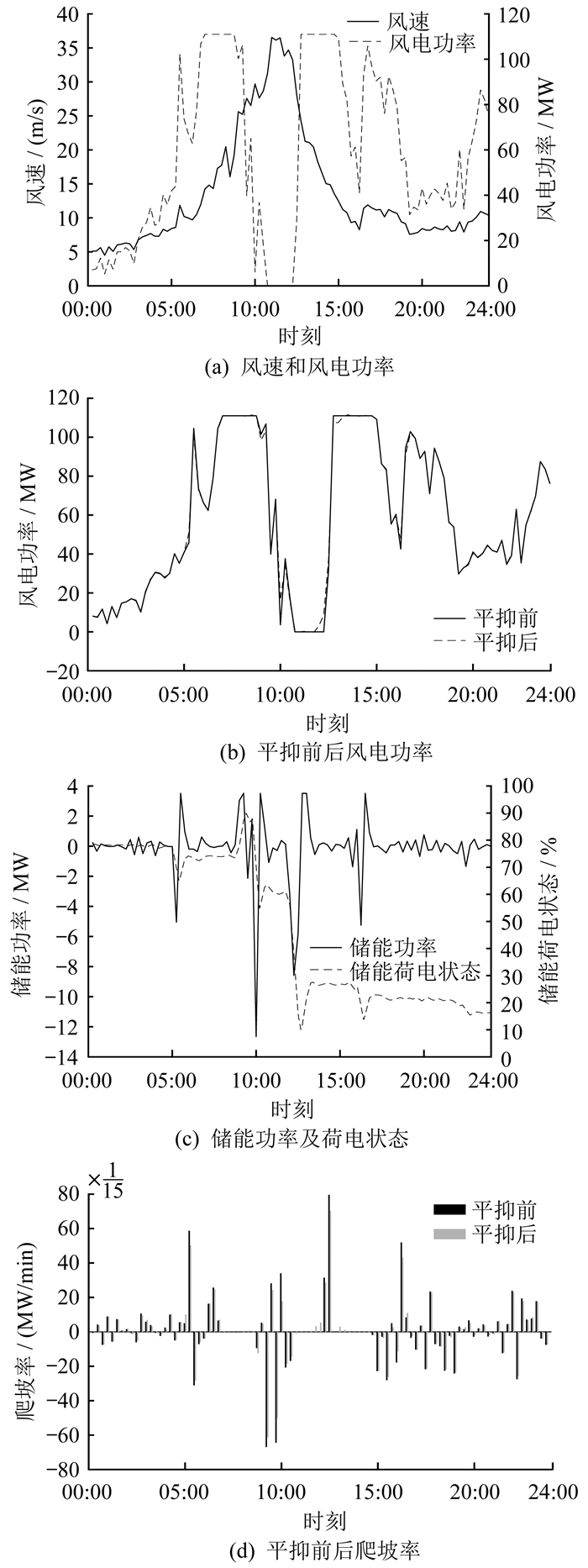
考虑热带气旋影响的海上风电场景下的储能平抑结果如图 9所示。其中图 9(a)、(b)、(c)、(d)分别为热带气旋场景下的风速和风电功率、平抑前后风电功率、储能功率及荷电状态、平抑前后爬坡率。由图 9可知,在热带气旋影响下,风速会出现较大的波动,甚至会超出风机切出风速而使风机切除,产生大规模风电功率爬坡事件,相比于海上风电需要配置更多储能,而且对配置储能的功率容量有更大的需求。
3.5 储能容量配置结果
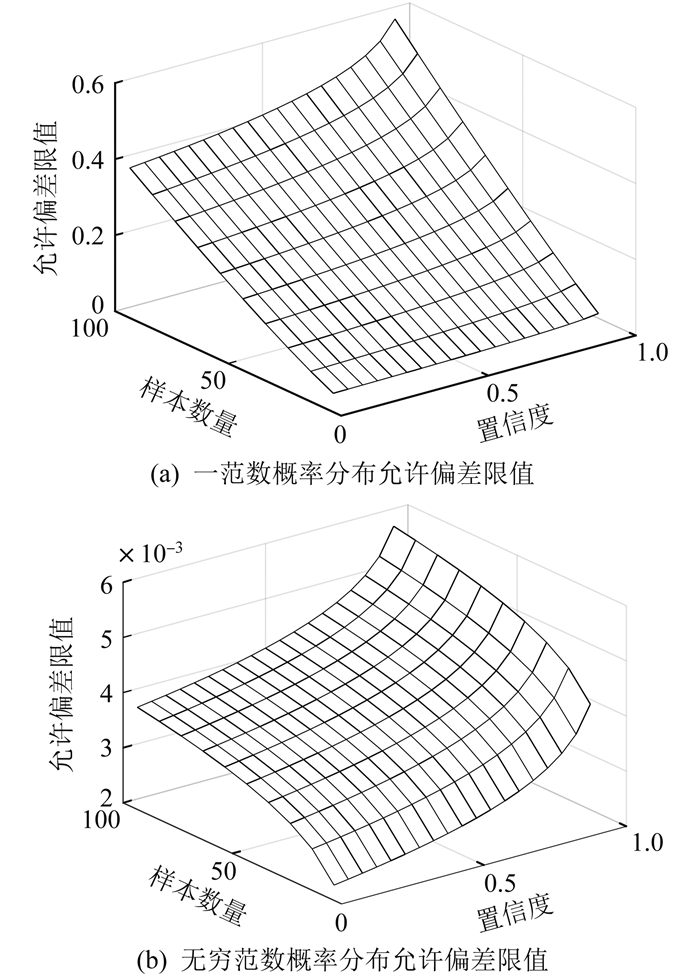
本文采用基于多离散场景的分布鲁棒优化方法对储能装置进行配置。不同置信度和样本数量下,一范数和无穷范数的概率分布允许偏差限值如图 10所示。由图 10可知,随着样本数量和置信度的增加,由样本数据确定的不确定变量概率分布更接近真实分布,配置的储能容量变小,避免了传统鲁棒优化过于保守的问题。
基于深度强化学习的训练模型和分布鲁棒优化的储能容量配置结果如表 1、表 2所示。由表 1可知:随着一范数置信度和无穷范数置信度的增加,不确定集描述的随机变量概率分布更趋于真实概率分布,所配置的储能容量减小;当一范数置信度与无穷范数置信度相比更大时,配置的储能容量基本不变,此时的不确定集主要受无穷范数置信度的影响。
表 1
不同参数下的储能容量配置结果
| α1 | 储能容量/MWh | ||
| α∞=0.5 | α∞=0.8 | α∞=0.95 | |
| 0.5 | 5.46 | 5.45 | 5.44 |
| 0.8 | 5.46 | 5.45 | 5.43 |
| 0.95 | 5.46 | 5.45 | 5.42 |
表 2
不同场景下的储能容量和储能功率配置结果
| 不同场景 | 储能容量/MWh | 储能功率/MW | 储能成本/万元 |
| 陆上风电 | 2.06 | 1.44 | 348.00 |
| 海上风电 | 5.42 | 6.03 | 1 072.50 |
| 考虑热带气旋 | 8.40 | 11.45 | 1 809.50 |
对陆上风电、海上风电和考虑热带气旋这3种不同场景下的储能容量和储能功率进行配置。由表 2及实测数据的风电场规模参数可知:陆上风电、海上风电和考虑热带气旋这3种场景下的储能容量配置比例分别为4.68%、4.88%、7.57%,储能功率依次增大。这一结果说明陆上风电、海上风电和考虑热带气旋这3种场景对储能装置充放电功率的需求依次增加。
4 结语
本文提出了一种深度强化学习和分布鲁棒优化结合的储能容量配置优化方法。基于风电功率爬坡识别的储能容量配置优化方法能够有效平抑风电功率爬坡事件,增强了储能平抑风电爬坡的鲁棒性,并有效降低了储能配置成本。不同场景下的储能配置结果显示,考虑热带气旋和海上风电这两种场景,相比于陆上风电场景,需要配置更多储能,并且对储能功率容量有更大的需求。在未来的研究中,可以引入深度学习方法,同时也可以考虑将发电机组和储能等多种方式结合起来对风电功率进行平抑,以应对不同场景下的风电功率爬坡事件。
参考文献
-
[1]PAUL S, NATH A P, RATHER Z H. A multi-objective planning framework for coordinated generation from offshore wind farm and battery energy storage system[J]. IEEE Transactions on Sustainable Energy, 2020, 11(4): 2087-2097. DOI:10.1109/TSTE.2019.2950310
-
[2]王骞, 张学广, 徐殿国. 考虑内-外生双重不确定性的风储系统联合规划方法[J]. 中国电机工程学报, 2023, 43(1): 169-181.
-
[3]HEMMATI R, MEHRJERDI H, SHAFIE-KHAH M, et al. Managing multitype capacity resources for frequency regulation in unit commitment integrated with large wind ramping[J]. IEEE Transactions on Sustainable Energy, 2021, 12(1): 705-714. DOI:10.1109/TSTE.2020.3017231
-
[4]付爱慧, 张峰, 张利, 等. 考虑爬坡功率有限平抑的高渗透率光伏电网储能配置策略[J]. 电力系统自动化, 2018, 42(15): 53-61.
-
[5]NYCANDER E, MORALES-ESPAÑA G, SÖDER L. Capacity and intra-hour ramp reserves for wind integration[J]. IEEE Transactions on Sustainable Energy, 2022, 13(3): 1430-1443. DOI:10.1109/TSTE.2022.3160842
-
[6]WANG Q, YU Z, YE R, et al. An ordered curtailment strategy for offshore wind power under extreme weather conditions considering the resilience of the grid[J]. IEEE Access, 2019, 7: 54824-54833. DOI:10.1109/ACCESS.2019.2911702
-
[7]ZHANG D, ZHANG H T, ZHANG X, et al. Research on AGC performance during wind power ramping based on deep reinforcement learning[J]. IEEE Access, 2020, 8: 107409-107418. DOI:10.1109/ACCESS.2020.3000784
-
[8]李江, 马昊天, 宋田宇. 风储联合系统爬坡事件的日前能量最优平抑方法[J]. 中国电机工程学报, 2021, 41(12): 4153-4164.
-
[9]亢丽君, 王蓓蓓, 薛必克, 等. 计及爬坡场景覆盖的高比例新能源电网平衡策略研究[J]. 电工技术学报, 2022, 37(13): 3275-3288.
-
[10]张旭, 代悦, 张东英, 等. 基于合作博弈的风电爬坡控制策略[J]. 电力系统自动化, 2019, 43(15): 42-48.
-
[11]YU S, HUR J. An enhanced performance evaluation metrics for wind power ramp event forecasting[J]. IEEE Access, 2023, 11: 100195-100206. DOI:10.1109/ACCESS.2023.3313632
-
[12]余洋, 陈东阳, 王卜潇, 等. 基于IBSO-SDT的风电爬坡事件检测方法[J]. 太阳能学报, 2023, 44(9): 348-355.
-
[13]YUMING C, PENG J, GAOJUN M, et al. Optimal capacity configuration of hybrid energy storage system considering smoothing wind power fluctuations and economy[J]. IEEE Access, 2022, 10: 101229-101236. DOI:10.1109/ACCESS.2022.3205021
-
[14]YAO M, CAI X. Energy storage sizing optimization for large-scale PV power plant[J]. IEEE Access, 2021, 9: 75599-75607. DOI:10.1109/ACCESS.2021.3081011
-
[15]LI J, FENG S, ZHANG T, et al. Study of long-term energy storage system capacity configuration based on improved grey forecasting model[J]. IEEE Access, 2023, 11: 34977-34989. DOI:10.1109/ACCESS.2023.3265083
-
[16]刘仲民, 齐国愿, 高敬更, 等. 基于自适应VMD的混合储能容量优化配置研究[J]. 太阳能学报, 2022, 43(4): 75-81.
-
[17]时帅, 吴慧娴, 黄冬梅, 等. 考虑复杂海洋气候条件影响的海上风电场储能容量配置研究[J]. 电力系统保护与控制, 2022, 50(10): 172-179.
-
[18]李笑竹, 王维庆. 基于贝叶斯理论的分布鲁棒优化在储能配置上的应用[J]. 电网技术, 2022, 46(10): 4001-4011.
-
[19]熊予涵, 彭小圣, 杨子民, 等. 基于参数自适应旋转门和Bump事件筛选的风电爬坡事件识别[J]. 南方电网技术, 2023, 17(2): 101-110.
-
[20]郝婷, 樊小朝, 王维庆, 等. 阶梯式碳交易下考虑源荷不确定性的储能优化配置[J]. 电力系统保护与控制, 2023, 51(1): 101-112.