|
|
|
发布时间: 2024-10-28 |
智能设备 |
|
|
|
收稿日期: 2024-03-26
基金项目: 国家自然科学基金(51907116);上海市自然科学基金(22ZR1425400)
中图法分类号: TM307
文献标识码: A
文章编号: 2096-8299(2024)05-0468-07
|
摘要
定子绕组匝绝缘劣化是导致变频电机故障的主要原因之一。通过在线监测其状态,可以及时发现潜在的安全隐患,但会面临匝绝缘劣化特性微弱的挑战。为了提高匝绝缘劣化灵敏度,提出了一种利用分数阶傅里叶变换结合卷积神经网络(FrFT-CNN)的变频电机匝绝缘状态监测方法。首先,在分数域内分析了高频开关振荡电流对匝绝缘变化的灵敏性。然后,设计了一种适用于变频电机匝绝缘状态监测的一维卷积神经网络模型。实验结果表明,与传统卷积神经网络方法相比,FrFT-CNN方法显著提高了匝绝缘状态监测的准确率,且兼具稳定性较高的优点。
关键词
匝绝缘; 变频电机; 分数阶傅里叶变换; 卷积神经网络; 状态监测
Abstract
The degradation of stator winding turn insulation is one of the primary causes of inverter-fed machine failures. Online monitoring of the stator winding turn insulation degradation can detect potential safety hazards in time, but faces the challenge of weak turn insulation degradation characteristics. In order to improve the sensitivity of turn insulation degradation, a turn insulation condition monitoring method for inverter-fed machine using fractional-order Fourier transform combined with convolutional neural network(FrFT-CNN)is proposed. Firstly, the sensitivity of the high-frequency switching oscillating current to the turn insulation change is analyzed in the fractional domain. Then, the one-dimensional convolutional neural network model suitable for turn insulation state monitoring of inverter motors is designed. The experimental results show that the FrFT-CNN method significantly improves the accuracy of turn insulation state monitoring compared with the traditional convolutional neural networks method, and also exhibits the advantage of higher stability.
Key words
turn insulation; inverter-fed machine; fractional fourier transform; convolutional neural networks; condition monitoring
可再生能源的大力发展推动了全球能源转型,风电、水电作为可再生能源的中坚力量,其电机驱动系统的重要性日益凸显[1]。变频电机因具有调速性能好、易启动、节能等优点,已广泛应用于新能源领域,现已成为当代电机驱动系统的主流[2]。
常见电机机器故障可分为轴承故障、定子相关故障和转子相关故障3类。根据调查研究,30%~40% 的电机故障与定子有关[3]。定子绕组绝缘作为驱动系统中最脆弱的部件之一,定子中大约80% 的电气故障源于薄弱的匝绝缘[4],尤其是近年来以碳化硅、氮化镓为代表的第3代宽禁带半导体正逐渐替代传统硅基电力电子器件,将会带来更快的开关频率和更高的工作电压,对电机绝缘系统带来更大挑战。
状态监测(Condition Monitoring,CM)被认为是可以提高功率器件可靠性的关键技术[5]。在线绝缘CM技术因其能够在不中断系统正常运行的情况下,提供有关绝缘健康状态的实时信息而越来越受到关注。现有的大多数CM方法主要针对主绝缘和相间绝缘,而对匝绝缘退化的研究非常有限。浪涌试验和局部放电试验是评估定子匝绝缘好坏的最常用技术[6]。但浪涌试验需要施加明显高于额定电压的脉冲,可能会对机器绝缘造成破坏。此外,在线局部放电试验易受逆变器电磁噪声的影响,因此不适用于低压电器。
绝缘电容可以作为反映定子绕组绝缘状态的可靠指标[7],但绝缘电容在低频段的阻抗非常大,可以达到MΩ级,测量其泄漏电流变化需要额外昂贵的传感器设备,因此近年来对绝缘状态的研究逐渐拓展到高频段,研究出高频信号注入法和逆变开关自激励法[8-9]。高频信号注入法需要一个额外的激励源,可能会影响系统的正常运行,而逆变开关自激励法利用逆变器本身的开关作为高频激励源,不会降低效率和可靠性。文献[9]通过测量逆变器开关所产生的电流响应来识别其高频特性,并通过实验证明了可以利用高频信息变化监测匝绝缘状态劣化。文献[10]尝试将开关瞬态时的电机振荡电流作为暂态响应,研究出通过开关瞬态频率响应曲线来监测早期匝绝缘状态的方法。文献[11]将共模平行谐振频率周围的开关振荡电流用于早期匝绝缘监测,定义并证明了开关振荡电流的尾分量可以作为监测匝绝缘劣化状态特征指标。
在匝绝缘劣化早期,由于开关振荡电流变化十分微小,因此在时域和频域的分辨率都较低。由海森堡的不确定性原理可知,信号在时域和频域分析中都不可能达到最佳分辨率[12]。分数阶傅里叶变换(Fractional Fourier Transform,FrFT)则提供了在时域和频域中间区域找到性能更好分数域的机会,通过分数阶变化,寻找更高的分辨率[13]。FrFT现已普遍应用于信号识别和雷达通信等领域[14]。卷积神经网络(Convolutional Neural Network,CNN)因其具有自适应提取特征和执行分类任务的特点而受到人们的关注[15],在图像处理、视频分析和电机故障辨识等领域均有出色表现。
针对开关振荡电流变化过于微小的问题,本文尝试利用FrFT来提高匝绝缘劣化状态监测的灵敏度。再设计轻量级一维CNN模型对电机匝绝缘状态进行监测,并通过实验验证该方法的有效性。
1 电机匝绝缘劣化原理
1.1 电机匝绝缘劣化
电机绝缘故障是一个缓慢发展的过程,一般由长期的匝绝缘劣化开始,匝绝缘失效后会导致匝间短路故障。匝间短路时,短路线圈内会产生很大的环流和大量热量,进而危害主绝缘和相间绝缘[16]。从单匝初期故障开始发展到严重绝缘故障的过程一般只需几秒(最快仅为2 s)到几小时。这就使得匝绝缘劣化成为电机绝缘监测中最需要关注的环节之一。
定子绝缘在老化过程中要承受电老化、热老化、机械老化等。绝缘电容在不同机理下发生不同变化。例如对聚酯酰亚胺电磁线进行热加速老化试验,其电容随绝缘降解而增大。因此,电容Ci的变化是由绝缘材料和降解机理决定的,可以作为早期绝缘老化的可靠指标。Ci的公式为
| $ \begin{equation*} C_{\mathrm{i}}=\varepsilon_{0} \varepsilon_{1} \frac{l_{\mathrm{i}} l}{2 e_{\mathrm{i}}} \end{equation*} $ | (1) |
式中:ɛ0,ɛ1——真空、绝缘材料的介电常数;
li,l——单匝导线的宽度和长度;
ei——匝绝缘厚度。
在实际应用场景下,电机匝绝缘电容一般在几百pF到几nF之间,电容相对的微小变化很难检测。
1.2 变频电机中高频开关振荡
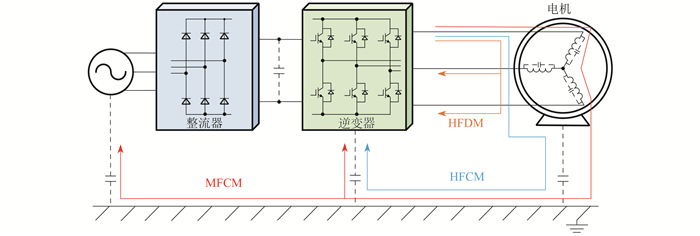
在变频电机系统中,电机的转动由脉冲宽度调制(Pulse Width Modulation,PWM)逆变器来控制。PWM逆变器作为很好的高频激励源,在开关过程中使得脉冲电压有着非常陡峭的上升/下降沿。PWM开关电流的振荡模式路径如图 1所示。在此激励下开关电流通过不同的高频寄生、分布参数,由高频耦合效应为开关电流提供不同的耦合路径,从而产生3种主要的振荡模态,分别为高频差模(High-Frequency Differential-Mode,HFDM)、高频共模(High-Frequency CommonMode,HFCM)和中频共模(Medium-Frequency Common-Mode,MFCM)。
由于绕组内寄生电容器的电容高于其终端寄生电容器,因此只有频率相对较低的MFCM电流通过电机绕组内匝绝缘的寄生电容,可以反应匝绝缘的状态。从振荡波形看,当HFDM和HFCM快速衰减后,可以看到表现为尾分量的MFCM。理论上,MFCM电流是由PWM电压励磁UPWM和尾分量频率下机器绕组Zcm的共模阻抗之间的相互作用决定的[11]。
| $ Z_{\mathrm{cm}}=\frac{L\left(C_{\mathrm{p}}+C_{\mathrm{g} 2}\right) s^{2}+\frac{L}{R_{\mathrm{p}}} s+1}{\left(C_{\mathrm{g} 1}+C_{\mathrm{g} 2}\right) s\left[L\left(C_{\mathrm{p}}+\frac{C_{\mathrm{g} 1} C_{\mathrm{g} 2}}{C_{\mathrm{g} 1}+C_{\mathrm{g} 2}}\right) s^{2}+\frac{L}{R_{\mathrm{p}}} s+1\right]} $ | (2) |
式中:L——定子绕组电感;
Cp——定子绕组的匝间电容;
Cg1+Cg2——定子绕组与铁心之间的杂散电容;
s——复变量;
Rp——高频涡流引起的绕组损耗。
2 FrFT-CNN方法
2.1 FrFT
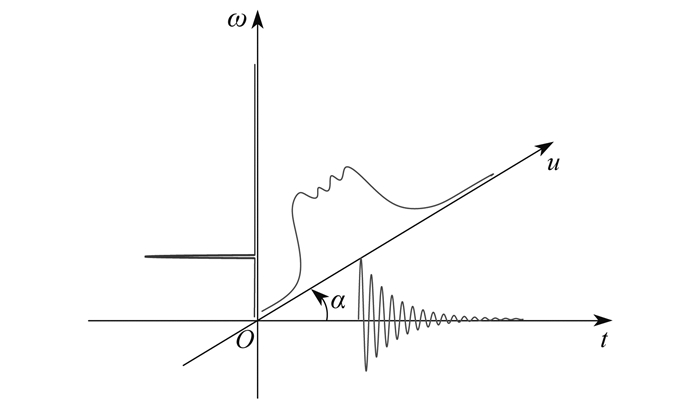
FrFT可以看作传统快速傅里叶变换(Fast Fourier Transform,FFT)的广义形式,FFT代表从时域到频域的单一变换,而FrFT代表时域到频域之间的中间区域的一系列变换。这部分中间区域被称为分数域U。开关振荡电流的时域、频域和分数域示意如图 2所示。其中,t为时间,ω为频率,u为分数阶频率。FrFT可以看成将信号从t轴逆时针旋转角度α到u轴上。本质上,FrFT作为一种时频分析方法,信号可以在分数域U上展示出从时域到频域过程中的全部特征。
FrFT的输出Xα (u)公式如下:
| $ \begin{equation*} X_{\alpha}(u)=\left\{F^{\alpha}[x(t)]\right\}(u)=\int_{-\infty}^{\infty} x(t) K_{\alpha}(t, u) \mathrm{d} t \end{equation*} $ | (3) |
式中:
令
| $ K_{\alpha}(t, u)=\left\{\begin{array}{l} \delta(t, u), \alpha \neq n \pi, n \in \mathbf{Z} \\ \delta(t+u, u), \alpha=n \pi, n \in \mathbf{Z} \\ \delta(t-u, u), \alpha=(2 n \pm 1) \pi, n \in \mathbf{Z} \end{array}\right. $ | (4) |
其中,FrFT变换的旋转角度α = pπ/2,p是阶数,表示变换域相对于时间轴的旋转角度是90°的小数倍。
FrFT的变换存在周期性,反映到信号图像上即为对称性,因此本文只讨论pϵ[0, 1]的变换阶数。p=0阶时,FrFT即表现为时域,p=1阶时,FrFT即为传统的傅里叶变换。
本文尝试利用FrFT,使得信号在分数域内展现出许多时域和频域不存在的特征,利用这些特征来分辨匝绝缘劣化程度,以达到提高状态监测灵敏度的效果。
2.2 CNN
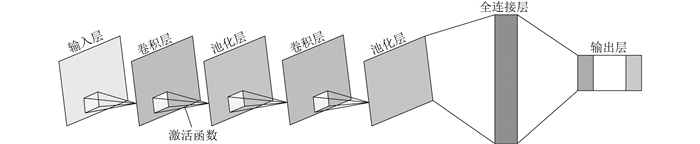
CNN的设计灵感源自于哺乳动物视觉皮层的神经元对特定视觉刺激区域的反应机理。在CNN中,这种反应模式通过运用小型且可重复应用的卷积核得以实现。这些卷积核在输入数据的全域内滑动,负责提取局部特征,并渐进地构建对整体数据的理解。一般而言,CNN的结构包含输入层、卷积层、激活函数、池化层、全连接层以及输出层[17]。CNN的基本结构如图 3所示。
卷积层,作为CNN的核心部分,通过运用卷积核从原始输入数据中提取关键特征。一般而言,卷积层的输入与输出均呈现多通道的特性,每个通道均可被视为一个特征。在实际应用中倾向于选择尺寸较小的卷积核,因为卷积核的尺寸与运算量之间存在正比关系,使用较小的卷积核可以有效降低计算量。卷积操作的计算方法如下:
| $\begin{equation*} y_{j}^{l}=f\left(\sum\limits_{i \in M_{j}} x_{i}^{(l-1)} * w_{i j}^{l}+b_{j}^{l}\right) \end{equation*} $ | (5) |
式中:
f (·)——激活函数;
i——图的编号;
Mj——连接到第j层的特征图的数量;
*——卷积算子;
CNN中的池化层,又称为下采样层,其主要功能在于降低特征图的维度以及减少数据的空间尺寸,进而实现运算量的优化。该层通常紧随连续的卷积层之后,其操作也有助于防止过拟合现象的发生。其公式为
| $ \begin{equation*} z_{j}^{l}=\operatorname{pooling}\left(y_{j}^{l}\right) \end{equation*} $ | (6) |
式中:
pooling()——池化算子。
CNN具备卓越的分类及自适应学习能力,能够有效挖掘匝绝缘劣化特征中的潜在规律,实现对不同劣化状态的辨识,以达到对电机匝绝缘劣化状态的有效监测。
2.3 CM系统和流程
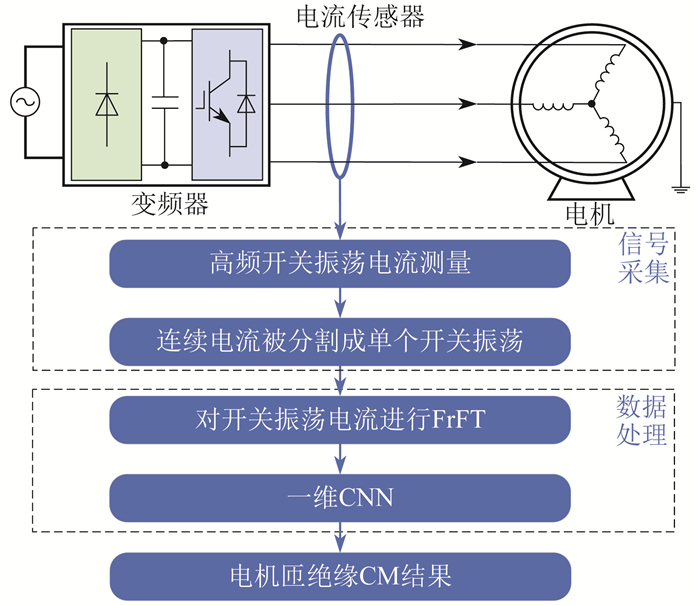
电机匝绝缘CM系统和流程如图 4所示。具体流程如下。
(1) 信号采集。首先是利用高频电流传感器对高频开关振荡电流进行精确测量,随后将所采集的信号进行分割,以获取单个振荡形态。
(2) 数据处理。应用FrFT-CNN算法对多组独立振荡信号进行FrFT,并将这些经过变换的信号输入至设计的一维CNN中,最后网络输出电机匝绝缘CM结果。
3 实验结果与分析
3.1 实验系统
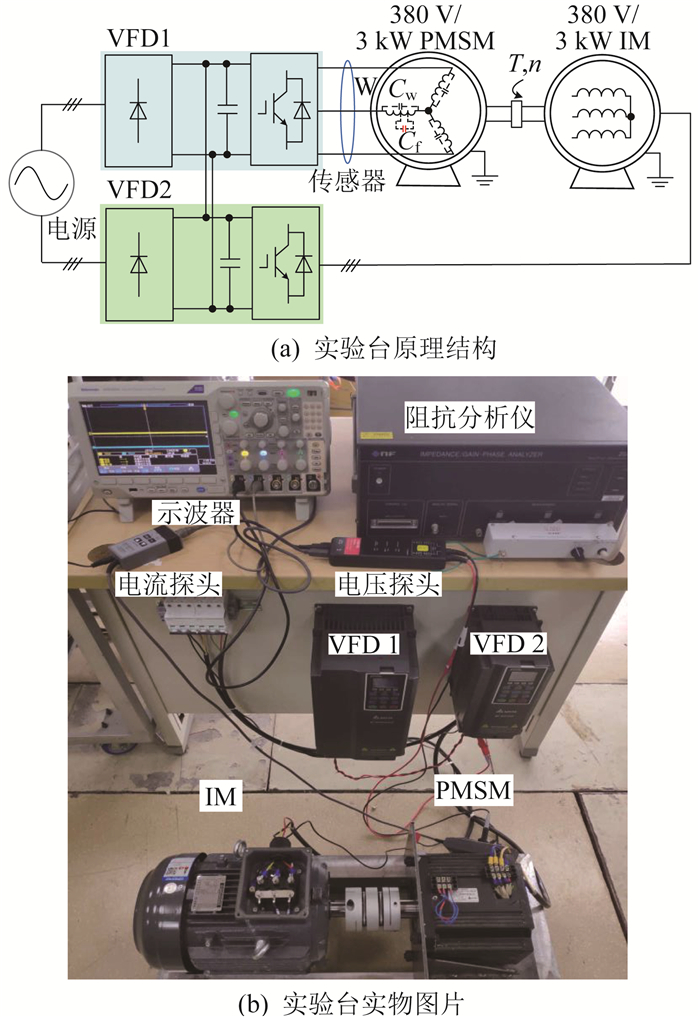
电机匝绝缘CM实验台原理结构及实物图片如图 5所示。
被测机器是额定电流为7.5 A的三相380 V/3 kW永磁同步电机(Permanent Magnet Synchronous Motor,PMSM)。负载机器是一台三相380 V/3 kW感应电机(Induction motor,IM)。表 1列出了PMSM主要参数。
表 1
PMSM的主要参数
| 参数 | 额定电压/V | 额定电流/A | 额定转速/(r/min) | 额定转矩/(N∙m) |
| 数值 | 380 | 7.5 | 1 500 | 19 |
2个变频驱动器(Variable Frequency Drive,VFD)分别用于速度模式和转矩模式下控制PMSM和IM。这一功能使PMSM能够在多种预设条件下进行测试。通过并联2个VFD直流母线,实验期间的有功功率流主要在2个母线之间分配。这种配置对于容量有限的实验室尤为有利。实验中电压探头和电流探头分别为DP6150A高频电压探头(1 500 V/100 MHz)和CP8030B高频电流探头(30 A/50 MHz)。
电机绝缘树脂是具有F级绝缘强度的聚酯酰亚胺材料。绝缘劣化导致相对电容增加20%~ 50%[18]。为了模拟电机绕组匝绝缘的早期绝缘劣化,实验中在2个绕组抽头之间并联了1个小电容器。电机定子绕组的匝间电容Cp约为625.8 pF。在实验中,从PMSM定子的W相绕组线圈中引出2个外部测试抽头,使用0.33 nF和1 nF的并联电容器Cf来模拟变频电机的匝绝缘劣化。实验中不同外加Cf下PMSM提取参数如表 2所示。
表 2
不同外加Cf下PMSM提取参数
| Cf /pF | ∆Cp/pF | (∆Cp/Cp)/% |
| 0 | 0 | 0 |
| 330 | 55.42 | 8.86 |
| 1 000 | 140.18 | 22.40 |
3.2 FrFT-CNN实验结果分析
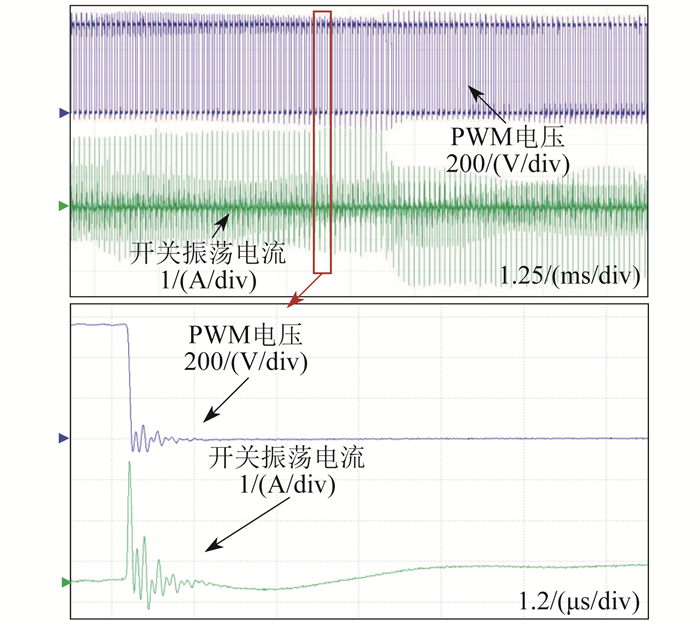
图 6显示了PMSM正常运行时的PWM电压和开关振荡电流波形。因此,这有助于将采样的时间序列信号分成几个不同的采样,每个采样对应一个单独的振荡单元。每段时间跨度为10 μs,包含1 000个采样点。每种绝缘状态有500个采样作为数据样本。
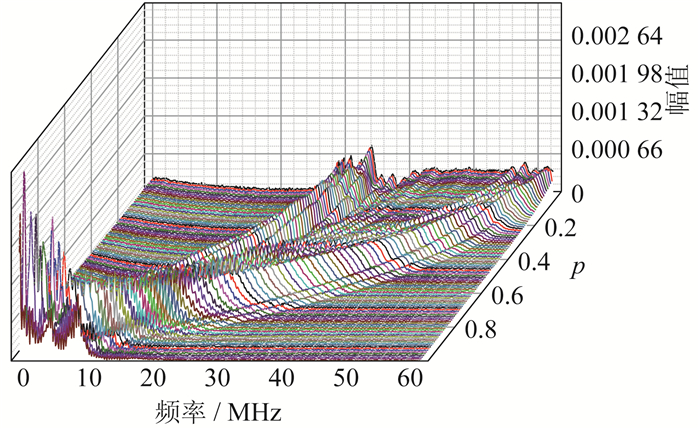
本文使用Python对实验数据执行FrFT-CNN算法。单个开关振荡的分数阶傅里叶频谱如图 7所示。开关振荡电流在时频域的分数阶傅里叶频谱上表现出许多不同特征。
本文设计了一种针对变频电机匝绝缘CM的一维CNN模型。网络模型结构参数如表 3所示。该模型将包含3 003个数据点的高频开关振荡电流作为输入,高频开关振荡电流采用经过FrFT预处理后的数据。在卷积层中,采用64×1和3×1这2种尺寸的卷积核,并选用LReLU函数作为激活函数。
表 3
网络模型结构参数
| 网络层 | 卷积核大小 | 步长 | 卷积核数目 | 激活函数 | 输出维度 |
| 输入层 | 3 003×1 | ||||
| 卷积层1 | 64×1 | 16×1 | 16 | LReLU | 188×16 |
| 池化层1 | 2×1 | 2×1 | 16 | 94×16 | |
| 卷积层2 | 3×1 | 2×1 | 32 | LReLU | 47×32 |
| 池化层2 | 2×1 | 2×1 | 32 | 24×32 | |
| 卷积层3 | 3×1 | 2×1 | 64 | LReLU | 12×64 |
| 池化层3 | 2×1 | 2×1 | 64 | 6×64 | |
| 全连接层 | LReLU | 64×1 | |||
| 输出层 | Softmax | 3×1 |
在实验过程中,首先将数据自动划分为训练集和测试集,其中训练集占比70%,测试集占比30%。本文设定了3种不同的匝绝缘状态,分别为健康状态、早期劣化状态和中度劣化状态。每种状态均包含500个样本,每个样本包含3 003个连续数据点。实验数据说明见表 4。
表 4
实验数据说明
| 状态 | Cf/pF | 标签 |
| 健康 | 0 | C1 |
| 早期劣化 | 330 | C2 |
| 中度劣化 | 1 000 | C3 |
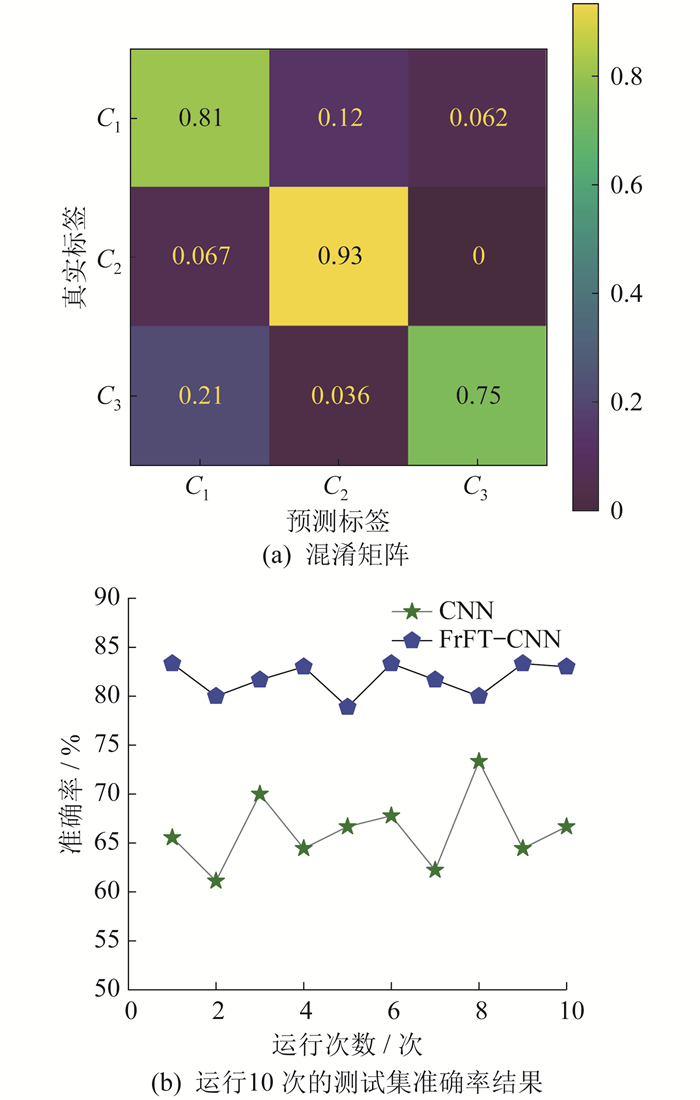
电机匝绝缘CM结果如图 8所示。矩阵的对角线元素表示每种匝绝缘劣化状态的监测精度。
由图 8(a)可知,该模型在识别精度上维持在83% 左右的水平,并展现出较稳定的状态。但值得注意的是,对于本文重点关注的早期劣化状态,该模型的整体准确率可以达到93%。由图 8(b) 可知,采用FrFT-CNN方法在10次运行后可稳定达到80%以上的准确率,相比于采用CNN方法准确率有了明显的提升,且模型更具稳定性,体现出FrFT可以更好展现匝绝缘劣化特征,而本文设计的FrFT-CNN方法可以更有效监测电机匝绝缘劣化状态。鉴于当前在电机匝绝缘状态监测领域中,针对深度学习的相关研究尚属稀缺,因此本文在初步探索将深度学习技术应用于变频电机匝绝缘状态监测可行性的基础上,为后续研究做了一些基础性工作。
4 结论
本文主要针对电机匝绝缘劣化特性微弱的问题,提出了一种变频电机匝绝缘CM新方法。通过理论与实验研究,可以得到如下结论。
(1) FrFT能够揭示电机匝绝缘劣化的更多细节特征。
(2) FrFT-CNN的电机匝绝缘CM方法准确率可以稳定在80% 以上,相比于CNN方法,具有准确性高和稳定性良好的优点。此外,将深度学习引入电机匝绝缘CM领域,为后续研究提供了一种新思路。以后还会继续改进文中的CNN模型,进一步提高模型准确率以达到实际应用水平。
参考文献
-
[1]FANG B M, QIU W Q, WANG M C, et al. Evaluation index system of shared energy storage market towards renewable energy accommodation scenario: a China's Qinghai province context[J]. Global Energy Interconnection, 2022, 5(1): 77-95. DOI:10.1016/j.gloei.2022.04.007
-
[2]THOMAS V, KUMARAVEL S, ASHOK S. Fuzzy controller-based self-adaptive virtual synchronous machine for microgrid application[J]. IEEE Transactions on Energy Conversion, 2021, 36(3): 2427-2437. DOI:10.1109/TEC.2021.3057487
-
[3]李豪, 刘静宇, 向大为, 等. 基于差模开关振荡的变频电机绕组相端绝缘状态特征提取与解耦[J]. 中国电机工程学报, 2024, 44(4): 1608-1618.
-
[4]PALAVICINO P C, SARLIOGLU B. Estimation of position and shorted turns percentage of an inter-turn short circuit in interior permanent magnet synchronous machines based on a current observer and stationary reference frame tracking[J]. IEEE Transactions on Industry Applications, 2023, 59(4): 4066-4075. DOI:10.1109/TIA.2023.3268996
-
[5]NIU G, DONG X, CHEN Y J. Motor fault diagnostics based on current signatures: a review[J]. IEEE Transactions on Instrumentation and Measurement, 2023, 72: 3520919.
-
[6]郑大勇, 张品佳. 交流电机定子绝缘故障诊断与在线监测技术综述[J]. 中国电机工程学报, 2019, 39(2): 395-406.
-
[7]NETI P, GRUBIC S. Online broadband insulation spectroscopy of induction machines using signal injection[J]. IEEE Transactions on Industry Applications, 2017, 53(2): 1054-1062. DOI:10.1109/TIA.2016.2639014
-
[8]CAO S R, NIU F, HUANG X Y, et al. Time-frequency characteristics research of common mode current in PWM motor system[J]. IEEE Transactions on Power Electronics, 2020, 35(2): 1450-1458. DOI:10.1109/TPEL.2019.2916686
-
[9]NUSSBAUMER P, VOGELSBERGER M A, WOLBANK T M. Induction machine insulation health state monitoring based on online switching transient exploitation[J]. IEEE Transactions on Industrial Electronics, 2015, 62(3): 1835-1845. DOI:10.1109/TIE.2014.2361114
-
[10]李豪, 赵孟, 向大为, 等. 基于开关瞬态频率响应的伺服电机早期匝绝缘劣化在线监测[J]. 中国电机工程学报, 2020, 40(10): 3359-3367.
-
[11]XIANG D W, LI H, YAN H, et al. Online monitoring of incipient turn insulation degradation for inverter-fed machine using sensitive tail component in PWM switching oscillations[J]. IEEE Transactions on Power Electronics, 2021, 36(8): 8730-8742. DOI:10.1109/TPEL.2021.3049809
-
[12]HE S F, TIAN W, ZHANG J M, et al. A high efficient approach for power disturbance waveform compression in the view of heisenberg uncertainty[J]. IEEE Transactions on Industrial Informatics, 2019, 15(5): 2580-2591. DOI:10.1109/TII.2018.2868732
-
[13]ŞAHINUÇ F, KOÇ A. Fractional Fourier transform meets transformer encoder[J]. IEEE Signal Processing Letters, 2022, 29: 2258-2262. DOI:10.1109/LSP.2022.3217975
-
[14]XIE C X, ZHANG L M, ZHONG Z G. Quasi-LFM radar waveform recognition based on fractional Fourier transform and time-frequency analysis[J]. Journal of Systems Engineering and Electronics, 2021, 32(5): 1130-1142. DOI:10.23919/JSEE.2021.000097
-
[15]WANG H, LIU Z L, PENG D D, et al. Understanding and learning discriminant features based on multiattention 1DCNN for wheelset bearing fault diagnosis[J]. IEEE Transactions on Industrial Informatics, 2020, 16(9): 5735-5745. DOI:10.1109/TII.2019.2955540
-
[16]GANDHI A, CORRIGAN T, PARSA L. Recent advances in modeling and online detection of stator interturn faults in electrical motors[J]. IEEE Transactions on Industrial Electronics, 2011, 58(5): 1564-1575. DOI:10.1109/TIE.2010.2089937
-
[17]钱刚. 基于嵌入式人工智能算法的电机故障在线诊断研究[D]. 合肥: 安徽大学, 2020.
-
[18]LI H, XIANG D W, YANG X W, et al. Compressed sensing method for IGBT high-speed switching time on-line monitoring[J]. IEEE Transactions on Industrial Electronics, 2019, 66(4): 3185-3195. DOI:10.1109/TIE.2018.2847647