|
|
|
发布时间: 2024-10-28 |
智能设备 |
|
|
|
收稿日期: 2024-03-18
中图法分类号: TM301.2
文献标识码: A
文章编号: 2096-8299(2024)05-0475-09
|
摘要
针对双三相永磁同步电机在传统矢量控制中电流脉动较大的问题,提出了一种基于电压矢量合成原理的多矢量模型预测电流控制策略。首先,通过结合双dq解耦变换与三相解耦脉宽调制(PWM)算法,将电机的每组三相绕组视为基本单元。其次,在每个控制扇区内,通过选择2个有效电压矢量和1个零矢量,构造出所需的目标电压矢量,并将其纳入备选电压矢量集,以实现任意方向和幅值的电压覆盖。最后,采用dq轴电流的无差拍算法确定各矢量的作用时间。仿真结果表明,所提控制策略显著降低了电流脉动,增强了系统稳定性。
关键词
双三相永磁同步电机; 电流脉动; 模型预测电流控制; 矢量作用时间
Abstract
Aiming at the problem of large current ripple in traditional vector control of dual three-phase permanent magnet synchronous motor, this paper proposes a multi-vector model predictive current control strategy based on voltage vector synthesis principle. Firstly, this method regards each group of three-phase windings of the motor as a basic unit by combining dual dq decoupling transformation with three-phase decoupling pulse-width modulation (PWM) algorithm. Secondly, in each control sector, by selecting two effective voltage vectors and a zero vector, the required target voltage vector is constructed and incorporated into the set of alternative voltage vectors to achieve voltage coverage in any direction and amplitude. Finally, the deadbeat algorithm of dq axis current is used to determine the action time of each vector. The simulation results show that the proposed control strategy significantly reduces the current ripple and enhances the system stability.
Key words
dual three-phase permanent magnet synchronous motor; current ripple; model predictive current control; vector action time
近年来,随着科技的快速进步,电动汽车、船舶以及航空航天等领域对调速系统的功率和可靠性要求持续升高。相较于传统的三相永磁同步电机,多相永磁同步电机凭借其更小的转矩脉动、更强的容错能力以及更高的功率密度,展现出更加广泛的应用潜力[1-4]。由于与传统三相电机紧密关联,相移30°的双三相电机在多相电机中受到了广泛关注。
在双三相永磁同步电机(Double Three PhasePermanent Magnet Synchronous Motor,DTPPMSM)控制领域,对电机模型进行解耦是控制的前提。目前,双三相电机有两种解耦变换方法:一种是双dq坐标变换[5-6],另一种则是矢量空间解耦变换[7-8]。对DTP-PMSM的控制研究大部分基于矢量解耦变换理论,而对基于双dq坐标变换的控制研究较少。有限集模型预测控制(Finite Control Set-Model Predictive Control,FCS-MPC) 因其出色的动态反应速度和对非线性约束的灵活处理能力在电机领域广受关注。DTP-PMSM的逆变器为模型预测控制提供了大量的电压矢量资源,但也带来大量的计算量[9-11]。文献[12]将DTP-PMSM的基波和谐波电流误差引入成本函数,并从64个电压空间矢量中筛选出特定的一组矢量用于模型预测控制。此方法在降低计算复杂度上取得了一定成效,但这种方式可能会忽略最优矢量,进而影响电流控制的效果。文献[13]使用一种计及死区模型预测控制的方法,通过一种新的合成矢量方法减少了计算负担,同时有效抑制了谐波电流,但是并未将转矩和电流的波动问题考虑在内。文献[14]为了消除传统模型预测控制中复杂的权重系数,提出了一种由两个隔离电源供电的开式绕组永磁同步电机系统的简化模型预测控制,并引入了一种开关状态分布策略,以降低双逆变器的开关频率,但是算法的复杂性和对特定硬件的依赖可能会限制其应用范围。文献[15]采用了一种利用虚拟电压矢量实现低共模电压的预测电流控制策略,该方法通过两次预测和合成矢量来抑制共模电压并降低谐波电流,虽然其控制性能在很大程度上依赖于电机和系统模型的准确性,但是通过合成虚拟矢量的思路减少了控制算法的复杂度。文献[16]采用了一种针对所选优化矢量的占空比调整方法,有效降低了磁链和转矩脉动,同时确保了开关频率的恒定。但在模型预测扭矩控制过程中,因磁链和转矩幅值具有不同的度量单位,必须在成本函数中加入权重因子,这给算法的应用带来了困难。
本文以DTP-PMSM为研究对象,提出了一种多矢量模型预测电流控制方法。首先,对DTPPMSM的双dq坐标变换下的离散数学模型进行求解,得出电流预测公式;其次,结合双三相电机的三相解耦脉宽调制(Pulse-Width Modulation,PWM算法将DTP-PMSM的六相电压源逆变器控制转化成2套三相电压源逆变器控制;然后,再在每个扇区对2个有效矢量和零矢量进行期望电压矢量的合成;最后,根据电流无差拍方法计算各矢量作用时间,并通过仿真验证所提方法的有效性和可行性。
1 离散数学模型的建立
DTP-PMSM拥有2套三相对称绕组。这2套绕组在理论分析中可被视作2个独立的三相永磁电机系统的集成。为了简化和分析这一复合电机系统,可以对每个独立的子系统单独应用传统的三相电机坐标进行变换。通过这种方式,可以构建一个六相变换矩阵,该矩阵实质上由2个相位角差为30°的Clarke-Park变换矩阵组成。该六相变换矩阵P可表示为
| $ \boldsymbol{P}=\left[\begin{array}{ll} \boldsymbol{P}_{1} & \\ & \boldsymbol{P}_{2} \end{array}\right] $ | (1) |
| $ \boldsymbol{P}_{1}=\frac{2}{3}\left[\begin{array}{ccc}\cos \theta & \cos \left(\theta-\frac{2 \pi}{3}\right) & \cos \left(\theta+\frac{2 \pi}{3}\right) \\ -\sin \theta & -\sin \left(\theta-\frac{2 \pi}{3}\right) & -\sin \left(\theta+\frac{2 \pi}{3}\right) \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2}\end{array}\right] $ | (2) |
| $\boldsymbol{P}_{2}=\left[\begin{array}{ccc}\cos \left(\theta-\frac{\pi}{6}\right) & \cos \left(\theta-\frac{5 \pi}{6}\right) & \cos \left(\theta+\frac{\pi}{2}\right) \\ -\sin \left(\theta-\frac{\pi}{6}\right) & -\sin \left(\theta-\frac{5 \pi}{6}\right) & -\sin \left(\theta+\frac{\pi}{2}\right) \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2}\end{array}\right] $ | (3) |
式中:θ——转子磁极位置与a相绕组轴线之间的电角度。
将所提出的变换矩阵应用于初始电压方程并去除零序分量后,可以得到新的以各绕组的dq轴分量为变量的磁链方程:
| $ \left[\begin{array}{l} \psi_{d 1} \\ \psi_{q 1} \\ \psi_{d 2} \\ \psi_{q 2} \end{array}\right]=\left[\begin{array}{cccc} L_{d} & 0 & L_{d 1} & 0 \\ 0 & L_{q} & 0 & L_{q 1} \\ L_{d 1} & 0 & L_{d} & 0 \\ 0 & L_{q 1} & 0 & L_{q} \end{array}\right]\left[\begin{array}{l} i_{d 1} \\ i_{q 1} \\ i_{d 2} \\ i_{q 2} \end{array}\right]+\left[\begin{array}{l} 1 \\ 0 \\ 1 \\ 0 \end{array}\right] \psi_{\mathrm{f}} $ | (4) |
式中:
ψf——永磁体磁链。
其中,
| $\left\{\begin{array}{l} L_{d}=1.5 L_{\text {aa}d}+L_{\text {aal }} \\ L_{q}=1.5 L_{\text {aa} q}+L_{\text {aal }} \\ L_{d 1}=1.5 L_{\text {aa}d} \\ L_{q 1}=1.5 L_{\text {aa} q} \end{array}\right. $ | (5) |
式中:
Laal——漏感。
电磁转矩Te公式为
| $ \begin{equation*} T_{\mathrm{e}}=\frac{3}{2} p_{0}\left(i_{q 1} \psi_{d 1}-i_{d 1} \psi_{q 1}+i_{q 2} \psi_{d 2}-i_{d 2} \psi_{q 2}\right) \end{equation*} $ | (6) |
式中:p0——极对数。
文献[17]对DTP-PMSM的基于矢量空间解耦和双dq坐标变换解耦的矢量控制进行对比,当2套绕组的d轴电流环和q轴电流环采用相同控制参数时,式(4)可表示为
| $ \left[\begin{array}{l} \psi_{d 1} \\ \psi_{q 1} \\ \psi_{d 2} \\ \psi_{q 2} \end{array}\right]=\left[\begin{array}{cccc} L_{\mathrm{D}} & 0 & 0 & 0 \\ 0 & L_{\mathrm{Q}} & 0 & 0 \\ 0 & 0 & L_{\mathrm{D}} & 0 \\ 0 & 0 & 0 & L_{\mathrm{Q}} \end{array}\right]\left[\begin{array}{c} i_{d 1} \\ i_{q 1} \\ i_{d 2} \\ i_{q 2} \end{array}\right]+\left[\begin{array}{l} 1 \\ 0 \\ 1 \\ 0 \end{array}\right] \psi_{\mathrm{f}} $ | (7) |
| $ 其中:~~~~~ \left\{\begin{array}{l} L_{\mathrm{D}}=L_{d}+L_{d 1} \\ L_{\mathrm{Q}}=L_{q}+L_{q 1} \end{array}\right. $ | (8) |
据此分析,电流控制器的设计可以直接基于矢量空间解耦模型中的dq子空间参数,无须依赖复杂的解耦计算过程。这样的设计策略可以实现与传统三相电机相同的控制性能,从而简化控制逻辑并保持系统的高效性。在此基础上,可以得到双dq变换下DTP-PMSM的状态方程为
| $ \begin{align*} {\left[\begin{array}{c} \frac{\mathrm{d} i_{d 1}}{\mathrm{~d} t} \\ \frac{\mathrm{~d} i_{q 1}}{\mathrm{~d} t} \end{array}\right]=} & {\left[\begin{array}{cc} -\frac{R}{L_{\mathrm{D}}} & \omega_{\mathrm{e}} \frac{L_{\mathrm{Q}}}{L_{\mathrm{D}}} \\ -\omega_{\mathrm{e}} \frac{L_{\mathrm{D}}}{L_{\mathrm{Q}}} & -\frac{R}{L_{\mathrm{Q}}} \end{array}\right]\left[\begin{array}{c} i_{d 1} \\ i_{q 1} \end{array}\right]+\left[\begin{array}{cc} \frac{1}{L_{\mathrm{D}}} & 0 \\ 0 & \frac{1}{L_{\mathrm{Q}}} \end{array}\right] \times } \\ & {\left[\begin{array}{l} u_{d 1} \\ u_{q 1} \end{array}\right]+\left[\begin{array}{c} 0 \\ -\frac{\psi_{\mathrm{f}}}{L_{\mathrm{Q}}} \omega_{\mathrm{e}} \end{array}\right] } \end{align*} $ | (9) |
| $\begin{aligned} {\left[\begin{array}{c} \frac{\mathrm{d} i_{d 2}}{\mathrm{~d} t} \\ \frac{\mathrm{~d} i_{q 2}}{\mathrm{~d} t} \end{array}\right]=} & {\left[\begin{array}{cc} -\frac{R}{L_{\mathrm{D}}} & \omega_{\mathrm{e}} \frac{L_{\mathrm{Q}}}{L_{\mathrm{D}}} \\ -\omega_{\mathrm{e}} \frac{L_{\mathrm{D}}}{L_{\mathrm{Q}}} & -\frac{R}{L_{\mathrm{Q}}} \end{array}\right]\left[\begin{array}{cc} i_{d 2} \\ i_{q 2} \end{array}\right]+\left[\begin{array}{cc} \frac{1}{L_{\mathrm{D}}} & 0 \\ 0 & \frac{1}{L_{\mathrm{Q}}} \end{array}\right] \times } \\ & {\left[\begin{array}{l} u_{d 2} \\ u_{q 2} \end{array}\right]+\left[\begin{array}{c} 0 \\ -\frac{\psi_{\mathrm{f}}}{L_{\mathrm{Q}}} \omega_{\mathrm{e}} \end{array}\right] } \end{aligned} $ | (10) |
式中:R——定子电阻;
ωe——转子电角速度;
ud1,uq1——第1套绕组定子电压的d轴和q轴分量;
ud2,uq2——第2套绕组定子电压的d轴和q轴分量。
根据文献[18]对离散化状态方程进行求解,得到当采样时间T足够小时,离散化的
| $ \left[\begin{array}{c}\frac{\mathrm{d} i_{d 1}}{\mathrm{~d} t} \\ \frac{\mathrm{~d} i_{q 1}}{\mathrm{~d} t}\end{array}\right]=\left[\begin{array}{cc}1-\frac{T R}{L_{\mathrm{D}}} & T \omega_{\mathrm{e}}(k) \\ -T \omega_{\mathrm{e}}(k) & 1-\frac{T R}{L_{\mathrm{Q}}}\end{array}\right]\left[\begin{array}{l}i_{d 1} \\ i_{q 1}\end{array}\right]+\\ \left[\begin{array}{cc}\frac{T}{L_{\mathrm{D}}} & 0 \\ 0 & \frac{T}{L_{\mathrm{Q}}}\end{array}\right]\left[\begin{array}{l}u_{d 1} \\ u_{q 1}\end{array}\right]+\left[\begin{array}{c}0 \\ -\frac{T \psi_{\mathrm{f}}}{L_{\mathrm{Q}}} \omega_{\mathrm{e}}(k)\end{array}\right] $ | (11) |
| $ \left[\begin{array}{c}\frac{\mathrm{d} i_{d 2}}{\mathrm{~d} t} \\ \frac{\mathrm{~d} i_{q 2}}{\mathrm{~d} t}\end{array}\right]=\left[\begin{array}{cc}1-\frac{T R}{L_{\mathrm{D}}} & T \omega_{\mathrm{e}}(k) \\ -T \omega_{\mathrm{e}}(k) & 1-\frac{T R}{L_{\mathrm{Q}}}\end{array}\right]\left[\begin{array}{c}i_{d 2} \\ i_{q 2}\end{array}\right]+$ $\left[\begin{array}{cc}\frac{T}{L_{\mathrm{D}}} & 0 \\ 0 & \frac{T}{L_{\mathrm{Q}}}\end{array}\right]\left[\begin{array}{l}u_{d 2} \\ u_{q 2}\end{array}\right]+\left[\begin{array}{c}0 \\ -\frac{T \psi_{\mathrm{f}}}{L_{\mathrm{Q}}} \omega_{\mathrm{e}}(k)\end{array}\right] $ | (12) |
式中:ωe (k)——采样时刻k时的转子电角速度。
由此可得,离散的电流预测公式为
| $ \left\{\begin{array}{l}i_{d i}(k+1)=i_{d i}(k)+\frac{T}{L_{\mathrm{D}}}\left[u_{d i}(k)-R i_{d i}(k)+E_{d i}(k)\right], i=1, 2 \\ i_{q i}(k+1)=i_{q i}(k)+\frac{T}{L_{\mathrm{Q}}}\left[u_{q i}(k)-R i_{q i}(k)+E_{q i}(k)\right], i=1, 2\end{array}\right. $ | (13) |
| $其中:\quad\left\{\begin{array}{l}E_{d i}(k)=\omega_{\mathrm{e}}(k) L i_{q i}(k) \\ E_{q i}(k)=-\omega_{\mathrm{c}}(k) L i_{q i}(k)-\omega_{\mathrm{c}}(k) \psi_{\mathrm{f}}\end{array}\right. $ | (14) |
式中:
2 多矢量模型预测电流控制策略
2.1 三相解耦PMW算法
文献[19]分析得出双三相电机在2个α-β子空间中的电压矢量和2套三相绕组电压矢量的对应关系为
| $ \left\{\begin{array}{l} \boldsymbol{U}_{1}=\boldsymbol{U}_{\alpha \beta}+\boldsymbol{U}_{x y}^{*} \\ \boldsymbol{U}_{2}=\mathrm{e}^{-{\rm{j}} 30°}\left(\boldsymbol{U}_{\alpha \beta}-\boldsymbol{U}_{x y}^{*}\right) \end{array}\right. $ | (15) |
式中:U1——第1套三相绕组对应逆变器的电压矢量;
U2——第2套三相绕组对应逆变器的电压矢量;
Uαβ——α-β子空间中的电压矢量;
在式(15)中,将
2.2 多矢量模型预测电流控制原理
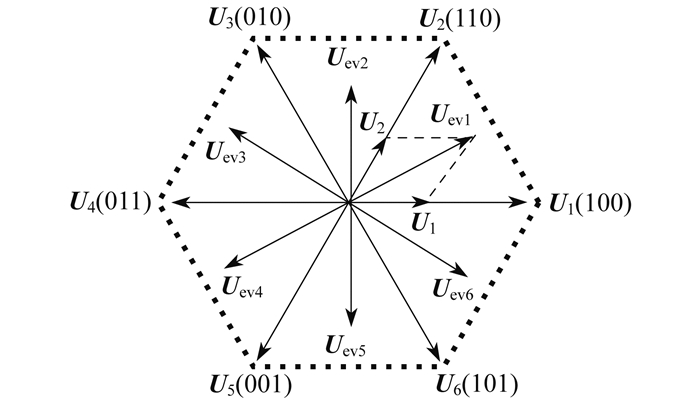
本文提出的多矢量模型预测电流控制策略,在电压空间矢量图的每个扇区内,结合2个相邻的有效(非零)电压矢量以及1个零电压矢量,实现了期望电压矢量在方向和幅值上的灵活调控。以DTPPMSM的1套绕组为例,在6个扇区内可分别构造出6个期望电压矢量。期望电压矢量合成见表 1。
表 1
期望电压矢量合成
| 扇区 | 两个有效电压矢量 | 零电压矢量 | 期望电压矢量 |
| 1 | U1 , U2 | U0(U7) | Uev1 |
| 2 | U2,U3 | U0 (U7) | Uev2 |
| 3 | U3,U4 | U0(U7) | Uev3 |
| 4 | U4,U5 | U0(U7) | Uev4 |
| 5 | U5,U6 | U0(U7) | Uev5 |
| 6 | U6,U1 | U0(U7) | Uev6 |
在确定了基本电压矢量之后,接下来需要对电压矢量的作用时间进行分配,以便合成期望电压矢量。根据式(9)和式(10),零电压矢量作用即
| $ \begin{cases}s_{d i 0}=-\frac{R i_{d i}}{L_{\mathrm{D}}}+\frac{\omega_{\mathrm{c}} L_{\mathrm{Q}} i_{q i}}{L_{\mathrm{D}}}, & i=1, 2 \\ s_{q i 0}=-\frac{R i_{q i}}{L_{\mathrm{Q}}}-\frac{\omega_{\mathrm{c}} L_{\mathrm{D}} i_{d i}}{L_{\mathrm{Q}}}-\frac{\omega_{\mathrm{e}} \psi_{\mathrm{f}}}{L_{\mathrm{Q}}}, & i=1, 2\end{cases} $ | (16) |
式中:
当2个相邻的有效电压矢量Uo和Up作用时,dq轴电流的斜率为
| $ \left\{\begin{array}{l} s_{d i \mathrm{o}}=\left.\frac{\mathrm{d} i_{d i}}{\mathrm{~d} t}\right|_{u_{d i}=u_{d i \mathrm{o}}}=s_{d i 0}+\frac{u_{d i \mathrm{o}}}{L_{\mathrm{D}}}, i=1,2 \\ S_{q i \mathrm{o}}=\left.\frac{\mathrm{d} i_{q i}}{\mathrm{~d} t}\right|_{u_{q i}=u_{q i \mathrm{o}}}=S_{q i 0}+\frac{u_{q i \mathrm{o}}}{L_{\mathrm{Q}}}, i=1,2 \\ S_{d i \mathrm{p}}=\left.\frac{\mathrm{d} i_{d i}}{\mathrm{~d} t}\right|_{u_{d i}=u_{d i \mathrm{p}}}=s_{d i 0}+\frac{u_{d i \mathrm{p}}}{L_{\mathrm{D}}}, i=1,2 \\ S_{q i \mathrm{p}}=\left.\frac{\mathrm{d} i_{q i}}{\mathrm{~d} t}\right|_{u_{q i}=u_{q i \mathrm{p}}}=s_{q i 0}+\frac{u_{q i \mathrm{p}}}{L_{\mathrm{Q}}}, i=1,2 \end{array}\right. $ | (17) |
式中:
udio,uqio——第i套三相绕组中 Uo作用时d轴和q轴电压分量;
sdip,sqip——第i套三相绕组中 Up作用时d轴和q轴电流的斜率;
udip,uqip——第i套三相绕组中 Up作用时d轴和q轴电压分量。
为实现预测电流与给定值之间的无误差跟踪,本文基于无差拍控制策略来确定电压矢量的作用时长,确保下一时间点的预测电流值与设定目标值相等,dq轴电流预测公式可改写为
| $\begin{cases}i_{d i}(k+1)=i_{d i}(k)+S_{d i \mathrm{o}} t_{\mathrm{o}}+S_{d i \mathrm{p}} t_{\mathrm{p}}+S_{d i 0} t_{\mathrm{z}}=i_{d i}^*, & i=1,2 \\ i_{q i}(k+1)=i_{q i}(k)+S_{q i \mathrm{o}} t_{\mathrm{o}}+S_{q i \mathrm{p}} t_{\mathrm{p}}+S_{q i 0} t_{\mathrm{z}}=i_{q i}^*, & i=1,2\end{cases} $ | (18) |
式中:to,tp,tz——Uo、Up和零电压矢量的作用时间。
3个电压矢量总作用时间为采样周期T,即:
| $ \begin{equation*} T=t_{\mathrm{o}}+t_{\mathrm{p}}+t_{\mathrm{z}} \end{equation*} $ | (19) |
联立式(16)至式(19),有:
| $ \left\{\begin{array}{l} t_{\mathrm{o}}=\frac{\left[i_{d i}^{*}-i_{d i}(k)\right]\left(s_{q i \mathrm{p}}-s_{q i 0}\right)+\left[i_{q i}^{*}-i_{q i}(k)\right]\left(s_{d i 0}-s_{d i \mathrm{p}}\right)+T\left(s_{q i 0} s_{d i \mathrm{p}}-s_{q i \mathrm{i}} s_{d i 0}\right)}{s_{q i 0} s_{d i \mathrm{p}}+s_{q i \mathrm{o}} s_{d i 0}+s_{q i \mathrm{p}} s_{d i \mathrm{o}}-s_{q i \mathrm{o}} s_{d i \mathrm{p}}-s_{q i \mathrm{p}} s_{d i 0}-s_{q i \mathrm{o}} s_{d i \mathrm{o}}}, i=1, 2 \\ t_{\mathrm{p}}=\frac{\left[i_{d i}^{*}-i_{d i}(k)\right]\left(s_{q i 0}-s_{q i \mathrm{o}}\right)+\left[i_{q i}^{*}-i_{q i}(k)\right]\left(s_{d i \mathrm{o}}-s_{d i 0}\right)+T\left(s_{q i \mathrm{o}} s_{d i 0}-s_{q i 0} s_{d \mathrm{o}}\right)}{s_{q i 0} s_{d i \mathrm{p}}+s_{q i \mathrm{o}} s_{d i 0}+s_{q i \mathrm{p}} s_{d i \mathrm{o}}-s_{q i \mathrm{o}} s_{d i \mathrm{p}}-s_{q i \mathrm{p}} s_{d i 0}-s_{q i 0} s_{d i \mathrm{o}}}, i=1, 2 \\ t_{\mathrm{z}}=T-t_{\mathrm{o}}-t_{\mathrm{p}} \end{array}\right. $ | (20) |
根据式(19),to、tp、tz须在0~T范围内,否则,排除此种情况下合成的期望电压矢量。
2.3 期望电压矢量合成
以三相电压源逆变器电压矢量扇区作为研究对象,为了降低开关损耗,选择零矢量作为关键元素。通过合理组合相邻2个有效电压矢量与1个零矢量,在每个扇区内仅生成1个期望电压矢量,从而构建出6个期望电压矢量的完整集合。此方法简化了在线预测过程,因为仅须进行6次预测即可确定最优电压矢量。期望电压矢量合成如图 1所示。
根据式(20),可以计算出期望电压矢量在dq轴上的分量ud、uq,其表达式为
| $ \left\{\begin{array}{l} u_{d}=\frac{t_{\mathrm{o}}}{T} u_{d \mathrm{o}}+\frac{t_{\mathrm{p}}}{T} u_{d \mathrm{p}} \\ u_{q}=\frac{t_{\mathrm{o}}}{T} u_{q \mathrm{o}}+\frac{t_{\mathrm{p}}}{T} u_{q \mathrm{p}} \end{array}\right. $ | (21) |
式中:udo,uqo——Uo作用时d轴和q轴电压分量;udp,uqp——Up作用时d轴和q轴电压分量。
2.4 价值函数
通过设计一个价值函数,以最小化电流矢量跟踪误差为目标,选择最优的虚拟合成电压矢量,以实现对双dq坐标变换下DTP-PMSM的2套三相绕组d轴、q轴电流误差的有效控制。通过计算每个电压矢量对应的价值函数值,可以识别出哪一个电压矢量能够最小化电流跟踪误差,从而实现对电机更加精确的控制。价值函数g的公式如下:
| $ \left\{\begin{array}{l} g=g_{1}+g_{2} \\ g_{1}=\left|i_{q 1}^{*}-i_{q 1}(k)\right|+\left|i_{d 1}^{*}-i_{d 1}(k)\right| \\ g_{2}=\left|i_{q 2}^{*}-i_{q 2}(k)\right|+\left|i_{d 2}^{*}-i_{d 2}(k)\right| \end{array}\right. $ | (22) |
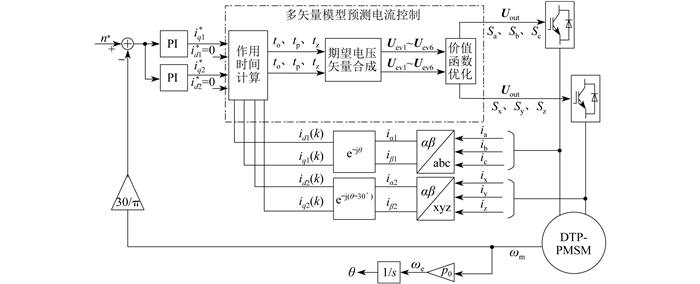
基于双dq坐标变换的DTP-PMSM多矢量模型预测电流控制系统框图如图 2所示。
图 2中:n*为给定转速;Sa,Sb,Sc为第1套三相绕组对应逆变器的开关信号;Sx,Sy,Sz为第2套三相绕组对应逆变器的开关信号;iα1,iβ1为第1套三相绕组相电流经Park变换得到的电流;iα2,iβ2为第3套三相绕组相电流经Park变换得到的电流;ia,ib,ic为第1套三相绕组的相电流;ix,iy,iz为第2套三相绕组的相电流;ωm为转子机械角速度。系统采用id1*=id2*=0,速度环PI(比例积分)控制器的输出指定为q轴电流的预设值,在多矢量模型预测控制模块中,首先基于电流的预设值和反馈值,计算to、tp、tz,用于在各个扇区合成期望电压矢量,最后通过价值函数优化选出最优电压矢量Uout。
3 系统仿真及结果分析
3.1 仿真参数
本文参照MATLAB/Simulink中三相永磁同步电机模型,搭建了DTP-PMSM的仿真控制模型,对所提出的多矢量模型预测电流控制策略进行仿真验证。电机参数为:极对数p0=3,定子电感
3.2 仿真结果分析
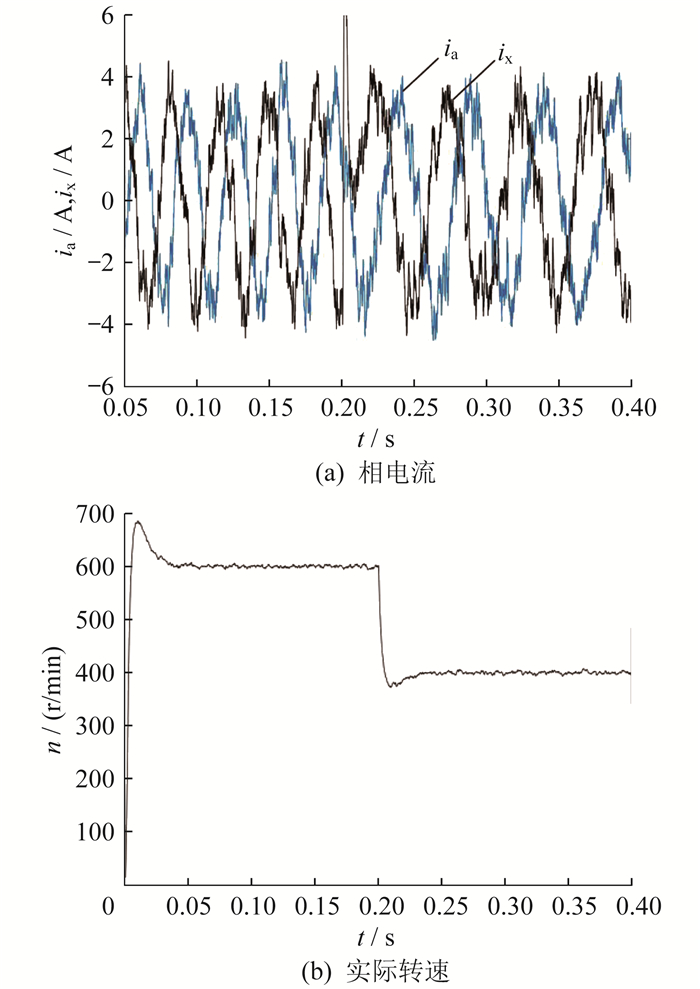
图 3为基于双dq坐标变换下的DTP-PMSM矢量控制起动-降速仿真波形。其中,ia、ix分别为第1套三相绕组a相和第2套三相绕组x相的相电流,n为实际转速。负载转矩为20 N∙m,初始给定转速n0为600 r/min,响应时间约为40 ms,第0.2 s时,给定转速由600 r/min变为400 r/min。响应时间约为47 ms。
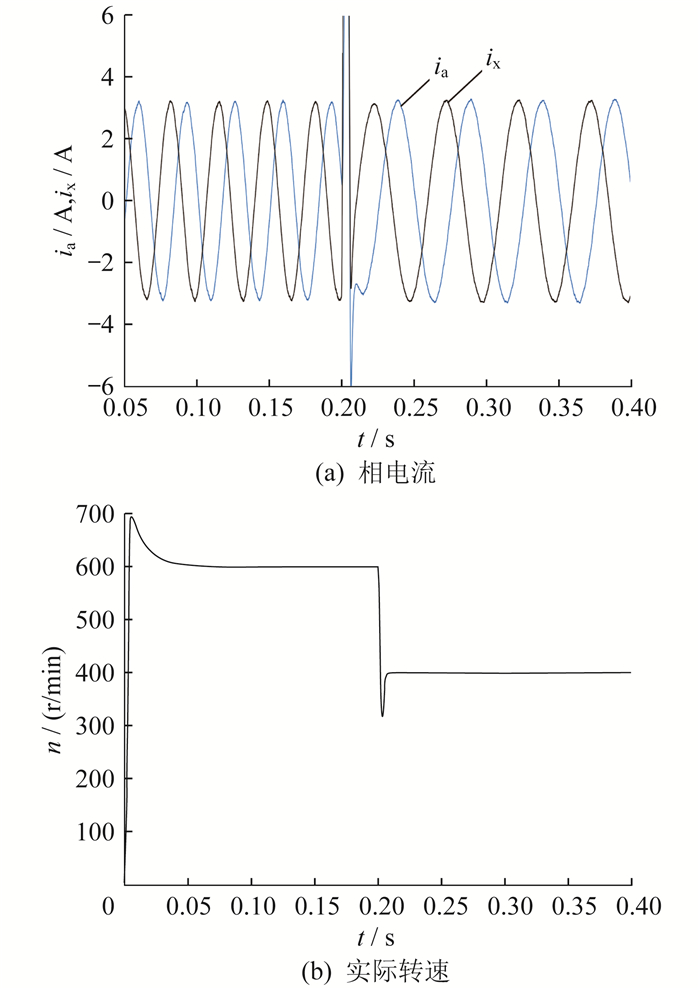
图 4为基于双dq坐标变换下的DTP-PMSM多矢量模型预测电流控制起动-降速仿真波形。负载转矩为20 N∙m,初始给定转速n0为600 r/min,响应时间约为38 ms,第0.2 s时,给定转速由600 r/min变为400 r/min。响应时间约为12 ms。
对比图 3和图 4可知,两种控制方法得到的相电流都为正弦波形,但前者相电流波形抖动较大,有较为明显的毛刺,而后者波形更为平滑,波动更小。初步证明多矢量模型预测电流控制在快速起动-降速时对DTP-PMSM的电流有较好的控制效果。
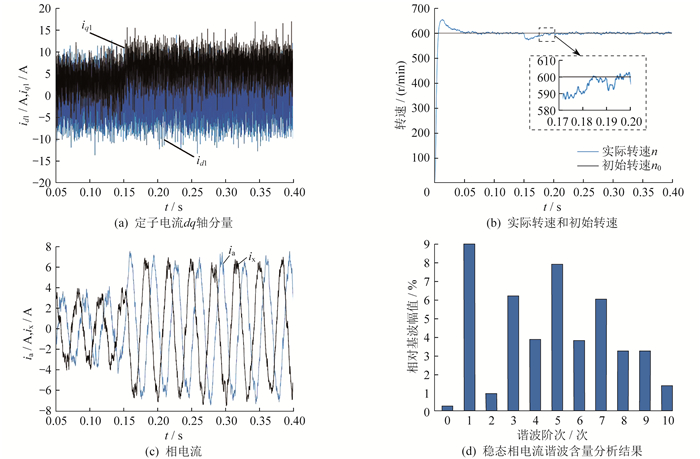
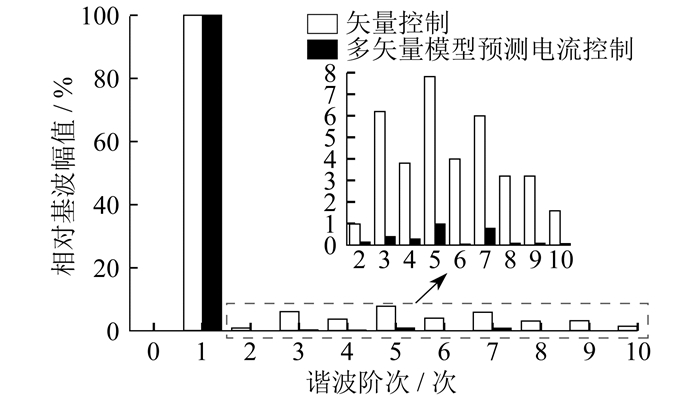
为了验证负载突变情况下的效果,初始给定转速n0为600 r/min,负载转矩在0.15 s时由20 N∙m突增至40 N∙m,对突然加负载情况下的定子电流dq轴分量以及稳定后的相电流波形进行相关数据分析,得到的DTP-PMSM矢量控制和多矢量模型预测电流控制系统仿真运行结果分别如图 5和图 6所示。图 7为两种控制策略下稳态相电流谐波含量分析结果对比。
通过对图 5(d)的详细分析可知:电流的基波频率为30 Hz,其对应的基波幅值为6.337,谐波阶次为1,并且相对基波幅值设定为100%(注意图中纵坐标并未完全展示);除基波外,显著存在的谐波分量主要集中在3次、5次和7次谐波上,3次谐波的相对基波幅值约为6.2%,5次谐波的相对基波幅值约为8.0%,而7次谐波的相对基波幅值则约为6.0%。同样,在图 6(d)中:电流的基波频率为30 Hz,其对应的基波幅值为6.52,谐波阶次仍为1,并且基波幅值也为100%(图中未完全展示纵坐标);谐波分量构成与图 5(d)类似,但各次谐波的相对基波幅值显著降低,其中3次谐波的相对基波幅值约为0.4%,5次谐波的相对基波幅值约为1.0%,而7次谐波的相对基波幅值约为0.8%。
对比上述仿真结果,可得出以下结论:当DTP-PMSM采用本文提出的多矢量模型预测电流控制策略时,在电机起动、降速以及负载突变等动态过程中,均展现出快速且准确的稳态响应。相比于传统的矢量控制方法,多矢量模型预测电流控制策略在双dq坐标变换下显著减少了电流在dq轴分量上的脉动。这得益于控制过程中期望电压矢量的合成可以覆盖任何方向和大小,同时结合双dq轴电流无差拍控制计算电压作用时间,实现了对双dq轴电流的无差拍控制,从而有效减少了电流脉动。在转速性能方面,尽管电机在带载起动时存在一定的超调现象,且超调量可能超过传统矢量控制,但在转速或负载突变的情况下,采用多矢量模型预测电流控制的电机展现出更强的稳定性,能够更快达到稳态并维持更小的波动。进一步分析DTP-PMSM的运行特性可知,由于该电机具有高阶、非线性和强耦合特性,其运行过程中易产生高次谐波。通过对比图 7中稳态相电流谐波含量分析结果可知:采用传统矢量控制时,相电流的畸变较为严重,总谐波失真(Total Harmonic Distortion,THD)为48.30%;而基于多矢量模型预测电流控制策略下的稳定相电流,其THD为7.86%,比采用传统矢量控制时减少了40.44%,显著改善了电流质量。
4 结论
针对DTP-PMSM的电流脉动问题,本文提出了一种多矢量模型预测电流控制策略。该方法通过有效电压矢量和零矢量的等效合成,生成可灵活调节方向和幅值的目标电压矢量。通过6次电流预测即能选出最优电压矢量,有效改善电机控制性能。仿真结果表明:
(1) 在恒定转速以及突加负载条件下,本文采用无差拍控制策略,实现了d轴和q轴电流的无差拍控制,显著减小dq轴电流脉动,提升了系统稳态性能与控制精度;
(2) 该方法通过控制逆变器开关状态即可实现目标,且相比于传统PWM矢量控制方法,该方法可以减少逆变器在宽频范围内谐波的产生,进而有效降低电流谐波含量。
参考文献
-
[1]DEMIR Y, AYDIN M. A novel dual three-phase permanent magnet synchronous motor with asymmetric stator winding[J]. IEEE Transactions on Magnetics, 2016, 52(7): 8105005.
-
[2]徐艳平, 张保程, 周钦. 永磁同步电机双矢量模型预测电流控制[J]. 电工技术学报, 2017, 32(20): 222-230.
-
[3]周长攀, 苏健勇, 杨贵杰. 双三相永磁同步电机全调制比范围空间矢量脉宽调制[J]. 电工技术学报, 2015, 30(10): 90-100.
-
[4]黄林森, 赵文祥, 吉敬华, 等. 稳态性能改善的双三相永磁电机直接转矩控制[J]. 电工技术学报, 2022, 37(2): 355-367.
-
[5]AHMAD M, WANG Z, YAN S, et al. Comparative analysis of two and four current loops for vector controlled dualthree phase permanent magnet synchronous motor[J]. Electronics, 2018, 7(11): 269. DOI:10.3390/electronics7110269
-
[6]SON D K, KWON S H, KIM D O, et al. Control comparison for the coordinate transformation of an asymmetric dual three phase synchronous motor in healthy and single-phase open fault states[J]. Energies, 2021, 14(6): 1735. DOI:10.3390/en14061735
-
[7]ZHANG Q, PAN H L, WANG Z H, et al. Torque increase strategy of dual three-phase permanent magnet synchronous motor based on VSD model harmonic current injection[C]// 2022 25th International Conference on Electrical Machines and Systems(ICEMS). Chiang Mai, Thailand: IEEE, 2022: 1-6.
-
[8]RUBINO S, DORDEVIC O, BOJOI R, et al. Modular vector control of multi-three-phase permanent magnet synchronous motors[J]. IEEE Transactions on Industrial Electronics, 2021, 68(10): 9136-9147. DOI:10.1109/TIE.2020.3026271
-
[9]张建亚, 王凯, 朱姝姝, 等. 双三相永磁同步电机多谐波电流协同控制策略[J]. 中国电机工程学报, 2020, 40(2): 644-651.
-
[10]耿强, 王亮, 周湛清, 等. 五桥臂逆变器双永磁电机三矢量预测控制[J]. 电工技术学报, 2021, 36(1): 87-95.
-
[11]冯凌, 付建国, 廖丽诚, 等. 一种改进的永磁同步牵引电机低开关频率模型预测直接转矩控制策略[J]. 中国电机工程学报, 2021, 41(21): 7507-7516.
-
[12]BARRERO F, ARAHAL M R, GREGOR R, et al. A proof of concept study of predictive current control for VSI-driven asymmetrical dual three-phase AC machines[J]. IEEE Transactions on Industrial Electronics, 2009, 6(6): 1937-1954.
-
[13]REN H, SONG W, YANG Y. Deadbeat model predictive control for dual three-phase pmsm drives[C]//2021 IEEE International Conference on Predictive Control of Electrical Drives and Power Electronics(PRECEDE). Jinan, China: IEEE, 2021: 213-217.
-
[14]SUN C, SUN D, ZHENG Z, et al. Simplified model predictive control for dual inverter-fed open-winding permanent magnet synchronous motor[J]. IEEE Transactions on Energy Conversion, 2018, 33(4): 1846-1854. DOI:10.1109/TEC.2018.2841012
-
[15]孙全增, 张志锋. 双三相永磁同步电机低共模电压模型预测电流控制[J]. 电工技术学报, 2023, 38(14): 3708-3722.
-
[16]LUO Y, LIU C. Multi-vector-based model predictive torque control for a six-phase pmsm motor with fixed switching frequency[J]. IEEE Transactions on Energy Conversion, 2019, 34(3): 1369-1379. DOI:10.1109/TEC.2019.2917616
-
[17]杨金波, 杨贵杰, 李铁才. 双三相永磁同步电机的建模与矢量控制[J]. 电机与控制学报, 2010, 14(6): 1-7.
-
[18]牛里, 杨明, 刘可述, 等. 永磁同步电机电流预测控制算法[J]. 中国电机工程学报, 2012, 32(6): 131-137.
-
[19]GRANDI G, SERRA G, TANI A. Space vector modulation of a six-phase VSI based on three-phase decomposition[C]// 2008 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM). Ischia, Italy: IEEE, 2008: 674-679.