在“双碳”战略目标下，海上风电产业已成为主要沿海国家和地区减少碳排放、培育新兴产业的重要方向。变频电机作为海上风电机组的关键部件，其安全性和可靠性至关重要。变频电机的故障包括定子绕组绝缘故障、轴承故障、气隙偏心等。其中，轴承故障最为普遍，约占总故障的40%^[1]。因此，研究变频电机轴承故障诊断和监测技术，实现精确运维和早期故障预警，具有重要的理论意义和应用价值^[2]。

目前，国内外针对变频电机轴承故障诊断技术开展了大量的研究，主要研究方法包括基于振动信号的振动分析法和基于定子电流信号的定子电流分析法。从传感器收集的振动信号包括大量与故障相关的信息，振动分析法通过分析不同状态下振动信号的规律性进行故障诊断^[3]。文献[4]利用振动信号与改进的小波变换相结合，进行轴承故障的早期诊断。文献[5]提出了一种基于集合经验模态分解的多尺度独立元素分析方法，用于旋转轴承的故障诊断。振动信号易于获得，但测量需要额外的振动传感器，且信号易受到安装位置和环境噪声的影响^[6]。定子电流分析法通过监测机器定子电流的变化来识别轴承故障。文献[7]提出了一种利用定子电流信号频率特征进行线性判别分析的分类方法，实现电机轴承故障的有效诊断。文献[8]使用小波分析对电机相电流进行分解，利用特征频率处的谐波能量来进行轴承故障诊断。定子电流法无需额外的传感器，但是定子电流信号中所包含的故障信号分量微弱，并且可能会受到类似基频电流等干扰，从而使得提取特征的难度加大。

针对传统变频电机轴承故障诊断方法易受到低频噪声和基频电流干扰的问题，本文提出了一种利用脉冲宽度调制(Pulse Width Modulation，PWM)开关高频振荡进行变频电机轴承故障诊断的新方法。首先，分析了变频电机轴承故障诊断的机理以及轴承电流的产生机理和流通路径，并用仿真验证了PWM开关dv/dt轴承电流随轴承油膜电容的减小而减小的特性，因此dv/dt轴承电流可作为故障状态敏感特征量；然后，利用dv/dt轴承电流不易测量且流入地面的dv/dt轴承电流是地线电流的一部分这一特点，将地线电流中的高频振荡信号作为故障诊断特征变量和数据源；最后，设计了一种用于电机轴承故障诊断的轻量级一维卷积神经网络(One-Dimensional Convolutional Neural Network，1DCNN)模型进行特征提取和故障分类。

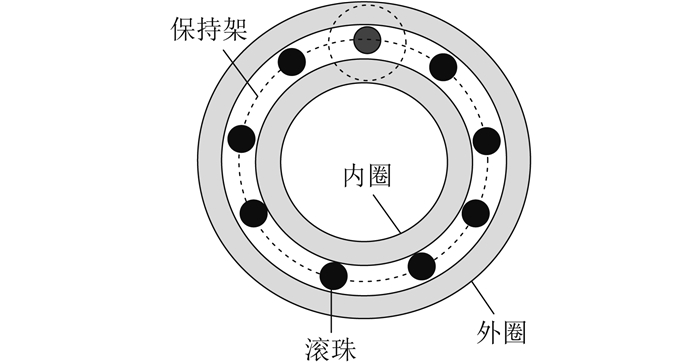
变频电机系统中，轴承结构如图 1所示。

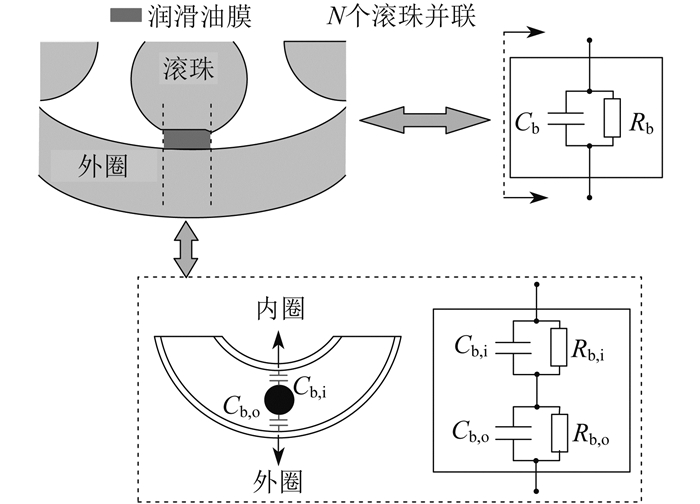
其中，润滑油脂能将轴承滚珠与内外圈分离，在电机稳定运行时形成一层绝缘润滑油膜。从电路角度来看，润滑油膜的绝缘性能使滚珠和滚道之间形成一个电容器^[9]。轴承油膜电容如图 2所示。

其中，C_b和R_b分别为轴承整体油膜电容和油膜电阻，R_b，i和R_b，o分别为轴承内外滚道与单个滚珠之间等效的油膜电阻，C_b，i和C_b，o分别为轴承内外滚道与单个滚珠之间形成的等效电容。对于整个轴承来说，每个滚珠和内外圈之间电容并联，轴承整体油膜电容C_b的计算公式为

$ \begin{equation*} C_{\mathrm{b}}=\frac{C_{\mathrm{b}, \mathrm{i}} C_{\mathrm{b}, \mathrm{o}}}{C_{\mathrm{b}, \mathrm{i}}+C_{\mathrm{b}, \mathrm{o}}} \end{equation*} $

(1)

PWM变频调速技术被广泛应用于电机拖动系统，具有转矩脉动小、节能、效率高等优点，但同时也存在许多负面效应。在逆变器供电的电机系统中将产生高dv/dt(电压变化率)的非零高频PWM共模电压，在逆变器共模电压的作用下，经过电机内部电容的耦合，在电机轴承上产生了轴承电压，当轴承电压大于轴承润滑脂绝缘电压临界值时，轴承将产生破坏性的轴承电流，轴承电流会对轴承产生电腐蚀，并导致凹槽损伤^[10]。轴承油膜电容被击穿后，轴承与导轨之间的接触部分相当于一个电阻，失去了润滑油膜的隔离和保护。因此，轴承失效后轴承油膜电容变小，不同类型的机械故障使轴承油膜电容发生变化。

将轴承油膜电容C_b看作由许多因素决定的线性阻抗，可表示为

$ \begin{equation*} C_{\mathrm{b}}=C\left(Q, V, T, \eta, \lambda, \varLambda, \varepsilon_{\mathrm{r}}\right) \end{equation*} $

(2)

式中：C(·)——线性阻抗函数；

Q——轴承机械载荷；

V——润滑脂流动速度；

T——润滑脂温度；

η——润滑脂黏度系数；

λ——润滑添加剂影响因素；

Λ——润滑油膜厚度；

ε_r——润滑脂相对介电常数。

对于变频电机系统而言，不同类型的轴承故障导致轴承油膜电容不同程度地减小，轴承油膜电容C_b属于电机寄生电容的一部分，而寄生电容则影响着变频电机系统中的高频振荡波形。

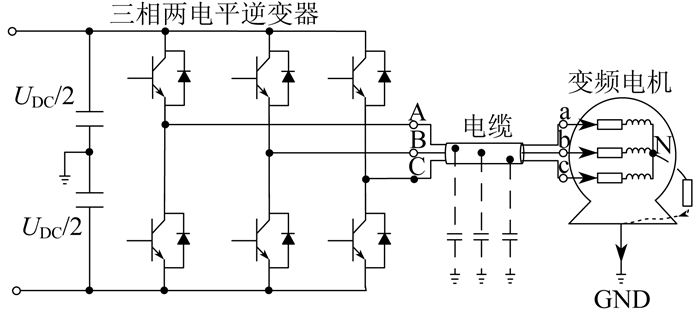
在可调速驱动系统中，电机的转速由PWM逆变器控制，功率器件快速开关为变频电机提供宽带激励电压。三相两电平逆变器驱动变频电机系统如图 3所示。其中，A、B、C和a、b、c分别表示逆变器和变频电机的三相，N表示中性线，GND表示接地端。在PWM运行期间，每相存在两种电平状态，即输出相电压取正直流母线电压(+U_DC/2)或负直流母线电压(−U_DC/2)。

具有高dv/dt的PWM共模电压U_com是轴承电流的激励源，而电机内部的寄生电容将为轴承电流提供共模耦合路径。根据产生机理的不同，轴承电流可分为dv/dt轴承电流、EDM(Electric Discharge Machining)轴承电流、高频循环轴承电流和转轴接地型轴承电流4种。本文主要研究dv/dt轴承电流。dv/dt轴承电流可看作容性轴承电流，主要由具有高dv/dt的PWM共模电压产生。当电机正常运行时，轴承滚珠和内外圈之间会形成一层相对稳定的润滑油膜，相当于一个电容器，在高频共模电压的作用下，将产生流过轴承油膜电容的充电和放电电流。dv/dt轴承电流的路径为：定子绕组—电机转子—轴承—电机机架接地。

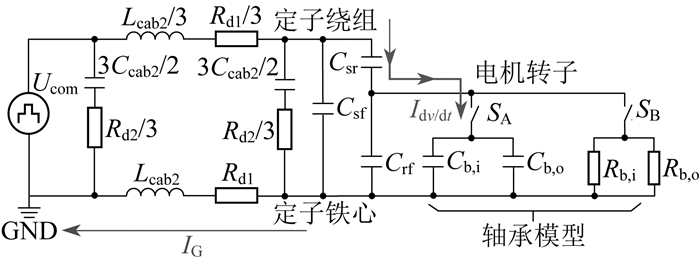
为了进一步研究dv/dt轴承电流与轴承油膜电容之间的关系，需要建立共模等效电路模型对电机内部的寄生电容进行分析。变频电机系统高频共模等效电路如图 4所示。

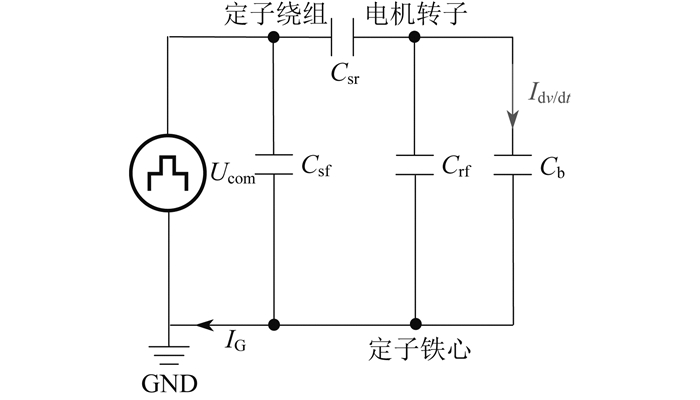
图 4中，U_com为共模电压，C_cab2为电缆的绝缘电容，L_cab2为电缆的回路电感，R_d1为电缆的回路电阻，R_d2为电缆的绝缘电阻，C_sf为定子绕组与定子铁心之间的寄生电容，C_sr为定子绕组和电机转子之间的寄生电容，C_rf为定子铁心与电机转子之间的寄生电容，I_dv/dt为dv/dt轴承电流，I_G为地线电流，开关S_A和S_B用于模拟轴承状态，电机低速运转时闭合S_A，电机正常运转时闭合S_B。由图 4可知，dv/dt轴承电流从定子绕组流向电机转子，通过定子绕组与电机转子之间的寄生电容C_sr，然后通过轴承油膜电容C_b流向地面。为了便于分析，本文忽略一些影响较小的寄生电容，简化的变频电机系统高频共模等效电路如图 5所示。

根据电机寄生电容的分压效应，共模电压U_com在轴承上产生轴承电压U_b，U_b和U_com的比值为轴承电压分压比r_Bv^[11]，dv/dt轴承电流I_dv/dt的计算公式如下：

$r_{\mathrm{Bv}}=\frac{U_{\mathrm{b}}}{U_{\mathrm{com}}}=\frac{C_{\mathrm{sr}}}{C_{\mathrm{sr}}+C_{\mathrm{rf}}+C_{\mathrm{b}}} $

(3)

$ I_{\mathrm{dv} /\mathrm{d} t}=C_{\mathrm{b}} \frac{\mathrm{~d} U_{\mathrm{b}}}{\mathrm{~d} t}=\frac{C_{\mathrm{sr}}}{\frac{C_{\mathrm{sr}}}{C_{\mathrm{b}}}+\frac{C_{\mathrm{rf}}}{C_{\mathrm{b}}}+1} \cdot \frac{\mathrm{~d} U_{\mathrm{com}}}{\mathrm{~d} t} $

(4)

通过分析式(4)可以发现，假设电机其他寄生参数不发生改变，在变频器dv/dt恒定的情况下，dU_com/dt为常数，dv/dt轴承电流随着轴承油膜电容的减小而减小。然而，直接测量轴承电流往往需要复杂的机械调整和绝缘层，测量过程十分复杂。相对而言，地线电流可以通过非侵入的方式进行测量。dv/dt轴承电流作为地线电流的一部分，因此有望利用地线电流进行轴承故障诊断。

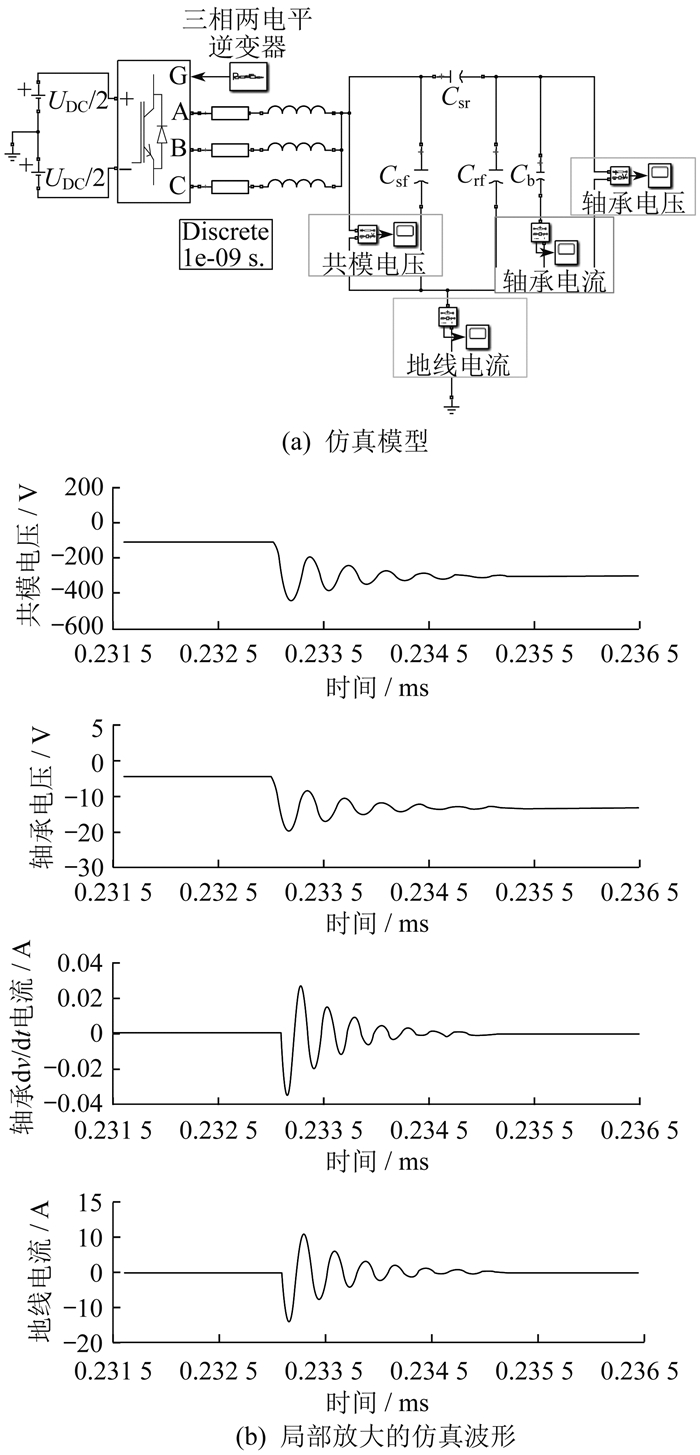
本文通过建模和仿真，研究了轴承故障对高频dv/dt轴承电流的影响。根据图 5，利用MATLAB/Simulink建立了电机高频dv/dt轴承电流仿真模型，仿真模型和仿真结果如图 6所示。电机参数如表 1所示。

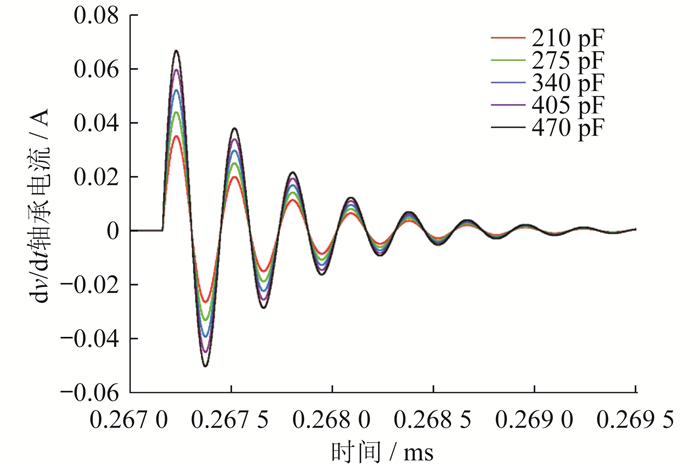
图 7为不同轴承油膜电容下模拟的dv/dt轴承电流，轴承油膜电容变化范围为210~470 pF，可反应不同类型的轴承故障状态。

由图 7可知，dv/dt轴承电流的幅值大小随着轴承油膜电容的减小而减小，因此dv/dt轴承电流可作为故障状态敏感特征量。由图 6(b)可知，dv/dt轴承电流作为地线电流的一个分量，其变化范围相比地线电流较小，在地线电流中占比较小，因此将地线电流作为故障诊断特征变量，但直接从地线电流信号提取轴承故障特征面临挑战。鉴于深度学习方法从原始数据中挖掘潜在特征方面的潜力，本文采用1DCNN模型对轴承故障进行特征提取和故障分类。

本文所提出的基于PWM开关高频振荡的变频电机轴承故障诊断方法具体步骤如下。

步骤1    将高频电流传感器安装在接地线上，测量不同类型轴承故障状态下地线电流。

步骤2    对高频振荡的地线电流进行截取和数据预处理，作为样本数据集，并按照7∶3的比例划分训练集和测试集。

步骤3    建立一种轻量级的1DCNN模型进行模型训练和测试，将地线电流样本数据集作为输入信号，并输出故障诊断结果。

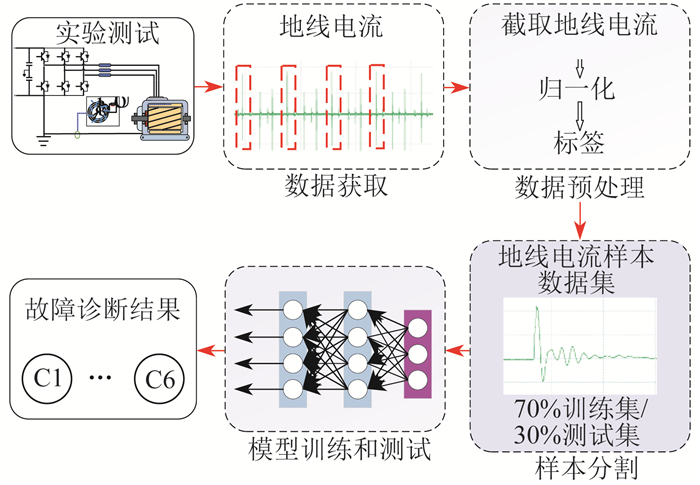
故障诊断框架如图 8所示。其中，C1，C2，C3，…，C6为故障类型编号。

1DCNN是一种前馈神经网络，具有很强的特征学习和特征提取能力。1DCNN的基本结构一般由输入层、卷积层、池化层、全连接层和输出层组成，其结构参数如表 2所示。

卷积层对输入数据进行卷积操作，可以将多维特征映射到一个新的空间中，从而增强特征的线性可分性。卷积过程公式为

$ \begin{equation*} \boldsymbol{X}_{j}^{l}=f\left[\sum\limits_{i \in M}\left(\boldsymbol{X}_{i}^{l-1} \boldsymbol{w}_{i j}^{l}\right)+\boldsymbol{b}_{j}^{l}\right] \end{equation*} $

(5)

式中：$\boldsymbol{X}_{j}^{\prime}$——第l层的第j个输出；

f (·)——激活函数；

M——连接到第l层的特征图数量；

$\boldsymbol w_{i j}^{l}$——连接第l层的第j个映射和第l - 1层的第i个映射的卷积核；

$\boldsymbol{b}_{j}^{\prime}$ —第l层的第j个输出偏差。

在卷积层之后，将池化层应用于前1层的每个特征映射。在池化层中，通过输出相邻场中特征的统计量，对每个图中的特征进行下采样。其公式为

$ \begin{equation*} \boldsymbol{X}_{j}^{l+1}=\operatorname{pooling}\left(\boldsymbol{X}_{j}^{l}\right) \end{equation*} $

(6)

式中：pooling(·)——池化运算函数。

为了更好地保存特征，本文采用了最大池化方法。此外，采用交叉熵损失函数和Adma算法，以提高模型的更新速度。

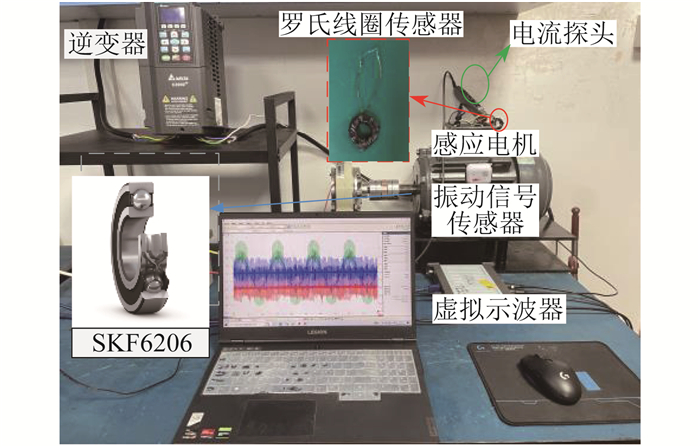
为了验证本文所提方法的可行性和有效性，搭建的变频电机实验系统如图 9所示。被测电机为380 V/3 kW 4极鼠笼式感应电机(TECO AEEV1H00L2-4)，电机轴承型号为SKF6206。逆变器型号为Delta CH2000，开关频率为4 kHz。采用高速数字示波器(Pico 5444D，采样频率为125 MHz)和上位机进行信号采集和处理。地线电流采用罗氏线圈传感器进行测量，罗氏线圈传感器测量到的是电压信号，经过相应转换得到地线电流。利用电火花加工技术模拟轴承内外圈不同尺寸的凹槽故障以及滚珠损伤。采集了3种不同的基波频率(30、40、50 Hz)下的数据，将轴承故障分为6种类型。不同类型轴承故障如表 3所示。

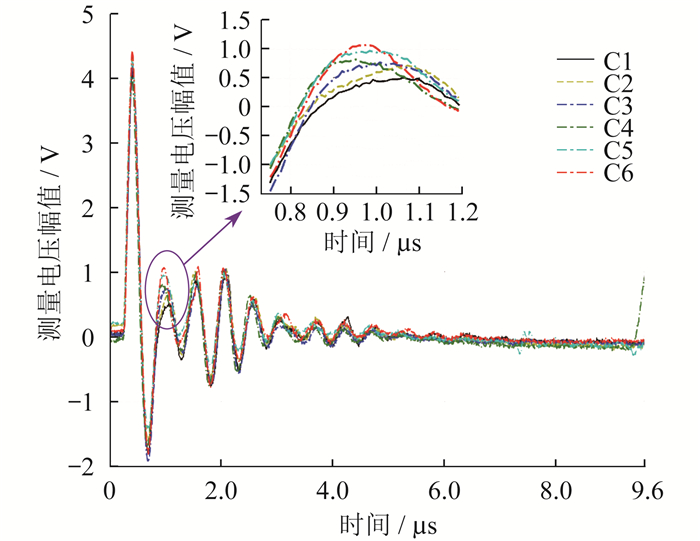
通过非侵入式高频电流传感器采集地线电流，将采集到的地线电流信号切成片段作为样本。每个样本的长度为9.6 μs，采样频率为125 MHz，共1 200个采样点。在每个指定工况下，每个故障对应400个样本，轴承故障有6种类型，因此有2 400个样本。在50 Hz的基频(即1 445 r/min的额定转速)时，测量到的不同类型轴承故障地线电流对应的测量电压波形如图 10所示。实验测得的波形与理论分析结果相一致，不同类型轴承故障状态导致地线电流发生变化，随着故障程度的加深，轴承油膜电容变小，地线电流高频振荡幅值变小。

实验采用10倍交叉验证方法。数据集分为两部分，70% 的样本(1 680个样本)用于训练，30%的样本(720个样本)用于测试。使用本文所提方法，在50 Hz工况下的轴承故障诊断结果如图 11~图 14所示。

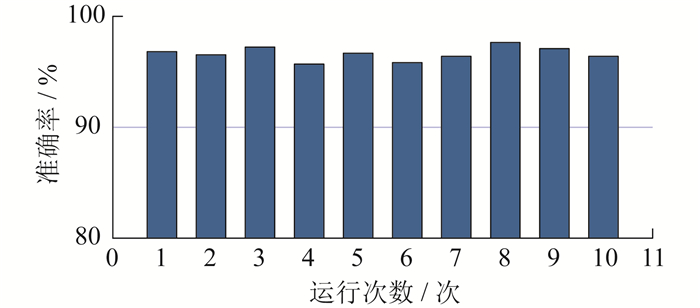
图 11结果表明，该方法在10次运算中的准确率均在95% 以上，最高和最低分别为97.64% 和95.69%，10次运算的平均准确率为96.63%，证明了该方法的稳定性。

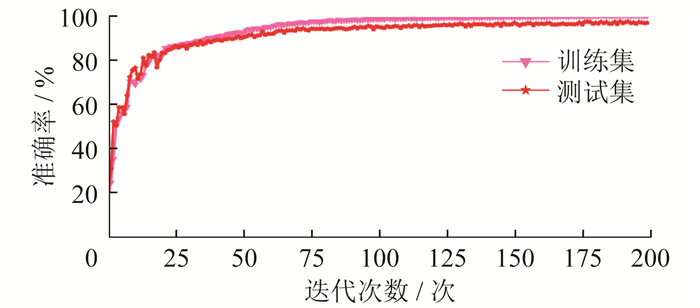
图 12显示了1DCNN模型随着迭代次数增加时的准确率曲线，其结果表明，在迭代75次后，测试结果达到稳定。

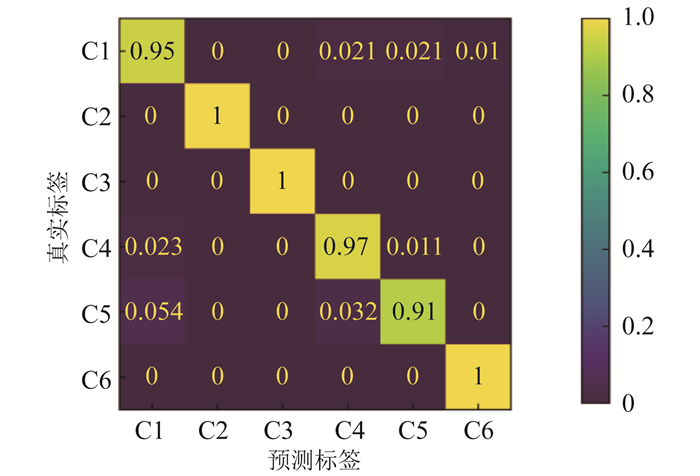
图 13显示了第1次运行的混淆矩阵，混淆矩阵的对角线元素表示不同类型的轴承故障状态的故障诊断精度。其结果表明该方法在不同类型轴承故障状态下准确率均在90% 以上。此外，利用随机邻域嵌入(t-Distributed Stochastic Neighbor Embedding，t-SNE)将分类结果可视化。

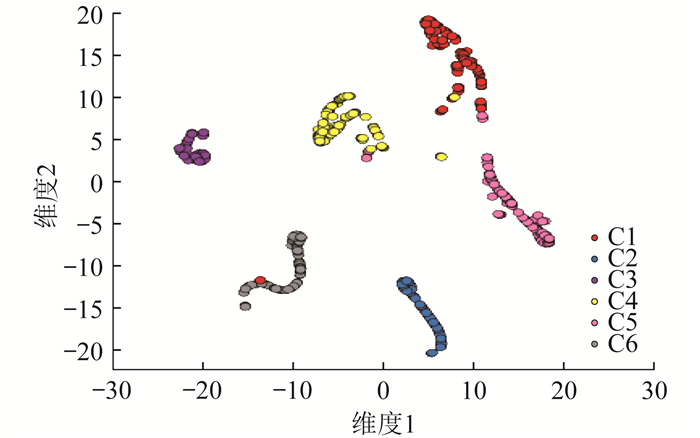
图 14显示了1DCNN模型输出层的t-SNE降维图，其中不同颜色代表不同类型轴承故障，其结果表明本文采用的1DCNN模型能够成功将PWM开关地线电流波形进行分类，表现出优异的诊断性能。

为了解决传统变频电机轴承故障诊断方法易受到低频噪声和基频电流干扰的问题，本文提出了一种利用变频器PWM开关高频振荡进行变频电机轴承故障诊断的新方法，为变频电机轴承故障诊断提供了一条新思路。PWM开关高频振荡频率为MHz级，其信号与低频噪声耦合程度低，且利用了谐振效应，体现出较高的灵敏度。实验证明本文所提方法在单一工况下平均准确率达到96.63%，能够准确诊断变频电机轴承故障。