|
|
|
发布时间: 2024-12-28 |
智能电网技术 |
|
|
|
收稿日期: 2023-12-27
中图法分类号: TM73
文献标识码: A
文章编号: 2096-8299(2024)06-0579-08
|
摘要
在新型电力系统建设和整县光伏开发的背景下,海量分布式光伏(DPV)的接入给配电网安全高效运行带来巨大威胁,亟需评估配电网DPV承载能力,以量化高比例分布式光伏对配电网带来的综合影响。首先,构建了多场景下的源荷不确定性模型;其次,建立了DPV承载能力评估模型求解配电网可接入的DPV最大容量;最后,提出了考虑多因素影响的DPV承载能力评估体系,以反映配电网的运行水平,并通过电网实例验证了所提方法的科学性。
关键词
配电网; 分布式光伏; 承载能力; 源荷不确定性
Abstract
In the context of the construction of new power systems and the development of photovoltaic systems throughout the county, the integration of massive distributed photovoltaics (DPV) poses a huge threat to the safe and efficient operation of the distribution network. It is urgent to evaluate the capacity of DPV in the distribution network to quantify the comprehensive impact of high proportion DPV on the distribution network. Firstly, a source load uncertainty model in multiple scenarios is constructed. Secondly, a DPV carrying capacity assessment model is established to determine the maximum capacity of DPV that can be connected to the distribution network. Finally, a DPV capacity evaluation system considering multiple factors is proposed to reflect the operational level of the distribution network, and the scientificity of the proposed method is verified through power grid cases.
Key words
distribution grid; distributed photovoltaic; capacity; source load uncertainty
随着“双碳”目标的提出以及国家对整县光伏开发政策的全面实施[1],以分布式光伏],以分布式光伏(Distributed Photovoltaic,DPV)为代表的分布式电源(Distributed Generation,D G)广泛接入配电系统[2]。然而大量DPV接入后将大幅改变配电网潮流分布,增加配电网电压越限的风险,并导致电压分布不均、质量下降等问题[3]。同时,DPV输出功率的随机、波动、不确定性以及柔性负荷对需求响应(Demand Response,DR)的广泛参与将导致电网运行特性发生显著变化,为配电网规划与优化调度带来全新挑战[4]。例如,源荷功率和动力]。例如,源荷功率和动力的平衡难度提高、经济效益恶化、电网运行效率降低,以及无法适应高渗透率新能源发电接入和高效使用的新需求等[5]。因此,亟需在考虑源荷运行不确定性的前提下进行配电网DPV承载能力评估研究与分析,从而指导DPV在配电网层面的合理布局与接入,为DPV大规模开发利用提供有效的理论支撑。
DPV承载能力常表示为:在电网安全稳定运行以及满足相应约束的基础上,配电网所能接入DPV的最大限度容量[6]。结合此定义,从DPV投资规划与工程实际出发,研究DPV承载能力量化评估方法将具备较高的工程实用价值和学术意义[7]。近年来,已有部分专家针对配电网DPV承载能力进行研究分析。文献[8]建立了可有效量化多重因素影响的配电网DPV承载能力评估指标,但未考虑DPV输出功率不确定性的影响。文献[9]提出了一种考虑电压约束的DG最大准入容量优化模型,但约束条件较为单一且只考虑了负荷的不确定性。文献[10]提出了一种基于机会约束的配电网DPV承载力提升方法,但并未建立量化指标对DPV接入后的配电网运行水平进行评估。上述成果虽在一定程度上推进了对DPV承载能力的研究,但未有效考虑当前配电网运行中源荷资源的不确定性,未建立精细化的模型,难以得到精准的评估结果。
针对上述问题,本文提出考虑源荷不确定性的配电网DPV承载能力评估方法。首先,综合考虑源荷双侧的不确定性,建立源荷运行场景,提取模型;然后,在此基础上,考虑多种约束条件,构建DPV承载能力评估模型;最后,提出相应评估体系,量化分析接入DPV后配电网在不同场景下的运行水平,为新型配电网运行调度与新能源规划投资提供有效的数据支撑。
1 源荷不确定性模型
对源荷预测不确定性进行建模,并通过多场景技术描述源荷运行的随机过程,其中源侧为光伏输出功率不确定性,荷侧为负荷需求不确定性。
1.1 考虑预测误差的源荷运行场景生成模型
预测误差是源荷不确定性的主要来源,可利用场景生成的方法将随机优化问题转换为确定性优化问题,同时简化了计算复杂度[11]。对光伏输出功率和常规负荷用能进行建模,将实际值表示为预测值与随机预测误差值之和,即:
| $\left\{\begin{array}{l} \tilde{P}_{\mathrm{PV}, t}=\bar{P}_{\mathrm{PV}, t}+\Delta \xi_{\mathrm{PV}, t} \\ \tilde{P}_{\mathrm{L}, t}=\bar{P}_{\mathrm{L}, t}+\Delta \xi_{\mathrm{L}, t} \end{array}\right.$ | (1) |
式中:
ΔξPV,t——t时段光伏输出功率预测误差;
ΔξL,t——t时段常规负荷预测误差。
DPV输出功率的预测误差服从TLS(T-location-scale)分布[12],而负荷的预测误差服从均值为零的正态分布[13]。
风光预测误差Δξ的TLS分布f(Δξ)可表示为
| $\begin{aligned} & f(\Delta \xi)= \\ & \frac{\Gamma\left[\left(v_t+1\right) / 2\right]}{\sigma_{\mathrm{DG}, t} \sqrt{v_t {\rm{ \mathsf{ π}}}} \Gamma\left(v_t / 2\right)}\left\{\frac{v_t+\left[\left(\Delta \xi-\mu_t\right) / \sigma_{\mathrm{DG}, t}\right]^2}{v_t}\right\}^{-\frac{v_i+1}{2}} \end{aligned}$ | (2) |
式中:Γ——伽马函数;
vt——t时段光伏TLS分布的形状参数;
σDG, t——t时段光伏TLS分布的方差参数;
μt——t时段光伏TLS分布的位置参数。
考虑预测偏差的负荷分布概率密度函数
| $F\left(\tilde{P}_{\mathrm{L}, t}\right)=\frac{1}{\sqrt{2 {\rm{ \mathsf{ π}}}} \sigma_{\mathrm{L}, t}} \mathrm{e}^{-\frac{(\tilde{P}_{\mathrm{L},t} -\bar{P}_{\mathrm{L},t })^2}{2 \sigma_{\mathrm{L}, t}^2}}$ | (3) |
式中:σL, t——t时段常规负荷的方差。
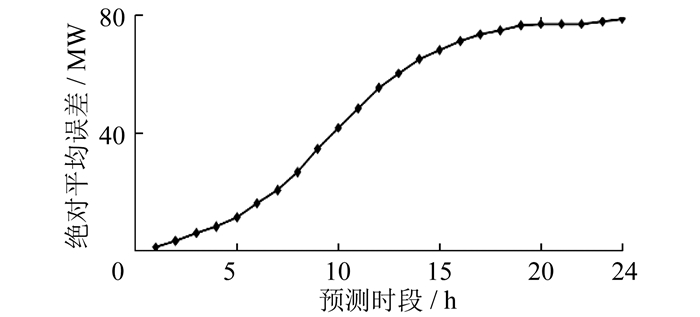
根据上述公式,基于文献[14]中的方法进行时序下的分段分布拟合。为证明采用时序分段分布拟合方法的有效性,现对DG日输出功率24 h预测误差进行统计分析,得到不同预测时段下的绝对平均误差变化趋势如图 1所示。
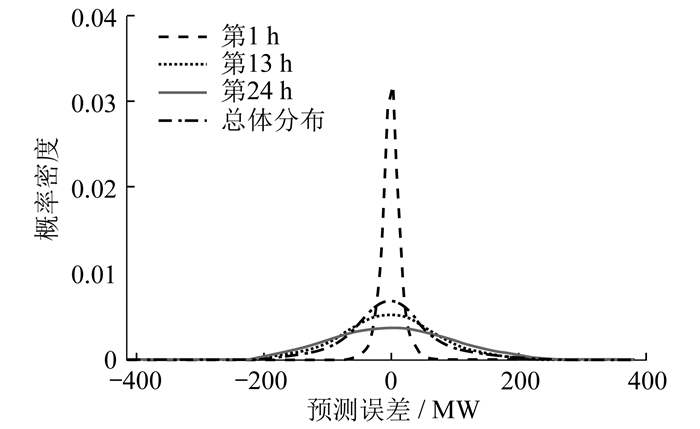
将常规全时段拟合方法的总体分布误差拟合曲线与提取的第1 h、13 h、24 h 3个时段的拟合曲线进行对比,结果如图 2所示。
由图 1可知,随着预测时段增加,误差呈现非线性增大的趋势,并在第20 h左右趋于稳定。这表明不同时段下的误差特征具有显著的差异,如果使用统一的拟合方法,将很难展示这种特征。根据图 2的预测结果可知,不同时段下的拟合曲线之间存在明显差异,时序分段拟合可以更准确地反映误差的真实分布情况。
在得到预测误差分布后,进一步利用采样方式生成确定性的光伏输出功率运行场景以刻画其随机性。本文选择拉丁超立方采样(Latin Hypercube Sampling,LHS)进行模拟。相较于蒙特卡洛模拟等方法,LHS基于分层采样的方式可保证采样点包含所有的采样区域,使结果更具代表性[15],在保证均匀分布的前提下,尽可能地减少采样点数目,以提高计算效率。LHS随机变量的采样值为
| $X_{\mathrm{m}}^h=F_{\mathrm{m}}^{-1}\left(U^h\right)=F_{\mathrm{m}}^{-1}[(U+h-1) / H]$ | (4) |
式中:Xmh——随机变量Xm的第h次采样值;
Fm——分布函数;
Uh——将[0, 1]区间H等分后第h个子区间随机数,Uh=(U+h−1)/H,U∈[0, 1]。
1.2 源荷运行场景削减方法
通过LHS生成的原始场景数量巨大且计算繁杂,故需要对其进法对目标场景数的依赖,以及聚类初值需凭借经验指定具有较大主观性等缺陷,本文提出了一种改进层次K-means聚类算法。一方面,利用最大距离法得到聚类初值,通过建立客观的场景距离模型计算得到聚类初值K,避免了取值的主观性;另一方面,利用层次K-means聚类算法不依赖初始聚类中心,可根据数据内在结构自动决定最佳聚类中心数的优势,对源荷运行场景进行削减聚类,从而得到更具代表性的源荷运行场景。现以负荷为例进行说明,具体步骤如下。
步骤1 设共有M d(天)的负荷有效运行数据,负荷运行的原始场景集为P=[P1,P2,P3,…,PM],第a个场景负荷数据向量为Pa=[pa,1,pa,2,pa,3,…,pa,T],T为划分总时段数,初始聚类数为K1。
步骤2 通过最大距离法选取K1个初始聚类中心。
首先,将原始场景集中距离最大的2个场景作为初始聚类中心,两者的距离d为
| $d=\sqrt{\sum\limits_{t=1}^T\left(p_{m, t}-p_{n, t}\right)^2}$ | (5) |
式中:pm,t,pn,t——距离最大的2个场景负荷数据向量Pm、Pn的分量。
其次,在剩余的M−2个运行场景中,选择到2个初始聚类中心距离乘积最大的场景为第3个聚类中心,以此类推直到选出K1个聚类中心。
步骤3 实现K-means聚类,即所有场景归属于距离最近的聚类中心,设迭代次数λ=1,求取第λ次聚类测度函数值J(λ)。其计算公式为
| $J^{(\lambda)}=\sqrt{\frac{\sum\limits_{s=1}^{K_1} \sum\limits_{b=1}^{M_s}\left(\boldsymbol{P}_s^b-\boldsymbol{C}_s\right)^2}{M-1}}$ | (6) |
式中:Ms——第s个类别的场景数;
Psb——第s个类别中第b个场景负荷数据向量;
Cs——第s类的聚类中心。
步骤4 进行下一层次聚类。
首先,选择全部聚类中半径最大的类,类半径rs为
| $r_s=\max \left\|\boldsymbol{P}_b-\boldsymbol{C}_s\right\|, \ \ b=1, 2, 3, \cdots, M_s$ | (7) |
式中:Pb——第b个场景负荷数据向量。
其次,在该类中选择距离最大的2个场景作为新的聚类中心。
最后,利用聚类中心再次聚类,并令λ=λ+1,得到第λ+1次的J(λ+1)值。
步骤5 定义δ =[J(λ)-J(λ+1)]/J(λ)。当δ > δ0时,返回步骤4,其中δ0是给定阈值,可依据聚类测度函数变化曲线设定;反之,输出聚类结果。
步骤6 得到削减后的负荷运行典型场景的出现概率与聚类中心。
2 配电网DPV承载能力评估模型
2.1 目标函数
本文提出考虑源荷不确定性的配电网DPV承载能力评估方法,其根本目的在于有效评估DPV接入配电网的最大容量。此目标函数的具体表达式为
| $\max C=\max \left(\sum\limits_{i=1}^{N_{\mathrm{PV}}} S_i^{\mathrm{PV}}\right)$ | (8) |
式中:C——DPV可接入容量;
NPV——光伏可接入节点数;
SiPV——节点i接入的DPV容量。
2.2 约束条件
模型在考虑配电网潮流平衡约束条件、支路电流约束条件以及电压偏差约束条件等常规网络约束条件外,进一步考虑DR以及储能的调节作用,提出了DR约束条件、储能运行约束条件以及DPV运行约束条件。
为简化研究流程以及保证模型建立的可行性,本文在建模时忽略了配电网线路传输损耗,采用线性化的DistFlow模型[16]表征配电网潮流。配电网潮流方程约束条件为
| $P_{i, t}^{\mathrm{inj}}=P_{i, t}^{\mathrm{PV}}+P_{i, t}^{\mathrm{dis}}-P_{i, t}^{\mathrm{ch}}-P_{i, t}^{\mathrm{L}} $ | (9) |
| $Q_{i, t}^{\mathrm{inj}}=Q_{i, t}^{\mathrm{PV}}-Q_{i, t}^{\mathrm{L}}$ | (10) |
| $\sum\limits_{k \in \rho(i)}\left(P_{k i, t}-R_{k i} I_{k i, t}^2\right)+P_{i, t}^{\mathrm{inj}}-\sum\limits_{j \in k(i)} P_{i j, t}=0 $ | (11) |
| $\sum\limits_{k \in \rho(i)}\left(Q_{k i, t}-X_{k i} I_{k i, t}^2\right)+Q_{i, t}^{\mathrm{inj}}-\sum\limits_{j \in k(i)} Q_{i j, t}=0$ | (12) |
| $\left(U_{i, t}^2-U_{j, t}^2\right)-2\left(R_{i j} P_{i j, t}+X_{i j} Q_{i j, t}\right)+\left(R_{i j}^2+X_{i j}^2\right)I_{i j, t}^2=0$ | (13) |
| $I_{i j, t}^2 U_{i, t}^2-P_{i j, t}^2-Q_{i j, t}^2=0$ | (14) |
式中:
ρ(i)——节点i的父节点集合;
Rki,Xki——支路ki的电阻、电抗;
k(i)——节点i的子节点集合;
支路电流约束条件为
| $\left|I_{i j, t}\right| \leqslant \alpha_{i j, t} I_{i j, \max }$ | (15) |
式中:
电压偏差约束条件为
| $\left(1-\varepsilon_{\text {low }}\right) U_{\mathrm{N}} \leqslant U_{i, t} \leqslant\left(1+\varepsilon_{\text {up }}\right) U_{\mathrm{N}}$ | (16) |
式中:εlow,εup——节点电压偏差的下限和上限;
UN——标准电压。
DR约束条件为
| $-\xi_{i, t}=\frac{\Delta P_{i, t}}{\Delta \rho_{i, t}}=\frac{P_{i, t}^{\text {cur }}-P_{i, t}}{\rho_{i, t}^{\text {cur }}-\rho_{i, t}} $ | (17) |
| $\rho_{i, t}^{\text {cur }}=\left\{\begin{array}{l} \rho^{\text {peak }}, t \in T^{\text {peak }} \\ \rho^{\text {valley }}, t \in T^{\text {valley }} \end{array}\right.$ | (18) |
| $\sum\limits_{i=1}^N \sum\limits_{t=1}^T P_{i, t}^{\text {cur }}=\sum\limits_{i=1}^N \sum\limits_{t=1}^T P_{i, t} $ | (19) |
| $\rho_{i, t}^{\text {cur,} \min } \leqslant \rho_{i, t}^{\text {cur }} \leqslant \rho_{i, t}^{\text {cur,max }}$ | (20) |
式中:ξi,t——t时段节点i的电价弹性系数;
ΔPi,t——t时段节点i的响应前后用电需求变化值;
Δρi,t——t时段节点i的电量变化值;
ρpeak,ρvalley——峰、谷电价;
Tpeak,Tvalley——峰、谷时段;
N——配电网总节点数;
储能运行约束条件为
| $0 \leqslant P_{i, t}^{\mathrm{dis}} \leqslant \gamma_{i, t} h_i^{\mathrm{BES}} P_i^{\mathrm{BES}}$ | (21) |
| $0 \leqslant P_{i, t}^{\mathrm{ch}} \leqslant\left(1-\gamma_{i, t}\right) n_i^{\mathrm{BES}} P_i^{\mathrm{BES}}$ | (22) |
| $E_{i, t+t}^{\mathrm{BE}}=E_{i, t}^{\mathrm{BES}}+\left(\eta_i^{\mathrm{ch}} P_{i, t}^{\mathrm{ch}}-\frac{P_{i, t}^{\mathrm{dis}}}{\eta_i^{\text {ids }}}\right) \Delta t$ | (23) |
| $S_{i, \min } h_i^{\mathrm{BES}} E_i^{\mathrm{BES}} \leqslant E_{i, t}^{\mathrm{BES}} \leqslant S_{i, \text { max }} n_i^{\mathrm{BES}} E_i^{\mathrm{BES}} $ | (24) |
| $E_{i, 0}^{\mathrm{BES}}=E_{i, T}^{\mathrm{BES}}$ | (25) |
式中:γi,t——t时段节点i的储能充放电状态;
niBES——节点i的储能数量;
PiBES——节点i的单个储能额定功率;
Δt——调度区间时段;
EiBES——节点i的储能额定容量;
DPV运行约束条件为BES
| $0 \leqslant P_{i, t}^{\mathrm{PV}} \leqslant P_{i, t}^{\mathrm{PV}, \max }$ | (26) |
| $Q_{i, t}^{\mathrm{PV}}=P_{i, t}^{\mathrm{PV}} \tan \varphi_{\mathrm{PV}}$ | (27) |
式中:
φPV—DPV功率因数角。
2.3 模型求解方法
考虑到所建立模型的约束条件中存在随机变量的非线性约束,且决策变量中包含0-1变量和连续变量,具有较强的非凸性,难以使用求解器直接进行求解,因此利用二阶锥松弛技术将非凸问题转凸,进而利用MATLAB平台中的Cplex算法包进行求解。
3 配电网DPV承载能力评估体系
为进一步量化分析高比例DPV对配电网运行水平的影响程度,反映配电网对光伏的承载能力,分别从DPV并网运行特性指标、DPV利用水平和配电网适应性指标3个方面建立DPV承载能力综合评估体系。
首先,DPV并网运行特性指标从配电网运行状态出发,对海量DPV并网后可能发生的风险进行量化分析,从而合理表征其给配电网运行安全带来的影响。由于DPV大量接入配电网后对节点电压的影响最为严重,配电网电压偏差过大会增加功率损耗以及配电网运行的不稳定性,因此提出平均电压偏差G1和最大电压偏差G2。其具体公式如下:
| $G_1=\frac{1}{N} \sum\limits_{i=1}^N \frac{U_i-U_{\mathrm{N}}}{U_{\mathrm{N}}} \times 100 \% $ | (28) |
| $G_2=\frac{U_{\max }-U_{\mathrm{N}}}{U_{\mathrm{N}}} \times 100 \%$ | (29) |
式中:Ui——节点i的实时电压;
Umax——所有节点中实际电压最大值,其值为负指标,值越小配电网接入DPV后对电压的影响越小,配电网运行越安全。
其次,DPV利用水平表示光伏发电功率的利用效率,用于衡量配电网低碳性和DPV消纳量,体现了DPV对配电网的支撑能力。其指标值越大,DPV的利用率越高,配电网用能更清洁。因此,提出DG供电可用率指标G3和DG供电占比率指标G4。其具体公式如下:
| $G_3 =\frac{P_{\mathrm{DG}}^{\mathrm{L}}}{P_{\mathrm{DG}}^{\max }} \times 100 \%$ | (30) |
| $G_4 =\frac{P_{\mathrm{DG}}^{\mathrm{P}}}{P_{\mathrm{all}}} \times 100 \%$ | (31) |
式中:PDGL——DPV可实现消纳的量;
PDGmax——DPV输出功率的最大值;
PDGP——光伏为用户提供的可用电量;
Pall——区域中用户所需的全部用电量。
最后,当DPV大量接入并有效消纳后,配电网线路上的输送功率将会下降。功率下降幅度越大,表明配电网对光伏接入的适应性越强,供电传输能力越好。因此,提出线路平均负载率G5和网损率指标G6作为配电网适应性指标。其具体公式如下:
| $G_5=\frac{\sum\limits_{\mathrm{l}=1}^L P_l}{L P_{\mathrm{N}}} \times 100 \%$ | (32) |
| $G_6=\frac{\sum\limits_{i=1}^N\left(P_{\mathrm{g}, i}+P_{\mathrm{I}}-P_{\mathrm{L}, i}\right)}{\sum\limits_{i=1}^N\left(P_{\mathrm{g}, i}+P_{\mathrm{I}}\right)} \times 100 \%$ | (33) |
式中:L——配电网线路总数;
Pl——第l条线路的实际传输功率;
PN——线路额定传输功率;
Pg,i——节点i的DPV输出功率;
PI——配电网在并网点从上级电网的购电功率,其为负指标,即值越小表明配电网对DPV海量接入的适应性越强;
PL,i——节点i的负荷需求量。
4 算例分析
4.1 基本概况
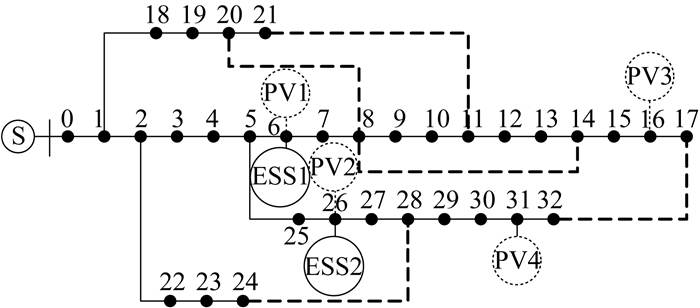
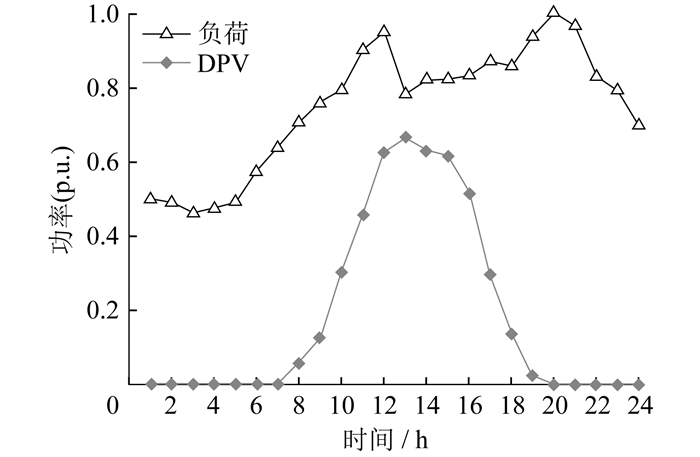
本文选取改进IEEE 33节点配电网[17]进行仿真验证,拓扑结构如图 3所示。其中:虚线为联络线;S为电源;PV1、PV2、PV3、PV4表示DPV;ESS1、ESS2表示储能装置。DPV和负荷的功率预测曲线如图 4所示。
假设该配电网系统中各节点电压标幺值的上、下限依次为1.1 p.u. 和0.9 p.u.,电网的基准容量为10 MVA。储能相关参数如表 1所示,负荷参与DR的分时电价如表 2所示。
表 1
储能相关参数
| 参数 | 数值 |
| 容量/kWh | 1 200 |
| 最大充、放电功率/kW | 250 |
| 最大荷电状态 | 0.90 |
| 最小荷电状态 | 0.10 |
| 初始荷电状态 | 0.15 |
| 充、放电效率 | 0.96 |
| 自放电率 | 0.02 |
表 2
负荷参与DR的分时电价
| 时段类型 | 时段 | 电价/(元/kWh) |
| 峰 | 10:00—15:00 | 0.82 |
| 18:00—21:00 | ||
| 平 | 07:00—10:00 | 0.53 |
| 15:00—18:00 | ||
| 21:00—24:00 | ||
| 谷 | 24:00—07:00 | 0.25 |
4.2 计及不确定性的源荷运行场景生成与分析
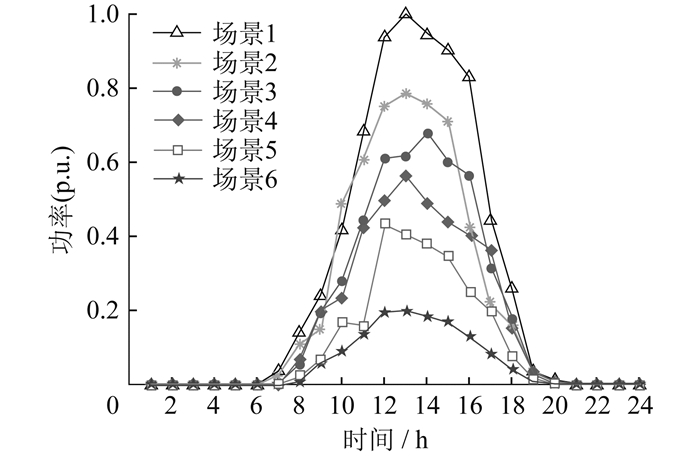
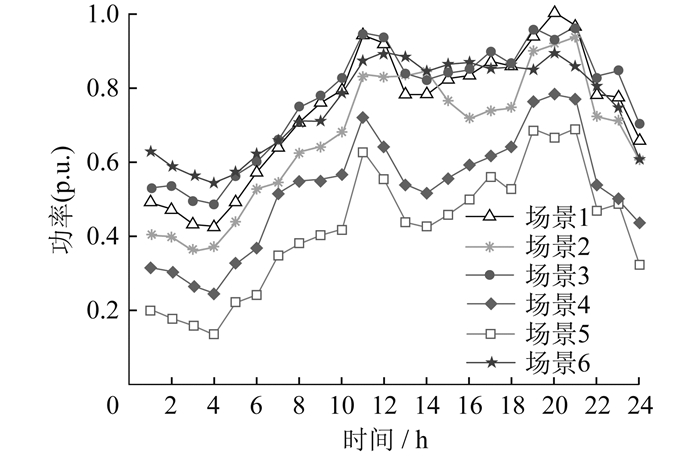
基于源荷不确定性模型,在图 4预测结果的基础上,利用LHS方法生成1 000个负荷与光伏输出功率场景,并通过改进层次K-means算法进行场景削减,得到源荷预测运行场景集。改进层次K-means算法得到光伏输出功率和负荷典型运行场景分别如图 5、图 6所示,对应的典型运行场景概率见表 3。
表 3
改进层次K-means聚类算法的典型运行场景概率
| 场景 | 概率 | 场景 | 概率 | |
| 1 | 0.178 2 | 4 | 0.134 4 | |
| 2 | 0.298 1 | 5 | 0.092 4 | |
| 3 | 0.210 3 | 6 | 0.086 6 |
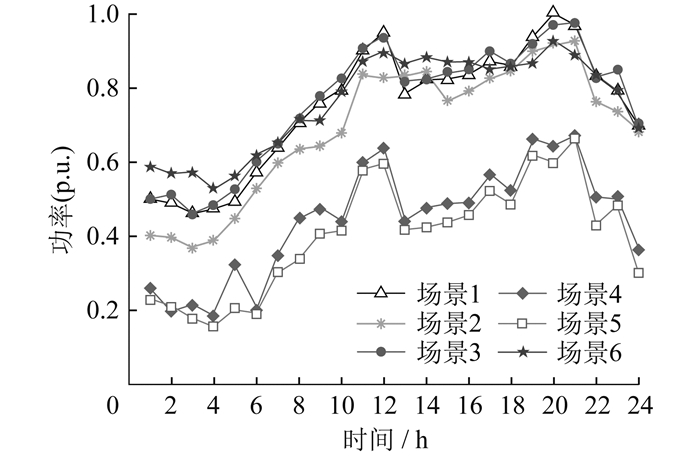
为进一步证明本文所提源荷不确定性模型的有效性与创新性,将其与传统的K-means聚类算法所得源荷预测运行场景进行对比。传统Kmeans聚类算法得到的光伏输出功率和负荷典型运行场景分别如图 7、图 8所示。
由图 5~图 8可知,本文所提方法得到的典型场景具有很好的分层特性,较均匀地包含了从小到大各个层级,有效保留极端场景的同时降低预测误差所带来的影响,可实现对原始数据的准确表征。
为量化本文所提方法的有效性,现引入FM(Fowlkes-Mallows)指数、AR(Adjusted Rand)指数以及分离度(Degree of Separation,DS)3个指标进行验证,具体计算公式见文献[18]。其中:FM指数、AR指数为正指标,值越大表明聚类的结果越接近真实运行水平;DS为负指标,值越小表明簇与簇之间分离得越清晰均匀。不同方法下的指标值计算结果如表 4所示。
表 4
不同方法下的指标值计算结果
| 方法 | FM指数 | AR指数 | 分离度DS |
| 传统K-means聚类算法 | 0.77 | 0.83 | 0.43 |
| 本文所提方法 | 0.94 | 0.95 | 0.17 |
由表 4可知,本文所提方法所得结果在FM指数、AR指数以及DS指标上均优于传统K-means聚类算法,且FM指数和AR指数的值接近于1,而对比2种方法的DS值可以看出,本文所提方法可使源荷运行场景分离得更加清晰均匀,结果更接近真实运行水平,具有显著代表性。
4.3 配电网DPV承载能力评估结果
为体现本文所提方法和模型的适用性与科学性,设置以下4种运行场景进行对比分析。
场景a,仅考虑常规约束条件的影响,不考虑DR以及储能运行约束条件下的配电网新能源承载能力评估,配电网为常规运行方式;
场景b,在考虑常规约束条件影响的基础上,考虑DR约束条件下的配电网新能源承载能力评估;
场景c,在考虑常规约束条件影响的基础上,考虑储能运行约束条件下的配电网新能源承载能力评估;
场景d,在考虑常规约束条件影响的基础上,同时考虑DR以及储能运行约束条件下的配电网新能源承载能力评估,即本文所提方法。
经过仿真运行得到不同场景下DPV接入配电网的最大准入容量如表 5所示。
表 5
不同场景下DPV接入配电网最大准入容量
| 场景 | 最大准入容量 | |||
| PV1 | PV2 | PV3 | PV4 | |
| a | 180 | 230 | 183 | 210 |
| b | 201 | 265 | 210 | 275 |
| c | 213 | 261 | 268 | 306 |
| d | 275 | 419 | 325 | 398 |
由表 5可知,在不同运行场景下,各节点可接入的DPV容量上限具有显著差异性。场景b中各节点接入的光伏容量相较于场景a均有所增强,即DR可以在一定程度上提高配电网的承载能力;场景c中各节点接入的光伏容量相较于场景a也有所提升,且提升幅度比场景b更大,可见配置储能对配电网承载能力的提升效果比需求侧管理更好;场景d的运行结果中,4个节点可接入的DPV容量上限相较于其他3个场景都有显著提升。由此可知,本文所提方法在有效量化评估配电网对DPV承载能力的基础上,可大幅提升配电网的承载能力。
为进一步分析本文所提方法和模型对配电网新能源承载能力以及运行水平的影响,基于配电网DPV承载能力评估体系,计算得到不同场景下配电网DPV承载能力评估结果如表 6所示。
表 6
不同场景下配电网DPV承载能力评估结果
| 场景 | G1 | G2 | G3 | G4 | G5 | G6 |
| a | 3.54 | 4.32 | 78.29 | 15.47 | 79.81 | 5.89 |
| b | 2.98 | 3.77 | 86.56 | 20.53 | 70.25 | 4.76 |
| c | 2.83 | 3.86 | 88.24 | 21.36 | 71.36 | 4.53 |
| d | 1.58 | 2.76 | 97.35 | 29.86 | 65.28 | 2.14 |
由表 6可知,与场景a相比,其他3种场景各指标值均有一定程度的改善。场景b各指标值相较于场景a均有所改善,说明考虑DR后,配电网的承载能力从各方面均得到提升;同理,对比场景c和场景a各指标值可知,单方面考虑储能的调节作用仍可在一定程度上提升配电网对新能源的承载能力;通过对比场景d与其他3个场景各指标值可知,综合考虑DR以及储能运行的影响,可最大程度提升配电网对DPV的承载能力,在并网运行特性、DPV利用水平和配电网综合适应能力各方面均得到了最大程度的优化。以上分析表明本文所提方法和模型在量化评估配电网对DPV承载能力的基础上,可大幅度提升配电网的用能低碳性,并改善电能质量。
5 结语
针对当前海量DPV接入配电网后导致配电网潮流分布变化,配电网电压越限风险增加以及电压分布不均、质量下降等问题,本文提出了一种考虑源荷不确定性的配电网DPV承载能力评估方法,为DPV大规模开发利用以及保证配电网安全低碳运行提供了有效支撑。随着对新型配电系统演变机理和精细化建模的进一步探究,后续可差异化研究配电网对各类清洁能源以及多元化接入体的承载能力,分析各类资源参与电网经济运行和优化调度的应用前景,从而促进新型配电系统的全面发展。
参考文献
-
[1]高漪, 周瑜, 张安龙, 等. 整县光伏下基于个性化联邦学习的光伏出力及负荷功率预测[J]. 电网技术, 2023, 47(11): 4629-4638.
-
[2]董旭柱, 华祝虎, 尚磊, 等. 新型配电系统形态特征与技术展望[J]. 高电压技术, 2021, 47(9): 3021-3035.
-
[3]谢小荣, 贺静波, 毛航银, 等. "双高"电力系统稳定性的新问题及分类探讨[J]. 中国电机工程学报, 2021, 41(2): 461-475.
-
[4]黎博, 陈民铀, 钟海旺, 等. 高比例可再生能源新型电力系统长期规划综述[J]. 中国电机工程学报, 2023, 43(2): 555-581.
-
[5]马钊, 张恒旭, 赵浩然, 等. 双碳目标下配用电系统的新使命和新挑战[J]. 中国电机工程学报, 2022, 42(19): 6931-6945.
-
[6]国家能源局. 分布式电源接入电网承载力评估导则: DL/T 2041—2019[S]. 北京: 中国电力出版社, 2019: 1.
-
[7]董逸超, 王守相, 闫秉科. 配电网分布式电源接纳能力评估方法与提升技术研究综述[J]. 电网技术, 2019, 43(7): 2258-2266.
-
[8]梁志峰, 夏俊荣, 孙檬檬, 等. 数据驱动的配电网分布式光伏承载力评估技术研究[J]. 电网技术, 2020, 44(7): 2430-2439.
-
[9]刘科研, 刘永梅, 盛万兴, 等. 考虑电压约束的分布式电源接入配电网最大准入容量计算方法[J]. 电力自动化设备, 2016, 36(6): 81-87.
-
[10]王强强, 姚良忠, 盛万兴, 等. 基于机会约束规划的配电网分布式光伏承载力提升方法[J]. 电力系统自动化, 2023, 47(18): 132-141.
-
[11]陈璨, 吴文传, 张伯明, 等. 基于多场景技术的有源配电网可靠性评估[J]. 中国电机工程学报, 2012, 32(34): 67-73.
-
[12]赵亮, 黎嘉明, 艾小猛, 等. 光伏出力随机性分量的提取和统计特性分析[J]. 电力系统自动化, 2017, 41(1): 48-56.
-
[13]DOLATABADI A, JADIDBONAB M, MOHAMMADI-IVATLOO B. Short-term scheduling strategy for wind-based energy hub: a hybrid stochastic/IGDT approach[J]. IEEE Transactions on Sustainable Energy, 2019, 10(1): 438-448.
-
[14]王成福, 王昭卿, 孙宏斌, 等. 考虑预测误差时序分布特性的含风电机组组合模型[J]. 中国电机工程学报, 2016, 36(15): 4081-4090.
-
[15]高亚静, 朱静, 程华新, 等. 计及不确定性因素基于多场景的主动配电系统短期供电能力评估[J]. 中国电机工程学报, 2016, 36(22): 6076-6085.
-
[16]YU P, WAN C, SONG Y. Distributed control of multi-energy storage systems for voltage regulation in distribution networks: a back-and-forth communication framework[J]. IEEE Transactions on Smart Grid, 2020, 12(3): 1964-1977.
-
[17]黄鸣宇, 张庆平, 张沈习, 等. 高比例清洁能源接入下计及需求响应的配电网重构[J]. 电力系统保护与控制, 2022, 50(1): 116-123.
-
[18]陈聿, 田博今, 彭云竹, 等. 联合手肘法和期望最大化的高斯混合聚类电力系统客户分群算法[J]. 计算机应用, 2020, 40(11): 3217-3223.