|
|
|
发布时间: 2024-12-28 |
智能电网技术 |
|
|
|
收稿日期: 2024-03-29
中图法分类号: F426.61
文献标识码: A
文章编号: 2096-8299(2024)06-0587-08
|
摘要
日前电价的准确预测对于提高市场主体的交易收益至关重要。针对高比例新能源参与现货市场交易导致日前电价预测难度增加的问题,提出了一种基于相似波动聚类与自注意力(SA)机制的轻型量梯度提升机(SA-LightGBM)日前电价预测方法。首先,基于电价数据特征,采用改进模糊C均值(FCM)聚类对波动场景进行分类,得到3种波动场景下的数据集。其次,在不同波动场景下,采用Kendall相关系数对影响电价的特征进行相关性分析,选定输入特征。然后,基于波动场景与输入特征建立SA-LightGBM预测模型。最后,利用国内某省电力交易平台提供的历史数据,验证了所提模型的有效性和可靠性。
关键词
日前电价预测; 模糊C均值; Kendall相关系数; 自注意力机制; 轻型量梯度提升机
Abstract
The precise forecasting of electricity prices for the following day holds significant importance in enhancing the revenue generated by market participants. Addressing the challenge posed by the increased presence of new energy sources in spot market transactions, a novel approach for predicting day-ahead electricity prices using light gradient boosting machine (LightGBM) is introduced. The method incorporates similar wave clustering and self-attention (SA) techniques. Initially, fuzzy C-means (FCM) clustering is applied to categorize fluctuation scenarios based on electricity price data characteristics, resulting in distinct datasets for each scenario. Subsequently, Kendall correlation coefficient is utilized to analyze the correlation of features influencing electricity prices across different fluctuation scenarios, facilitating the selection of input features. The SA-LightGBM prediction model is then constructed, tailored to the specific fluctuation scenario and input characteristics. Finally, the proposed algorithm's effectiveness and dependability are assessed using historical data sourced from a provincial power trading platform in China.
Key words
day-ahead electricity price prediction; fuzzy c-means; Kendall correlation coefficient; self-attention; light gradient boosting machine
随着全球电力市场化改革的不断深入,电力市场的格局逐渐从集中式购买转变成自由化交易模式[1]。在电力市场中,电价作为最关键的因素之一,直接关系到工业生产、资源布局以及人民生活。电价数据通常具有较强的时序性和周期性[2],尤其在新能源占比逐渐升高的电力市场中,易出现电价随机波动情况,使得电价预测变得更为困难[3]。
经过长时间的迭代更新和应用,目前的电价预测模型可分为统计预测法和机器学习预测法[4]。统计预测法借助数学方法建立统计模型,通过分析历史数据进行预测[5]。文献[6]采集了某国的日平均电价,并将发电量作为特征变量,利用最小二乘法预测日平均电价。文献[7]从确定性短期风能预测出发,基于统计学原理建立了风速(功率)与历史时间序列间的关系模型。统计预测法具有拟合非线性数据效果差、容易出现过拟合以及无法阐述变量内部相关性影响等问题[8],而作为人工智能领域的核心组成部分,机器学习预测法能够更灵活地适应复杂的非线性关系[9]。文献[10]采用基于长短期记忆(Long Short-Term Memory,LSTM)神经网络方法处理电力市场日前电价预测,提出将特征向量以时序序列方式构造并作为LSTM网络模型输入数据,从而较好拟合了负荷数据的时序性和复杂非线性关系。文献[11]通过引入遗传算法对极限学习机进行点优化,突破了随机生成参数预测精度不高和波动性大等问题,表现出更高的预测精度和稳定性。文献[12]建立了一种引入相关系数的粒子群优化算法(Particle Swarm Optimization,PSO)电价预测模型,PSO模型会根据负荷与电价的相关系数判断是否引入负荷因素,避免了将过多不相关的负荷因素引入模型中,能够更精准地利用负荷信息提高预测精度。
传统机器学习预测法具有参数量和调参工作量大,容易过拟合等缺点。而基于轻型梯度提升机(Light Gradient Boosting Machine,LightGBM)的机器学习预测法通过特征并行、直方图学习和按层构建等技术,有效解决了以上问题。文献[13]尝试利用基于最大信息系数的特征选择算法和LightGBM分类器构建暂态稳定评估模型,从而有效降低了评估模型的输入特征维度和计算复杂度,显著提高了评估模型的数据处理时间,保证了模型在线应用的时效性。文献[14]提出一种基于LightGBM的独立循环神经网络(Independently Recurrent Neural Network,IndRNN)日前电价预测方法,采用LightGBM方法筛选出影响日前电价的关键因素,避免冗余信息数据对预测结果的影响,又充分结合了IndRNN模型极强的时间序列处理能力,有效提高了日前电价预测模型的精度,更适用于波动性较大的日前电价预测。文献[15]采用线性模型与非线性模型组合预测方法,不仅可以挖掘长时间数据间的内在联系,还可以避免非连续性特征对预测精度的不良影响,降低极端场景下的预测误差,具有更稳定的预测效果。文献[16]在保留对时序数据总体感知的同时,考虑了非连续性特征的有效信息,具有更高的预测精度和适用性。文献[17]研究发现,采用LightGBM机器学习预测法能够高效、并行训练特征及处理海量数据,其基于树模型的训练过程具有很强的可解释性和可优化性。
但以上方法仍存在特征选取不全面、预测场景未分类与对尖峰电价和深谷电价不敏感等问题。为解决上述问题,本文提出了一种基于相似波动聚类与自注意力(Self-Attention,SA)机制的LightGBM日前电价预测方法。首先,采用模糊C均值(Fuzzy C-Means,FCM)算法对波动场景进行分类,针对FCM算法易受噪声影响的问题,加入自适应权重,并将原本的欧氏距离替换为马氏距离,以提高聚类有效性。其次,利用Kendall相关系数对影响电价的因素进行相关性分析,选出不同场景下影响电价的因素。最后,构建基于SA-LightGBM的日前电价预测模型。
1 基于FCM算法的相似波动聚类
受外部因素影响,电价序列波动容易导致日前电价预测不准确。因此,本文采用改进FCM算法对相似波动曲线进行聚类,将波动场景划分为少量波动、中幅波动与大量波动,得到相似波动状态下的数据集合,以分别构建并训练预测模型。
1.1 FCM算法
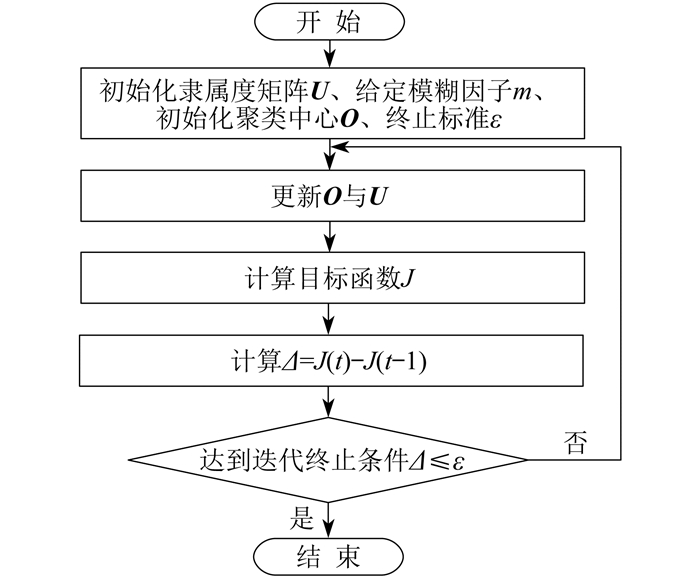
相较于硬聚类算法,软聚类FCM算法融合模糊理论,采用隶属度表示数据之间的关系,从而确定数据的所属聚类簇。FCM算法通过优化目标函数得到样本点与所有聚类中心的隶属度,并通过迭代更新隶属度与聚类中心提升聚类效果,从而实现对数据的自动分类。FCM算法流程如图 1所示。其中,Δ为第t次和第t−1次循环的差值。
FCM算法的目标函数采用C均值函数,对于给定数据集X=[x1,x2,x3,…xi,…,xn],i=1,2,3,…,n,n代表给定数据集的样本个数。FCM算法表达式J为
| $ J=\sum\limits_{i=1}^n \sum\limits_{j=1}^k u_{i j}^m d_{i j}^2 $ | (1) |
| $ u_{i j}=\frac{1}{\sum\limits_{z=1}^c\left(\frac{d_{i j}}{d_{i z}}\right)^{\frac{2}{m-1}}} $ | (2) |
| $ d_{i j}=\left\|x_i-v_j\right\| $ | (3) |
| $ v_j=\frac{\sum\limits_{i=1}^n u_{i j}^m x_i}{\sum\limits_{i=1}^n u_{i j}^m} $ | (4) |
| $ \sum\limits_{j=1}^k u_{i j}=1, \quad u_{i j} \in[0, 1] $ | (5) |
式中:k——聚类中心个数;
uij——第i个样本属于第j个聚类中心的隶属度;
m——模糊因子,取2;
c——聚类个数;
dij——第i个样本属于第j个聚类中心的距离;
diz——第i个样本属于第z个聚类中心的距离;
vj——第j个聚类中心。
1.2 马氏距离
传统欧氏距离只能表达两个数据点之间的直线距离,而电价特征间存在大量的相关性联系,欧氏距离不仅无法体现相关性,而且有时会错误表达数据点到聚类中心的距离。因此,本文采用马氏距离。马氏距离通过计算数据的协方差距离,可以有效考虑各种特性之间的联系,表示两个位置样本集的相似度。
假设 x、y是从总体G中随机抽取的两个样本,则x与y之间的马氏距离du2(x,y) 为
| $ d_u^2(\boldsymbol{x}, \boldsymbol{y})=(\boldsymbol{x}-\boldsymbol{y})^{\mathrm{T}} {\boldsymbol{\varPhi}}^{-1}(\boldsymbol{x}-\boldsymbol{y}) $ | (6) |
式中:u——总体G的维数;
Φ——协方差矩阵。
1.3 自适应权重
在平稳数据集下,经典FCM算法聚类效果良好,而电价数据往往存在噪声与数据不均衡分布的情况,FCM算法抗噪声能力差,易导致聚类结果不理想。通过分解式(1)得到
| $ J=\sum\limits_{i=1}^n \sum\limits_{j=1}^k u_{i j}^m d_{i j}^2=\sum\limits_{j=1}^k u_{1 j}^m d_{1 j}^2+\sum\limits_{j=1}^k u_{2 j}^m d_{2 j}^2+\ldots+\sum\limits_{j=1}^k u_{n j}^m d_{n j}^2 $ | (7) |
可以看出,每个样本点对聚类中心的贡献度相同,且在每次迭代过程中没有变化,显然不符合实际情况。因此,本文在FCM算法计算流程中加入自适应权重,通过两个自适应权重向量ζ和η控制样本点与聚类中心的权重,ζ用于确定样本点相较于聚类中心的权重,η用于确定不同迭代次数下样本点的权重。通过设立自适应权重,可以判断不同样本点的重要性,有利于减弱FCM算法对减噪声的干扰。加入自适应权重向量的目标函数为
| $ J=\sum\limits_{i=1}^n \sum\limits_{j=1}^k \boldsymbol{\eta}_{i j} \zeta^t u_{i j}^m d_{i j}^2 $ | (8) |
式中:t——迭代次数。
2 电价影响因素分析
日前电价中的电价受许多外界因素影响,如日前统调负荷、日前新能源负荷、日前联络线计划总加、非市场化机组出力、检修总容量等,且在不同波动场景下的影响因素不同[18]。因此,本文采用Kendall相关系数对不同场景下的电价影响因素进行相关性分析。通过Kendall相关系数选出不同波动场景下的输入特征,作为随后构建模型的铺垫。
Kendall相关系数是基于样本数据对间的关系进行相关性强弱分析。其值越接近1,表示正相关越大;其值越接近于−1,则表示负相关越大。Kendall相关系数K的表达式为
| $ K=\frac{C-D}{\frac{1}{2} n(n-1)} $ | (9) |
式中:C——一致对数目;
D——非一致对数目。
当变量P中P1、P2样本对与Q中Q1、Q2样本对满足P1 < Q1与P2 < Q2时,称这两个样本对一致,否则为非一致。
利用国内某省电力交易平台提供的历史数据,研究不同波动场景下的Kendall相关系数,具体如表 1所示。
表 1
不同波动场景下的Kendall相关系数
| 波动场景 | Kendall相关系数 | ||||
| 日前统调负荷 | 日前新能源负荷 | 日前联络线计划总和 | 非市场化机组输出功率 | 检修总容量 | |
| 少量波动 | 0.679 | -0.632 | 0.542 | -0.092 | 0.102 |
| 中幅波动 | 0.657 | -0.668 | 0.489 | -0.121 | 0.301 |
| 大量波动 | 0.681 | -0.679 | 0.428 | -0.319 | 0.342 |
由表 1可知,在少量波动场景下,日前统调负荷、日前新能源负荷与日前联络线计划总和的相关系数最大,可为输入特征;在中幅波动场景下,需要在少量波动场景下的特征上加入检修总容量;在大量波动场景下,需将提及的所有影响因素作为特征。
3 基于SA-LightGBM的日前电价预测模型
3.1 LightGBM算法
LightGBM是一种基于梯度增强决策树(Gradient Boosting Decision Tree,GBDT)的改进算法,相较于GBDT算法中采用弱分类器(决策树)进行迭代训练,LightGBM利用boosting思想生成强分类器,具有训练速度更快、内存消耗更低和准确率更好的优点。相较于GBDT,LightGBM算法主要有以下3点改进。
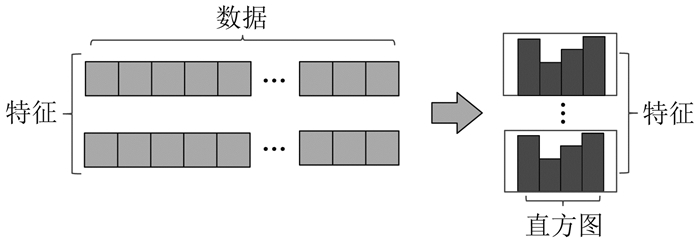
首先,采用直方图加速算法寻找最优分割点,简化计算过程,减少内存占用。该算法主要思想为:将连续的浮点特征值离散为b个整数和1个宽度为b的直方图。直方图形成过程如图 2所示。
在遍历数据过程中,以离散化后的值为指针在直方图中累计统计量。当累积到需要的统计量时,根据直方图离散值,遍历寻找最优分割点。
其次,采用基于梯度的单边采样(Gradient-Based One-Side Sampling,GOSS)算法减少样本数量。该算法主要思想为:采用样本梯度信息考量样本重要性,保留梯度较大的样本点,而针对梯度较小的样本点进行随机采样。这样既主要学习大梯度样本的信息,又不遗漏小梯度样本点的信息,在不改变原始数据分布的同时,既减小了样本数量,又提升了训练速度。
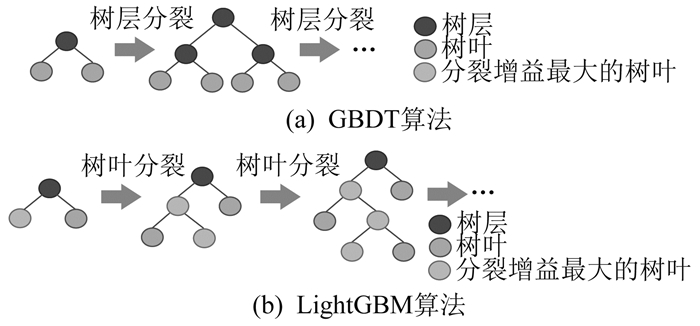
最后,采用带深度限制的按树叶生长策略避免过拟合。在学习过程中,GBDT算法采取按树层生长,即每次迭代中会遍历整个数据集,虽有遍历完全性,但会产生许多不必要的搜索,增加计算成本。而LightGBM算法采用按树叶生长,虽然可以降低计算成本和迭代误差,但会产生较深的决策树,因此引入深度限制,从而避免过拟合。两种算法的生长策略如图 3所示。
3.2 SA机制
SA机制属于注意力机制的变体,主要针对网络中多个内相关输入无法构建相关性的问题,通过注意输入数据内部的相关性,减少对外部信息的依赖,实现记忆功能。SA机制F的表达式为
| $ F(\boldsymbol{Q}, \boldsymbol{K}, \boldsymbol{V})=\operatorname{softmax}\left(\frac{\boldsymbol{Q} \boldsymbol{K}^{\mathrm{T}}}{\sqrt{d_{\mathrm{c}}}}\right) \boldsymbol{V} $ | (10) |
式中:Q、K、V——同一输入经矩阵变化得到的查询矩阵、键矩阵和值矩阵;
dc——保持梯度稳定的缩放因子;
softmax——激活函数。
SA机制主要计算步骤如下。
步骤1 对于给定数据集X=[x1,x2,x3,…,xn],分别乘以查询权重矩阵Wq、键权重矩阵Wk以及值权重矩阵Wv,得到Q、K、V为
| $ \boldsymbol{Q}=\boldsymbol{W}_{\mathrm{q}} \boldsymbol{X} $ | (11) |
| $ \boldsymbol{K}=\boldsymbol{W}_{\mathrm{k}} \boldsymbol{X} $ | (12) |
| $ \boldsymbol{V}=\boldsymbol{W}_{\mathrm{v}} \boldsymbol{X} $ | (13) |
步骤2 计算SA机制中的置换矩阵A为
| $ \boldsymbol{A}=\boldsymbol{K}^{\mathrm{T}} \boldsymbol{Q} $ | (14) |
步骤3 对矩阵A进行softmax操作,得到矩阵A′为
| $ \boldsymbol{A}^{\prime}=\operatorname{softmax}(\boldsymbol{A}) $ | (15) |
步骤4 计算输出向量B为
| $ \boldsymbol{B}=\boldsymbol{A}^{\prime} \boldsymbol{V} $ | (16) |
在预测过程中,SA机制会关注输入特征序列之间的特征信息,联系全局与局部的关系,更好把握序列变化趋势。
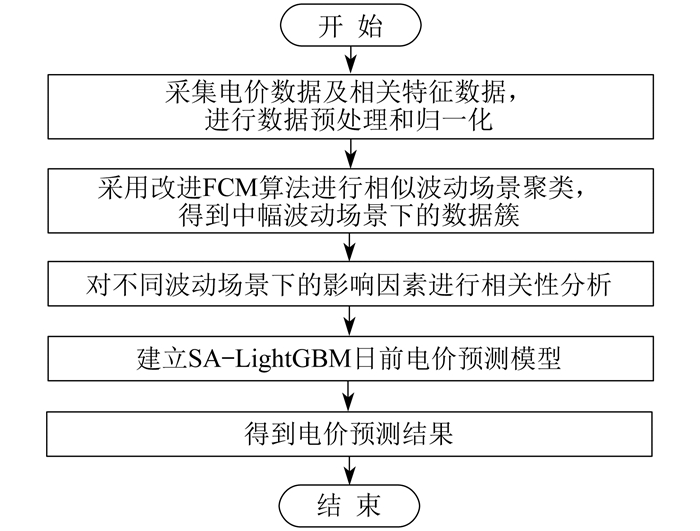
3.3 日前电价预测流程
基于SA-LightGBM的日前电价预测流程如 图 4所示。
3.4 预测评价指标
本文采用平均绝对误差MAE、均方误差MSE、均方根误差RMSE、平均绝对百分比误差MAPE评价电价预测结果。这些评价指标越小,则表示预测效果越好。各评价指标表达式为
| $ M_{\mathrm{AE}}=\frac{1}{n} \sum\limits_{i=1}^n\left|\hat{y}_i-y_i\right| $ | (17) |
| $ M_{\mathrm{SE}}=\frac{1}{n} \sum\limits_{i=1}^n\left(\hat{y}_i-y_i\right)^2 $ | (18) |
| $ R_{\mathrm{MSE}}=\sqrt{\frac{1}{n} \sum\limits_{i=1}^n\left(\hat{y}_i-y_i\right)^2} $ | (19) |
| $ M_{\mathrm{APE}}=\frac{1}{n} \sum\limits_{i=1}^n\left|\frac{\hat{y}_i-y_i}{y_i}\right| \times 100 \% $ | (20) |
式中:
yi——实际值。
4 算例分析
4.1 数据处理
本文选取2021年国内某省电力交易平台提供的历史数据为数据集。该数据集采样时间间隔为15 min。本文采用最小二乘法对采集的数据进行空缺数据填补,其表达式f(x)为
| $ f(x)=a_1 r_1(x)+a_2 r_2(x)+a_3 r_3(x)^{-1}+\cdots a_p r_p(x) $ | (21) |
式中:ap——待定系数;
rp(x)——事先选定的一组线性无关函数。
对所有数据进行归一化,其表达式为
| $ Y=\frac{Y-Y_{\min }}{Y_{\max }-Y_{\min }} $ | (22) |
式中:Y——需要归一化的数据;
Ymax——输入最大值;
Ymin——输入最小值。
4.2 相似波动场景聚类结果分析
4.3 日前电价预测结果对比
本文在相似波动场景分类结果中各选择1 d为典型日进行预测。为验证所提模型的优劣性,将其与LightGBM、SA-Xgboost、SA-Catboost、LSTM 4种模型进行对比。其中,SA-Xgboost、SA-Catboost皆为SA优化的boosting模型,而LSTM为深度学习模型。
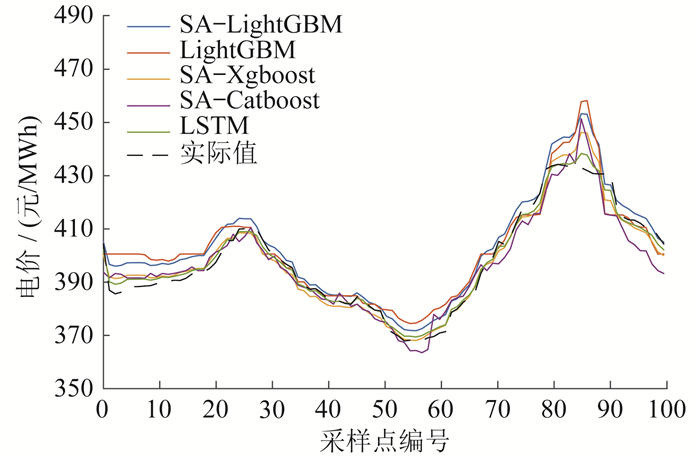
4.3.1 少量波动场景下预测结果
少量波动场景下的预测结果如图 6所示。
由图 6可以看出,5种模型均表现出良好的效果,而SA-LightGBM更接近实际值。
少量波动场景下5种模型评价指标如表 2所示。
表 2
少量波动场景下5种模型评价指标
| 预测模型 | MAE/元 | MSE/元2 | RMSE/元 | MAPE/% |
| SA-LightGBM | 8.48 | 115.62 | 10.75 | 2.2 |
| LightGBM | 8.95 | 144.48 | 12.02 | 4.1 |
| SA-Xgboost | 8.77 | 127.69 | 11.23 | 2.7 |
| SA-Catboost | 9.12 | 172.92 | 13.15 | 4.5 |
| LSTM | 8.12 | 107.25 | 10.35 | 1.9 |
由表 2可以看出,几种模型的4个评价指标都较为接近,LSTM的所有指标最低,这是因为LSTM针对较为平稳的序列效果较好。而SA-LightGBM与LSTM的结果相差不多,且在3种boosting模型中的指标均为最低,RMSE指标相比LightGBM低10.6%,相比SA-Xgboost低4.27%。由此可知,采用SA改进后的LightGBM模型比3种boosting模型在少量波动场景下表现更好。
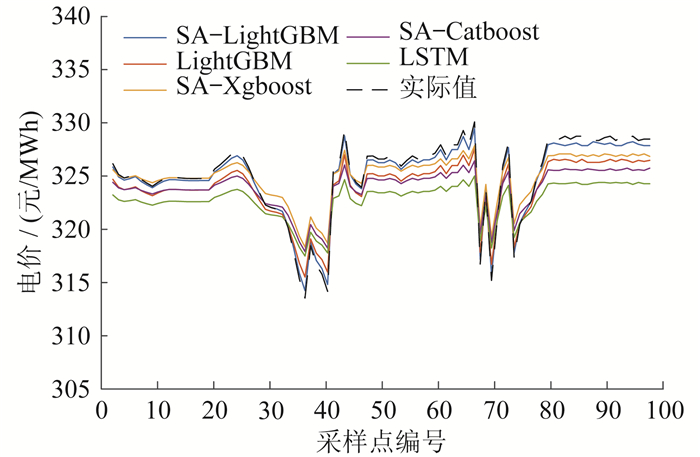
4.3.2 中幅波动场景下预测结果
在中幅波动场景下,序列存在部分波动情况且范围较小,因此会影响预测精度。中幅波动下的预测结果如图 7所示。
由图 7可知,SA-LightGBM在平稳状态下与实际值几乎相近,而在波动出现时,其预测趋势更切合实际。
中幅波动场景下5种模型评价指标如 表 3所示。
表 3
中幅波动场景下5种模型评价指标
| 预测模型 | MAE/元 | MSE/元2 | RMSE/元 | MAPE/% |
| SA-LightGBM | 7.26 | 105.93 | 10.29 | 2.7 |
| LightGBM | 12.05 | 155.87 | 25.61 | 5.1 |
| SA-Xgboost | 8.78 | 150.06 | 12.25 | 3.8 |
| SA-Catboost | 8.24 | 138.77 | 11.78 | 3.3 |
| LSTM | 9.01 | 166.15 | 12.89 | 4.2 |
由表 3可知,SA-LightGBM的各项指标相较其他模型最低,在MAE上比SA-Xgboost低17.3%,比SA-Catboost低11.9%;在RMSE上比SA-Xgboost低16%,比SA-Catboost低12.6%,比LSTM低20.2%。因此,在中幅波动场景下,SA-LightGBM预测效果最好。
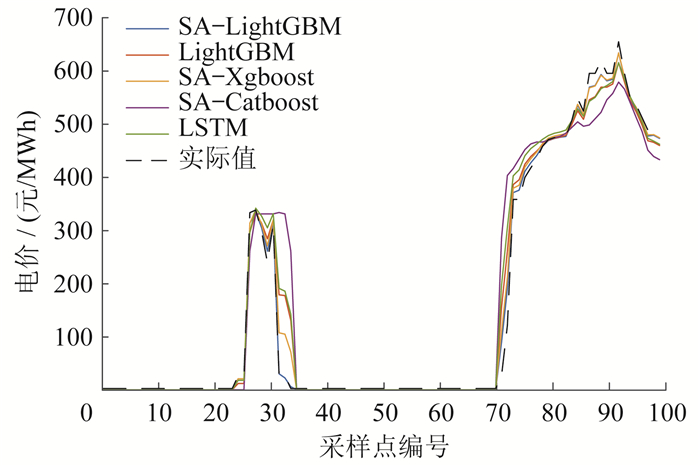
4.3.3 大量波动场景下预测结果
在大量波动场景下,由于序列中出现急促波动且波动范围较大,因此会显著增加预测难度。该场景下的预测结果如图 8所示。
由图 8可知,SA-LightGBM模型在大波动段能更好地学习波动趋势,在波动处的预测更符合实际值。
大量波动场景下5种模型评价指标如表 4所示。
表 4
大量波动场景下5种模型评价指标
| 预测模型 | MAE/元 | MSE/元2 | RMSE/元 | MAPE/% |
| SA-LightGBM | 10.11 | 136.45 | 11.68 | 2.7 |
| LightGBM | 11.79 | 194.18 | 13.93 | 3.1 |
| SA-Xgboost | 11.23 | 172.13 | 13.12 | 3.1 |
| SA-Catboost | 12.02 | 228.92 | 15.13 | 3.7 |
| LSTM | 11.76 | 176.10 | 13.27 | 3.2 |
由表 4可知,在MAPE上,由于SA-Xgboost对局部学习的能力优于SA-LightGBM,所以SA-Xgboost在大量波动场景下预测结果最好。但SA-LightGBM在MAE上相比于LSTM低14%,相比于SA-Xgboost低10%;在RMSE上相比于LSTM低12%,相比于SA-Xgboost低11%,因此SALightGBM模型在大量波动场景下预测效果最好。
5 结论
针对高比例新能源参与现货交易导致日前电价预测难度增加的问题,本文构建了一种基于相似波动聚类与SA-LightGBM模型的日前电价预测模型,得出以下结论。
(1)采用改进FCM算法,通过改欧氏距离为马氏距离并引入自适应权重,减小了噪声数据对FCM算法的影响,提高了聚类准确度和不同场景下的预测精度。
(2)通过Kendall相关系数判断每种场景下影响电价的因素,并选择不同的特征,可以准确描述影响状态,提高预测真实性。
(3)与4种预测模型相比,SA-LightGBM模型在不同波动场景下的预测效果均为最佳,具有良好的适应性。
参考文献
-
[1]吉兴全, 曾若梅, 张玉敏, 等. 基于注意力机制的CNN-LSTM短期电价预测[J]. 电力系统保护与控制, 2022, 50(17): 125-132.
-
[2]韩升科, 胡飞虎, 陈之腾, 等. 基于GCN-LSTM的日前市场边际电价预测[J]. 中国电机工程学报, 2022, 42(9): 3276-3286.
-
[3]殷豪, 曾云, 孟安波, 等. 基于奇异谱分析的短期电价预测[J]. 电力系统保护与控制, 2019, 47(1): 115-122.
-
[4]SALIH G, UMUT U, ILKAY O. Transfer learning for electricity price forecasting[J]. Sustainable Energy, Grids and Networks, 2023, 34: 100996. DOI:10.1016/j.segan.2023.100996
-
[5]MIN Y, WEI X, LI M. Short-term electricity price forecasting based on BP neural network optimized by SAPSO[J]. Energies, 2021, 14(20): 6514-6518. DOI:10.3390/en14206514
-
[6]谢诗宇. 基于统计学习的电价预测模型[J]. 通讯世界, 2018(5): 287-288.
-
[7]赵泽妮, 云斯宁, 贾凌云, 等. 基于统计模型的短期风能预测方法研究进展[J]. 太阳能学报, 2022, 43(11): 224-234.
-
[8]IOANNIS A A, DIMITRIOS B, DIMITRIOS K, et al. Optimized data-driven models for short-term electricity price forecasting based on signal decomposition and clustering techniques[J]. Energies, 2022, 15(21): 7929-7939.
-
[9]VASUDHARINI S, MING J T, XING P L. Wholesale electricity price forecasting using integrated long-term recurrent convolutional network model[J]. Energies, 2022, 15(20): 7606-7609.
-
[10]陆继翔, 张琪培, 杨志宏, 等. 基于CNN-LSTM混合神经网络模型的短期负荷预测方法[J]. 电力系统自动化, 2019, 43(8): 131-137.
-
[11]郑健, 曹炜. 基于GA-ELM神经网络的日前电价预测[J]. 上海电力学院学报, 2018, 34(1): 90-94.
-
[12]李娜, 李郁侠, 王丽霞, 等. 引入电价与负荷相关系数的PSO-BP神经网络电价预测模型[J]. 水力发电学报, 2010, 29(1): 219-222.
-
[13]周挺, 杨军, 周强明, 等. 基于改进LightGBM的电力系统暂态稳定评估方法[J]. 电网技术, 2019, 43(6): 1931-1940.
-
[14]段央央, 陈光宇, 张仰飞, 等. 基于LightGBM-IndRNN模型的现货市场日前电价预测[J]. 水力发电, 2023, 49(1): 84-87.
-
[15]陈纬楠, 胡志坚, 岳菁鹏, 等. 基于长短期记忆网络和LightGBM组合模型的短期负荷预测[J]. 电力系统自动化, 2021, 45(4): 91-97.
-
[16]GLORIA A B, ANGELICA G, FILIPPO G D, et al. Forecasting electricity prices with expert, linear, and nonlinear models[J]. International Journal of Forecasting, 2023, 39(2): 570-586.
-
[17]袁枫, 梁羽佳. 基于粒子群算法的BP神经网络电价预测系统设计[J]. 集成电路应用, 2022, 39(4): 132-133.
-
[18]姚子麟, 张亮, 邹斌, 等. 含高比例风电的电力市场电价预测[J]. 电力系统自动化, 2020, 44(12): 49-55.