|
|
|
发布时间: 2019-06-10 |
|
|
|
|
收稿日期: 2019-04-03
基金项目: 国家社会科学基金青年项目(15CJY058)
中图法分类号: F752.6
文献标识码: A
文章编号: 1006-4729(2019)03-0284-09
|
摘要
构建了具有中国能源价格特征的一般均衡(CGE)模型。首先将工业行业依据能源消耗密度分类为高能耗行业和低能耗行业两大类; 然后模拟设计了在两种不同技术水平条件下的两种能源价格市场化方案; 最后测算4种情境下能源价格波动可能对中国高、低能耗工业行业出口的差异化影响。结果发现:中国能源价格波动对高能耗工业行业出口的影响幅度大于对低能耗工业行业的影响; 高技术进步水平下, 中国能源价格市场化对高、低能耗工业行业出口的影响比现有技术水平下的影响要小。
关键词
能源价格市场化; 高能耗行业; 出口; 一般均衡模型
Abstract
A computable general equilibrum (CGE) model with Chinese energy price character is constructed.First, the industry is classified into high energy consumption industry and low energy consumption industry based on the energy consumption density.Based on the formation characteristics of China's energy prices, the energy price is assumed to be external in the model.The research simulates two ways of energy price marketization schemes with two different technology situations.Under these four scenarios, the study calculates the different impact of energy price volatility on China's high and low energy consumption industries.The study concludes that the impact of upward or downward fluctuations in China's energy prices on the export of high energy consumption industries is greater than its impact on low energy consumption industries regardless of the level of technology.After the progress of technology, the impact of China's energy price fluctuations on the export of high or low energy consumption industries is smaller than the situation of current technology situation.Finally, the study puts forward policy recommendations to improve the export competitiveness of China's high and low energy consumption industrial industries based on the outcome of research from the perspective of optimizing the export structure and upgrading the industry's energy-saving technologies.
Key words
energy price marketization; high energy consumption industries; export; Computable General Equilibrum model
出口贸易为改革开放三十多年来的中国经济发展做出了巨大贡献, 特别是在中国加入世界贸易组织之后, 2001年至2016年期间, 中国出口贸易对GDP的贡献程度平均高达25.7%, 且呈现先上升后下降的趋势。2006年出口贸易对经济贡献的比重达到高峰, 为35.3%, 此后逐年下降, 2016年为18.6%。其中, 工业品出口对我国出口贸易的发展起着决定性作用。
当前中国的经济发展处于历史转折期, 2016年人均GDP达8 016$, 按世界银行的标准划分处于中等偏上收入国家水平, 简单地继续依赖高能耗和劳动密集型行业发展已难以满足中国经济向高收入国家迈进的需求。针对中国能否跳脱所谓的中等收入国家陷阱, 以及出口贸易能否持续支撑中国经济增长等问题, 工业品出口贸易能否成功升级转型将是一个至关重要的决定因素。改革开放以来, 基于不同时期经济发展的客观需要和中国能源供求的客观情况, 政府在能源价格形成机制上一直不断地努力探索和改进, 先后出台了关于能源价格体制改革的多项政策文件, 不断优化各类能源品种的定价方式和管理机制, 切实推动了能源市场化改革的进程。但总体而言, 现阶段中国主要能源品种的价格形成机制仍属于政府管制模式, 以政府定价和垄断性价格为主, 少部分能源品种已基本实现由市场定价。这种政府管制下的定价机制使得中国能源价格与国际能源价格相比, 不仅存在一定的静态相对差异。也存在明显的动态波动差异。中国能源价格波动较国际能源价格波动整体更为平缓。根据杨迎春等人[1]的研究结论, 中国前期的能源价格机制为出口贸易的快速发展做出了巨大的贡献, 政府管制下的能源价格使国内的企业获取了相对于国际市场的能源要素成本优势, 促进了整体出口规模的快速增长, 特别是高能耗工业行业出口的发展。
近年来, 随着国内外对于节能减排政策的提出, 中国政府一直致力于通过一系列的措施对能源价格的形成进行市场化改革, 能源生产的上中游价格已基本放开, 原煤、原油逐渐实现市场化, 虽然终端能源价格仍然受到政府不同程度的管制, 但未来完全市场化定价的改革趋势已经形成。在这样的背景下, 中国通过依靠国内外能源价格差异获得的出口比较优势未来势必会受到一定的冲击。如何基于国内能源价格市场化改革的趋势, 制定更加契合中国出口贸易转型升级的政策措施是当前政策研究者应当关注的焦点[2]。因此, 本文将从当前能源价格扭曲对中国出口贸易产生影响的研究开始, 尝试模拟未来取消终端能源价格政府管制的情景, 分析各主要能源品种均实现市场化定价后将对中国高、低能耗工业行业出口贸易产生的差异化影响, 从而为中国出口贸易结构升级转型提供更加科学的对策。
1 相关研究现状及评述
1.1 能源价格影响出口贸易的研究
近年来, 学术界对能源价格影响出口贸易的研究主要包括两大类。
(1) 运用传统的计量分析方法定量分析研究能源价格对出口贸易的影响。如陈刚等人[3]在定义能源约束量化指标的基础上, 建立了能源价格约束对出口贸易结构影响的动态计量模型, 结果表明, 短期内能源约束通过直接的价格冲击和间接的生产要素转移, 可以带动贸易结构的优化; 从长期看, 能源约束对出口贸易结构的调整方向具有不确定性。江静等人[4]基于国际标准产业分类的分析表明, 能源价格的提高会对除炼焦和精炼石油制品以外的其他几乎所有行业出口的竞争力带来负面影响, 且影响幅度存在一定的差异。杨迎春等人[1]定量分析了国内外能源相对价格对中国出口规模的短期和长期影响。ABIMANYU Y[5]检验了2012—2016年印度尼西亚的油价变动与出口额的相关性, 发现两者之间具备正向关系。
(2) 将抽象的理论形式转变成一个可计算的关于现实的经济模型, 即一般均衡(Computable General Equilibrium, CGE)模型, 用于核算能源价格对出口贸易的影响。如胡宗义等人[6]通过CGE模型, 模拟2005—2010年期间能源价格提高对中国经济的影响情况, 发现能源价格的提高会对宏观经济产生较大的负面影响, 短期和长期内均会导致出口贸易额的下降。LEVENT A等人[7]运用CGE模型, 基于全球贸易分析项目(Global Trade Analysis Project, GTAP)的数据, 发现不论是在低油价、标准油价还是高油价的情境下, 油价的冲击都不利于出口贸易, 造成贸易账户的恶化。高志远[8]运用CGE模型模拟了各类能源价格分别上涨5%和10%对经济的影响, 发现能源价格上涨将减少各行业的贸易出口。
1.2 定量分析能源价格波动对中国经济的影响
定量分析能源价格波动对中国经济的影响是一个复杂的系统工程, 在变量的选取上难免存在很多局限, 且分析过程中无法顾及经济系统的整体变化, 使研究结论具有很大的不确定性。本文拟采取CGE模型进行研究, 并从以下3个方面进行改进。
(1) 就CGE模型的变量设定而言, 由于国内的能源价格受到各种因素的影响, 其波动具有一定的随机性, 故前期的研究难以反映出实际的经济运行情况。目前国内终端能源价格始终受到一定程度的国家管制, 但随着能源价格市场化改革的深入, 能源价格的市场化将成为未来的发展趋势。因此, 本文假定中国工业行业消费的能源价格外生是合理的, 但将进一步测算当前国内终端能源价格与国际终端能源价格的扭曲程度, 以探索在中国能源价格市场化的情境下, 能源价格扭曲消失后可能对中国各类工业行业出口的影响。
(2) 从出口贸易结构的视角来看, 前期研究主要是从出口商品的类别结构出发, 对各类商品出口如何应对能源价格变化提出了政策建议。本文研究的是能源价格对不同工业行业出口的影响, 从能耗角度来划分出口结构将更加合理和科学。将出口工业行业划分为高、低能耗工业行业两个类别, 进而模拟能源价格市场化改革后不同情境下能源价格波动对高、低能耗工业行业出口的影响。
(3) 前期的研究中针对不同技术进步水平下, 能源价格对出口贸易的影响分析相对较少。由于技术进步在特定的情况下可作为外生力量, 对经济的整体运行和发展产生一定的影响, 因此本文将设置现有技术水平和较高技术进步水平两种情境, 来探讨能源价格市场化后对中国高、低能耗工业行业出口的影响。
2 中国工业行业能耗密度划分与能源价格扭曲测算
2.1 中国高、低能耗工业行业划分
《中国能源统计年鉴》将中国各行业的能源消耗分类为47个行业, 世界投入产出数据库2016年发布的“投入产出表(中国)”涉及56个行业, 中国国家统计局公布的《中国投入产出表》涉及42个行业。基于以上3种分类, 对中国各行业的分类进行交叉比对和归类, 可分为19类, 如表 1所示。
表 1
中国各行业分类
| 编号 | 行业 |
| 1 | 农林牧渔业 |
| 2 | 采矿采石业 |
| 3 | 食品和烟草制造业 |
| 4 | 纺织品、服饰制造业 |
| 5 | 木材制造、家具制造及其他制造业 |
| 6 | 造纸、印刷和出版业 |
| 7 | 化学工业 |
| 8 | 非金属矿物制品业 |
| 9 | 金属原料和合金制品制造业(机械设备除外) |
| 10 | 通信设备、计算机及其他电子设备制造业 |
| 11 | 机械设备制造与维护修理安装业 |
| 12 | 交通运输设备制造业 |
| 13 | 电力、热力和燃气的生产和供应业 |
| 14 | 焦炭和精炼石油制品制造业 |
| 15 | 水的生产和供应 |
| 16 | 建筑业 |
| 17 | 批发零售和住宿餐饮业 |
| 18 | 交通运输和仓储邮政业 |
| 19 | 其他第三产业 |
各类商品的最终能源消耗包括生产过程中直接的能源消耗和中间投入品间接的能源消耗。基于世界投入产出数据库的“投入产出表(中国)”与《中国能源统计年鉴》中的“中国能源平衡表”及“工业分行业终端能源消费量表”, 测算2000—2014年19个行业的最终能源消费, 再依据各行业产值计算行业能耗密度。鉴于文章篇幅限制, 具体计算结果在正文中未显示。
由于本文旨在考查能源价格扭曲消除后对高、低能耗工业行业出口的影响, 因此在“社会核算表(2012年)”中, 将行业分类为高能耗工业行业、低能耗工业行业、能源行业(行业13和行业14), 以及其他行业(行业1、行业15~19)。涉及的工业行业为行业2~12, 依据历年平均能耗, 将排在平均能耗中位数之前的归类为高能耗行业(即行业2、行业7~9), 主要包括采矿、化工及金属与非金属制造业等, 排在中位数之后的归类为低能耗行业(即行业3~6和行业10~12), 主要包括机械和设备制造业、食品及各类生活消费品制造业。
2.2 能源价格扭曲测算
CHAI J等人[9]和JU K等人[10]将能源价格扭曲的测算方法分为价格绝对扭曲程度、价格相对扭曲程度和价格动态扭曲程度3类。由于国内外能源价格的形成机制和税赋水平并不相同, 因此国内外的能源绝对价格差异终将存在。本文拟测算能源价格扭曲是基于当前中国能源价格面临持续的市场化改革, 国内外能源价格的波动势必将趋于一致的现实基础。在这样的背景下, 测算能源价格相对扭曲与能源价格动态扭曲更具现实意义。
本文借鉴上述思想, 从能源价格扭曲程度出发, 改进测算方法。鉴于数据来源的限制, 以及美国能源终端市场最接近完全自由竞争市场, 因此选用美国能源价格替代国际能源价格, 作为中国能源价格扭曲程度测算的参照价格。假定涉及的两个能源行业生产相对应的两类能源商品, 这两类能源商品的国内价格来源于历年的《中国统计年鉴》、国外能源价格依据美国能源信息管理局发布的相关数据, 并根据中国各类能源消费占比加权计算而得。
2.2.1 能源价格静态相对扭曲程度测算
能源价格相对扭曲实际上是测算两国间两类不同能源价格的相对波动程度。本文以焦炭和精炼石油制品的综合价格为参照物, 中美两国这类能源的综合价格分别为P1c和P1a, 两国电力、热力和燃气供应业综合价格分别为P2c和P2a。两国两类能源的价格之比分别为P2c/P1c和P2a/P1a, 中国电力、热力和燃气的综合价格相对于美国同类能源价格的相对扭曲程度为
| $ R_{\mathrm{ca}}=\frac{\frac{P_{2 \mathrm{c}}}{P_{1 \mathrm{c}}}}{\frac{P_{2 \mathrm{a}}}{P_{1 \mathrm{a}}}} $ | (1) |
可以看出, 式(1)的计算结果始终为正。如果计算值大于1, 则说明中国电力、热力和燃气价格与焦炭和精炼石油制品的波动相比美国同类能源的波动更大; 反之, 则波动更小。
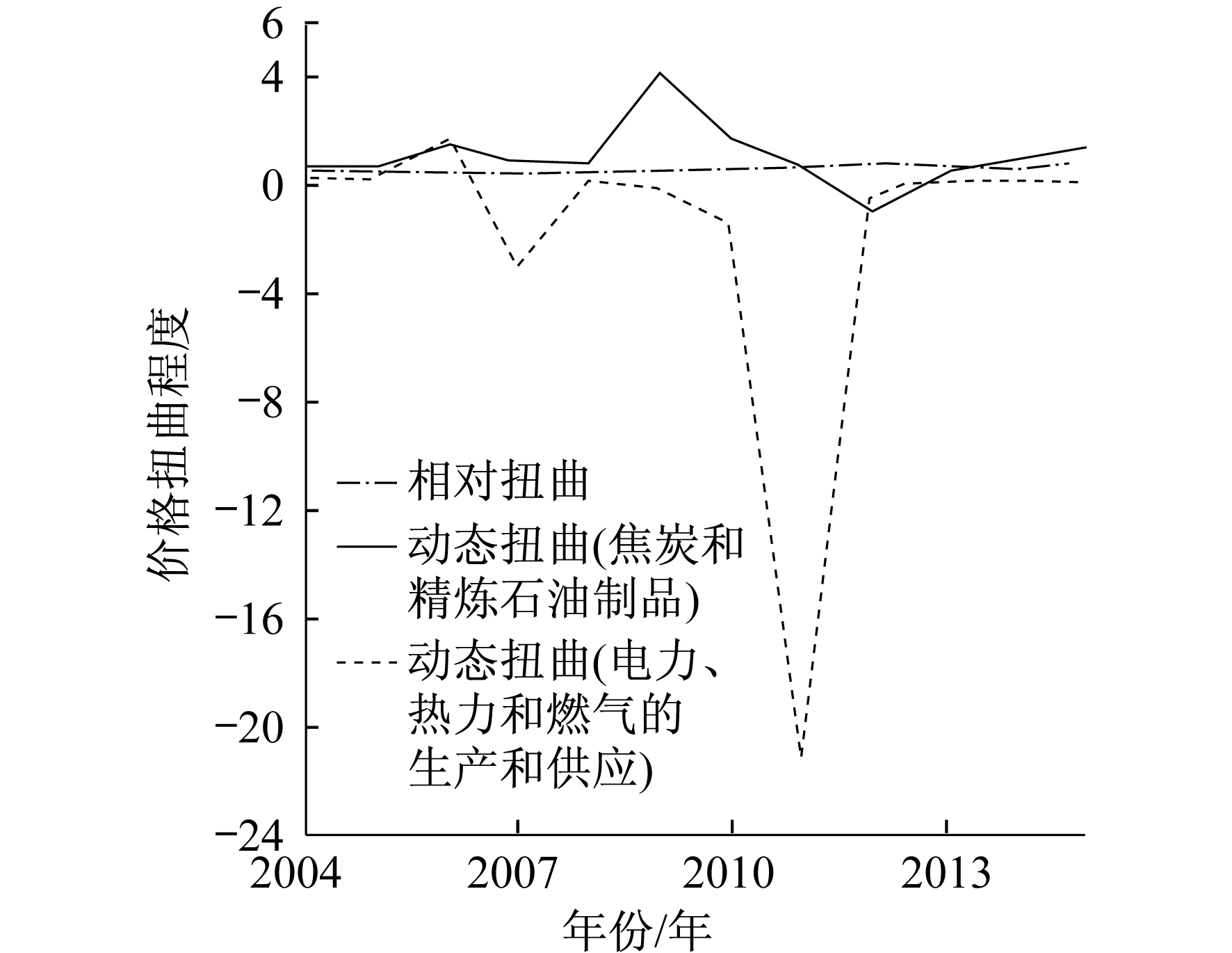
2004—2015年间中国能源价格扭曲程度的计算结果如图 1所示。由图 1可以看出, 相对扭曲程度始终小于1, 且曲线较为平稳。这说明与美国同类能源相比, 中国电力、热力和燃气能源产品的价格波动幅度较焦炭和精炼石油制品类能源价格波动程度更小, 且波动程度差距较稳定。
2.2.2 能源价格的动态扭曲程度
能源价格动态扭曲是测算两国间同类能源较上期波动的差异程度。假设中国能源在t时期综合价格为Pt, c, 在t+1时期价格为Pt+1, c, 美国相对应的价格为Pt, a和Pt+1, a, 两国能源综合价格在两个时期的比值为Pt+1, c/Pt, c和Pt+1, a/Pt, a, 因此中美两国能源综合价格的动态扭曲程度为
| $ M_{\mathrm{ca}}=\frac{\frac{P_{t+1, \mathrm{c}}}{P_{t, \mathrm{c}}}}{\frac{P_{t+1, \mathrm{a}}}{P_{t, \mathrm{a}}}} $ | (2) |
可以看出, 若式(2)计算结果的绝对值大于1, 说明中国该类能源的价格波动较美国同类能源更大; 反之, 则较美国小; 计算值如果为正, 说明中国能源价格与美国同类能源的价格波动方向一致; 反之, 则波动方向相反。由图 1可以看出, 中美焦炭和精炼石油制品价格的动态扭曲程度仅在2006年、2009年、2010年、2015年这4年中绝对值大于1, 意味着这4年中国的焦炭和精炼石油制品价格较上年的波动幅度比美国大, 其余年份均比美国小; 而中美电力、热力和燃气能源价格的动态扭曲程度则仅在2006年、2007年、2011年这3年中绝对值大于1, 其余年份值年均较小(小于0.3)。同时, 中美焦炭和精炼石油制品价格扭曲程度仅2012年为负; 而电力、热力和煤气价格的扭曲程度则在2007年和2009—2012年共5年为负。这说明在大多数年份中, 中国能源价格的波动不论上涨或下跌均小于美国能源价格的波动程度; 而少数年份中比值的绝对值大于1, 这体现了能源价格波动调整的滞后性。同时, 中国焦炭和精炼石油制品的价格波动趋势与美国同类产品的一致性程度较电力、热力和燃气能源产品要高。
上述分析结论与现实相吻合, 这是因为中国焦炭和精炼石油制品价格的市场化程度较电力、热力和燃气等能源产品高。以成品油与电力这两类能源产品为例, 在调价周期方面, 成品油的调价周期只有10个工作日, 而煤电联动的周期不少于6个月, 煤电联动尚未形成有效机制, 不能像成品油价一样较好地反映国际油价的变动趋势。在价格形成机制方面, 成品油价格在竞争性领域和环节已基本放开, 而电力价格在上网环节、输配电及销售环节, 政府定价仍占据主导地位, 市场化程度较低。因此, 电力价格的波动幅度更小, 波动趋势更为独立。
3 能源价格外生的出口贸易CGE模型构建
3.1 能源价格波动与出口贸易的相互作用机制及CGE模型的构建
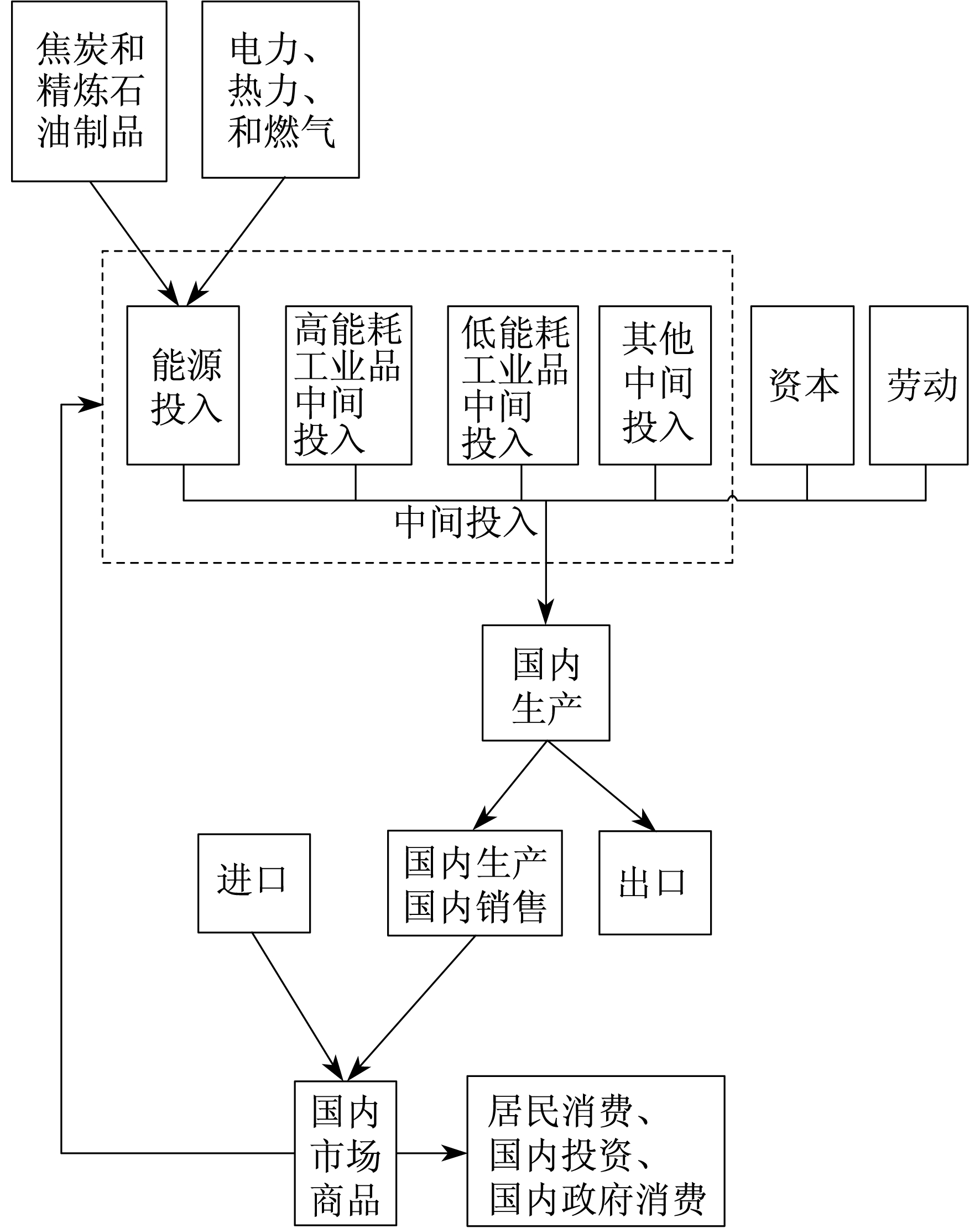
从理论上讲, 能源价格通过将能源作为中间投入直接影响到国内商品的生产成本, 从而影响商品出口的价格竞争力。其影响机制是通过成本机制, 在消费者市场自由选择的综合作用下影响出口贸易。图 2描述了能源价格和出口贸易的关系。
由图 2可以看出, 本文构建了一个由2个工业部门、2个能源部门、1个其他部门组成的CGE静态模型。在模型结构上, CGE模型包含生产、需求、贸易、分配和均衡5个模块, 涉及35个方程组。因篇幅限制, 下文仅简要介绍模型结构特点、主要假设及核心方程。设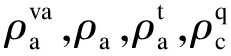 为增加值、国内产出、国内产出分配与国内市场产品构成的生产函数参数。
为增加值、国内产出、国内产出分配与国内市场产品构成的生产函数参数。
各部门投入的增加值为
| ${Q_{{\rm{VA\_a}}}} = a_{\rm{a}}^{{\rm{va}}}{[\delta _{{\rm{1a}}}^{{\rm{va}}}Q_{{\rm{LD\_a}}}^{\rho _{\rm{a}}^{{\rm{va}}}} + (1 - \delta _{{\rm{1a}}}^{{\rm{va}}})Q_{{\rm{KD\_a}}}^{\rho _{\rm{a}}^{{\rm{va}}}}]^{\frac{1}{{\rho _{\rm{a}}^{{\rm{va}}}}}}}$ | (3) |
各部门总产出为
| $ {Q_{{\rm{A\_a}}}} = a_{\rm{a}}^{\rm{q}}{[\delta _{\rm{a}}^{\rm{q}}Q_{{\rm{VA\_a}}}^{{\rho _{\rm{a}}}} + (1 - \delta _{\rm{a}}^{\rm{q}})Q_{{\rm{INTA\_a}}}^{{\rho _{\rm{a}}}}]^{\frac{1}{{{\rho _{\rm{a}}}}}}}$ | (4) |
式中:QVA——增加值;
_a——所有部门;
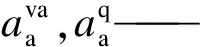 增加值与国内产出的常替代弹性函数参数;
增加值与国内产出的常替代弹性函数参数;
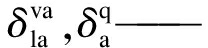 增加值与国内产出的常替代弹性函数份额参数;
增加值与国内产出的常替代弹性函数份额参数;
QLD, QKD——劳动与资本生产要素;
QA——国内总产出;
QINTA——中间投入。
各部门要素投入的最优条件为
| $ \frac{W_{\mathrm{L}}\left(1+t_{\mathrm{val}}\right)}{W_{\mathrm{K}}\left(1+t_{\mathrm{vak}}\right)}=\frac{\delta_{\mathrm{la}}^{\mathrm{va}}}{1-\delta_{\mathrm{la}}^{\mathrm{va}}}\left(\frac{Q_{\mathrm{KD}_{-\mathrm{a}}}}{Q_{\mathrm{LD}_{\mathrm{a}}}}\right)^{1-\rho_{\mathrm{a}}} $ | (5) |
式中:WL, WK——劳动与资本价格;
tval, tvak——劳动与资本增值税率。
各部门投入的最优条件为
| $\frac{P_{\mathrm{VA}_{-} \mathrm{a}}}{P_{\mathrm{INTA}_{-} \mathrm{a}}}=\frac{\delta_{\mathrm{a}}^{\mathrm{q}}}{1-\delta_{\mathrm{a}}^{\mathrm{q}}}\left(\frac{Q_{\mathrm{INTA}_{-} \mathrm{a}}}{Q_{\mathrm{VA_{-} \mathrm{a}}}}\right)^{1-\rho_{\mathrm{a}}}$ | (6) |
式中:PVA——增值部分汇总价格;
PINTA——中间投入总价格。
国内产出分配为
| $ {Q_{{\rm{A\_a}}}} = a_{\rm{a}}^{\rm{t}}{[\delta _{\rm{a}}^{\rm{t}}Q_{{\rm{VA\_a}}}^{\rho _{\rm{a}}^{\rm{t}}} + (1 - \delta _{\rm{a}}^{\rm{t}})Q_{{\rm{E\_a}}}^{\rho _{\rm{a}}^{\rm{t}}}]^{\frac{1}{{\rho _{\rm{a}}^{\rm{t}}}}}} $ | (7) |
式中:
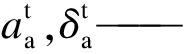 常转换弹性函数参数与函数份额参数;
常转换弹性函数参数与函数份额参数;
QE——商品出口数量。
国内产出分配优化条件1为
| $ \frac{P_{{{\rm{DA\_a}}}}}{P_{{{\rm{E\_a}}}}}=\frac{\delta_{\mathrm{a}}^{\mathrm{t}}}{1-\delta_{\mathrm{a}}^{\mathrm{t}}}\left(\frac{Q_{{{\rm{E\_a}}}}}{Q_{{{\rm{DA\_a}}}}}\right)^{1-\rho_{\mathrm{a}}^{\mathrm{t}}} $ | (8) |
式中:PDA——国产内销价格;
PE——出口商品价格;
QDA——国内生产国内使用数量。
国内产出分配优化条件2为
| $P_{\mathrm{B}}(b) Q_{\mathrm{B}}(b)=P_{\mathrm{DB}}(b) Q_{\mathrm{DB}}(b)+P_{\mathrm{EB}}(b) Q_{\mathrm{EB}}(b)$ | (9) |
式中:b——除能源部门外的部门;
PB——b部门国内生产活动价格;
QB——b部门总产出;
PDB——b部门国家内销的价格;
QDB——b部门国内生产国内使用活动的数量;
PEB——b部门国内生产商品的出口价格;
QEB——b部门出口数量。
国内市场产品的构成为
| $ {Q_{{\rm{Q\_c}}}} = a_{\rm{c}}^{\rm{q}}{[\delta _{\rm{c}}^{\rm{q}}Q_{{\rm{DC\_a}}}^{\rho _{\rm{c}}^{\rm{q}}} + (1 - \delta _{\rm{c}}^{\rm{q}})Q_{{\rm{M\_c}}}^{\rho _{\rm{c}}^{\rm{q}}}]^{\frac{1}{{\rho _{\rm{c}}^{\rm{q}}}}}}$ | (10) |
式中:_c——所有产品;
QQ——国内市场供应商品;
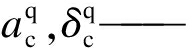 QQ的阿明顿函数参数与份额参数;
QQ的阿明顿函数参数与份额参数;
QDC——国产内销产品数量;
QM——进口商品数量。
国内市场产品构成优化条件为
| $ \frac{P_{\mathrm{DC}_{-} \mathrm{c}}}{P_{\mathrm{M}_{-} \mathrm{c}}}=\frac{\delta_{\mathrm{c}}^{\mathrm{q}}}{1-\delta_{\mathrm{c}}^{\mathrm{q}}}\left(\frac{Q_{\mathrm{M}_{-} \mathrm{c}}}{Q_{\mathrm{DC}_{-} \mathrm{c}}}\right)^{1-\rho_{\mathrm{c}}^{\mathrm{q}}} $ | (11) |
式中:PDC——国产内销价格;
PM——进口价格;
QM——进口数量。
出口方程为
| $ Q_{\mathrm{E}_{-} \mathrm{c}}=\kappa P_{\mathrm{WE}_{-\mathrm{c}}}^{-\beta_{\mathrm{c}}} p_{\mathrm{w_{-}c}}^{\beta_{\mathrm{c}}-1} Y^{\phi_{\mathrm{c}}} $ | (12) |
式中:QE——出口数量;
κ——出口金额;
PWE——离岸价格;
βc——出口需求弹性;
pw——国际市场价格;
Y——影响出口的GDP指数;
φc——出口收入弹性。
影响出口GDP价格指数为
| $ Y=\frac{\sum\limits_{i} G_{\mathrm{DP}}\left(1+R_{\mathrm{GDP}_{i, j}}\right)}{\sum\limits_{i} G_{\mathrm{DP}_{i, j-1}}} $ | (13) |
式中:i——出口贸易伙伴国;
j——年份;
GDP——国内生产总值;
RGDP——GDP增长率。
出口产品价格为
| ${P_{{\rm{E\_c}}}} = {P_{{\rm{WE\_c}}}}(1 - {t_{{\rm{x - c}}}}){E_{\rm{X}}}$ | (14) |
式中:tx——出口关税税率;
EX——汇率。
(1) 生产模块 各部门产出采用由中间产品和要素投入带来的增加值所组成的嵌套常替代弹性生产函数表示。其中, 中间产品分类为能源产品、低能耗工业品、高能耗工业品与其他中间投入, 要素投入只考虑劳动力和资本。假设以生产成本最小化为目标, 能源价格为外生变量, 其余中间产品、要素投入需求和价格均为内生变量, 公式如式(3)~式(6)。
(2) 需求模块 最终产品需求包括居民消费、政府消费、投资需求和出口需求。其中, 居民消费是内生的, 由可支配收入约束下的斯通-杰瑞效用最大化函数来描述, 且假设边际消费倾向不变。政府支出是外生变量, 投资需求包括固定资产和存货增加。
(3) 贸易与价格模块 对外贸易中, 商品涉及国内生产出口部分、国内生产国内使用部分、进口商品国内使用部分。生产者将可贸易产品在出口和国内销售之间进行最优组合, 以实现总产出分配利润最大化, 由常转换弹性函数来描述, 如式(7)~式(9)。式(9)在已知汇率和市场出口价格的情形下, 出口商品价格是确定的, 从国内生产活动价格即可推导出国内生产国内使用该商品的价格, 而文中模型假定能源类商品国内生产国内使用价格为外生变量, 因此式(9)中的商品类别不涵盖能源类商品。基于阿明顿假设, 消费者购买商品时, 将国内市场供给中国内生产国内使用部分与进口商品国内使用部分进行最优组合, 通常利用常替代弹性函数进行描述, 如式(10)和式(11)。为充分反映现实, 进口产品遵循“小国假设”, 采用出口方程描述中国产品出口数量与国际市场价格和进口国收入之间的关系[12]。其中, 出口价格由内生的国内产出和国际进口需求及外生的关税和汇率共同决定。通过设置国外GDP指数这一变量来反映进口经济收入水平的变化对中国出口的影响, 如式(12)~式(14)。这种假设体现了中国作为世界最大出口国, 其出口贸易的变化将影响市场供给, 但仍难以取得对进口产品的国际市场定价权。
(4) 分配模块 政府向居民和企业征税, 并将税收用于消费支出、储蓄和转移支付。除了储蓄以外, 企业和居民之间也存在收入转移支付, 将外汇收支的差额作为国外储蓄, 其为内生变量。
(5) 均衡模块 遵循凯恩斯闭合的基本原则, 将劳动力价格和名义汇率设定为外生变量, 政府消费总额和投资是由外生变量所决定的, 劳动力数量和经常账户余额设定为内生变量。模型均衡条件涉及产品市场均衡、要素市场均衡、储蓄与投资均衡、政府收支平衡与国外收支平衡5个方面。
3.2 社会核算矩阵的构建与数据来源
以上模型计算的实现均是基于“中国社会核算表(2012年)”。本文以中国2012年42个部门的“投入产出表”为基础, 将42个部门整理合并成5个部门, 分别为高能耗工业制品行业, 低能耗工业制品行业, 焦炭和精炼石油制品制造业, 电力、热力和燃气的生产和供应业, 以及其他行业。假设每个活动只生产单一商品, 则商品账户与活动账户相同。
要素账户包括资本账户与劳动账户。机构账户包括家庭账户、企业账户和政府。由于本文旨在模拟能源价格市场化后对出口的影响, 所以对家庭和企业不再进一步细分。构建中国能源价格的“社会核算表(2012年)”的数据来源于《中国2012年投入产出表》《中国统计年鉴》《中国财政年鉴》。
当经济达到均衡时, 社会核算矩阵中任意部门的支出列总和与收入的行总和应该相等。但由于编制社会核算表时的数据来源不同, 使得各部门的列总和与收入的行总和并不相等, 需要调整社会核算矩阵。本文采用双边比例法对“社会核算表”进行调整。
4 中国能源价格市场化对高、低能耗工业行业出口的影响分析
本文的分析是以美国作为能源价格市场化的参考国, 假设中国能源价格市场化后, 中国历年能源价格的波动程度应与美国相同。结合研究目标, 首先假设两种不同情境, 并将能源价格市场化后的波动数据纳入CGE模型进行分析, 具体影响结果如表 2所示。
表 2
情境1和情境2下能源价格市场化前后的高、低能耗工业品出口价格影响
| 情境 | 工业品类别 | 市场化前 | 市场化后 | 变化率/ % |
| 千万元 | ||||
| 1 | 高能耗 | 174 153 | 169 409 | -2.72 |
| 低能耗 | 877 856 | 864 917 | -1.47 | |
| 2 | 高能耗 | 174 153 | 178 406 | 2.44 |
| 低能耗 | 877 856 | 889 734 | 1.35 |
|
情境1 现有技术水平条件下, 在能源价格相对扭曲消除后, 即中国电力、热力和燃气价格相较于炼焦、精炼石油制品价格的波动与美国同类能源商品价格的波动程度相同, 2012年中国电力、热力和燃气价格应在原有价格基础上向上波动18.1%。
情境2 现有技术水平条件下, 在能源价格动态扭曲消除后, 即中国电力、热力和燃气价格相较于炼焦、精炼石油制品价格的波动程度与美国同类商品相同, 2012年中国石油、炼焦与电力、热力和燃气的价格分别较原有价格下跌3.41%和13.59%。
在CGE模型中, 生产函数假定为CES生产函数, 如式(4)。商品的生产效率由生产资本-劳动替代弹性ε=1/(1-ρa)决定。由于本文的分析中, 将技术进步视为外生变量, 考虑到能源价格与生产活动中节能技术进步之间的内生关系, 所以这一设定具有一定的局限性。因此, 文中为了考察更高的技术进步水平下, 能源价格市场化对中国不同能耗工业行业出口的影响, 做了如下假定。
情境3 为便于测量, 假定中国的未来技术水平与美国相当, 参照文献[13-14]对美国常替代弹性生产函数(资本-劳动替代弹性)的计算结果, 设定中国资本-劳动替代弹性, 同时能源价格变动保持与情境1相同。
情境4 技术进步的幅度与情境3中的假设相同, 能源价格变动与情境2的假设相同。
按照以上两种不同假设前提, 进一步运用GAMS软件模拟能源价格变动对中国高、低能耗工业行业出口的影响, 具体影响结果如表 3所示。
表 3
情境3和情境4下能源价格市场化前后的高、低能耗工业品出口价格影响
| 情境 | 工业品类别 | 市场化前 | 市场化后 | 变化率/ % |
| 千万元 | ||||
| 3 | 高能耗 | 174 153 | 171 416 | -1.57 |
| 低能耗 | 877 856 | 869 420 | -0.96 | |
| 4 | 高能耗 | 174 153 | 176 528 | 1.36 |
| 低能耗 | 877 856 | 885 344 | 0.85 |
|
由上述模拟结果可以发现, 假定中国能源价格市场化后, 能源价格无论是向上还是向下波动, 幅度都有可能加剧。无论是在现有技术水平下, 还是在高技术进步水平下, 能源价格向上波动都将会导致中国的工业品出口整体减少, 其中对于高能耗工业行业出口的抑制影响程度要远大于低能耗工业行业。相反, 无论是在现有技术水平下, 还是在高技术进步水平下, 能源价格向下波动都将会导致中国的工业品整体出口增长, 其中对于高能耗工业行业出口的推动影响程度要远大于低能耗工业行业。
对比情境1和情境3中不同能耗工业行业出口下降的幅度, 发现情境3中高能耗工业行业出口变化率为情境1的57.7%, 低能耗工业行业在情境3中的变化率为情境1的65.3%。这说明技术进步后, 能源价格向上波动相同幅度时, 高能耗工业行业出口的规模较现有技术水平下减少的幅度要小, 且减少的幅度小于低能耗工业行业。对比情境2和情境4, 可以发现类似结论, 即处于高技术进步水平下, 能源价格向下波动时, 高能耗工业行业的出口规模较现有技术水平下增加的幅度要小, 且增幅也小于低能耗工业行业。这意味着若整体经济发展处于较高的技术进步水平下, 那么能源价格市场化波动对高低能耗工业行业出口的冲击幅度相对于低技术水平下都将较小。
5 政策建议
为了保障中国出口贸易的稳定持续发展, 继续发挥出口贸易对中国经济增长的拉动作用, 以下分别从优化不同能耗出口行业结构的角度和提升出口能耗处理技术水平两方面提出政策建议。
首先, 在能源价格机制改革方面, 应当坚持谨慎渐进的原则, 按照能源品种进行价格市场化, 同时根据能源品种消费的比例, 对其中重点能源品种的价格机制改革的推进应该基于经济基本面稳定这一大前提下进行, 改革的步伐宜缓不宜急, 给予出口贸易更多的反应和调整的时间。而与此同时, 中国对于整体出口贸易的发展战略应该有所改变, 降低对低价格能源要素的依赖, 从多方面、多角度构建新出口的贸易竞争优势点。
其次, 在出口贸易行业结构方面, 为顺应当前供给侧改革, 政府应推行合理产业政策, 对于低能耗工业行业出口可以用财政政策给予适当的激励。对于部分依赖高能耗取得出口优势的企业, 政府应敦促、鼓励企业从生产、创新等角度出发, 改变不同能耗行业的生产结构, 从而减少对高能耗工业行业出口的依赖。这样在未来能源价格市场化后, 一方面可以提升中国能源资源的使用效率, 另一方面可以降低能源价格剧烈波动对整体出口贸易的负面影响。
最后, 在高技术进步水平下, 使能源价格波动对出口的影响冲击较小。政府应鼓励创新, 推动整体经济的技术创新。另外, 政府应切实采取各种政策扶持和鼓励企业加大技术研发力度, 提升能耗处理技术水平, 以提高能源使用效率。尤其是在能源价格上涨的情况下, 引导企业节能技术水平的提升可以有效地减少中国高、低能耗行业出口对能源要素价格优势的依赖, 从而避免能源价格市场化后能源价格波动对出口贸易产生的冲击。
6 结语
现阶段中国能源价格市场化的深化改革趋势已经形成, 未来能源价格的走势将对出口贸易产生影响, 尤其是对不同能耗的工业行业会有一定的差异化影响。本文的研究结论表明, 中国能源价格市场化后, 无论是价格上涨或下跌, 能源价格波动幅度在很大概率上都将扩大化, 相较于低能耗工业行业的出口, 能源价格的剧烈波动对高能耗工业行业出口的影响将更为明显。为实现中国出口贸易的平稳可持续发展, 必须对能源价格机制改革的节奏有所把控, 同时采取必要的出口贸易政策对不同能耗工业行业进行调控, 加强技术投入, 为改革提供更好的条件。
参考文献
-
[1]国内外能源相对价格、技术进步与出口规模增长[J]. 世界经济研究, 2010(10): 41-45.
-
[2]全面推进能源价格市场化[J]. 价格理论与实践, 2017(12): 17-22.
-
[3]能源约束对出口贸易结构影响的实证分析[J]. 国际商务(对外经济贸易大学学报), 2009(3): 10-15.
-
[4]要素价格与中国产业国际竞争力:基于ISIC的跨国比较[J]. 统计研究, 2010(8): 56-65. DOI:10.3969/j.issn.1002-4565.2010.08.008
-
[5]ABIMANYU Y. Oil price, government revenue, export value, and economic growth: Indonesia's case[J]. Kajian Ekonomi and Keuangan, 2016, 20(3): 214-230.
-
[6]能源要素价格改革对我国经济发展的影响分析——基于一个动态可计算一般均衡(CGE)模型[J]. 系统工程, 2009(2): 91-95.
-
[7]LEVENT A, MUSTAFA A. Economic impact of oil price shocks on the Turkish economy in the coming decades: a dynamic CGE analysis[J]. Energy Policy, 2011, 39(3): 1722-1731. DOI:10.1016/j.enpol.2010.12.051
-
[8]高志远.基于CGE模型的能源价格波动对国民经济影响研究[D].北京: 中国矿业大学, 2015.
-
[9]CHAI J, GUO J E, WANG S Y, et al. Why does energy intensity fluctuate in China?[J]. Energy Policy, 2009, 37(12): 5717-5731. DOI:10.1016/j.enpol.2009.08.037
-
[10]JU K, SU B, ZHOU D Q, et al. Does energy-price regulation benefit China's economy and environment? Evidence from energy-price distortions[J]. Energy Policy, 2017(2): 108-119.
-
[11]ZHAI F, HERTEL T. Impacts of the Doha development agenda on China: the role of labor markets and complementary education reforms[J]. Policy Research Working Paper, 2005(22): 7727-7737.
-
[12]中国出口增长的就业效应:基于CGE模型的分析[J]. 国际贸易问题, 2011(9): 14-24.
-
[13]YUHN K. Economic growth, technical change biases, and the elasticity of substitution: a test of the de La Grandville hypothesis[J]. The Review of Economics and Statistics, 1991, 73(2): 340-346. DOI:10.2307/2109526
-
[14]KLUMP R, MCADAM P, WILLMAN A. Factor substitution and factor-augmenting technical progress in the united states: a normalized supply-side system approach[J]. The Review of Economics and Statistics, 2007, 89(1): 183-192. DOI:10.1162/rest.89.1.183