视觉目标跟踪是计算机视觉领域一个重要的研究方向。随着计算机计算能力的提升、摄像设备的普及和数据存储成本的下降, 视觉目标跟踪广泛应用于移动识别、智能视频监控、视频索引、人机交互、交通管理和视觉导航等领域。

基于相关滤波器的目标跟踪算法将空域中复杂的卷积运算转换到频域中完成, 时间复杂度极低, 具有很高的跟踪效率和鲁棒性, 近年来逐渐成为实现实时目标跟踪的主流技术^[1]。文献[2]在MOSSE滤波器中引入核方法, 实现了非线性分类; 文献[3]在文献[2]提出的核化相关滤波方法的基础上, 提出了多特征融合的方法, 将方向梯度特征、局部二值模式特征和灰度特征进行融合, 形成了新的特征表达; 文献[4]引入颜色属性值, 增强了像素的描述能力; 文献[5-6]加入尺度控制, 提高了算法对目标尺度变化的鲁棒性; 文献[7-9]引入深度学习, 对深度学习特征做相关滤波, 将特征从人工选定特征扩充到了深度学习特征; 文献[10]采用连续滤波器进行目标跟踪; 文献[11]针对文献[10]存在的过拟合和采样存储问题, 使用少量的滤波器参数替代原来大量的过滤器参数, 并结合高斯混合模型减少了存储的样本数量, 保持了样本的差异性; 文献[12]在文献[11]的基础上引入了稳定性概念, 对滤波器的每一部分引入一个权值, 由此决定是否使用其进行跟踪, 通过构造一个滤波器大小相同的矩阵, 在使用滤波器前与之相乘, 最终使得滤波器不可靠部分数值较小, 从而提升了跟踪精度。上述研究关注了特征模型的改进及对尺度变换的支持, 提高了相关滤波跟踪的性能, 然而在模板的更新策略上, 一般采用简单的插值方法实现对模板的在线学习^{[2, 10]}, 当视频中出现长期的目标遮挡、目标消失或因为检测错误而出现目标漂移时, 很难从跟踪错误中恢复。

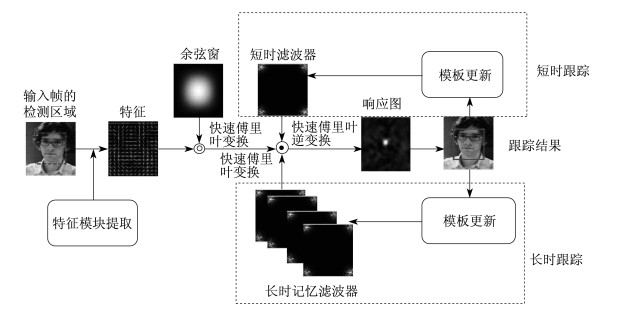
本文使用ASMM(Atkinson - Shiffrin Memory Model)^[13]记忆模型, 设计了更符合人的视觉跟踪的更新策略, 并将此策略应用于核化相关滤波器, 提出了基于记忆模型的核化相关滤波目标跟踪算法。该算法参照ASMM记忆模型设计了适合目标跟踪的记忆机制, 将标准模板分为短时记忆模板和长时记忆模板库, 模板库的更新遵循记忆模型。将目标跟踪过程分为短时跟踪和长时跟踪:短时跟踪在视频的每一帧上进行, 调用的是短时记忆模板; 长时跟踪在固定的时间间隔内发生, 调用的是长时记忆模板库, 可以修正短时跟踪的错误。实验结果表明, 该目标跟踪框架是可行的, 目标跟踪算法能够实现对跟踪错误的恢复。

ASMM记忆模型描述了人记忆的基本结构和原理。在ASMM记忆模型中, 人的记忆由3个阶段组成:感官记忆、短时记忆和长时记忆。在感官记忆阶段, 环境信号传入感觉注册机, 转化成化学和物理信号, 用于生物系统的处理, 形成视觉信号、听觉信号和感觉信号等。这些信号经过回想、编码、决策、检索等一系列信息处理过程, 得到短时记忆。短时记忆经过不断的记忆、遗忘和响应输出的反馈, 变成长时记忆。

参考ASMM记忆模型, 本文建立了目标跟踪的特征记忆机制, 将记忆分为短时记忆和长时记忆, 并据此把目标跟踪过程分为短时跟踪和长时跟踪两个部分。短时跟踪根据短时记忆快速进行粗略的目标跟踪; 长时跟踪在固定的时间间隔内, 根据长时记忆库做精确跟踪, 以更正短时跟踪的错误, 获得更高的跟踪性能。

设计特征记忆库M, 记忆库包含两种记忆类型——短时记忆记为S, 长时记忆记为L, 则M = S ∪ L。对于L中的每个模板${\mathit{\boldsymbol{\hat x}}_i}$和相应的滤波器参数${\mathit{\boldsymbol{\widehat a}}_i}$ (i=1, 2, 3, …, N, N为长时记忆的最大容量), 定义记忆向量(τ_i, h_i), 其中τ_i表示每个样本的记忆时间, h_i表示每个样本的记忆强度。

短时跟踪时, 跟踪器得到响应值最高的待选目标框, 记忆机记忆待选目标框的特征为模板和更新滤波器, 并存储为短时瞬间记忆, 同时当响应值大于阈值t_h时, 认为该模板是稳定的且对目标有较强的表示能力的模板, 把新的模板$ \mathit{\boldsymbol{\widehat x}}$和滤波器$\mathit{\boldsymbol{\widehat a}}$加入到长时记忆库中, 并初始化记忆变量(τ, h)。短时记忆保留时间较短, 仅通过插值的方式保留到下一帧; 长时记忆用记忆库保存, 保留时间较长。

使用短时记忆和长时记忆库记载的模板和滤波器进行跟踪, 即是对记忆的回想、检索、决策和反馈阶段。在短时跟踪时, 基于时间的连续性, 回想调用短时记忆, 决策输出响应值最高的坐标为目标中心位置。在长时跟踪时, 需要“仔细”识别, 调用长时记忆库来进行识别, 回想并检索所有长时记忆, 用所有的模板和滤波器计算最大响应值, 取获得最高响应值的模板和滤波器为当前模板和滤波器, 并反馈响应信息给此模板和滤波器, 把它们的记忆强度值增加1, 同时更新目标的短时记忆和长时记忆。

长时记忆库的容量是有限的, 当容量超过最大限度时, 部分记忆会被遗忘, 记忆的遗忘遵循遗忘曲线规律^[14]。模板和滤波器的记忆能力记为$r$, 由遗忘曲线规律得到$ r$和记忆时间$ \tau $与强度$ h$的关系, 即

$ r = {\rm{exp}}\left( { - \frac{\tau }{{\Gamma h}}} \right) $

(1)

式中: $\Gamma $——常量, 用来控制时间变化(timespan)的尺度。

记忆能力最弱的模板和滤波器将被遗忘, 从长时记忆库中删除。

依据设计的记忆机制, 设计新的模板更新策略。模板更新在短时跟踪阶段实现, 分别对短时记忆模板和滤波器及长时记忆模板和滤波器进行更新。

短时记忆更新的时机, 是在每一次短时跟踪之后, 根据新的目标中心位置得到模板$ \mathit{\boldsymbol{\widehat x}}$和计算出新的滤波器参数$\mathit{\boldsymbol{\widehat a}}$, 即

$ \mathit{\boldsymbol{\hat a}} = \frac{{\mathit{\boldsymbol{\hat y}}}}{{{{\mathit{\boldsymbol{\hat k}}}_t} + \mathit{\boldsymbol{\lambda }}}} $

(2)

式中: $\mathit{\boldsymbol{\widehat y}}$——核化相关滤波器的输出值;

$ {\mathit{\boldsymbol{\widehat k}}_t}$——$t $时刻核的频域值;

$\mathit{\boldsymbol{\lambda }}$——防止过度拟合的正则参数。

短时记忆模板和滤波器按简单的插值处理进行更新:

$ {\mathit{\boldsymbol{\widehat a}}_t} = \left( {1 - \eta } \right){\mathit{\boldsymbol{\widehat a}}_{t - 1}} + \eta \mathit{\boldsymbol{\widehat a}} $

(3)

$ {\mathit{\boldsymbol{\widehat x}}_t} = (1 - \mathit{\boldsymbol{\eta }}){\mathit{\boldsymbol{\widehat x}}_{t - 1}} + \mathit{\boldsymbol{\eta }}\mathit{\boldsymbol{\widehat x}}{\rm{ }} $

(4)

式中: $\mathit{\boldsymbol{\eta }}$——学习因子。

长时记忆模板和滤波器更新的时机, 是在短时跟踪中, 当响应值大于阈值时, 更新长时记忆库。先在获得最大响应值处采样得到新模板, 再按式(3)和式(4)计算新的滤波器参数, 将新的模板$\mathit{\boldsymbol{\widehat x}}{\rm{ }} $和滤波器参数$ \mathit{\boldsymbol{\widehat a}}{\rm{ }}$添加到长时记忆库中, 并对该长时记忆向量进行初始化。如果此时记忆库的容量已达到最大阈值, 则按照遗忘规则淘汰一个模板。

HOG(Histogram of Oriented Gradient)特征相对于其他人工特征, 具有图像特征信息比较全面、对几何和光学的形变都能保持良好的不变性、对光照变化和阴影都具有较好的鲁棒性等优点^[15]。因此, 本文在跟踪算法中使用HOG特征作为特征模型。

在每个Cell中将梯度细分为9个方向27个区间。其中前9个区间由[-1, 0, +1]滤波产生的结果插值得到, 第10~18个区间由[+1, 0, -1]滤波产生的结果插值得到, 第19~27个区间通过前18个区间得到。此外, 还有4个区间用来统计纹理信息。共计32个区间, 即每一个Cell最终都对应一个32维的向量特征。

由于需要做相关的滤波处理, 本文将目标框按照4×4=16的Cell尺寸划分单元, 再直接用每个Cell的梯度直方图表示每个Cell的特征。HOG特征的维数=(目标框大小÷16)×32, 取前31维向量。假设目标框大小为177×152，则HOG特征的维数为44×38×31, HOG特征设置为31个通道的特征。

本文在核化相关滤波跟踪框架^[16]的基础上, 建立了如图 1所示的基于记忆模型的核化相关滤波跟踪框架。跟踪框架由特征模型、短时跟踪、长时跟踪、模板更新等几个模块组成。输入帧的检测区域经过特征提取模块提取特征, 提取的特征乘以余弦窗以平滑边缘, 接下来的跟踪处理分为短时跟踪和长时跟踪两种类型。

基本的核化相关滤波跟踪流程包括滤波器训练和用训练好的滤波器跟踪两个部分。本文采用高斯核, 在滤波器训练时, 经文献[16]推导, 高斯核$ \mathit{\boldsymbol{k}}{^{xx\prime }} = {\rm{exp}}\left( { - \frac{1}{{{\rm{ }}{\sigma ^2}}}\left( {{{\left\| {{\rm{ }}\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{x}}{\rm{ }}\prime } \right\|}^2}} \right)} \right)$可以表示为

$ \begin{array}{l} \mathit{\boldsymbol{k}}{^{xx\prime }} = {\rm{exp}}( - \frac{1}{{{\sigma ^2}}}[{\left\| \mathit{\boldsymbol{x}} \right\|^2} + {\left\| {\mathit{\boldsymbol{x}}\prime } \right\|^2} - 2{F^{ - 1}}\cdot\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(\sum {_c\mathit{\boldsymbol{\widehat x}}* \odot } \mathit{\boldsymbol{\widehat x}}\prime )]) \end{array} $

(5)

式中: $\mathit{\boldsymbol{C}}$——多通道特征的通道数量。

记核化相关滤波器的输出值为$ {\mathit{\boldsymbol{\widehat y}}}$, 则滤波器参数$\mathit{\boldsymbol{\widehat a}} $可表示为

$ \mathit{\boldsymbol{\widehat a}} = \frac{{\mathit{\boldsymbol{\widehat y}}}}{{\mathit{\boldsymbol{\widehat k}} + \mathit{\boldsymbol{\lambda }}}} $

(6)

式中: ${\mathit{\boldsymbol{\widehat k}}}$——核的频域值;

$\mathit{\boldsymbol{\lambda }}$——防止过度拟合的参数。

目标跟踪时, 在新的一帧中用训练得到的参数$\mathit{\boldsymbol{a}}$和基采样$ \mathit{\boldsymbol{x}}$, 检测待跟踪目标区域采样, 记新的采样为$\mathit{\boldsymbol{z}}$, 则响应值$\mathit{\boldsymbol{y}}$为

$ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{C}}({\mathit{\boldsymbol{k}}^{xz}})\mathit{\boldsymbol{a}} = {\mathit{\boldsymbol{F}}^{ - 1}}({\mathit{\boldsymbol{\widehat k}}^{xz}} \odot {\mathit{\boldsymbol{\widehat a}}^)} $

(7)

式中: $\mathit{\boldsymbol{C}}$——循环采样。

$y$取最大值的坐标即为该帧估计的目标中心坐标。

对每帧图像I _t⁰(x), (t=1, 2, 3, …, m)进行短时跟踪, 采用短时记忆中的模板$\mathit{\boldsymbol{\widehat x}} $和滤波器$ \mathit{\boldsymbol{\widehat a}}$。对预估目标区域处理后的特征, 在频域和短时模板$ \mathit{\boldsymbol{\widehat x}}$、滤波器$\mathit{\boldsymbol{\widehat a}}$做快速傅里叶变换, 再做快速傅里叶逆变换回空域得到响应图, 由响应图得到跟踪结果。由跟踪结果重新采样模板、提取特征, 按照短时更新策略, 式(3)和式(4)分别更新短时模板和滤波器及长时记忆的模板和滤波器库。

用长时记忆库中保存的模板和滤波器做长时跟踪。长时跟踪时, 将待测样本和记忆库中的所有模板和滤波器做相关运算, 取得最大响应值的模板和滤波器被设为当前模板和滤波器, 同时对该模板和滤波器在记忆库中的记忆向量进行增强, 即记忆强度为h+1。

设记视频序列为I, 帧数为m, 即I ={ I _t⁰(x), t=1, 2, 3, …, m}, 每帧的跟踪结果为x_t, t=1, 2, 3, …, m。依据上述基于记忆模型的核化相关滤波跟踪流程, 建立基于记忆模型的核化相关滤波跟踪算法, 算法命名为KCF_M。KCF_M算法描述如下(在算法描述中没有设定采用的是哪种特征模型)。

输入 视频序列I ={ I _t⁰(x), t=1, 2, 3, …, m}

输出 每一帧的跟踪结果x_t, t=1, 2, 3, …, m

对第1帧图像I₁⁰(x), 以目标框中心, 按参数padding在图像上采样得$\mathit{\boldsymbol{\widehat x}}$;

以目标框中心, 计算0 - 1的高斯分布得到期望输出$\mathit{\boldsymbol{\widehat y}}$;

根据式(5)计算k ^xx′;

根据式(6)计算滤波器参数$ \mathit{\boldsymbol{\widehat a}}$, 得到样本$\mathit{\boldsymbol{\widehat x}}$和参数$ \mathit{\boldsymbol{\widehat a}}$;

对样本$\mathit{\boldsymbol{\widehat x}}$和参数$\mathit{\boldsymbol{\widehat a}}$初始化记忆向量(τ_i, h_i), 加入长时记忆库L;

for t=1 to m

  对x_t-1, 按参数padding在图像上采样得$ \mathit{\boldsymbol{\widehat z}}$;

  if mod(t, L) then //长时跟踪

   对L中的所有模板, 根据式(7)计算相应值y的集合;

   比较得到最大的响应值y_max, 其对应的记忆向量的强度值h+1;

   计算取得最大响应值的空域位置x _t;

   输出x _t;

else          //短时跟踪

   对短时记忆:样本$ \mathit{\boldsymbol{\widehat x}}$和参数$ \mathit{\boldsymbol{\widehat a}}$, 根据式(7)计算相应值y;

   比较得到最大的响应值y_max;

   计算取得最大响应值的空域位置x _t;

   输出x _t;

end if

对x _t, 按参数padding在图像上采样得$\mathit{\boldsymbol{\widehat x}}$;

根据式(5)计算k ^xx′;

根据式(6)计算滤波器参数$\mathit{\boldsymbol{\widehat a}} $, 得到样本$ \mathit{\boldsymbol{\widehat x}}$和参数$ \mathit{\boldsymbol{\widehat a}}$;

if y_max>t_h then

  对样本$\mathit{\boldsymbol{\widehat x}}$和参数$ \mathit{\boldsymbol{\widehat a}}$初始化记忆向量(τ _i, h _i);

  if长时记忆库容量 < N then

   记忆向量(τ_i, h_i)加入长时记忆库L;

else

   根据式(1)计算r, 选择r的记忆遗忘;

  end if

else

  根据式(3)和式(4)更新短时记忆样本$ \mathit{\boldsymbol{\widehat x}}$和参数$\mathit{\boldsymbol{\widehat a}}$;

end if

对L中所有记忆模板的记忆向量(τ, h)执行τ+1。

end for

从文献[17]中选取在原先的插值更新模式下出现显著跟踪错误的视频(freeman1, shaking, jogging_1, lemming, walking2, girl)进行对比实验, 采用单个视频的评估方式, 评估标准也采用中心位置误差。

跟踪算法选择HOG特征和高斯核, 高斯核的带宽因子σ设为0.5。相关滤波的空域范围参数padding设为1.5, 参数λ设为10^-4, 相关滤波器输出的空域带宽因子σ设为0.1。模板及滤波器的学习因子η设为0.02。采用记忆模型时, 长时记忆模板更新阈值t_h设为0.5, 长时记忆库的容量N设为100, 长时跟踪的时间间隔为5。

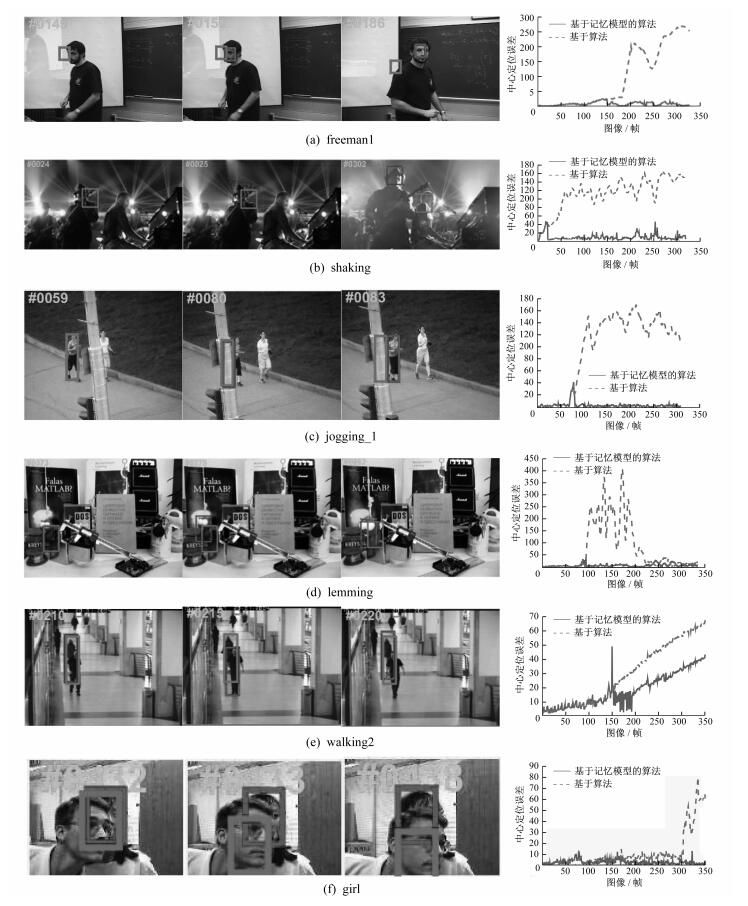
实验结果如图 2所示, 左边是关键帧, 右边是逐帧的中心误差曲线。

结合每个视频的中心误差曲线图和关键帧图对跟踪结果比较分析如下。

视频freeman1在第149帧之前发生了目标平面外旋转姿态变化, 两种算法都偏离了目标; 在第150帧, 基于记忆模型的算法在长时跟踪中借助长时记忆模板重新回到了正确位置, 而基本算法则由于没有纠错, 逐渐偏离, 直至第186帧已经完全丢失目标, 并且在后面的跟踪中一直偏离。本实例表明, 记忆模型算法纠正了由于姿态变化而发生的跟踪错误。

视频shaking在第24帧之前发生了由光照变化和动作变化而引起的目标外观变化, 两种算法都偏离了目标。在第25帧, 基于记忆模型的算法用长时记忆库的长时跟踪重新回到了正确的位置, 而基本算法则由于没有纠错, 逐渐偏离, 直至302帧已经完全丢失目标, 漂移至另一个相似目标上, 并且在余下的帧上一直偏离目标。本实例表明, 记忆模型算法纠正了由于照明和动作变化使目标外观发生变化而导致的跟踪错误。

视频jogging_1在第59帧到第80帧之间目标被遮挡, 由于时间的连续性, 两种算法都定位到了遮挡物上, 基于记忆模型算法的长时跟踪借助长时记忆模板在第83帧重新检测到目标, 而基本算法由于采用简单的插值法更新模板, 此时模板已经完全被更新成遮挡物, 因此无法再检测出目标。本实例表明, 基于记忆模型的算法可以恢复被遮挡目标的跟踪。

视频lemming在第370到373帧发生了突然移动, 到了第373帧两种算法的跟踪都有小幅度偏离, 基于记忆模型算法的长时跟踪借助长时记忆模板在第373帧矫正了目标定位, 而基本算法则在接下来的500帧内一直定位在同一个错误位置, 直到目标在第893帧在此位置再次出现时, 才被动地重新跟踪到目标。本实例表明, 基于记忆模型的算法可以及时恢复因突然移动而发生的跟踪错误。

视频walking2在第210帧之前被另一人遮挡, 在遮挡人逐渐离开到第215帧, 目标偏离错误地定位到遮挡人。基于记忆模型算法的长时跟踪借助长时记忆模板在第220帧及时纠正了跟踪错误, 并且在遮挡人逐渐离开的过程中多次纠正跟踪误差, 而基本算法则在余下帧中一直延续了跟踪错误。本实例再次表明, 基于记忆模型的算法可以矫正对因为遮挡引起的跟踪错误。

视频girl中目标在第432帧开始被另一人脸遮挡, 到第438帧几乎完全被遮挡。基于记忆模型算法的长时跟踪借助长时记忆模板到第438帧仍然保持正确的定位, 而基本算法则由于使用的是插值更新的方法, 模板逐渐被遮挡人脸取代, 因而到第438帧完全漂移到遮挡人脸上。本实例表明, 基于记忆模型的算法对因为遮挡引起的跟踪错误能够及时矫正。

以上实验结果表明, 基于记忆模型的核化目标跟踪算法可以矫正各种原因(包括姿态变化和光照变化引起的目标外观变化、目标快速移动及遮挡等)引起的跟踪错误。

本文基于记忆模型的核化相关滤波目标跟踪算法, 建立了模板和滤波器的记忆机制。将记忆分为短时记忆和长时记忆库, 模板和滤波器的更新即是记忆的建立、回想、决策、反馈和遗忘。将目标跟踪过程分为短时跟踪和长时跟踪:短时跟踪参照短时记忆, 采用插值模板更新方式, 以保证模板和滤波器的弹性; 长时跟踪参照长时记忆库, 长时记忆库保存了目标稳定的模板和滤波器信息, 用于保证模板和滤波器的稳定性。长时跟踪的设置保证了在各种原因导致的跟踪错误发生时, 能够及时纠错。实验结果表明, 对于遮挡及其他外观变化引起的跟踪错误, 基于记忆模型的模板更新策略有矫正作用, 能够从跟踪失败中恢复。