|
|
|
发布时间: 2022-08-25 |
智能电网技术 |
|
|
|
收稿日期: 2021-12-05
基金项目: 国家自然科学基金(51607110)
中图法分类号: TM724
文献标识码: A
文章编号: 2096-8299(2022)04-0315-07
|
摘要
中继线圈能有效增大磁耦合谐振式无线电能传输(MRC-WPT)系统的传输距离, 但由于其自身的功率损耗, 导致系统总损耗增加, 传输功率下降。提出了一种有源中继结构, 通过向中继线圈赋能, 扩大了发射线圈的能量辐射范围, 在显著增大系统传输距离的同时增大了系统的传输功率, 保证了输出功率恒定。与多发射线圈系统相比, 有源中继系统不需要考虑发射线圈之间的交叉耦合影响, 分析及设计更加方便; 与传统无源中继系统相比, 有源中继系统的最大传输功率高于对应的无源中继系统; 与对应的无中继系统相比, 在增加传输距离的同时, 有源中继系统的最大传输功率能保持与无中继系统相同。仿真结果与理论分析结果一致。
关键词
磁耦合谐振式无线电能传输; 有源中继线圈; 最优位置; 传输功率
Abstract
The transmission distance of magnetic resonant coupling wireless power transfer (MRC-WPT) system can be significantly increased by placing intermediate coils between transmitter and receiver.While the loss of repeaters adds up the loss of the system, causing the decline of system transmission power.An efficient WPT system with active repeaters (ARs) is proposed.The power transmission distance and transmission power are improved and the output power is guaranteed to be constant by empowering the repeater.Compared with the multi-transmitting coil system, the active relay system does not need to consider the influence of cross-coupling between the transmitting coils, and the analysis and design are more convenient.Moreover, AR-based system can attain higher transmission power than the PR-based system.And compared with the non-repeater system, while increasing the transmission distance, AR-based system can attain the same maximum transmission power.Simulation results confirm the conclusions.
Key words
magnetic resonant coupling wireless power transfer; active repeater; optimal location; transmission power
近年来, 磁耦合谐振式无线电能传输(Magnetic Resonant Coupling Wireless Power Transfer, MRC-WPT)技术由于其广泛的适用性成为电力科学的研究热点[1]。无线电能传输系统最关键的性能参数包括传输距离、传输功率、传输效率以及抗偏移能力。为了优化这些性能参数, 研究者们提出了很多优化方法, 如优化线圈结构[2-6], 优化谐振补偿结构及参数[7-9]等。其中, 传输距离增大导致的系统效率下降是制约无线电能传输发展和应用的技术瓶颈。在传输距离发生变化时, 系统的传输功率和效率等性能参数均会发生变化。
为了解决以上问题, 研究者们进行了大量研究。文献[10]通过控制发射线圈和接收线圈的负载作用及改变电源的驱动频率来调节传输距离, 然而其主要是提升了系统在近距离发生频率分裂时的性能, 并没有扩展传输距离。文献[11]采用超导体减小了线圈损耗, 同时增大了传输距离, 但超导材料成本过高。
目前, 为增大传输距离广泛采用的方法是在发射线圈与接收线圈之间加装中继线圈[12-20]。中继线圈是由发射线圈接收能量并将其传递给接收线圈, 在远距离传输时能极大提升系统效率。同时, 实际应用中由于受设备尺寸的限制, 接收线圈通常设计得比发射线圈小, 构成了非对称结构, 故影响了系统的传输功率和效率。
高压输电线路在线监测设备主要使用电池和新能源供电, 但电池的频繁更换和新能源供电的不稳定性制约了智能化设备的发展。文献[20]提出了使用带中继线圈的电磁谐振式无线电能传输技术来进行跨越绝缘距离的无线供电技术, 中继线圈显著增大了传输距离, 但感应式取能装置难以满足某些在线监测设备的供电需求, 并且中继线圈的损耗会进一步增加系统的损耗。
采用多个取能装置为监测设备供电可以满足供电需求。取能装置主要有以下两种结构: 一是2个取能装置连接1个发射线圈, 但发射线圈中电流较大, 线圈的磁场可能对监测设备的工作产生影响; 二是2个取能装置分别连接2个线圈, 类似于多发射线圈的无线电能传输系统, 但多个发射线圈之间的交叉耦合会改变发射线圈的谐振频率。因此, 需要相应改变整个系统的谐振频率及电源的驱动频率, 从而实现传输效率与输出功率的最大化[21-22]。由于线圈沿输电线路分布, 内侧的线圈可以视为带有电源的中继线圈, 即有源中继线圈。这种结构将电源分散布置于发射线圈和各个中继线圈中, 具有多发射线圈系统可靠性高的特点, 同时位于首末2个线圈之间的线圈起到中继作用, 增大了系统的传输功率。在多发射线圈系统中, 各个发射线圈的电源需要严格整定来维持传输功率的稳定[23], 而有源中继系统的电源只需保持其频率与系统工作频率相同, 且中继线圈结构可显著提高系统设计的灵活性[24]。
针对远距离磁谐振式无线电能传输, 本文提出了一种新型的有源中继谐振式无线电能传输系统(以下简称“有源中继系统”)。在传输距离增大的同时, 保证了系统的传输功率。另外, 分布式电源结构提升了系统的可靠性, 使系统运行更加灵活, 不会由于发射线圈故障而停止工作, 适用于对可靠性要求较高的工况。选取3种不同尺寸的接收线圈分别对有源中继系统、对应的无源中继系统及无中继系统进行对比实验, 验证了理论分析的正确性。
1 有源中继系统概述
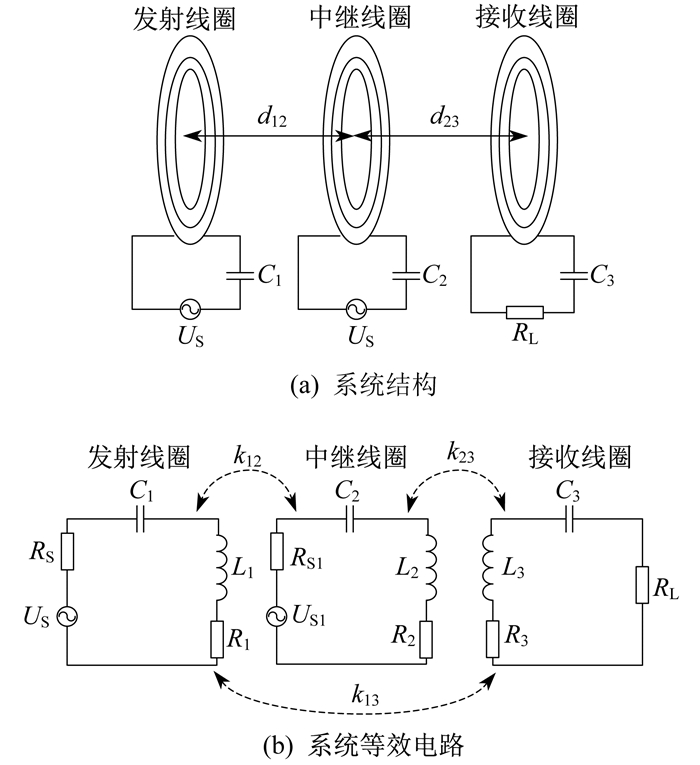
有源中继系统由发射线圈、有源中继线圈和接收线圈组成。以含单个有源中继线圈的三线圈系统为例, 对有源中继系统进行建模及分析。图 1为有源中继系统模型及等效电路图。
图 1(a)中含有3个谐振回路, 即发射线圈(线圈1)回路、中继线圈(线圈2)回路和接收线圈(线圈3)回路, 分别用下标1, 2, 3区分各个线圈的参数。各谐振回路均采用串联补偿。线圈的中心在一条直线上, 线圈之间的距离分别为d12和d23。图 1(b)中, 发射线圈连接交流电源US, 电源内阻为RS, 线圈之间的耦合系数分别为k12, k23, k13。有源中继线圈与发射线圈类似, 连接交流电源US1, 电源内阻为RS1, 接收线圈与负载RL连接。Li和Ri表示各个线圈i(i=1, 2, 3)的自感和等效串联电阻(Equivalent Series Resistance, ESR), Ci表示线圈i串联的补偿电容, 其ESR相对较小, 可以忽略。
各个线圈工作于相同的谐振角频率, 即
| $ \omega_0=\frac{1}{\sqrt{L_1 C_1}}=\frac{1}{\sqrt{L_2 C_2}}=\frac{1}{\sqrt{L_3 C_3}} $ | (1) |
对图 1(b)中的等效电路使用回路电流法, 可列出系统的回路电流方程为
| $ \left\{\begin{array}{l} Z_1 I_1+\mathrm{j} \omega M_{12} I_2+\mathrm{j} \omega M_{13} I_3=U_{\mathrm{S}} \\ \mathrm{j} \omega M_{12} I_1+Z_2 I_2+\mathrm{j} \omega M_{23} I_3=U_{\mathrm{S} 1} \\ \mathrm{j} \omega M_{13} I_1+\mathrm{j} \omega M_{23} I_2+Z_3 I_3=0 \end{array}\right. $ | (2) |
其中,
| $ \left\{\begin{array}{l} Z_1=R_{\mathrm{S}}+\mathrm{j} \omega \ L_1+\frac{1}{\mathrm{j} \omega \ C_1}+R_1 \\ Z_2=R_{\mathrm{S} 1}+\mathrm{j} \omega \ L_2+\frac{1}{\mathrm{j} \omega \ C_2}+R_2 \\ Z_3=R_{\mathrm{L}}+\mathrm{j} \omega \ L_3+\frac{1}{\mathrm{j} \omega \ C_3}+R_3 \end{array}\right. $ | (3) |
式中: Ii——有源中继系统各回路的电流;
j——复数虚部符号;
ω——系统工作的角频率;
M12, M13, M23——两个线圈之间的互感。
两个线圈之间的互感与耦合系数的关系为
| $ M_{i k}=k_{i k} \sqrt{L_i L_k}, \quad i, k=1, 2, 3 $ | (4) |
为简化分析, 令发射线圈与接收线圈之间的耦合系数为零, 即k13=0;同时, 发射线圈和中继线圈的电源相同, 即US=US1, RS=RS1, 则可以根据式(2) 求出各回路电流为
| $\left\{\begin{array}{l} I_1=\frac{U_{\mathrm{S}}\left(Z_2 Z_3+\omega^2 M_{23}^2-\mathrm{j} \omega M_{12} Z_3\right)}{Z_1 Z_2 Z_3+\omega^2 M_{12}^2 Z_3+\omega^2 M_{23}^2 Z_1} \\ I_2=\frac{U_{\mathrm{S}}\left(Z_1 Z_3-\mathrm{j} \omega M_{12} Z_3\right)}{Z_1 Z_2 Z_3+\omega^2 M_{12}^2 Z_3+\omega^2 M_{23}^2 Z_1} \\ I_3=\frac{-\omega M_{23} U_{\mathrm{S}}\left(\omega M_{12}+\mathrm{j} Z_1\right)}{Z_1 Z_2 Z_3+\omega^2 M_{12}^2 Z_3+\omega^2 M_{23}^2 Z_1} \end{array}\right. $ | (5) |
2 有源及无源中继系统传输功率分析
2.1 有源中继系统传输功率分析
当系统工作于谐振频率, 即ω=ω0时, 有
| $ \mathrm{j} \omega_0 L_i+\frac{1}{\mathrm{j} \omega_0 C_i}=0, \quad i=1, 2, 3 $ | (6) |
各个线圈的品质因数Qi及类品质因数Qi*(不考虑线圈的等效串联电阻)分别为
| $ \left\{\begin{array}{l} Q_1=\frac{\omega_0 L_1}{R_{\mathrm{S}}+R_1} \\ Q_2=\frac{\omega_0 L_2}{R_{\mathrm{S}}+R_2} \\ Q_3=\frac{\omega_0 L_3}{R_{\mathrm{L}}+R_3} \end{array}\right. $ | (7) |
| $\left\{\begin{array}{l} Q_1^*=\frac{\omega_0 L_1}{R_1} \\ Q_2^*=\frac{\omega_0 L_2}{R_2} \\ Q_3^*=\frac{\omega_0 L_3}{R_{\mathrm{L}}} \end{array}\right. $ | (8) |
传输到接收回路的功率为
| $ \begin{aligned} &P_{\mathrm{out}}=I_3^2 R_{\mathrm{L}}= \\ &\frac{U_{\mathrm{S}}^2\left(k_{12}^2 k_{23}^2 \frac{Q_1 Q_2^2 Q_3^2}{Q_3^*}+k_{23}^2 \frac{Q_2 Q_3^2}{Q_3^*}\right)}{\left(R_{\mathrm{S}}+R_1\right)\left(1+k_{12}^2 Q_1 Q_2+k_{23}^2 Q_2 Q_3\right)^2} \end{aligned} $ | (9) |
2.2 无源中继系统传输功率分析
对系统参数与上述有源中继系统相同的无源中继系统进行分析。系统的回路电流方程为
| $\left\{\begin{array}{l} Z_1 I_1{ }^{\prime}+\mathrm{j} \omega M_{12} I_2{ }^{\prime}+\mathrm{j} \omega M_{13} I_3{ }^{\prime}=U_{\mathrm{s}} \\ \mathrm{j} \omega M_{12} I_1{ }^{\prime}+Z_2^{\prime} I_2{ }^{\prime}+\mathrm{j} \omega M_{23} I_3{ }^{\prime}=0 \\ \mathrm{j} \omega M_{13} I_1{ }^{\prime}+\mathrm{j} \omega M_{23} I_2{ }^{\prime}+Z_3 I_3{ }^{\prime}=0 \end{array}\right. $ | (10) |
式中: I′i——无源中继系统各回路的电流;
| $ Z_2^{\prime}=\mathrm{j} \omega L_2+\left(1 / \mathrm{j} \omega C_2\right)+R_2 。$ |
同样地, 忽略发射线圈与接收线圈之间的交叉耦合, 则各回路电流为
| $ \left\{\begin{array}{l} I_1{ }^{\prime}=\frac{U_{\mathrm{S}}\left(Z_2{ }^{\prime} Z_3+\omega^2 M_{23}^2\right)}{Z_1 Z_2{ }^{\prime} Z_3+\omega^2 M_{12}^2 Z_3+\omega^2 M_{23}^2 Z_1} \\ I_{2}^{\prime}=\frac{-U_{\mathrm{S}} \mathrm{j} \omega M_{12} Z_3}{Z_1 Z_2{ }^{\prime} Z_3+\omega^2 M_{12}^2 Z_3+\omega^2 M_{23}^2 Z_1} \\ I_3{ }^{\prime}=\frac{-U_{\mathrm{S}} \omega^2 M_{23} M_{12}}{Z_1 Z_2{ }^{\prime} Z_3+\omega^2 M_{12}^2 Z_3+\omega^2 M_{23}^2 Z_1} \end{array}\right. $ | (11) |
所有线圈的品质因数和类品质因数与有源中继系统相同。传输到接收回路的功率为
| $ \begin{array}{l} P_{{\rm{out }}}^\prime = I_3^{\prime 2}{R_{\rm{L}}} = \\ \frac{{U_{\rm{S}}^2\left( {k_{12}^2k_{23}^2\frac{{{Q_1}Q_2^{*2}Q_3^2}}{{Q_3^*}}} \right)}}{{\overline {\left( {{R_{\rm{S}}} + {R_1}} \right){{\left( {1 + k_{12}^2{Q_1}Q_2^* + k_{23}^2Q_2^*{Q_3}} \right)}^2}} }} \end{array} $ | (12) |
2.3 两种中继系统传输功率对比
为便于分析及实验验证, 假设发射线圈与有源中继线圈之间距离固定, 通过求解得到使系统传输功率最大的耦合系数k23, 由此确定接收线圈的最佳位置, 同时得到系统对应的最大传输功率。
2.3.1 有源中继系统
磁耦合谐振式无线电能传输系统存在频率分裂现象, 因此在临界耦合时系统的传输功率最大。通过调整接收线圈的位置, 可以使系统达到临界耦合状态。
由式(8)可得:
| $ \begin{aligned} \frac{\mathrm{d} P_{\text {out }}}{\mathrm{d} k_{23}}=& \frac{U_{\mathrm{S}}^2\left(k_{12}^2 2 k_{23} \frac{Q_1 Q_2^2 Q_3^2}{Q_3^*}+2 k_{23} \frac{Q_2 Q_3^2}{Q_3^*}\right)\left(R_{\mathrm{S}}+R_1\right)\left(1+k_{12}^2 Q_1 Q_2+k_{23}^2 Q_2 Q_3\right)^2}{\left(R_{\mathrm{S}}+R_1\right)^2\left(1+k_{12}^2 Q_1 Q_2+k_{23}^2 Q_2 Q_3\right)^4}-\\ & \frac{U_{\mathrm{S}}^2\left(k_{12}^2 k_{23}^2 \frac{Q_1 Q_2^2 Q_3^2}{Q_3^*}\right)\left(R_{\mathrm{S}}+R_1\right) 2\left(1+k_{12}^2 Q_1 Q_2+k_{23}^2 Q_2 Q_3\right) 2 k_{23} Q_2 Q_3}{\left(R_{\mathrm{S}}+R_1\right)^2\left(1+k_{12}^2 Q_1 Q_2+k_{23}^2 Q_2 Q_3\right)^4} \end{aligned} $ | (13) |
令dPout/dk23=0, 得到使系统传输功率最大的接收线圈位置(最优位置)对应的临界耦合系数为
| $ k_{23\text{opt }}=\frac{k_{12}^2 Q_1 Q_2+1}{\sqrt{k_{12}^2 Q_1 Q_2^2 Q_3+Q_2 Q_3}} $ | (14) |
可以看出, k23opt是由各线圈的品质因数决定的。在发射线圈和中继线圈的结构确定(即Q1和Q2确定)时, 接收线圈的品质因数Q3将决定接收线圈的最佳位置。
将式(14)代入式(8), 可得到接收线圈处于最优位置时对应的系统传输功率为
| $ P_{\text {outopt }}=\frac{U_{\mathrm{S}}^2\left(k_{12}^2 Q_1 Q_2 Q_3+Q_3\right)}{4 Q_3^*\left(R_{\mathrm{S}}+R_1\right)\left(1+k_{12}^2 Q_1 Q_2\right)} $ | (15) |
若发射线圈与中继线圈相同, 令Q=Q1=Q2, Q*=Q1*=Q2*, 则式(15)变为
| $P_{\text {outopt }}=\frac{U_{\mathrm{S}}^2 Q_3}{4 Q_3^*\left(R_{\mathrm{S}}+R_1\right)} $ | (16) |
由文献[11]可得传统两线圈系统的最大传输功率为
| $ P_{\text {outopt0 }}=\frac{U_{\mathrm{S}}^2 Q_3}{4 Q_3^*\left(R_{\mathrm{S}}+R_1\right)}=P_{\text {outopt }} $ | (17) |
由式(17)可知, 若有源中继系统的发射线圈与无中继系统相同, 则有源中继系统的最大传输功率与无中继系统也相同。
2.3.2 无源中继系统
对于无源中继系统, 同样地, 由式(12), 令dP′out/dk23=0, 得到临界耦合系数为
| $k_{23 \mathrm{opt}}^{\prime}=\sqrt{\frac{k_{12}^2 Q_1 Q_2^*+1}{Q_2^* Q_3}} $ | (18) |
将式(18)代入式(12), 得到无源中继系统的最大传输功率为
| $ P_{\text {outopt }}^{\prime}=\frac{U_{\mathrm{S}}^2 k_{12}^2 Q_1 Q_2^* Q_3}{4 Q_3^*\left(R_{\mathrm{S}}+R_1\right)\left(1+k_{12}^2 Q_1 Q_2^*\right)} $ | (19) |
若发射线圈与中继线圈相同, 此时令Q=Q1=Q2, Q*=Q1*=Q2*, 则式(19)变为
| $ P_{\text {outopt }}^{\prime}=\frac{U_{\mathrm{S}}^2 k_{12}^2 Q Q^* Q_3}{4 Q_3^*\left(R_{\mathrm{S}}+R_1\right)\left(1+k_{12}^2 Q Q^*\right)} $ | (20) |
2.3.3 对比分析
根据上述分析可以对两种系统的性能进行比较。
| $ \begin{gathered} P_{\text {outopt }}-P_{\text {outopt }}^{\prime}=\frac{U_{\mathrm{S}}^2 Q_3}{4 Q_3^*\left(R_{\mathrm{S}}+R_1\right)}- \\ \frac{U_{\mathrm{S}}^2 k_{12}^2 Q Q^* Q_3}{4 Q_3^*\left(R_{\mathrm{S}}+R_1\right)\left(1+k_{12}^2 Q Q^*\right)}= \\ \frac{U_{\mathrm{S}}^2 Q_3}{4 Q_3^*\left(R_{\mathrm{S}}+R_1\right)\left(1+k_{12}^2 Q Q^*\right)}= \\ \frac{U_{\mathrm{S}}^2 R_{\mathrm{L}}}{4\left(R_{\mathrm{L}}+R_3\right)\left(R_{\mathrm{S}}+R_1\right)\left(1+k_{12}^2 Q Q^*\right)}>0 \end{gathered} $ | (21) |
式(21)说明了对于参数相同的两种系统, 有源中继系统的最大传输功率始终高于无源中断系统, 而且接收线圈的电阻R3越小, 两者的差越大。
3 实验验证
图 2为实验系统的实物照片及实验所采用的线圈。
线圈均由400股AWG-38利兹线绕制以减小集肤效应和邻近效应。发射线圈与中继线圈完全相同。接收线圈采用3种不同的尺寸和匝数, 按其相对于发射线圈的尺寸划分为3种情况: 比发射线圈小为Small RX; 与发射线圈相同为Medium RX; 比发射线圈大为Large RX。电源内阻及负载电阻均为50 Ω。系统谐振频率设置为6.78 MHz。系统参数如表 1所示。根据表 1和式(14), 计算得到3种情况下有源中继系统的临界耦合系数理论计算值分别为0.169, 0.138, 0.113。
表 1
实验系统参数
| 参数 | 发射线圈 | 中继线圈 | Small RX | Medium RX | Large RX |
| US/V | 200.00 | 200.00 | |||
| f/MHz | 6.78 | 6.78 | 6.78 | 6.78 | 6.78 |
| R/cm | 10 | 10 | 10 | 10 | 10 |
| 匝数/匝 | 7 | 7 | 5 | 7 | 10 |
| Li/μH | 14.11 | 14.07 | 9.20 | 14.07 | 21.78 |
| Ri/Ω | 5.27 | 5.15 | 4.02 | 5.16 | 7.39 |
| Qi | 10.87 | 10.87 | 7.26 | 10.87 | 16.16 |
| Qi* | 12.02 | 12.02 | 7.84 | 12.02 | 18.55 |
| Ci/pF | 39.20 | 39.20 | 59.90 | 39.20 | 25.30 |
实验采用矢量网络分析仪(Vector Network Analyzer, VNA)Keysight E5061B, 利用其自带的选件006(无线功率传输分析选件)可对系统的输入输出电压或电流、输出功率、系统效率等参数进行精确测量。实验中保持发射线圈与中继线圈的距离d12=10 cm, 使接收线圈与中继线圈之间的距离由5 cm增加到35 cm, 则d13∈[15 cm, 45 cm]。对于无中继系统, 由于没有中继线圈, 故d13∈[5 cm, 35 cm]。
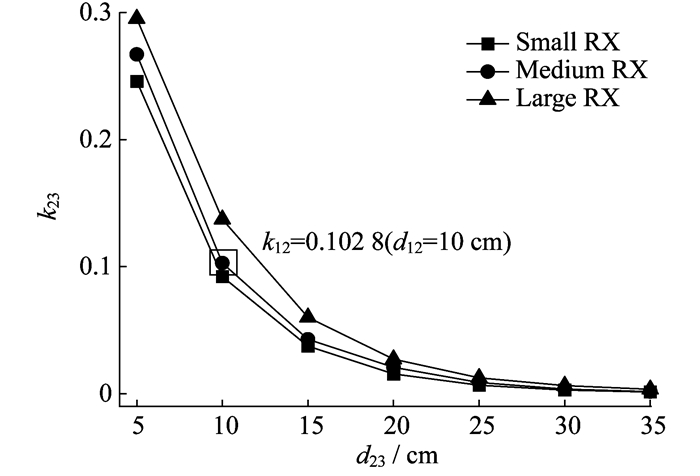
对于3种不同的接收线圈, k23与d23之间的关系如图 3所示。由图 3可以看出, 耦合系数均随着线圈之间距离的增大而减小, 并且k23随着接收线圈匝数的增多而变大。
由于中继线圈与接收线圈之间的距离d12=10 cm, 因此耦合系数k12=0.102 8。
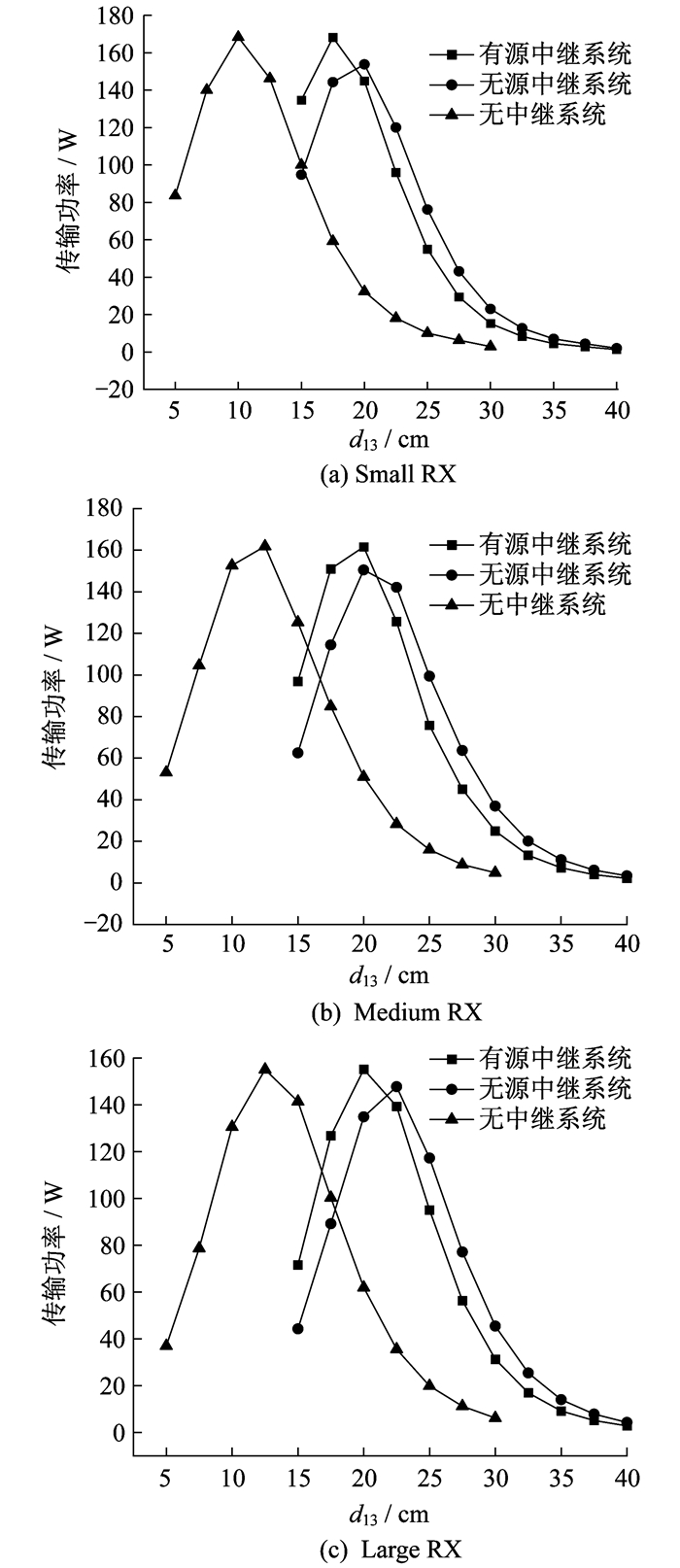
图 4为传输距离d23与系统传输功率的关系, 当d23较小时, 有源中继系统的传输功率高于无源中继系统。而当d23较大时, 情况相反。将式(9)与式(12)作差可得
| $ \begin{aligned} \Delta P_{\mathrm{out}}=& \frac{U_{\mathrm{S}}^2\left(k_{12}^2 k_{23}^2 \frac{Q_1 Q_2^2 Q_3^2}{Q_3^*}+k_{23}^2 \frac{Q_2 Q_3^2}{Q_3^*}\right)}{\left(R_{\mathrm{S}}+R_1\right)\left(1+k_{12}^2 Q_1 Q_2+k_{23}^2 Q_2 Q_3\right)^2}-\\ & \frac{U_{\mathrm{S}}^2\left(k_{12}^2 k_{23}^2 \frac{Q_1 Q_2^{* 2} Q_3^2}{Q_3^*}\right)}{\left(R_{\mathrm{S}}+R_1\right)\left(1+k_{12}^2 Q_1 Q_2^*+k_{23}^2 Q_2^* Q_3\right)^2}=\\ & \frac{U_{\mathrm{S}}^2}{A_1} \cdot \frac{1}{A_2} \cdot A_3 \end{aligned} $ | (22) |
其中,
| $ A_1=\left(R_{\mathrm{S}}+R_1\right)\left(1+k_{12}^2 Q_1 Q_2+k_{23}^2 Q_2 Q_3\right)^2 $ | (23) |
| $ A_2=\left(R_{\mathrm{S}}+R_1\right)\left(1+k_{12}^2 Q_1 Q_2^*+k_{23}^2 Q_2^* Q_3\right)^2 $ | (24) |
| $ A_3=\left[k_{12}^2 k_{23}^2 \frac{Q_1 Q_3^2\left(Q_2^2-Q_2^{* 2}+2 Q_2 Q_2^*\right)}{Q_3^*}+\right.\\ k_{23}^2 \frac{Q_2 Q_3^2}{Q_3^*}+k_{23}^4 \frac{Q_2 Q_2^* Q_3^2}{Q_3^*}+ \\ k_{12}^4 k_{23}^2 \frac{Q_1^2 Q_3^2 Q_2 Q_2^*\left(2 Q_2-Q_2^*\right)}{Q_3^*}+ \\ \left.k_{12}^2 k_{23}^4 \frac{Q_1 Q_3^3 Q_2 Q_2^*\left(2 Q_2-Q_2^*\right)}{Q_3^*}\right] $ | (25) |
| $ 2 Q_2-Q_2^*=\frac{\omega_0 L_2\left(R_2-R_{\mathrm{S}}\right)}{\left(R_{\mathrm{S}}+R_2\right) R_2} $ | (26) |
| $ Q_2^2-Q_2^{* 2}+2 Q_2 Q_2^*=\frac{\omega_0^2 L_2^2\left(2 R_2^2-R_{\mathrm{S}}^2\right)}{\left(R_{\mathrm{S}}+R_2\right)^2 R_2^2} $ | (27) |
由式(26)和式(27)看出, 当R2>RS时, 就可以满足有源中继系统的输出功率一直高于无源中继系统。
由图 4可以看出, 3种不同尺寸发射线圈对应的有源中继系统的最大传输功率均与相应的无中继系统相同, 且高于对应的无源中继系统。这与式(17)和式(21)的分析结果一致。同时, 接收线圈Small RX的电阻R3最小, 对应的有源中继系统比无源中继系统的最大传输功率提高了8.3%;接收线圈Medium RX的R3居中, 最大传输功率提高了7.4%;接收线圈Large RX的R3最大, 最大传输功率提高了5.8%。因此, R3越小, 最大传输功率提高的幅度就越大, 这与式(21)的分析结果一致。
4 结语
本文研究了有源中继谐振式无线电能传输系统的传输特性。根据等效电路模型, 在固定发射线圈及中继线圈的相对位置时, 得出了使有源中继系统取得最大传输功率的接收线圈位置。理论分析表明, 有源中继系统的最大传输功率高于对应的无源中继系统, 且接收线圈的电阻越小, 两者的差值越大。与对应无中继系统相比, 在增加传输距离的同时, 有源中继系统的最大传输功率能保持与无中继系统相同。选取3种不同尺寸的接收线圈, 分别对有源中继系统及其对应的无源中继系统、无中继系统进行对比实验, 实验结果验证了理论分析的正确性。
参考文献
-
[1]黄学良, 王维, 谭林林. 磁耦合谐振式无线电能传输技术研究动态与应用展望[J]. 电力系统自动化, 2017, 41(2): 2-14.
-
[2]ZHANG X X, LUO B, HU Y, et al. A novel dumbbell-shaped coil featured with cross coupling suppression for long distance relay wireless power transfer applications[J]. IEICE Electronics Express, 2017, 14(19): 1-11.
-
[3]李阳, 马靖男, 李明, 等. 无线电能传输磁耦合线圈的设计与优化[J]. 电器与能效管理技术, 2019(17): 56-62.
-
[4]戴欣, 李璐, 余细雨, 等. 基于正四面体的无线电能传输系统多自由度电能拾取机构[J]. 中国电机工程学报, 2016, 36(23): 6460-6467.
-
[5]ZAHEER A, HAO H, COVIC G A, et al. Investigation of multiple decoupled coil primary pad topologies in lumped IPT systems for interoperable electric vehicle charging[J]. IEEE Transactions on Power Electronics, 2015, 30(4): 1937-1955. DOI:10.1109/TPEL.2014.2329693
-
[6]张肖雄. 基于新型哑铃型线圈的无线电能传输网络研究[D]. 南昌: 南昌大学, 2018.
-
[7]ZHANG W, MI C C. Compensation topologies of high-power wireless power transfer systems[J]. IEEE Transactions on Vehicular Technology, 2016, 65(6): 4768-4778. DOI:10.1109/TVT.2015.2454292
-
[8]麦瑞坤, 陈阳, 刘野然. 基于变补偿参数的IPT恒流恒压电池充电研究[J]. 中国电机工程学报, 2016, 36(21): 5816-5821.
-
[9]陈庆彬, 张伟豪, 叶逢春, 等. 结合变压器T网络模型的具有可变恒压增益特性的补偿网络参数确定新方法[J]. 中国电机工程学报, 2017, 37(15): 4483-4494.
-
[10]管乐诗, 肖扬雲, 王懿杰, 等. 一种基于PCB平面螺旋线圈的自补偿多中继无线电能传输系统设计[J/OL]. 中国电机工程学报: 1-10[2021-12-29]. http://hp.kns.cnki.net.shiep.vpn358.com/kcms/detail/11.2107.tm.2021029.1644.007.html.
-
[11]陈庆彬, 杨丰钢, 陈为. 具有可变增益恒压特性的三线圈WPT系统补偿网络结构及参数确定新方法[J]. 中国电机工程学报, 2021, 41(6): 2277-2289.
-
[12]SAMPATH J P K, ALPHONES A, VILATHGAMUWA D M. Optimization of wireless power transfer system with a repeater against load variations[J]. IEEE Transactions on Industrial Electronics, 2017, 64(10): 7800-7809. DOI:10.1109/TIE.2017.2696499
-
[13]宋凯, 朱春波, 李阳, 等. 基于磁耦合谐振的自主无线充电机器人系统设计[J]. 电工技术学报, 2014, 29(9): 38-43.
-
[14]张淑美, 李媛, 程泽. 三线圈无线电能传输系统传输特性的研究[J]. 湖南大学学报(自然科学版), 2021, 48(8): 68-77.
-
[15]SAMPATH J P K, ALPHONES A, VILATHGAMUWA D M. Repeater tuning against load variation for wireless power transfer[C]//The 2016 8th International Power Electronics and Motion Control Conference. Hefei: IEEE, 2016: 3173-3177.
-
[16]王宇, 龚国庆. 磁耦合谐振式无线电能传输系统三线圈结构研究[J]. 北京信息科技大学学报(自然科学版), 2021, 36(3): 92-96.
-
[17]ZHANG J, YUAN X, WANG C, et al. Comparative analysis of two-coil and three-coil structures for wireless power transfer[J]. IEEE Transactions on Power Electronics, 2016, 32(1): 341-352.
-
[18]YE Z H, SUN Y, DAI X, et al. Energy efficiency analysis of u-coil wireless power transfer system[J]. IEEE Transactions on Power Electronics, 2016, 31(7): 4809-4817.
-
[19]LEE K, CHAE S H. Effect of quality factor on determining the optimal position of a transmitter in wireless power transfer using a relay[J]. IEEE Microwave & Wireless Components Letters, 2017, 27(5): 521-523.
-
[20]黄智慧, 邹积岩, 王永兴, 等. 基于中继线圈的WPT技术及其在高压设备中的应用研究[J]. 电工技术学报, 2015, 30(11): 45-52.
-
[21]吴晓春, 田孟林, 连海生, 等. 双发射结构磁谐振式无线电能传输系统传输特性研究[J]. 上海电力学院学报, 2019, 35(4): 321-326.
-
[22]DUONG Q T, OKADA M. Maximum efficiency formulation for multiple-input multiple-output inductive power transfer systems[J]. IEEE Transactions on Microwave Theory & Techniques, 2018, 66(7): 3463-3477.
-
[23]GUO J, TAN L, LIU H, et al. Stabilization control of output power in double-source wireless power transfer systems without direct output feedback[J]. IEEE Microwave & Wireless Components Letters, 2016, 26(11): 960-962.
-
[24]罗斌, 刘婉, 钟晨明, 等. 磁耦合谐振三线圈无线电能传输的交叉耦合效应及电抗补偿[J]. 电力系统自动化, 2015, 39(8): 105-112.