二阶RLC串联电路的暂态过程, 在电力生产实际中比较常见。高压直流输电换流器在电流不连续工况下的阀触发导通为工频激励下二阶电路过程。在控制工程中, 二阶系统有很重要的地位, 这不仅是因为二阶系统在数学上容易分析, 更是因为可以将高阶系统降为二阶系统进行处理, 仍不失其运动过程的基本性质^[1]。

二阶RLC电路暂态过程的响应由一个二阶线性常系数微分方程求解, 电路理论及高等数学有成熟的解法^[2-3]。自动控制原理在上述基础上引入一个阻尼系数进行讨论。求解微分方程可以得出特征根, 因电路参数不同其根为3种情况, 对应的响应结果是过阻尼的非振荡型和欠阻尼的振荡型及临界型。文献[4-8]就暂态响应结果和电路参数的关系进行了讨论, 对不同的电路参数给出了仿真结果。本文通过引入一个振荡系数, 简化了二阶电路暂态响应的计算公式, 对非振荡型响应提出了二阶RLC电路的响应近似等同于一阶RC电路的响应条件, 对振荡型响应提出了简明的判断振荡频率周期和衰减趋势方法。同时, 列举一个高压直流输电的二阶电路的暂态过程算例^[9], 并利用MATLAB/Simulink进行仿真^[10], 验证了理论推导的正确性。

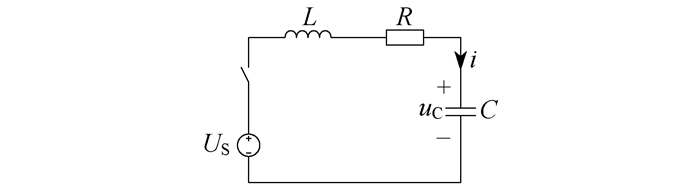
二阶串联RLC电路如图 1所示。

图 1中, L, R, C分别为电感、电阻和电容, U_S为直流激励电压, u_C和i为响应电压和电流, u_C(0)=U_C0为零输入响应的初值。

二阶串联RLC电路的零输入响应的微分方程为

$ L C \frac{\mathrm{d}^2 u_{\mathrm{C}}}{\mathrm{d}^2 t}+R C \frac{\mathrm{d} u_{\mathrm{C}}}{\mathrm{d} t}+u_{\mathrm{C}}=0 $

(1)

求解这种类型的微分方程可以得出特征根, 根据电路参数不同可分为一对不同的负实根、一对相同的负实根或一对共轭复根3种情况。对于第1种情况, 电路的响应为非振荡型, 设δ=R/2L, $ \omega_0=1 / \sqrt{L C} $, ω²=δ²－ω₀², 则特征根－r_{1, 2}=－δ±ω, 非振荡型判别条件是δ>ω₀。

引入一个参数m, 令m=ω₀²/δ²=(4L/R)/RC。非振荡判别条件m < 1, 可得$ \omega=\sqrt{1-m} \times \delta $, 则$ -r_1=-(1-\sqrt{1-m}) \times \delta $, $ -r_2=-(1+\sqrt{1-m}) \times \delta $。另有L/R=mRC/4, δ=R/2L=2/mRC。对于一对共轭复根的情况, 电路的响应为振荡型, 判别条件δ < ω₀或m>1, 设ω²=ω₀²－δ², 可得$ \omega=\sqrt{m-1} \times \delta $, 则特征根为$-r_{1, 2}=-\delta\pm j(\sqrt{m-1}) \delta $。其中, m为振荡系数, δ, ω, ω₀分别为衰减因子、振荡角频率和无阻尼振荡角频率。

对于电路的响应为非振荡型, 其微分方程的通解为

$ u_{\mathrm{C}}=A_1 \mathrm{e}^{-r_1 t}+A_2 \mathrm{e}^{-r_2 t} $

(2)

式中: A₁, A₂——根据初始条件确定的常数。

利用参数m对零输入响应通解的两项系数进行比较。由初始条件$ u_{\mathrm{C}}(0)=U_{\mathrm{C} 0}, \left.\frac{\mathrm{d} u_{\mathrm{C}}}{\mathrm{d} t}\right|_{t=0}=0 $, 可得:

$ A_1+A_2=U_{\mathrm{C} 0} $

(3)

$ -r_1 A_1-r_2 A_2=0 $

(4)

式(3)×r₂+式(4)得

$ A_1=\frac{r_2 U_{\mathrm{C} 0}}{r_2-r_1}=\frac{1+\sqrt{1-m}}{2 \sqrt{1-m}} U_{\mathrm{C} 0} $

(5)

式(3)×r₁+式(4)得

$A_2=\frac{-r_1 U_{\mathrm{C} 0}}{r_2-r_1}=\frac{-(1-\sqrt{1-m})}{2 \sqrt{1-m}} U_{\mathrm{C} 0} $

(6)

由式(4)得

$ -\frac{A_1}{A_2}=\frac{r_2}{r_1}=\frac{1+\sqrt{1-m}}{1-\sqrt{1-m}}=k $

(7)

式中: k——通解两项系数的比值, 仅是m值的函数, 其随m值变化如表 1所示。

表 1中, $ A_1=\frac{k}{k-1} U_{\mathrm{C0}}, A_2=\frac{-1}{k-1} U_{\mathrm{C0}} $。

当t=1/r₂=τ₂时刻, 计算m为0.1, 0.3, 0.5, 0.8时通解第1项和第2项的比值$ -\left(u_{\mathrm{C1}} / u_{\mathrm{C} 2}\right)=-\left(A_1 \mathrm{e}^{-r_1 t} / A_2 \mathrm{e}^{-r_2 t}\right)=k \mathrm{e} \times \mathrm{e}^{-1 / k} $, k值较大时用级数展开$ -\left(u_{\mathrm{C} 1} / u_{\mathrm{C} 2}\right) \approx k \mathrm{e} \times(1-1 / k) $。振荡系数m=0.5时通解第1项和第2项的比值等于13.26, 忽略通解第2项造成的结果误差(小于10%), τ₂时刻后的结果误差更小。

再讨论响应通解第1项的衰减系数－r₁和一阶RC电路的衰减系数-1/RC的关系。m值和电感L成正比, 与电容C成反比, 与电阻R的平方成反比, L减少而C和R不变时导致m值变化。响应通解第1项的衰减系数为

$ \begin{aligned} -r_1=&-(1-\sqrt{1-m}) \times \delta=\\ & \frac{-(1-\sqrt{1-m}) \times 2}{m} \times \frac{1}{R C}=\\ & \frac{-2}{(1+\sqrt{1-m})} \times \frac{1}{R C} \end{aligned} $

(8)

设$ K(m)=\frac{2}{(1+\sqrt{1-m})} $, 则, $-r_1=-K(m) \times \frac{1}{R C} $, K(m)和m值的关系如表 2所示。m=0即为电感L减少到零, 这时二阶RLC电路转变为一阶RC电路。

由表 2可知, m=0.3时, K(0.3)=1.090, 则r₁和一阶RC电路的衰减系数接近, 因为响应通解第二项可以忽略, 所以二阶RLC电路的零输入响应近似等同于一阶RC电路的响应。直流激励下的全响应性质相同, 因此可以得出类似结论。

响应电流讨论如下: $ i=C \frac{\mathrm{d} u_{\mathrm{C}}}{\mathrm{d} t}=C\left(-A_1 r_1 \mathrm{e}^{-r_1 t}-\right.\left.A_2 r_2 \mathrm{e}^{-r_2 t}\right) $, 由－r₁A₁=r₂A₂得i=－A₁r₁C×(e^－r₁t－e^－r₂t), 化为$ i=-\frac{1}{\sqrt{1-m}} \times \frac{U_{\mathrm{C} 0}}{R} \times\left(\mathrm{e}^{-r_1 t}-\mathrm{e}^{-r_2 t}\right) $。若m=0.1则$ i=-1.054 \frac{U_{\mathrm{C} 0}}{R} \times\left(\mathrm{e}^{-r_1 t}-\mathrm{e}^{-r_2 t}\right) $, 又因r₂t/r₁t=k=39.9, 所以通解第2项快速衰减, 响应接近一阶RC电路。

对于振荡欠阻尼型, 其微分方程通解为

$u_{\mathrm{C}}=\mathrm{e}^{-\delta t}\left[A_1 \cos (\omega t)+A_2 \sin (\omega t)\right] $

(9)

由零输入响应的初始条件, 可得A₁=U_C0, A₂ω－δA₁=0, 所以,

$u_{\mathrm{C}}=\mathrm{e}^{-\delta t}\left[U_{\mathrm{C} 0} \cos (\omega t)+U_{\mathrm{C} 0} \frac{\delta}{\omega} \sin (\omega t)\right] $

(10)

化为

$ u_{\mathrm{C}}=\frac{U_{\mathrm{C} 0} \omega_0}{\omega} \mathrm{e}^{-\delta t} \sin (\omega t+\beta) $

(11)

而β=arctan ω/δ, 回路电流为

$i=-C \frac{\mathrm{d} u_{\mathrm{C}}}{\mathrm{d} t}=\frac{U_{\mathrm{C} 0}}{\omega L} \mathrm{e}^{-\delta t} \sin (\omega t) $

(12)

引入振荡系数m, 则$ \omega_0=\sqrt{m} \times \delta, \omega=\sqrt{m-1} \times \delta $, 可得以下简明关系: $\beta=\arctan \sqrt{m-1}, \sin \beta=\frac{\omega}{\omega_0}=\frac{\sqrt{m-1}}{\sqrt{m}} $。振荡周期为$ T_\omega=\frac{2 {\rm{ \mathsf{ π} }}}{\omega} $, 设无阻尼时振荡周期为$ T_0=2 {\rm{ \mathsf{ π} }} \sqrt{L C} $, 则$ \frac{T_\omega}{T_0}=\frac{\sqrt{m}}{\sqrt{m-1}}$。电路暂态阻抗$ \omega L=\frac{\sqrt{m-1}}{\sqrt{m}} \omega_0 L $或$ \omega L=\sqrt{m-1} \delta L=\frac{\sqrt{m-1}}{2} R $; 无阻尼时电路暂态阻抗$\omega_0 L=Z_0=\sqrt{\frac{L}{C}} $。

在上述结果的基础上, 利用振荡系数m对响应与元件参数关系进行分析, 发现振荡频率和周期、响应的电压幅值的衰减系数e^－δt随系数m的变化规律。假定L, C值不变, R值减少使m值从1.1增大到1 000对电路响应特性的影响如表 3所示。

振荡经过整数倍的半周期时刻的响应值可表示为简明的式子。设ωt=kπ, 或者$ t=\frac{k {\rm{ \mathsf{ π} }}}{\omega} $, k为整数, 则u_C=(－1)^kU_C0e^－δt, $-\delta t=-\delta \frac{k {\rm{ \mathsf{ π} }}}{\omega}=\frac{-k {\rm{ \mathsf{ π} }}}{\sqrt{m-1}} $。

由表 3可知, 衰减系数ω/ω_o反映一个振荡半周期时刻电压幅值的衰减程度; m值大于10后振荡角频率和无阻尼LC电路的振荡角频率比值接近1.0。

零输入响应电流最大值计算如下: 振荡电流获得最大值时, ωt_p=β, 或者$ t_{\mathrm{p}}=\frac{\beta}{\omega} $, $ \beta=\arctan \sqrt{m-1}, i_{\max }=\frac{U_{\mathrm{C} 0}}{\omega L} \mathrm{e}^{-\delta t} \sin \beta=\frac{U_{\mathrm{C} 0}}{\mathrm{Z}_0} \mathrm{e}^{-\delta t_{\mathrm{p}}} $, 而$-\delta t_{\mathrm{p}}=-\delta \frac{\beta}{\omega}=\frac{-\arctan \sqrt{m-1}}{\sqrt{m-1}} $。

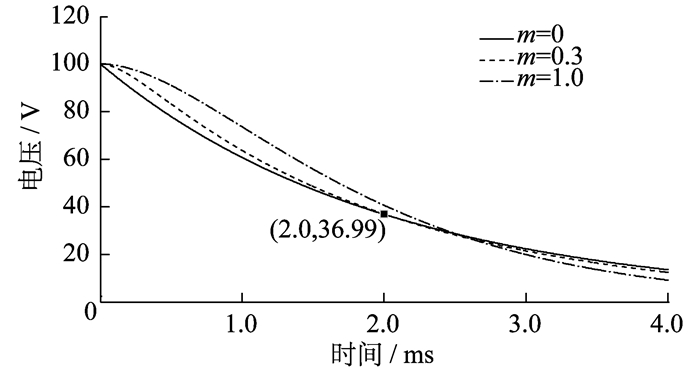
实例的参数如下: L=300 mH, R=2 kΩ, C=1.0 μF, U_C0=100 V; 则m=4L/R²C=0.3, $ k=r_2 /r_1=\frac{1+\sqrt{1-m}}{1-\sqrt{1-m}}=11.24 $, A₁=1.10U_C0, A₂=－0.10U_C0。设τ=RC=2 ms, 则－r₁τ=－K(m)=－1.09, 二阶RLC电路的零输入响应τ时刻的值和一阶RC电路的零输入响应τ时刻的值的比为u_C/u_RC=(A₁/U_C0)e^－r₁τ+1=1.005。

改变L使m=0.5, 则L=mR²C/4=500 mH, k=－A₁/A₂=r₂/r₁=5.8, 计算得A₁=1.21U_C0, A₂=－0.21U_C0, 则－r₁τ=－K(0.5)=－1.17, u_C/u_RC=(A₁/U_C0)e^－r₁τ+1=1.02。

上述计算表明, 振荡系数m为0.3和0.5时, τ=RC时刻二阶响应和一阶响应相近。改变L使m=1, 则L=mR²C/4=1 000 mH。改变L使m为零, 则L为零, 即二阶RLC电路变为一阶RC电路。利用MATLAB/Simulink进行仿真, 得到的非振荡二阶RLC电路仿真结果如图 2所示。

实例参数如下: 固定L=1.0 H, C=1.0 μF, U_C0=100 V, R选取3个不同值, 1 000 Ω, 200 $\sqrt{10}=632.4 \Omega, 200 \Omega $, 则对应m值为4, 10, 100。

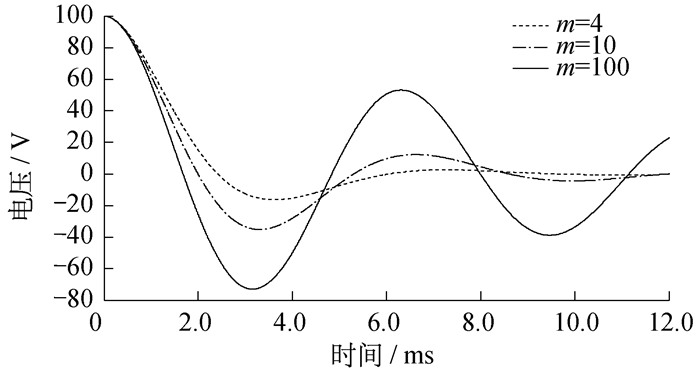
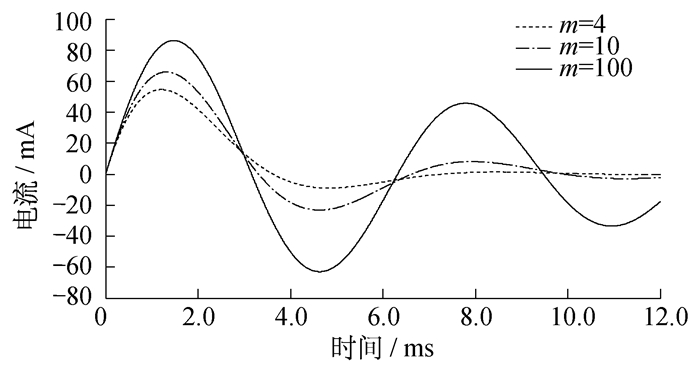
m=4时, 第1个振荡半周期时刻ωt=π时, $ -0.58 T_\omega=\frac{-{\rm{ \mathsf{ π} }}}{\sqrt{m-1}}=1.81 $, 则u_C=－U_C0e^－1.81=－16.5 V。零输入响应电流最大值β=1.05 rad, 则－δt_p=-0.604, 所以i_max=0.054 6 A。m=10时, 第1个振荡半周期时刻ωt=π时, $ -0.5 \delta T_\omega=\frac{-{\rm{ \mathsf{ π} }}}{\sqrt{m-1}}=-1.05 $, 则u_C=－U_C0e^－1.05=－35.0 V。零输入响应电流最大值β=1.25 rad, 则－δt_p=－0.417, 所以i_max=0.065 9 A。

m=100时, 第1个振荡半周期时刻ωt=π时, u_C=－U_C0e^－0.314=－73.0 V。零输入响应电流最大值β=1.47 rad, 则－δt_p=－0.148, 所以i_max=0.086 3 A。

利用MATLAB/Simulink进行仿真, 得到的暂态电压、电流波形图如图 3和图 4所示。由图 3和图 4可知, 振荡周期、暂态电流最大值出现时刻都与计算相符。

换流器电流不连续工况是高压直流输电的一种, 出现在启动投入运行过程的换流器单阀间歇性触发导通的暂态过程。系统交流电源经触发导通后的单阀接外部电路对换流器其他阀组件的相关RC回路电容充电。该暂态过程可等效为直流激励下的二阶RLC电路响应。对此进行计算可获得不导通阀的偏置电压。因为电路含有单向导通的晶闸管元件, 其过程仅延续半个振荡周期, 电流过零后阀截止即结束。

以一个典型的500 kV高压直流工程单阀触发的工况为例, 结合设备参数推算出二阶RLC电路参数, 进行直流激励下阶跃响应分析计算。当L=380.0 mH, C=18.0 nF, R=2.8 kΩ, 触发角为85°时的相电压瞬时值U_S=155.4 kV。直流激励下阶跃响应为$ u_{\mathrm{C}}=U_{\mathrm{S}}-\frac{U_{\mathrm{S}} \omega_0}{\omega} \mathrm{e}^{-\delta t} \sin (\omega t+\beta) $。计算得m=4L/R²C=10.8, 无阻尼振荡周期$ T_0=2 {\rm{ \mathsf{ π} }} \sqrt{L C}=0.52 \times 10^{-3} \mathrm{~s} $, 振荡周期$ T_\omega=\frac{\sqrt{m}}{\sqrt{m-1}} T_0=1.05 T_0=0.546 \mathrm{~ms} $, 振荡半周0.5T_ω=273.0 μs, 对应工频电角度为4.9°, 可见振荡半周期内工频电压值改变不大。半周衰减指数为$ \frac{-\delta T_\omega}{2}=\frac{-{\rm{ \mathsf{ π} }}}{\sqrt{m-1}}=-1.0 $, 第1个振荡半周期时刻ωt=π, u_C=U_S+U_Se^－δt=212.6 kV。

响应电流最大值β=1.26 rad, 则－δt_p=－0.403, 所以i_max=22.6 A。

本例的振荡系数m接近于10。由表 3可知, 当m值处于10附近时, 响应结果较适中, 即有一定的电流峰值和电压过冲值, 电流脉冲也得到一定程度的拓宽。这是高压直流输电系统在电流不连续工况下所期望的状态。实际的激励源是下降沿的工频正弦电压波, 在振荡半周内变化不大时可以近似为直流激励源。高压直流输电系统的电流不连续工况还有其他一些工作模式, 也可以近似为二阶RLC电路响应进行研究。

(1) 振荡系数m值小于等于0.3时, 二阶串联RLC电路的零输入响应近似等同于一阶RC电路的零输入响应。

(2) 利用振荡系数m可以得到振荡型暂态响应的简化计算公式。据此可以更直观地判断暂态响应结果与电路参数的关系。

(3) 利用MATLAB/Simulink进行了仿真, 验证了本文所提理论的正确性。

(4) 用所推导的方法对一个典型的500 kV高压直流工程在单阀触发工况下的实例二阶RLC电路进行了分析和计算, 暂态响应结果符合期望的状态。