|
|
|
发布时间: 2022-10-25 |
燃烧与污染物控制 |
|
|
|
收稿日期: 2022-04-02
基金项目: 国家自然科学基金(51906113)
中图法分类号: TK16
文献标识码: A
文章编号: 2096-8299(2022)05-0415-06
|
摘要
采用耦合误差传播和敏感性分析的直接关系图(DRGEPSA)法, 对甲烷燃烧详细反应机理(Gri-Mech 3.0机理)进行了简化, 构建出了一套含有23种组分和110步基元反应的简化机理。为验证该简化机理的合理性和可靠性, 采用充分搅拌反应器模型和一维层流预混反应器模型分别对甲烷燃烧反应过程进行模拟, 并对温度和组分摩尔分数分布进行了对比分析。结果显示: 利用简化机理分析得到的预测数据与详细机理吻合良好。结合该简化机理, 建立了二维数值模型对带伴流的甲烷/空气Flame D进行数值模拟仿真研究, 流场的温度和组分分布均与实验值吻合度较好, 进一步表明所提甲烷燃烧简化机理具有较高的模拟精度。
关键词
机理简化; 甲烷; 耦合误差传播和敏感性分析的直接关系图法; 燃烧数值模拟
Abstract
Direct Relation Graph with Error Propagation and Sensitivity Analysis (DRGEPSA) method coupled with error propagation and sensitivity analysis was used to simplify the detailed reaction mechanism of methane combustion (Gri-Mech 3. 0 mechanism), and a simplified mechanism containing 23 components and 110 step elementary reactions was constructed. In order to verify the rationality and reliability of the simplified mechanism, the fully stirred reactor model and one-dimensional laminar premixed reactor model were used to simulate the combustion reaction process of methane, and the temperature and mole fraction distribution of components were compared and analyzed. The results show that the combustion temperature and component volume fraction obtained by the simplified mechanism analysis are in good agreement with the detailed mechanism prediction data. Combined with the simplified chemical reaction mechanism, a two-dimensional numerical model is established to verify the numerical simulation of methane/air diffusion combustion (Flame D) with accompanying flow. The temperature and component distribution of the flow field are in good agreement with the experimental data, which further shows that the simplified mechanism of methane combustion obtained in this paper has high simulation accuracy and is suitable for numerical simulation of methane combustion.
Key words
simplified mechanism; methane; direct relation graph coupled with error propagation and sensitivity analysis; numerical simulation of combustion
甲烷(CH4)作为最简单的碳氢燃料, 广泛应用于各种动力设备和石化工业中。然而, CH4燃烧温度高, 导致热力型NOx的排放量较高[1]。近年来, 为了满足日趋严厉的环保标准, 降低燃气锅炉污染物的排放越来越受到研究人员的关注[2]。因此, 对燃烧过程中NOx含量的准确预测已成为目前研究的重点。当使用计算流体力学(Computational Fluid Dynanies, CFD)来预测燃烧温度和污染物的分布, 需要一个相对详细且准确的化学反应机理[3]。但是, 当详细化学反应机理直接在CFD模拟中耦合时, 会造成计算任务量过大[4]。同时, 详细机理中包含的多个时间尺度的反应往往会造成计算“刚性”问题[5], 导致求解效率较低。因此, 为了在满足一定计算精度的同时减少计算资源的消耗, 对化学反应机理进行简化具有重要意义。
前人针对CH4燃烧的详细机理进行了不同程度的简化。SUN J等人[6]得到了含有22种组分、65步基元反应的简化机理, 在较宽参数范围内的温度分布和NO分布与详细机理所得结果吻合较好, 其NO含量预测值误差小于2×10-6。MONNIER F等人[7]利用误差传播的直接关系图(Directed Relation Graph with Error Propagation, DRGEP)与Dijkstra搜索算法得到了含有17种组分、44步基元反应的简化机理, 该简化机理可大幅缩短计算时间。黄秋涵[8]得到了含有25种组分、96步基元反应的简化机理, 在不同CH4含量和当量比下均能准确预测火焰传播速度与点火延迟时间, 同时能准确展示CH4掺混燃烧时火焰形状。HU X Z等人[9]得到了含有20种组分、56步基元反应的简化机理, 对燃烧过程中的点火延迟时间和层流火焰速度的预测较好, 但无法对NO含量进行预测。
截至目前, 许多CH4燃烧简化机理中不包含NO生成反应[9-10], 无法对NO含量进行预测。为了获得适用于较大范围工况下CFD模拟的CH4燃烧简化机理, 并在准确预测温度分布和NO分布的同时减少对计算资源的消耗, 本文对CH4还原机理Gri-Mech 3.0(53种组分、325个基元反应)进行了简化, 得到了含有23种组分、110步基元反应的简化机理, 并通过Sandia Flame D模拟来验证该简化机理的合理性和可靠性。
1 CH4燃烧机理简化
1.1 简化方法
详细化学反应机理的简化主要通过剔除冗余的组分和基元反应实现。本文采用耦合误差传播和敏感性分析的直接关系图(Directed Relation Graph with Error Propagation and Sensitivity Analysis, DRGEPSA)法[11]对CH4燃烧的详细反应机理进行简化。DRGEPSA简化过程主要分为两个阶段: 第一阶段为DRGEP法; 第二阶段为敏感性分析(Sensitivity Analysis, SA)法。
第一阶段主要用于识别详细反应机理中冗余的组分与基元反应, 其中组分A对组分B的依赖强度反映其在整体中的产量或消耗量的占比, 用直接相互作用系数表示为
| $r_{\mathrm{AB}}=\frac{\left|\sum\limits_{i=1}^{n_{\mathrm{R}}}=v_{\mathrm{A}, i} \omega_i \delta_{\mathrm{B}}^i\right|}{\max \left|\sum\limits_{i=1}^{n_{\mathrm{R}}}=\max \left(0, v_{\mathrm{A}, i} \omega_i\right), \sum\limits_{i=1}^{n_{\mathrm{R}}}=\max \left(0, -v_{\mathrm{A}, i} \omega_i\right)\right|}$ | (1) |
式中: nR——总的基元反映数目;
υA, i——物种A在第i个基元反应中的化学计量数;
ωi——第i个基元反应的净反应速率;
δBi——第i个基元反应引入组分B后的误差,如果第i个基元反应包含组分B, 则其值为1, 否则为0。
组分A和B的反应路径的相互作用系数为
| $r_{\mathrm{AB}, \mathrm{P}}=\prod\limits_{j=1}^{n-1} r_{s_j s_{j+1}}$ | (2) |
式中: n——路径P中A和B之间的组分数目;
sj——A物种;
sj+1——B物种。
组分A和B的相互作用系数为
| $R_{\mathrm{AB}}=\max \left(r_{\mathrm{AB}, \mathrm{P}}\right)$ | (3) |
完成第一阶段后, 相互作用系数值大于εEP的组分以及涉及的基元反应被保留。此时进入第二阶段, 引入自定义敏感性分析阈值e*。当组分的相互作用系数值小于e*时, 对该组分以及涉及的基元反应计算其移除时的误差, 计算公式为
| $\delta_{\mathrm{B}}=\max \left|\delta_{\mathrm{B}, \text { ind }}-\delta_{\mathrm{DRGEP}}\right|$ | (4) |
式中: δB, ind, δDRGEP——详细机理和骨架机理中剔除组分B后引入的误差。
当δB低于误差阈值e*时, 组分B将被剔除。
1.2 简化机理
为了剔除详细机理中冗余的组分和基元反应, 需要建立反应器模型, 得到给定条件下的详细机理计算结果, 然后对结果进行分析。本文采用闭式均相反应器。计算过程所选取的样本点具体如表 1所示。
表 1
计算过程选取的样本点
| 样本点 | 温度T/K | 当量比φ |
| 1~30 | 1 000/1 200/1 400/1 600/1 800/2 000 | 0.6/0.8/1.0/1.2/1.4 |
简化过程中首先要确定目标组分。目前为止目标组分的确定尚未有统一的准则, 只能依靠经验进行选取。本文选取CH4, O2, CO2, CO, H2O, NO为目标组分, 目标参数的相对误差设置为10%, 阈值设置为1×10-6。
采用上述DRGEPSA法简化后, 含有53种组分、325步基元反应的Gri-Mech 3.0机理被简化为一套包含23种组分、110步基元反应的简化机理。
2 CH4燃烧简化机理验证
为了验证简化机理的准确性, 基于充分搅拌反应器和一维层流预混反应器模型, 将简化机理与详细机理预测所得结果进行对比。
2.1 充分搅拌反应器模型验证
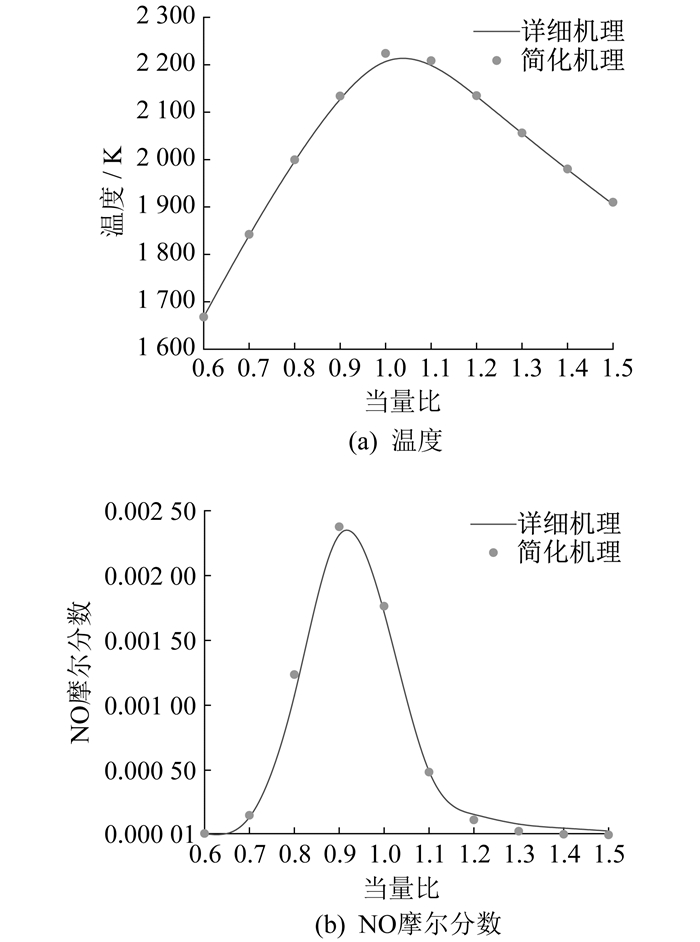
反应器容积设置为10 cm3, 气体停留时间为2 s, 初始温度为1 200 K, 燃料流率为0.04 g/cm·s。充分搅拌反应器中简化机理和详细机理预测结果对比如图 1所示。
由图 1(a)可知: 当量比从0.6增大到1.0时, 温度从1 680 K增大到2 250 K; 而当量比进一步从1.0增大到1.5时, 温度从2 250 K减小到1 900 K。这是因为随着当量比的增加, 反应过程逐渐由富燃状态向贫燃状态转变。当量比等于1.0时, 燃料/空气浓度处于化学当量比下, 燃烧反应释放的热量最多, 而当量比大于1.0时, 多余的空气吸收部分热量, 导致温度逐渐下降。由图 1(b)可知: 简化机理与详细机理预测所得NO摩尔分数分布趋势十分相似, 但简化机理的NO摩尔分数峰值比详细机理所得结果略高; 当量比大于1.0时, 随着当量比逐渐增大, 反应温度逐渐降低, NO摩尔分数随之下降。总体来说, 简化机理与详细机理的预测结果误差较小,简化机理能较为准确地预测当量比在0.6~1.5范围内的温度分布与NO分布。
2.2 一维层流预混反应器模型验证
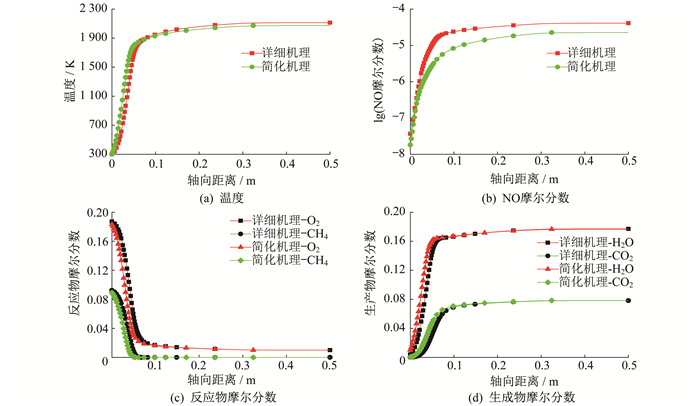
在一维层流预混反应器模型中, 初始时温度设置为300 K, 气压为1.013 25×105 Pa, 化学反应当量比为1.0, 最终状态时CH4完全燃烧, 生成CO2和H2O。轴向距离为0.5 cm, 入口气体质量流率为0.04 g/cm·s。一维层流预混反应器中简化机理预测结果对比如图 2所示。
由图 2可知: 随着轴向距离的增大, 温度迅速由300 K升高到1 900 K, 随后基本保持不变; NO摩尔分数分布趋势与温度分布趋势基本一致, 均在较短距离内达到峰值后趋于稳定; 在温度达到最大值时, NO摩尔分数也达到最大值, 表明CH4燃烧过程中产生的NOx主要为热力型NOx; 在轴线方向上, 反应物浓度逐渐降低, 生成物浓度逐渐增大。由组分分布可以看出, 甲烷迅速反应完全, 这与温度分布趋势基本吻合。简化机理预测所得温度分布和组分分布与详细机理预测所得结果吻合较好, NO含量预测结果在轴向距离大于0.05 m时存在一定偏差。
3 CH4燃烧简化机理在CFD模拟中的应用
3.1 模拟设置
模拟过程中压力-速度的耦合采用Coupled算法, 利用二阶迎风格式离散各基本方程。能量方程的收敛标准设置为10-6, 其他方程的收敛标准为10-3, 时间步长设置为1×10-6 s。
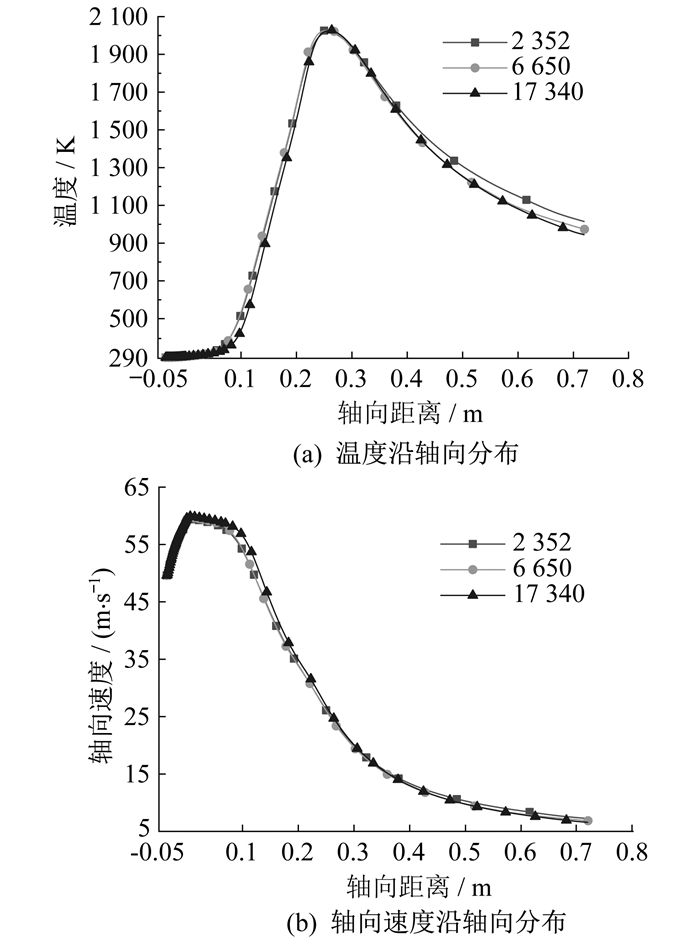
3.2 网格无关性验证
3.3 模拟结果讨论
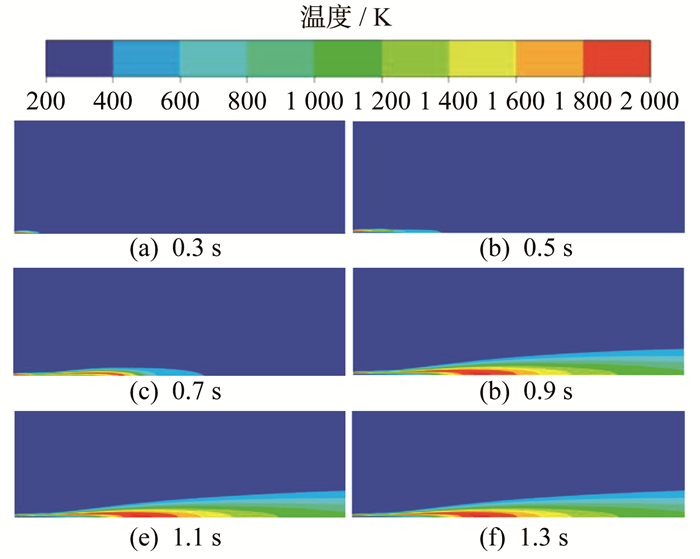
燃烧器内温度分布随时间变化情况如图 4所示。
由图 4可知, 在0.9~1.1 s内, 温度场分布未有明显变化, 表明反应在0.9 s后达到稳定状态。
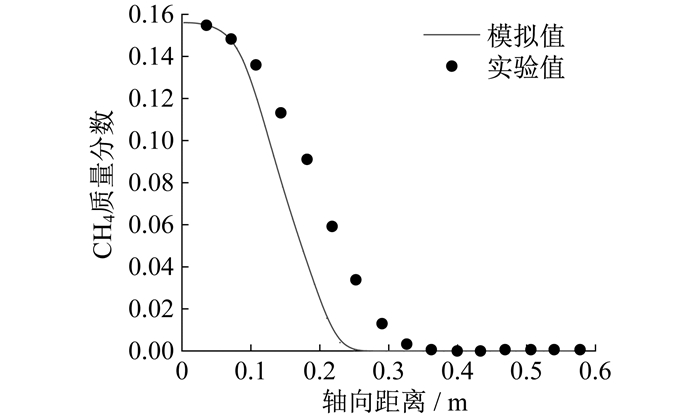
简化机理预测所得CH4质量分数模拟值与实验值的对比如图 5所示。
由图 5可知: CH4质量分数的模拟值与实验值在反应开始与结束区域吻合较好; 在CH4燃烧反应区域, 模拟中CH4消耗速率更快; 另外, 模拟中CH4反应区域在轴向距离0.03~0.25 m, 而实验中CH4反应区域在0.03~0.30 m。
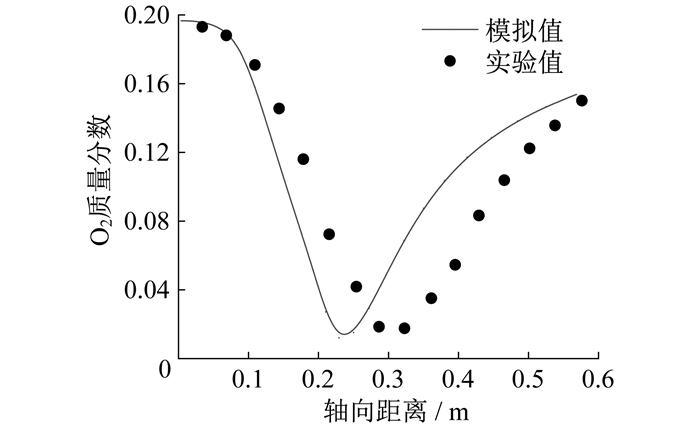
简化机理预测所得O2质量分数模拟值与实验值的对比如图 6所示。
由图 6可知: 模拟燃烧反应中O2质量分数最小值略低于实验值, 相对误差为3.1%;在轴向距离小于0.3 m范围内, 实验中的O2质量分数略高于模拟值, 可见与CH4质量分数在轴向距离小于0.3 m范围内的分布规律相一致; 与实验相比, 模拟中O2消耗速率更快。
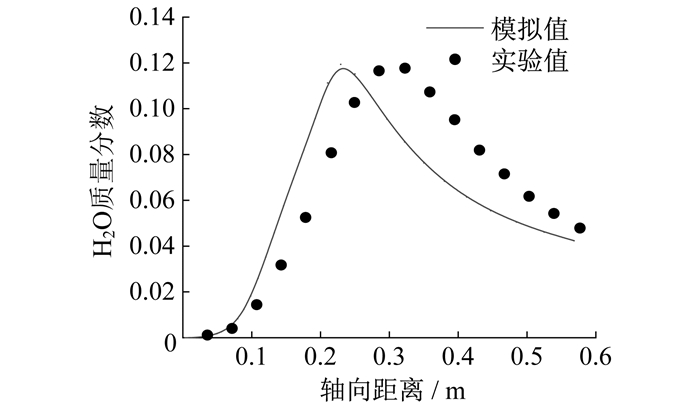
简化机理预测所得H2O质量分数模拟值与实验值的对比如图 7所示。
由图 7可知: H2O呈现先上升后下降的分布趋势; H2O质量分数的模拟峰值比实际值略高, 相对误差约为1.5%, 峰值位置前移约0.1 m。
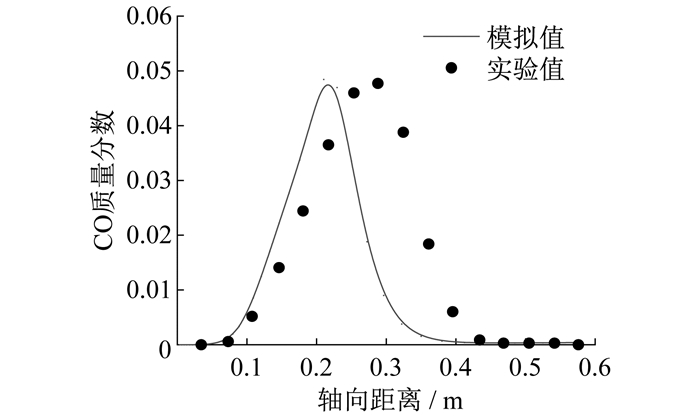
简化机理预测所得CO质量分数模拟值与实验值的对比如图 8所示。
由图 8可知: CO质量分数的模拟峰值比实际值略高, 相对误差约为1.5%, 峰值位置前移约0.08 m是由于前期CH4燃烧反应快速, 氧气供应不足所导致; 随着轴向距离进一步增加, 氧气含量增加, CO含量逐渐降低, 在轴向距离为0.4 m时, CO含量降至零。
对比图 5~图 8中的数据可知, 曲线在到达峰值前, 其上升/下降的速度比实际燃烧反应要快, 是因为在模拟燃烧反应时, 燃料点火时间要早于实际燃烧着火时间, 就导致模拟时燃烧反应速率更快, 与实际燃烧峰值出现偏差。同时, 实际燃烧使用的燃料与模拟时燃料设置有一定的差别, 也会造成模拟的组分分布与实验有些差别。总体而言, 基于简化机理对CH4/空气Flame D预测所得结果与实验结果吻合较好, 证明了本文所得简化机理在CH4燃烧模拟中应用的可行性。
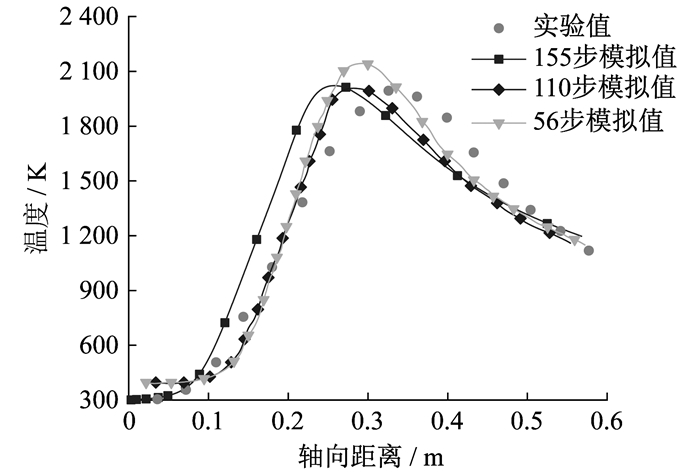
为了进一步验证该简化机理的准确性, 选择文献[9](56步)、文献[10] (155步)以及本文提出的CH4燃烧简化机理模型(110步)对Sandia Flame D进行模拟。各简化机理预测所得温度与实验值的对比如图 9所示。
由图 9可知: 相对于其他两个简化机理, 本文所提出的简化机理对温度的预测效果较好, 56步机理模拟值与实验偏差最大, 最大误差为8.5%;本文提出简化机理模拟的最高温度与实验值较为接近, 均在1 900~2 000 K范围内, 但最高温度模拟值比实验值高约为38 K, 相对误差为2%。
4 结语
本文采用DRGEPSA法对CH4燃烧详细机理(Gri-Mech 3.0机理)进行简化, 得到了包含23种组分和110步基元反应的简化机理, 并通过充分搅拌反应器模型和一维层流预混反应器模型验证了该简化机理的合理性。
结合简化机理, 对美国Sandia国家实验室经典湍流射流火焰中的CH4/空气Flame D进行了二维数值模拟, 得到了CH4, O2, CO2, CO等组分在燃烧器内的分布, 模拟结果与实验结果吻合良好, 进一步证明了该简化机理的可靠性。
在本文简化机理过程中, 重点关注简化机理对燃烧特性预测的误差。如对简化过程中反应动力学信息考虑不足, 可能会导致某些反应过程被加强或减弱。后期可使用多种简化方法, 同时考虑简化过程中的动力学问题, 进一步提高简化机理精度。
参考文献
-
[1]靳苏毅, 王登辉, 惠世恩, 等. 天然气低氮氧化物燃烧研究进展与展望[J]. 节能技术, 2021(4): 291-298.
-
[2]SHI B L, HU J, PENG H W, et al. Effects of internal flue gas recirculation rate on the NOx emission in a methane/air premixed flame[J]. Combustion and Flame, 2018, 188: 199-211. DOI:10.1016/j.combustflame.2017.09.043
-
[3]肖民, 黄志伟, 刘玉坪, 等. 基于化学反应动力学的双燃料发动机数值模拟[J]. 船舶工程, 2021, 43(8): 63-72.
-
[4]XIAO H, WANG Z, AGUSTIN V M, et al. Study on characteristics of co-firing ammonia/methane fuels under oxygen enriched combustion conditions[J]. Journal of Thermal Science, 2018, 27(3): 270-276. DOI:10.1007/s11630-018-1008-1
-
[5]孙继昊. 甲烷/空气机理简化及燃烧室污染物空间分布[D]. 哈尔滨: 哈尔滨工程大学, 2020.
-
[6]SUN J, ZHANG Z, LIU X, et al. Reduced methane combustion mechanism and verification, validation, and accreditation (VV&A) in CFD for NO emission prediction[J]. Thermal Science, 2021, 30(2): 14.
-
[7]MONNIER F, RIBERT G. Simulation of high-pressure methane-oxygen combustion with a new reduced chemical mechanism combustion and flame[J]. Journals & Books, 2022, 235: 111735.
-
[8]黄秋涵. 微尺度条件下CH4/DME掺混燃料燃烧过程反应机理简化及数值模拟研究[D]. 镇江: 江苏大学, 2020.
-
[9]HU X Z, YU Q B, LI Y X, et al. A minimal skeletal mechanism for combustion of CH4/O2/CO2 mixtures[J]. Energy & Fuels, 2016, 30(2): 1407-1414.
-
[10]CHEN Y, CHEN J Y. Towards improved automatic chemical kinetic model reduction regarding ignition delays and flame speeds[J]. Combustion and Flame, 2018, 190: 293-301. DOI:10.1016/j.combustflame.2017.11.024
-
[11]LI Y Q, CHEN Y, WU G. A new skeletal mechanism for diesel-n-butanol blends combustion in engine[J]. Fuel, 2020, 264: 116856. DOI:10.1016/j.fuel.2019.116856
-
[12]袁琪. 某型低氮燃烧器的结构设计和数值模拟[D]. 岳阳: 湖南理工学院, 2021.
-
[13]吴校宇. 燃煤锅炉二次风分配特性的数值模拟[D]. 北京: 华北电力大学, 2021.
-
[14]DUAN Y F, XIA Z X, MA L K, et al. Numerical simulation of the Sandia Flame D using the ESF method coupled with FGM model[J]. Cluster Computing, 2019, 22: 15130-15110.
-
[15]解俊良. 低NOx天然气燃烧器的设计与数值模拟[D]. 北京: 北京交通大学, 2020.
-
[16]BERTELS A, KOBER B, RITTLER A, et al. Large-eddy simulation of Sandia Flame D with efficient explicit filtering[J]. Flow, Turbulence and Combustion, 2019, 102: 887-907.
-
[17]MIRANDA F C, COELHO P J, MARE F D, et al. Study of turbulence-radiation interactions in large-eddy simulation of scaled Sandia Flame D[J]. Journal of Quantitative Spectroscopy and Radiative Transfer, 2019, 228: 47-56.
-
[18]董良. 甲烷扩散火焰燃烧与重整的数值模拟[D]. 上海: 华东理工大学, 2011.