|
|
|
发布时间: 2023-02-28 |
清洁安全发电 |
|
|
|
收稿日期: 2022-10-19
基金项目: 上海市"科技创新行动计划"地方院校能力建设专项项目(19020500700)
中图法分类号: TK472
文献标识码: A
文章编号: 2096-8299(2023)01-0019-06
|
摘要
为防止电站燃气轮机燃烧室在工作期间出现故障而导致重大经济损失, 提出了一种基于灰色关联度分析和深度自回归模型(GRA-DeepAR)的故障预警方法。首先, 采集燃气轮机的正常运行数据进行GRA, 提取出与透平排气温度高度相关的特征参数; 然后, 采用DeepAR对透平排气温度进行预测, 并设定预警阈值, 以此建立深度自回归故障预警模型; 最后, 根据残差绝对值是否超过预警线来间接判断燃烧室的运行情况。以某电厂安萨尔多燃气轮机的运行数据为例进行了分析, 结果表明: 该方法能够提前识别燃烧室的异常状况, 同时发出预警信号提醒工作人员进行处理, 可为燃气轮机燃烧室故障预警提供实际参考。
关键词
燃气轮机; 燃烧室; 故障预警; 灰色关联度分析; 深度自回归模型
Abstract
In order to prevent the major economic losses caused by the failure of the gas turbine combustion chamber in the power plant during the working period, a fault early warning method based on Grey Relation Analysis-Deep Autoregressive Model (GRA-DeepAR) is proposed.Firstly, the normal operation data of the gas turbine are collected for GRA, and the characteristic parameters highly related to the turbine exhaust temperature are extracted; Then, DeepAR is used to predict the turbine exhaust temperature, and an early warning threshold is set to establish a deep autoregressive fault early warning model; Finally, the operation of the combustion chamber is judged indirectly according to whether the absolute value of the residual exceeds the warning line.Taking the operation data of Ansaldo gas turbine in a power plant as an example, the results show that the method can identify the abnormal conditions of the combustion chamber in advance, and send an early warning signal to remind the staff to deal with them, providing practical reference for the early warning of gas turbine combustion chamber failure.
Key words
gas turbine combustion chamber; fault early warning; grey relational analysis; deep autoregressive model;
燃气轮机是燃气-蒸汽联合循环机组的核心动力装备。它由压气机、燃烧室和透平3大部分组成, 其中燃烧室被称作燃气轮机的心脏, 燃烧室工作运行的可靠性将直接影响到燃气轮机工作运行的可靠性[1]。燃烧室长期在高温高压的恶劣环境下运行, 随着运行时间的增加, 内部可能会发生喷嘴堵塞和火焰筒变形、破裂等故障[2], 将阻碍燃气轮机的正常运行, 甚至会造成严重事故。如果能在早期发现燃烧室的异常情况, 及时给出维护建议, 可以降低由这些故障引起的机组安全事故或非计划停机的风险[3], 并大大提高燃气轮机的稳定性和经济性。
近年来, 人工智能和深度学习不断普及到各个领域, 为燃气轮机燃烧室故障预警提供了新的思路。叶家豪等人[4]利用灰色关联分析(Grey Relation Analysis, GRA)建立了训练样本集, 提高了历史数据与预测日时间尺度上的信息关联度。黄伟、张泽发[5]通过构建燃烧室的多元状态估计模型, 引用相似性对真实值和预测值的相似程度进行衡量, 用以判断燃烧室的运行情况, 虽然能进行故障预警, 但预警时间不够提前。彭道刚等人[6]采用长短期记忆网络(Long Short Term Memory, LSTM)对燃气轮机压气机进行了故障预警, 可以有效预警, 但需要庞大的数据集进行分析。SALINAS D等人[7]提出了一种产生精确点预测和概率预测的深度自回归模型(Deep Autoregressive Model, DeepAR), 是基于对大量相关时间序列训练的一个自回归的递归网络模型, 并通过对几个真实的预测数据集进行广泛的实证评估, 与常用循环神经网络(Recurrent Neural Networks, RNN)方法相比, 精度有所提高, 但该方法没有用于燃气轮机燃烧室方向的研究。
针对燃烧室故障预警的现状和存在的问题, 本文提出了一种基于灰色关联度分析和深度自回归模型(Grey Relation Analysis-Deep Autoregressive Model, GRA-DeepAR)的燃气轮机燃烧室故障预警方法。利用GRA对正常运行的燃气轮机数据进行分析, 温度特征可以有效反映燃烧室故障的渐变趋势。但由于燃烧室内部的火焰温度很高, 如果安装温度传感器进行测量, 会导致传感器直接损坏。现阶段的方法一般是采取测量透平排气温度间接反馈燃烧室的工作变化趋势[8]。本文通过提取与透平排气温度关联度高的特征参数作为DeepAR预测模型的输入, 计算得到温度实际值与预测值之间的残差绝对值, 并用概率分布拟合设定预警阈值, 进而实现燃气轮机燃烧室的故障预警。
1 相关理论研究
1.1 DeepAR模型
DeepAR是一种基于深度学习的时间序列预测方法。燃气轮机的数据是按照时间周期进行采样的, 且采样时间固定, 这符合DeepAR模型的实行标准。DeepAR由RNN (LSTM)组成内部架构, 作为一种监督学习算法, 能够在一定程度上减轻对数据的要求, 也克服了LSTM模型的不足; 同时, 可以有效地从相关的时间序列中学习全局模型及复杂模式, 从而对时间序列进行预测[9]。
DeepAR的目标是对条件概率分布进行建模, 即给定过去时间序列[zi, 1, …, zi, t0-2, zi, t0-1]=Zi, t0-1和协变量Xi, 1∶T, 建立每个未来时间序列[zi, t0, zi, t0+1, …, zi, T]=Zi, t0∶T的条件概率分布
| $ P\left(Z_{i, t_0: T} \mid Z_{i, 1: t_0-1}, X_{i, 1: T}\right) $ | (1) |
式中: Zi, t——时间序列i在时间t处的值;
t0——时间划分点。
假设模型分布为QΘ(Zi, t0∶T∣Zi, 1∶t0-1, Xi, 1∶T), 则其可以转化为以下的似然形式, 即
| $ \begin{gathered} Q_{\mathit{\Theta}}\left(Z_{i, t_0 : T} \mid Z_{i, 1: t_0-1}, X_{i, 1: T}\right)=\prod\limits_{t=t_0}^T Q_{\mathit{\Theta}}\left(z_{i, t} \mid Z_{i, 1: t-1}, X_{i, 1: T}\right)= \\ \prod\limits_{t=t_0}^T l\left(z_{i, t} \mid \theta\left(h_{i, t}, \mathit{\Theta}\right)\right) \end{gathered} $ | (2) |
| $ h_{i, t}=H\left(h_{i, t-1}, z_{i, t-1}, X_{i, t}, \mathit{\Theta}\right) $ | (3) |
式中: l——似然函数;
θ——似然函数l的参数;
Θ——网络结构参数;
hi, t——隐藏层输出;
H——包含LSTM的多层循环网络。
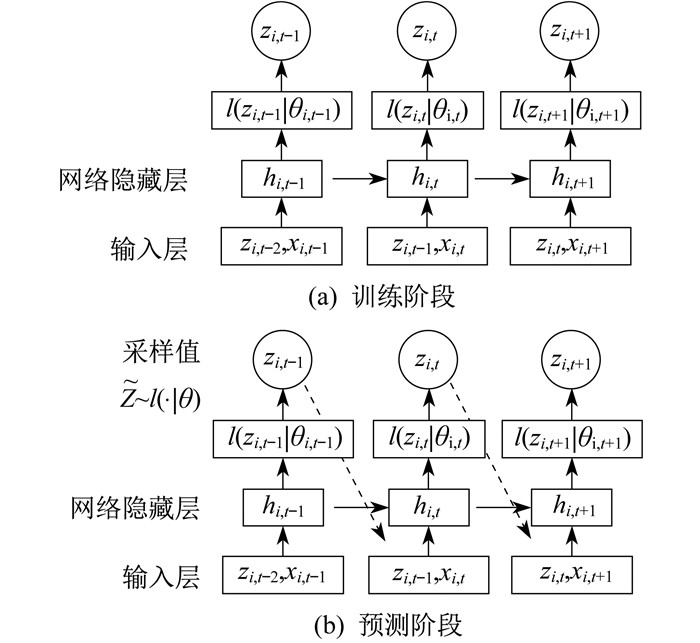
DeepAR模型是自回归循环网络(Autoregressive Recurrent Network, ARN)结构, 如图 1所示。
在训练阶段, DeepAR输入上一时间的隐藏层hi, t-1、目标值Zi, t-1以及当前时间的协变量Xi, t和模型参数Θ, 就能得到当前时间的隐藏层输出hi, t, 从而计算似然函数l(Z|θ)的参数θi, t=θ(hi, t, Θ), 最后通过对数似然概率最大化来学习得出最佳模型参数Θ。
| $ L=\sum\limits_{i=1}^N \sum\limits_{t=t_0}^T \log l\left(z_{i, t} \mid \theta\left(h_{i, t}\right)\right) $ | (4) |
式中: L——对数似然函数;
T——采样时间。
在预测阶段, 每个时间点t运用蒙特卡洛采样得到
θ的形式取决于似然函数l的形式, 因为燃气轮机监测数据为实值数据, 服从高斯分布, 所以似然函数形式为
| $ l_{\mathrm{G}}\left(Z_{i, t} \mid \mu, \sigma\right)=\left(2 \pi \sigma^2\right)^{-\frac{1}{2}} \exp \frac{-\left(Z_{i, t}-\mu\right)^2}{2 \sigma^2} $ | (5) |
| $ \mu\left(h_{i, t}\right)=\boldsymbol{W}_\mu^{\mathrm{T}} h_{i, t}+\boldsymbol{b}_\mu $ | (6) |
| $ \sigma\left(h_{i, t}\right)=\log \left(1+\exp \left(\boldsymbol{W}_\sigma^{\mathrm{T}} h_{i, t}+\boldsymbol{b}_\sigma\right)\right) $ | (7) |
式中: μ——均值;
σ——标准差;
μ(hi, t)——高斯分布函数的均值;
Wμ、Wσ——权重矩阵;
bμ、bσ——偏置矩阵;
σ(hi, t)——高斯分布函数的标准差。
从理论上来说, DeepAR模型具有较好的预测效果。但, 燃气轮机燃烧室结构复杂, 特征参数多, 且特征参数之间的关联性很强, 增加了故障预警的难度, 因此需要对特征参数作进一步处理。
1.2 灰色关联度分析
通常来说, 对正常运行的燃气轮机燃烧室进行预测时, 应该尽可能多地选取输入特征参数, 但这样不仅会增大预测时的工作量, 而且较多的特征参数可能会相互重叠, 反映相似的信息, 使得预测没有客观性。
对于上述问题, 大多数学者一般会使用主成分分析(Principal Component Analysis, PCA)将高维的状态变量转换为低维的变量[10]。但PCA具有局限性, 被原始变量所限制, 在降维时容易丢失重要信息; 而GRA可以克服PCA的不足, 能显示出变量之间的特征以及动态关联程度。因此, 本文采用GRA进行特征参数的提取, 降低预测工作量。
GRA是一种针对多因素统计和分析的方法, 可以分析向量之间、矩阵之间的关联度, 或计算得出预测序列与比较特征序列之间的相关程度[11]。
假设预测序列为
| $ X_0=\left(x_0(1), x_0(2), x_0(3), \cdots, x_0(n)\right) $ | (8) |
m个比较特征序列为
| $ \begin{gathered} X_i=\left(x_i(1), x_i(2), x_i(3), \cdots, x_i(n)\right) \\ i=1, 2, 3, \cdots, m \end{gathered} $ | (9) |
则两个序列之间的关联度系数为
| $ \begin{aligned} & \zeta_i(k)= \\ & \frac{\min\limits_i \min\limits_k\left|X_0(k)-X_i(k)\right|+\rho \max\limits_i \max\limits_k\left|X_0(k)-X_i(k)\right|}{\left|X_0(k)-X_i(k)\right|+\rho \max\limits_i \max\limits_k\left|X_0(k)-X_i(k)\right|} \\ & k=1, 2, 3, \cdots, n \\ & \end{aligned} $ | (10) |
式中:
ρ——分辨率系数, 通常在[0, 1]之间。
X0与Xi之间的关联度为
| $ \gamma\left(X_0, X_i\right)=\frac{1}{n} \sum\limits_{k=1}^n \zeta_i(k) $ | (11) |
2 燃气轮机燃烧室故障预警
燃气轮机燃烧室故障的产生会有早期的预兆。这些预兆体现在燃气轮机运行参数的变化中。通过提取特征参数, 建立预测模型, 监测真实值与模型预测值的残差绝对值曲线, 以捕获故障发展趋势, 从而实现燃气轮机燃烧室的故障预警。
2.1 燃烧室常见故障
2.2 故障预警流程
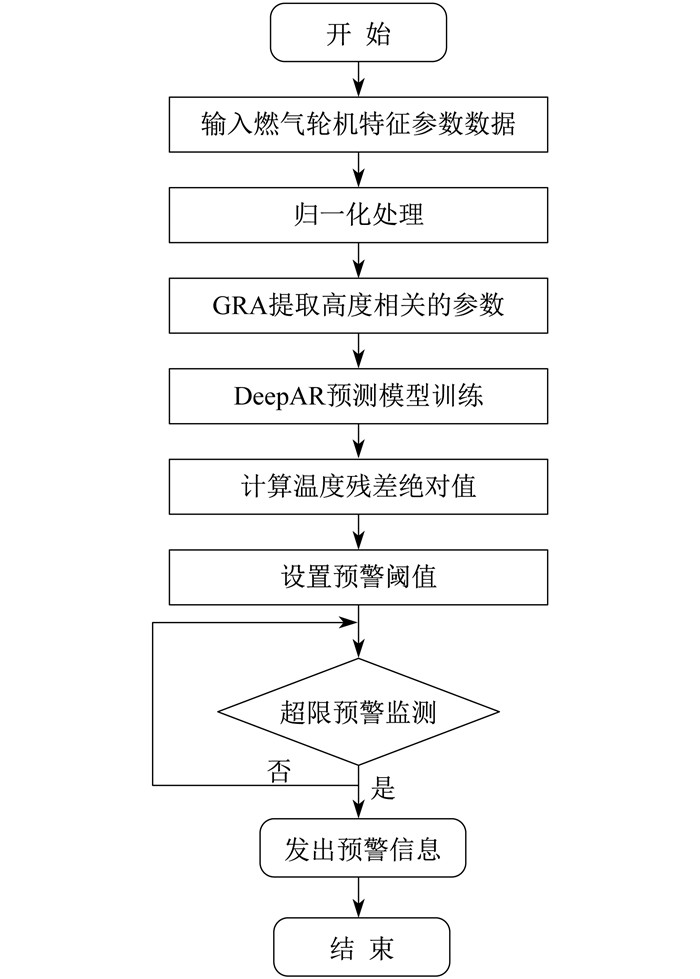
首先对正常历史数据进行归一化处理, 提取出与透平排气温度高度相关的特征参数; 其次对DeepAR模型进行训练, 使其具有可观的预测效果; 最后将待测的数据输入到训练完成的模型中, 对透平排气温度的残差绝对值进行监测, 并设置预警阈值, 若超过阈值的限定范围则发出预警信息。
故障预警流程如图 2所示。
2.3 特征参数选取
预测透平排气温度, 需要融合燃气轮机中的多种监测信息。燃气轮机运行过程中, 工作状况时有变化, 本文根据相关经验[8], 和燃气轮机操作台的仿真分析, 研究测点排温与其他参数的变化情况, 选取其中与透平排气温度相关的17个参数进行分析处理。
采用灰色关联度分析, 选择透平排气温度为预测序列, 其余17个特征参数为比较特征序列, 经过归一化处理后, 根据式(8)~式(11)计算预测序列与比较特征序列之间的灰色关联度, 并对17个参数的关联度从大到小进行排序, 结果如表 1所示。
表 1
透平排气温度与各特征参数的灰色关联度
| 特征参数 | 关联度 | 特征参数 | 关联度 | |
| 火检信号1 | 0.749 6 | 燃气进口温度 | 0.602 4 | |
| 火检信号2 | 0.733 2 | 控制信号输出 | 0.569 1 | |
| 进气导流叶片 | 0.721 3 | 压气机出口温度 | 0.561 1 | |
| 火检信号3 | 0.673 9 | 平均排气温度 | 0.558 9 | |
| 燃烧室压力 | 0.645 9 | 透平末级叶片温度 | 0.546 7 | |
| 火检信号4 | 0.645 1 | 叶片通道平均温度 | 0.536 9 | |
| 旁路阀开度 | 0.643 4 | 燃气透平膨胀比 | 0.534 9 | |
| 燃气轮机功率 | 0.621 1 | 燃气透平效率 | 0.532 6 | |
| 燃料流量 | 0.611 9 |
由灰色理论可知: 灰色关联度越大, 则此特征参数对透平排气温度的影响越大; 反之, 对其影响越小。根据相关文献经验[14], 可以忽略灰色关联度较小的参数。考虑到后续预测模型建立问题, 本文选取灰色关联度大于0.6的10个特征参数作为透平排气温度预测模型的输入。
2.4 预警阈值设置
燃气轮机燃烧室正常工作时, 透平排气温度的真实值与预测值的残差绝对值较小; 当燃烧室出现异常情况时, 残差绝对值就会偏离正常区间。随着运行时间的增加, 异常状况加剧, 残差绝对值会出现明显变化。由上述分析可知, 燃烧室是否出现异常可以通过监测透平排气温度的残差绝对值是否超过预警阈值来确定。
通过拟合燃烧室正常工作的透平排气温度残差绝对值, 得到相应的概率密度函数f(E), 则预警阈值V可以由式(12)得出[15], 即
| $ \int_{\mathrm{V}}^{+\infty} f(E) \mathrm{d} E=\alpha, \quad 0<\alpha<1 $ | (12) |
式中: E——残差绝对值;
α—显著性水平。
为排除一些特定干扰, 选取α=0.05。当E<V时, 燃烧室运行正常; 当E>V时, 燃烧室发生异常情况。
2.5 预测模型评价指标
通常采用3个评价指标来反映模型的预测效果, 即平均绝对误差MAE, 均方根误差RMSE, 拟合优度R2[15]。
| $ \text { MAE }=\frac{1}{n} \sum\limits_{i=1}^n\left|y(i)-y^{\prime}(i)\right| $ | (13) |
| $ \operatorname{RMSE}=\sqrt{\frac{1}{n} \sum\limits_{i=1}^n\left(y(i)-y^{\prime}(i)\right)^2} $ | (14) |
| $ R^2=1-\frac{\sum\limits_{i=1}^n\left[y(i)-y^{\prime}(i)\right]^2}{\sum\limits_{i=1}^n[y(i)-\bar{y}(i)]^2} $ | (15) |
式中: y(i)——第i个时间的温度真实值;
y′(i)——第i个时间的温度预测值;
y(i)——第i个时间的温度平均值。
预测的偏差越小, 则MAE越小; 预测的结果越精确, 则RMSE越小; 曲线的拟合度越好, 则R2越接近1。
3 实验及结果分析
3.1 正常运行下模型预测分析
选取国内某电厂安萨尔多燃气轮机的1期运行数据进行分析。该燃气轮机的采样频率为1次/min, 用燃气轮机正常运行的9 000组数据作为训练集, 500组数据作为测试集, 并为DeepAR模型设置合适的模型参数。经过多次迭代训
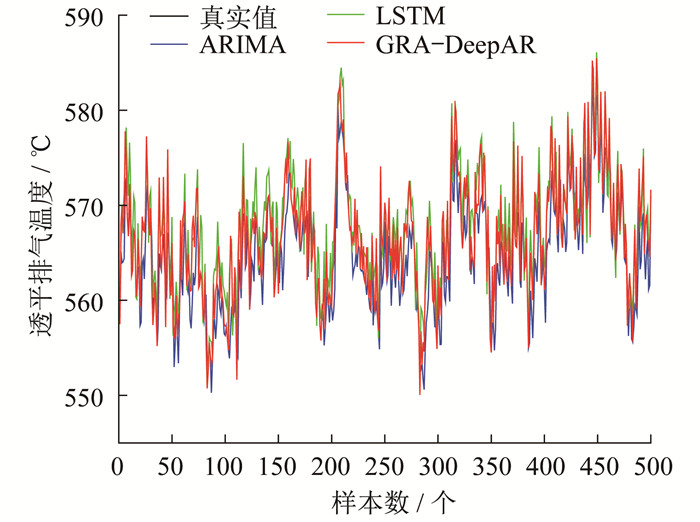
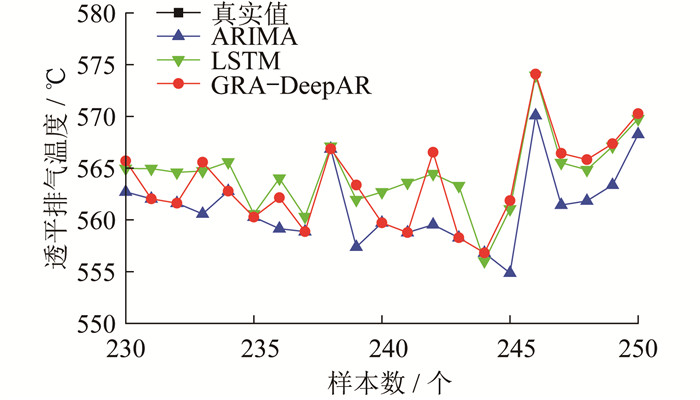
练后, 用训练好的模型对测试集进行预测验证, 同时与整合移动平均自回归模型(Autoregressive Integrated Moving Average Model, ARIMA模型)和LSTM模型两种经典时间序列预测模型进行比较。不同模型的预测曲线如图 3和图 4所示。
由图 3和图 4可知, GRA-DeepAR模型的预测效果优于ARIMA模型和LSTM模型。
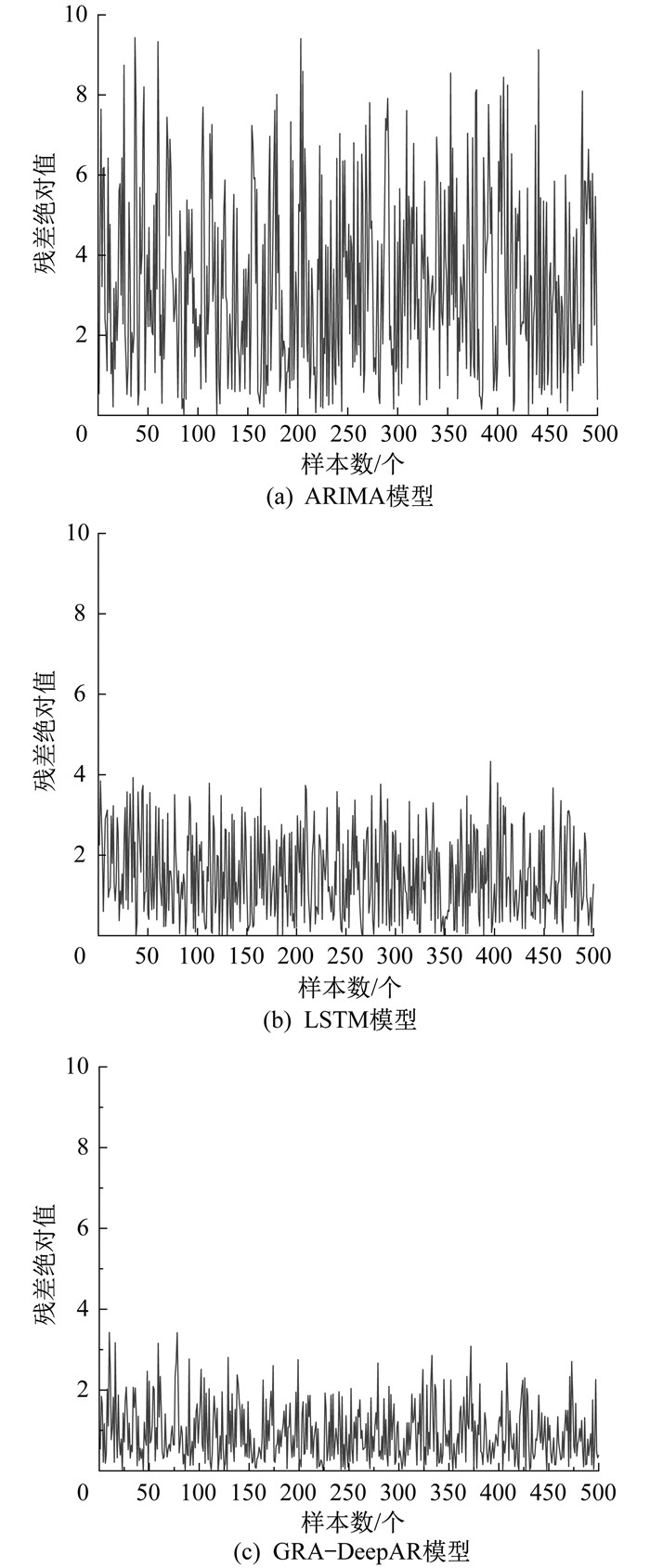
通过残差绝对值的计算可以更好地体现对比。3种预测模型的残差绝对值如图 5所示。
由图 5可以明显看出, GRA-DeepAR预测模型的残差绝对值比其他两种模型要低。
通过3种常规的评价指标来反映3种模型的预测效果, 其分析结果如表 2所示。
表 2
3种预测模型的误差分析结果
| 预测模型 | 评价指标 | ||
| MAE | RMSE | R2 | |
| ARIMA | 3.302 9 | 3.990 8 | 0.599 8 |
| LSTM | 1.496 5 | 1.827 3 | 0.916 1 |
| GRA-DeepAR | 0.935 1 | 1.177 3 | 0.965 2 |
由表 2可知: GRA-DeepAR模型的MAE为0.935 1, 与ARIMA和LSTM模型相比分别降低了2.367 8和0.561 4;GRA-DeepAR模型的RMSE为1.177 3, 与ARIMA和LSTM模型相比分别降低了2.813 5和0.650 0;GRA-DeepAR模型的R2为0.9652, 与ARIMA和LSTM模型相比分别提升了0.365 4和0.049 1。由此表明, 本文所提的GRA-DeepAR预测模型精度更高, 可以进行故障预警。
3.2 故障预警分析
将上述计算获得的燃烧室正常运行时的透平排气温度残差绝对值进行概率分布拟合, 拟合结果服从对数正态分布。密度函数为
| $ f(E, \mu, \sigma)=\frac{1}{E \sigma \sqrt{2 \pi}} \mathrm{e}^{-\frac{(\ln E-\mu)^2}{2 \sigma^2}} $ | (16) |
通过拟合得出的μ=-0.493 9, σ=1.158 87。将式(16)代入式(12), 即可求得预警阈值V=5.064 1。预警阈值设置完成后, 即可进行故障预警分析。
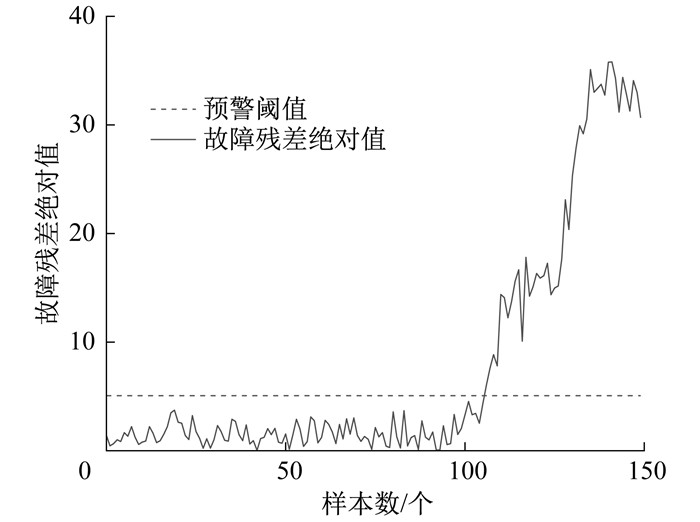
已知某电厂安萨尔多燃气轮机燃烧室在某一时间出现喷嘴积碳, 在此故障隐患下经过一段时间的运行后, 出现燃烧异常, 最终导致燃烧室熄火停止运行。为验证本文所提方法的有效性, 选取上述故障发生前的正常运行历史数据5 000组作为训练集, 故障发生前夕以及发生故障之后的500组数据作为预测集, 得出其残差绝对值后提取出故障发生前夕片段进行分析。图 6为故障预警示意。
由图 6可知, 燃烧室在第150个数据点时出现故障, 经过GRA-DeepAR模型的预测, 透平排气温度残差绝对值在第106个数据点超过预警线, 在实际故障发生前提前44个数据点发出预警, 并且在此之前没有出现误报情况。
4 结语
采用经典时间序列预测模型进行预测时, 会忽略历史数据中很多潜在的有用信息, 而DeepAR模型是一种基于深度学习的时间序列预测模型, 可以有效解决这一问题。针对燃气轮机燃烧室故障预警现状, 提出了GRA-DeepAR预测模型, 利用概率分布拟合设定预警阈值, 通过监测透平排气温度真实值与预测值之间的残差绝对值曲线, 能够有效判断当前燃烧室工作状态是否正常, 一旦残差绝对值超过预警阈值将立刻发出故障预警信号, 提醒工作人员进行相应的处理。相比于ARIMA和LSTM两种经典时间序列预测模型, GRA-DeepAR预测模型具有更优的预测效果, 同时它能够在一定程度上减轻对数据的要求。需要注意的是, 本文只针对一个型号的燃气轮机进行了故障预警探讨, 在以后的研究中, 会对其他型号的燃气轮机进行分析, 并探索运用概率预测实现故障预警。
参考文献
-
[1]李名家, 钱程, 何万国, 等. 燃气轮机燃烧室故障分析及试验研究[J]. 热能动力工程, 2010, 25(5): 478-481.
-
[2]王文杰, 余又红, 杨东. 某型舰用燃气轮机燃烧室故障原因分析及排除[J]. 燃气轮机技术, 2007, 20(2): 64-67.
-
[3]黄一枫, 茅大钧. 基于数据驱动的发电设备在线预警研究[J]. 电工电气, 2017(7): 15-19. DOI:10.3969/j.issn.1007-3175.2017.07.004
-
[4]叶家豪, 魏霞, 黄德启, 等. 基于灰色关联分析的BSO-ELM-AdaBoost风电功率短期预测[J]. 太阳能学报, 2022, 43(3): 426-432.
-
[5]黄伟, 张泽发. 基于相似度分析的电站燃气轮机燃烧室故障预警研究[J]. 上海电力大学学报, 2020, 36(3): 220-224. DOI:10.3969/j.issn.2096-8299.2020.03.003
-
[6]彭道刚, 姬传晟, 涂煊, 等. 基于LSTM-SVM的燃气轮机压气机故障预警研究[J]. 动力工程学报, 2021, 41(5): 394-399.
-
[7]SALINAS D, FLUNKERT V, GASTHAUS J, et al. DeepAR: probabilistic forecasting with autoregressive recurrent networks[J]. International Journal of Forecasting, 2020, 36(3): 1181-1191. DOI:10.1016/j.ijforecast.2019.07.001
-
[8]朱麟海. 燃气轮机高温部件故障早期预警[D]. 哈尔滨: 哈尔滨工业大学, 2016.
-
[9]ZHANG J C, ZUO X Q, XU M Y, et al. Base station network traffic prediction approach based on LMA-DeepAR[C]//2021 IEEE 6th International Conference on Computer and Communication Systems. Chengdu, China: IEEE, 2021.
-
[10]ZHANG D H, QIAN L Y, MAO B J, et al. A data-driven design for fault detection of wind turbines using random frests and XGBoost[J]. IEEE Access, 2018, 6: 21020-21031.
-
[11]刘思峰, 蔡华, 杨英杰, 等. 灰色关联分析模型研究进展[J]. 系统工程理论与实践, 2013, 33(8): 2041-2046.
-
[12]胡志鹏, 何皑. 基于余弦定理的燃气轮机燃烧故障诊断方法[J]. 燃气轮机技术, 2019, 32(1): 21-25.
-
[13]毛华军. 燃气轮机排气温度监视和保护功能分析[J]. 华电技术, 2009, 31(8): 11-15.
-
[14]魏书荣, 张鑫, 符杨, 等. 基于GRA-LSTM-Stacking模型的海上双馈风力发电机早期故障预警与诊断[J]. 中国电机工程学报, 2021, 41(7): 2373-2383.
-
[15]DONG M, WU H Y, HU H, et al. Deformation prediction of unstable slopes based on real-time monitoring and DeepAR model[J]. Sensors, 2020, 21(1): 14.