|
|
|
发布时间: 2023-02-28 |
清洁安全发电 |
|
|
|
收稿日期: 2022-07-14
基金项目: 国家自然科学基金(62176176, 21606159);山西省重点研发计划项目(201803D121039)
中图法分类号: TM73;TM76
文献标识码: A
文章编号: 2096-8299(2023)01-0025-08
|
摘要
为提高计算效率, 并针对传统拉格朗日松弛算法(LR)在优化过程中存在对偶间隙不能收敛的问题, 提出了一种改进的拉格朗日松弛算法(LR-CMSCA)以优化大规模机组组合问题。首先通过正弦余弦算法(SCA)优化拉格朗日乘子的更新路径, 以缓解振荡现象; 然后在SCA中引入柯西变异算子对当前粒子进行干扰, 尽可能避免陷入局部最优, 并引入自适应权重更新策略, 使粒子更快逼近最优解; 最后利用不同机组规模的电力系统进行仿真计算, 并将计算结果与其他算法进行比较。结果表明, 该方法在计算结果上具有优势, 且有实际应用价值。
关键词
机组组合; 拉格朗日松弛算法; 正弦余弦算法; 柯西变异算子; 自适应权重更新策略
Abstract
In order to improve the computational efficiency, and to solve the problem that the dual gap cannot converge in the traditional Lagrangian relaxation algorithm in the optimization process, an improved Lagrangian relaxation algorithm is proposed to optimize the large-scale unit commitment problem.The method firstly optimizes the update path of Lagrange multipliers through the sine cosine algorithm to alleviate the oscillation, and secondly introduces the Cauchy mutation operator into the sine cosine algorithm to interfere with the current particle, so as to avoid falling into local optimum as much as possible and introduce adaptive weight update strategy to make particles approach the optimal solution faster.Finally, the power system of the units is used for simulation calculation, and the calculation results are compared with other algorithms.The results show that this method has advantages in calculation results and has practical application value.
Key words
unit commitment; Lagrangian relaxation; sine cosine algorithm; Cauchy mutation operator; adaptive weight update strategy
随着生产力水平的快速提高, 人们对电力的需求不断增加, 传统火力发电的成本快速上升, 也带来了环境污染问题[1]。中国在减排方面需要发挥重要作用[2], 在“碳达峰”和“碳中和”的背景下[3-4], 科学决策机组组合问题, 充分利用资源, 既可以减少环境污染问题, 又可以实现经济效益的最大化。
机组组合问题被认为是一个NP-hard问题, 具有非凸性、非线性、高维等特点[5]。目前解决机组组合问题的方法很多, 经典的方法有优先顺序法、动态规划法[6-7]、拉格朗日松弛(Lagrangian Relaxation, LR)算法[8]等。优先顺序法较为简单, 但得到的解的质量通常不是很好; 动态规划法易于保持解的可行性, 但容易陷入维度灾难, 优化求解时间过长; 智能算法包括粒子群(Particle Swarm Optimization, PSO)算法[9-11]、遗传算法(Genetic Algorithm, GA)[12-14]等。PSO算法具有较好的鲁棒性, 但搜索速度较慢, 容易陷入局部最优值, 有学者将PSO算法与其他进化算法相结合来解决优化问题[15-18]。改进遗传算法使GA在机组组合问题上得到了进一步的发展, 但计算效率取决于参数的选择; 禁忌搜索不使用随机数, 不受随机数质量的影响, 但容易陷入局部最优。总体来说, 经典的方法比较简单, 但是从数学的角度看不够严谨, 或者容易造成维数灾难; 智能算法通常需要大量计算, 耗时较长。因此, 许多学者使用混合方法来解决机组组合问题, 但这些算法在具体应用中存在局限性, 场景不同, 算法效果会受到影响。大量文献表明, 拉格朗日松弛算法是解决NP-hard问题的有效算法, 在实际应用中, 会出现对偶间隙不能收敛的现象, 通过不断调整拉格朗日乘数, 可以在合理的时间内得到更好的近似最优解, 但乘子的更新路径会影响算法的有效性, 因此需要采取一些措施来缩小对偶间隙[19]。
本文提出了一种改进的拉格朗日松弛算法LR-CMSCA。首先建立大规模的机组组合模型, 然后采用LR-CMSCA对模型进行优化求解, 最后进行数值仿真和结果分析。
1 机组组合数学模型
1.1 目标函数
本文考虑一个单目标优化问题。我们每时每刻都需要不同的电量, 为保证电力供需平衡, 需要提前规划好开机机组。为了解决停机问题, 需要将启动和停机成本包含在总发电成本Tc中, 即
| $ T_{\mathrm{c}}=\min \sum\limits_{t=1}^T \sum\limits_{i=1}^N\left[O_{\mathrm{c} i}\left(P_i^t\right) u_i^t+R_{\mathrm{c} i}^t\left(1-u_i^{t-1}\right) u_i^t\right] $ | (1) |
式中: T——总时段数;
t——第t个时段, t=1, 2, 3, …, T;
Oci(Pit)——机组i(i=1, 2, 3, …, N)在时间t的发电成本, 即消耗化石能源的燃料成本;
uit——机组i在时间t的状态;
Rcit——机组i的启动成本。
当uit =1时, 表示机组i在时间t运行; 当uit =0时, 表示t时刻机组i处于停机状态。机组i的运行成本可以表示为以下二次函数
| $ O_{\mathrm{c} i}\left(P_i^t\right)=a_i\left(P_i^t\right)^2+b_i P_i^t+c_i $ | (2) |
式中: ai、bi、ci——机组i的煤炭消耗成本系数;
Pit——机组i在时间t的出力大小。
当机组设备关闭后, 将开始冷却。根据机组停机时间的长短, 启动可分为热启动和冷启动, 即
| $ R_{\mathrm{ci}}^t=\left\{\begin{array}{l} H_{\mathrm{s} i}, M_{\mathrm{T} i, \mathrm{~d}} \leqslant T_{i, \mathrm{off}}^t \leqslant M_{\mathrm{T} i, \mathrm{~d}}+C_{\mathrm{T} i} \\ C_{\mathrm{s} i}, T_{i, \mathrm{off}}^t>M_{\mathrm{T} i, \mathrm{~d}}+C_{\mathrm{T} i} \end{array}\right. $ | (3) |
式中: Hsi——机组i的热启动费用, 热启动费用相对较低;
Csi——机组i的冷启动费用, 冷启动费用相对较高;
MTi, d——机组i的最小连续停机时间;
Ti, offt——机组i在t时刻的停机时长;
CTi——机组i的冷启动时间。
1.2 约束条件
为了使模型更贴合实际, 需要考虑以下约束条件。
(1) 系统功率平衡约束。在任何时间段开启的所有机组的输出之和等于所需负载功率。
| $ \sum\limits_{i=1}^N u_i^t P_i^t=P_{\mathrm{D}}^t $ | (4) |
式中: PDt——t时段所需的总功率, 即负载功率。
(2) 最小开停机约束。机组一般不能频繁启停, 需要满足最小启停时间。设Ti, ont代表第i个机组在t时段的连续运行时间, MTi, up表示第i个机组的最小连续运行时间, 如果连续运行时间Ti, ont小于最小连续运行时间MTi, up, 则该机组继续保持开机; 如果连续停机时间Ti, offt小于最小连续停机时间MTi, d, 则该机组不能开机。
| $ T_{i, \mathrm{on}}^t \geqslant M_{\mathrm{Ti}, \mathrm{up}}, T_{i, \mathrm{on}}^{t} \geqslant M_{\mathrm{Ti}, \mathrm{d}} $ | (5) |
(3) 机组出力上下限约束。机组在运行时需要满足自身出力大小约束, 即
| $ P_{i, \min } \leqslant P_i^t \leqslant P_{i, \max } $ | (6) |
式中: Pi、min、Pi, max——第i个机组的最小和最大发电量。
(4) 系统旋转备用约束。电力的突然中断会带来许多不便, 甚至造成严重后果。为了应对一些突发状况, 如机组故障或者负荷大幅波动, 需要引入旋转备用来保障用电的安全和稳定。
| $ \sum\limits_{i=1}^N u_i^t P_{i, \max } \geqslant P_D^t+S_{\mathrm{R} t} $ | (7) |
式中: SRt——系统在t时刻的旋转备用约束量, 在实验中取SRt=0.1PDt。
2 算法介绍
2.1 松弛模型构建
在众多算法中, LR算法因其计算速度快、适用于大规模混合整数规划问题而得到广泛应用。该算法引入了拉格朗日乘子, 形成了不包含耦合约束的原优化问题的对偶问题。这个问题对应的最优值(最小化)只是原问题最优值的一个下界, 因此需要调整拉格朗日乘子多次求解。拉格朗日乘子的选择和修正策略对算法的效率有一定的影响[20-21]。
将系统约束条件加入目标函数中, 引入拉格朗日乘子λt和μt, 可得到拉格朗日函数
| $ \begin{gathered} L_1=T_{\mathrm{c}}+\sum\limits_{t=1}^T \lambda_t\left(P_{\mathrm{D}}^t-\sum\limits_{i=1}^N u_i^t P_i^t\right)+ \\ \sum\limits_{t=1}^T \mu_t\left(P_{\mathrm{D}}^t+S_{\mathrm{R} t}-\sum\limits_{i=1}^N u_i^t P_{i, \max }\right) \end{gathered} $ | (8) |
式中: λt——t时段负荷平衡约束的松弛因子;
μt——t时段备用约束的松弛因子。
将式(1)代入式(8)可得:
| $ \begin{gathered} L_1=\sum\limits_{t=1}^T \sum\limits_{i=1}^N\left[O_{\mathrm{c} i}\left(P_i^t\right) u_i^t+R_{\mathrm{c} i}^t\left(1-u_i^{t-1}\right) u_i^t-\right. \\ \left.\lambda_t u_i^t P_i^t-\mu_t u_i^t P_{i, \max }\right]+ \\ \sum\limits_{t=1}^T\left[\lambda_t P_{\mathrm{D}}^t+\mu_t\left(P_{\mathrm{D}}^t+S_{\mathrm{R} t}\right)\right] \end{gathered} $ | (9) |
采用拉格朗日松弛算法求解, 原函数的最优值J*与对偶问题的最优值q*之间的差异称为“对偶间隙”。本文采用相对对偶间隙Q*来表示, 即
| $ Q^*=\frac{J^*-q^*}{q^*} $ | (10) |
随着求解过程的进行, 对偶间隙逐渐缩小, 并且对偶间隙随着机组数目的增加而减小, 可将对偶间隙的大小作为是否停止迭代的准则。
2.2 正弦余弦算法概述
正弦余弦算法(Sine Cosine Algorithm, SCA)由澳大利亚学者MIRJALILI S在2016年提出[22]。与其他元启发式智能优化算法不同, SCA利用三角函数Sine和Cosine的周期性和波动性特征来实现算法的搜索和优化, 最终得到满足适应度要求的满意解。本文利用SCA的随机搜索性及其较强的全局搜索能力和局部开发能力, 将其与LR算法相结合, 优化拉格朗日乘子的迭代路径, 缩小相对对偶间隙, 提高可行解的精确度。
到目前为止, SCA及其许多改进算法已成功应用于优化领域[23-24]。SCA在标准测试函数中其优化精度和收敛速度均优于PSO和GA等。
设Xi为第i个个体的位置, i=1, 2, 3, …, N, N为种群规模, f(Xi)为第i个个体的目标函数值, Xi*为种群中最优个体的空间位置。在搜索过程中, 第i个个体在下一次迭代过程中空间位置的更新公式为
| $ \begin{aligned} & X_i(t+1)= \\ & \left\{\begin{array}{l} X_i(t)+r_1 \times \sin r_2 \times \\ \left|r_3 \times X_i^*-X_i(t)\right|, \quad r_4<0.5 \\ X_i(t)+r_1 \times \cos r_2 \times \\ \left|r_3 \times X_i^*-X_i(t)\right|, \quad r_4 \geqslant 0.5 \end{array}\right. \end{aligned} $ | (11) |
| $ r_1=a-\theta \frac{a}{\theta_{\max }} $ | (12) |
式中: Xi(t+1)——第i个个体第t+1次迭代解的位置;
Xi(t)——第i个个体第t次迭代解的位置;
r1——线性递减函数, 描述了迭代时的步长, 大小根据式(12)进行调整;
r2——[0, 2π]的随机数, 表示解的更新方向;
r3——[0, 2]的随机权重, 表示当前最优解的影响力;
r4——[0, 1]之间的随机数, 用于选择位置更新方程;
a——常数, 取a=2;
θmax——最大迭代次数。
在SCA中, r3是当前最优解的随机权重。为了能最大程度地保留优势粒子, 淘汰劣势粒子, 本文采用自适应权重更新策略来更新r3。具体表达式为
| $ r_3=\left\{\begin{array}{l} r_{\min }+\left(r_{\max }-r_{\min }\right) \frac{f_i-f_{\min }}{f_{\mathrm{avg}}-f_{\min }}, f \leqslant f_{\mathrm{avg}} \\ r_{\max }, f>f_{\mathrm{avg}} \end{array}\right. $ | (13) |
式中: rmin、rmax ——r3的最小值与最大值;
fi——粒子i的适应度值;
fmin——当前所有粒子的最小适应度值;
favg——当前所有粒子的平均适应度值。
对于适应度值大于平均适应度值的粒子, 应该有较大的权重, 以最大程度保留该粒子; 反之, 取较小的权重。
早有学者证明相比传统的高斯变异算子, 柯西变异具有更强的搜索能力。一维柯西分布的概率密度函数为
| $ d(x)=\frac{1}{\pi} \cdot \frac{t}{t^2+x^2}, \quad-\infty<x<+\infty $ | (14) |
当t=1时为标准柯西分布。柯西分布函数为
| $ D(x)=\frac{1}{\pi} \arctan \left(\frac{x}{t}\right)+\frac{1}{2} $ | (15) |
在原点处柯西分布的峰值小于高斯分布, 两端接近于零的速度也小于高斯分布, 使得个体有更高的概率逃离局部最优, 产生的后代与父本差异较大, 因此本文引入柯西变异来增加种群的多样性, 逃离局部最优解。
对粒子的状态Xi (t) 进行自适应变异, 即
| $ X_i^{\prime}(t)=X_i(t)+X_i(t) C(0, 1) $ | (16) |
式中: C(0, 1)——柯西分布产生的随机值。
当粒子与当前最优粒子的位置距离越近, 表明种群间的相似性越大, 将距离当前最优粒子最远的个体进行柯西变异, 如果变异后粒子的适应度值大于原适应度值, 则变异后的粒子代替原粒子, 否则保持不变。
2.3 LR-CMSCA算法介绍
机组组合问题约束条件较多, 本身具有一定的难度, 当机组规模较大时, 则问题更具有挑战性。本文提出的LR-CMSCA算法总体步骤如下:
(1) 导入所有电力系统数据, 如最大和最小发电功率、启动成本、最小启停时间、成本系数等;
(2) 初始化参数及拉格朗日乘子;
(3) 判断是否达到最大迭代次数, 如果是, 则转到步骤(10), 否则进入步骤(4);
(4) 建立T个时段的启停问题及原问题的对偶问题;
(5) 求解对偶函数的最优解及各机组的出力大小;
(6) 判断是否为可行解, 如果不是, 转到步骤(7), 如果是, 转到步骤(8);
(7) 用SCA对拉格朗日乘子λt和μt进行调整, 并对距离当前最优解较远的解进行柯西变异, 将变异后的解与原解进行比较, 保留较好的解, 迭代次数加1, 返回步骤(3);
(8) 计算原问题的目标函数值;
(9) 判断对偶间隙是否满足要求, 如果满足, 转到步骤(10), 否则转到步骤(7);
(10) 算法结束。
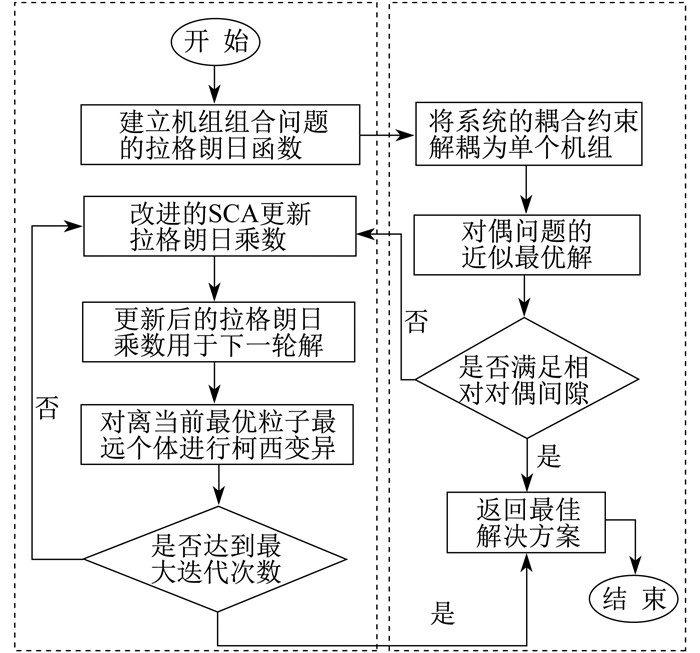
图 1为LR-CMSCA算法流程示意。
3 数值仿真结果与分析
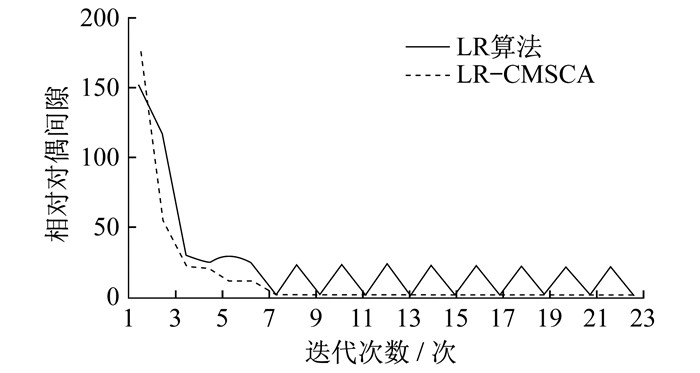
为了验证本文所提算法的有效性, 将LR算法与LR-CMSCA在10机组系统中的相对对偶间隙变化进行比较, 如图 2所示。由图 2可知, 在LR算法的求解过程中, 相对对偶间隙先快速减小, 然后振荡, 不能收敛, 最终的解决方案未必可行; LR-CMSCA可以很好地改善振荡现象, 最终稳定收敛, 这主要得益于SCA的搜索随机性。
表 1为不同机组系统中相对对偶间隙变化比较。由表 1可知, 相同迭代次数时, 机组规模越大, 相对对偶间隙越小, 如10机组系统第8次迭代时相对对偶间隙是0.023, 而80机组系统第8次迭代时相对对偶间隙下降到了0.010, 表明机组规模越大精度越高, 收敛速度越快。
表 1
不同机组系统中相对对偶间隙的变化
| 机组系统 | 迭代次数/次 | 相对对偶间隙 |
| 10 | 8 | 0.023 |
| 20 | 5 | 0.017 |
| 40 | 4 | 0.015 |
| 60 | 4 | 0.012 |
| 80 | 8 | 0.010 |
| 100 | 7 | 0.010 |
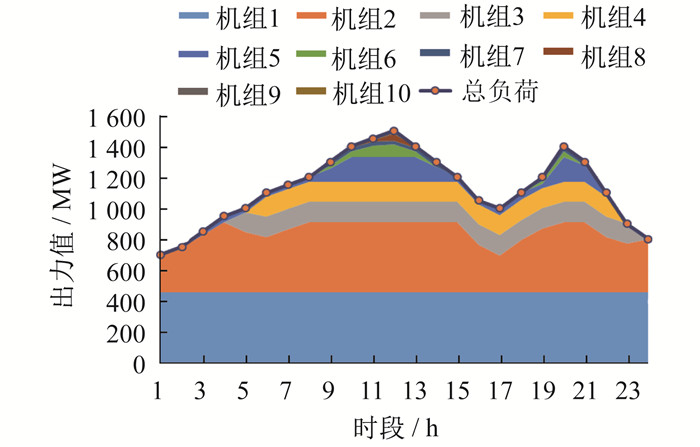
为了进一步验证LR-CMSCA的有效性, 本文分别对不同规模的火电机组进行仿真, 仿真在MATLAB 2020a环境下进行, 并与其他文献所提算法进行比较。在本案例中, 首先在一个典型的10机组系统中进行仿真, 10机组系统的总负荷需求如表 2所示, 特性参数如表 3所示, LR-CMSCA最终得到的10机组调度结果如表 4所示。表 4中, “1”表示投运, “0”表示关闭。10机组出力总值等于负荷总需求, 各机组出力结果如表 5所示, 出力平衡约束如图 3所示。调度时, 在满足负荷需求的情况下, 尽可能优先考虑成本较低的机组。因此, 由表 4可知, 1#和2#机组都是24 h投入的; 由表 5可知, 总成本为564 000 $。
表 2
总负荷需求
| 时段 | 负荷 | 时段 | 负荷 | |
| 1 | 700 | 13 | 1 400 | |
| 2 | 750 | 14 | 1 300 | |
| 3 | 850 | 15 | 1 200 | |
| 4 | 950 | 16 | 1 050 | |
| 5 | 1 000 | 17 | 1 000 | |
| 6 | 1 100 | 18 | 1 100 | |
| 7 | 1 150 | 19 | 1 200 | |
| 8 | 1 200 | 20 | 1 400 | |
| 9 | 1 300 | 21 | 1 300 | |
| 10 | 1 400 | 22 | 1 100 | |
| 11 | 1 450 | 23 | 900 | |
| 12 | 1 500 | 24 | 800 |
表 3
10机组系统的特性参数
| 参数 | 机组 | |||||||||
| 1# | 2# | 3# | 4# | 5# | 6# | 7# | 8# | 9# | 10# | |
| Pi, max/MW | 455 | 455 | 130 | 130 | 162 | 80 | 85 | 55 | 55 | 55 |
| Pi, min/MW | 150 | 150 | 20 | 20 | 25 | 20 | 25 | 10 | 10 | 10 |
| ai/[$·(MW2h)-1] | 0.000 48 | 0.000 31 | 0.002 | 0.002 11 | 0.003 98 | 0.007 12 | 0.000 79 | 0.004 13 | 0.002 22 | 0.001 73 |
| bi/[$·(MWh)-1] | 16.19 | 17.26 | 16.60 | 16.50 | 19.70 | 22.26 | 27.74 | 25.92 | 27.27 | 27.79 |
| ci/($·h-1) | 1 000 | 970 | 700 | 680 | 450 | 370 | 480 | 660 | 665 | 670 |
| Hsi/$ | 4 500 | 5 000 | 550 | 560 | 900 | 170 | 260 | 30 | 30 | 30 |
| Csi/$ | 9 000 | 10 000 | 1 100 | 1 120 | 1 800 | 340 | 520 | 60 | 60 | 60 |
| MTi, d/h | 8 | 8 | 5 | 5 | 6 | 3 | 3 | 1 | 1 | 1 |
| MTi, up/h | 8 | 8 | 5 | 5 | 6 | 3 | 3 | 1 | 1 | 1 |
| CTi/h | 5 | 5 | 4 | 4 | 4 | 2 | 2 | 0 | 0 | 0 |
| 机组初始状态/h | 8 | 8 | -5 | -5 | -6 | -3 | -3 | -1 | -1 | -1 |
表 4
10机组最优调度结果
| 时段 | 机组 | |||||||||
| 1# | 2# | 3# | 4# | 5# | 6# | 7# | 8# | 9# | 10# | |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 4 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 5 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 6 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 7 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 8 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 9 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 10 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 11 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 12 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 13 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 14 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 |
| 15 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 16 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 17 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 18 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 19 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 20 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 |
| 21 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 |
| 22 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 23 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 24 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
表 5
10机组经济调度
| 时段 | 机组出力/MW | 负荷/MW | |||||||||
| 1# | 2# | 3# | 4# | 5# | 6# | 7# | 8# | 9# | 10# | ||
| 1 | 455 | 245 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 700 |
| 2 | 455 | 295 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 750 |
| 3 | 455 | 370 | 0 | 0 | 25 | 0 | 0 | 0 | 0 | 0 | 850 |
| 4 | 455 | 455 | 0 | 0 | 40 | 0 | 0 | 0 | 0 | 0 | 950 |
| 5 | 455 | 390 | 130 | 0 | 25 | 0 | 0 | 0 | 0 | 0 | 1 000 |
| 6 | 455 | 360 | 130 | 130 | 25 | 0 | 0 | 0 | 0 | 0 | 1 100 |
| 7 | 455 | 410 | 130 | 130 | 25 | 0 | 0 | 0 | 0 | 0 | 1 150 |
| 8 | 455 | 455 | 130 | 130 | 30 | 0 | 0 | 0 | 0 | 0 | 1 200 |
| 9 | 455 | 455 | 130 | 130 | 85 | 20 | 25 | 0 | 0 | 0 | 1 300 |
| 10 | 455 | 455 | 130 | 130 | 162 | 33 | 25 | 10 | 0 | 0 | 1 400 |
| 11 | 455 | 455 | 130 | 130 | 162 | 73 | 25 | 10 | 10 | 0 | 1 450 |
| 12 | 455 | 455 | 130 | 130 | 162 | 80 | 25 | 43 | 10 | 10 | 1 500 |
| 13 | 455 | 455 | 130 | 130 | 162 | 33 | 25 | 10 | 0 | 0 | 1 400 |
| 14 | 455 | 455 | 130 | 130 | 95 | 0 | 25 | 10 | 0 | 0 | 1 300 |
| 15 | 455 | 455 | 130 | 130 | 30 | 0 | 0 | 0 | 0 | 0 | 1 200 |
| 16 | 455 | 310 | 130 | 130 | 25 | 0 | 0 | 0 | 0 | 0 | 1 050 |
| 17 | 455 | 240 | 130 | 130 | 45 | 0 | 0 | 0 | 0 | 0 | 1 000 |
| 18 | 455 | 340 | 130 | 130 | 45 | 0 | 0 | 0 | 0 | 0 | 1 100 |
| 19 | 455 | 415 | 130 | 130 | 25 | 20 | 25 | 0 | 0 | 0 | 1 200 |
| 20 | 455 | 455 | 130 | 130 | 162 | 33 | 25 | 0 | 10 | 0 | 1 400 |
| 21 | 455 | 455 | 130 | 130 | 105 | 0 | 25 | 0 | 0 | 0 | 1 300 |
| 22 | 455 | 360 | 130 | 130 | 25 | 0 | 0 | 0 | 0 | 0 | 1 100 |
| 23 | 455 | 315 | 130 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 900 |
| 24 | 455 | 345 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 800 |
为了避免偶然性, 本文将LR-CMSCA与文献[8]的LR算法、文献[13]的GA算法、文献[25]的ELRPSO算法、文献[22]的SCA算法在10、20、40、60、80、100机组系统中进行了仿真分析比较, 每种算法分别运行20次, 记录最优值, 仿真结果如表 6所示。由表 6可知, 与其他4种算法相比, 本文算法提供了较好的解决方案, 且机组规模越大效果越明显。这表明SCA是更新拉格朗日乘子的一种有效方法。通过引入柯西变异算子和自适应权重更新策略, 可以增加种群的多样性, 使粒子更快地向最优解移动。
表 6
不同机组系统中各算法的仿真结果比较
| 机组 系统 |
仿真结果/($·d-1) | ||||
| LR[8] | GA[13] | SCA[22] | ELRPSO[25] | LR-CMSCA | |
| 10 | 566 104 | 565 868 | 564 300 | 564 002 | 564 000 |
| 20 | 1 130 500 | 1 128 923 | 1 126 875 | 1 128 615 | 1 120 100 |
| 40 | 2 262 023 | 2 261 907 | 2 256 523 | 2 258 903 | 2 248 633 |
| 60 | 3 400 005 | 3 387 672 | 3 386 100 | 3 386 875 | 3 369 955 |
| 80 | 4 531 029 | 4 526 500 | 4 526 024 | 4 525 893 | 4 481 033 |
| 100 | 5 664 593 | 5 656 842 | 5 650 689 | 5 660 051 | 5 590 057 |
4 结语
针对LR算法在解决大规模机组组合时对偶间隙无法收敛的现象, 利用SCA随机搜索能力强的优点, 提出了一种新的改进算法LR-CMSCA, 并在不同规模机组系统中采用仿真实验测试该算法。实验结果表明, LR-CMSCA具有优越性, 传统LR算法对偶间隙不能收敛的现象得到抑制, 运行效率高, 且机组规模越大, 效果越好, 具有较好的应用前景。
参考文献
-
[1]孙智滨, 康英伟, 常俊, 等. 大型燃煤火电机组湿法脱硫系统控制研究[J]. 上海电力大学学报, 2020, 36(6): 553-561. DOI:10.3969/j.issn.2096-8299.2020.06.007
-
[2]LIU Z, DENG Z, HE G, et al. Challenges and opportunities for carbon neutrality in China[J]. Nature Reviews Earth & Environment, 2021, 3(2): 141-155.
-
[3]MALLAPATY S. How China could be carbon neutral by mid-century[J]. Nature, 2020, 586: 482-483. DOI:10.1038/d41586-020-02927-9
-
[4]殷闯. 燃煤火电与水泥行业污染物排放标准的对比分析与控制[J]. 上海电力大学学报, 2021, 37(2): 176-178. DOI:10.3969/j.issn.2096-8299.2021.02.014
-
[5]ABDI H. Profit-based unit commitment problem: a review of models, methods, challenges, and future directions[J]. Renewable and Sustainable Energy Reviews, 2021, 138: 110504. DOI:10.1016/j.rser.2020.110504
-
[6]XU Y, DING T, QU M, et al. Adaptive dynamic programming for gas-power network constrained unit commitment to accommodate renewable energy with combined-cycle units[J]. IEEE Transactions on Sustainable Energy, 2020, 11(3): 2028-2039. DOI:10.1109/TSTE.2019.2951616
-
[7]PUTZ D, SCHWABENEDER D, AUER H, et al. A comparison between mixed-integer linear programming and dynamic programming with state prediction as novelty for solving unit commitment[J]. International Journal of Electrical Power & Energy Systems, 2021, 125: 106426.
-
[8]SCUZZIATO M R, FINARDI E C, ANTONIO F. Solving stochastic hydrothermal unit commitment with a new primal recovery technique based on Lagrangian solutions[J]. International Journal of Electrical Power & Energy Systems, 2021, 127: 106661.
-
[9]戴永彬, 陈海涛. 一种混合引导的偏好多目标粒子群优化算法[J]. 控制工程, 2019, 26(3): 549-554.
-
[10]GE Q B, GUO C, JIANG H Y, et al. Industrial power load forecasting method based on reinforcement learning and PSO-LSSVM.[J]. IEEE Transactions on Cybernetics, 2020, 52(2): 1112-1124.
-
[11]周任军, 李绍金, 陈瑞先, 等. 采用模糊自修正粒子群算法的碳排放权交易冷热电多目标调度[J]. 中国电机工程学报, 2014, 6119-6126.
-
[12]MILLO F, ARYA P, MALLAMO F. Optimization of automotive diesel engine calibration using genetic algorithm techniques[J]. Energy, 2018, 158: 807-819. DOI:10.1016/j.energy.2018.06.044
-
[13]POSTOLOV B, LLIEV A. New metaheuristic methodology for solving security constrained hydrothermal unit commitment based on adaptive genetic algorithm[J]. International Journal of Electrical Power & Energy Systems, 2022, 134: 107163.
-
[14]PANDAY A, BANSAL H O. Energy management strategy for hybrid electric vehicles using genetic algorithm[J]. Journal of Renewable & Sustainable Energy, 2016, 8(1): 741-746.
-
[15]于艾清, 刘滔. 基于自适应量子遗传算法的电力系统机组组合问题[J]. 上海电力学院学报, 2015, 31(1): 24-28.
-
[16]GOUDARZI A, LI Y J, XIANG J. A hybrid non-linear time-varying double-weighted particle swarm optimization for solving non-convex combined environmental economic dispatch problem[J]. Applied Soft Computing, 2020, 86: 105894. DOI:10.1016/j.asoc.2019.105894
-
[17]JOTDEHI A R. A mixed binary-continuous particle swarm optimisation algorithm for unit commitment in microgrids considering uncertainties and emissions[J]. International Transactions on Electrical Energy Systems, 2020, 30(11): 12581.
-
[18]ZHANG J, TANG Q, CHEN Y, et al. A hybrid particle swarm optimization with small population size to solve the optimal short-term hydro-thermal unit commitment problem[J]. Energy, 2016, 109: 765-780.
-
[19]SARAVANAN B, MISHRA S, NAG D. A solution to stochastic unit commitment problem for a wind-thermal system coordination[J]. Frontiers in Energy, 2014(8): 192-200.
-
[20]GUAN X, LUH P B, YAN H, et al. Short-term scheduling of thermal power systems[C]// Power Industry Computer Application Conference. Baltimore, MD, USA. IEEE: 1991.
-
[21]LI X, ZHAI Q Z, ZHOU J X, et al. A variable reduction method for large-scale unit commitment[J]. IEEE Transactions on Power Systems, 2020, 35(1): 261-272.
-
[22]MIRJALILI S. SCA: a sine cosine algorithm for solving optimization problems[J]. Knowledge-Based Systems, 2016, 96: 120-133.
-
[23]LI S, FANG H J, LIU X Y, et al. Parameter optimization of support vector regression basedon sine cosine algorithm[J]. Expert Systems with Application, 2018, 91: 63-77.
-
[24]DAS S, BHATTACHARYA A, CHAKRABORTY A K. Solution of short-term hydrothermal scheduling using sine cosine algorithm[J]. Soft Computing, 2018, 22(19): 6409-6427.
-
[25]YU X, ZHANG X Q. Unit commitment using Lagrangian relaxation and particle swarm optimization[J]. International Journal of Electrical Power & Energy Systems, 2014, 61: 510-522.