|
|
|
发布时间: 2023-02-28 |
清洁安全发电 |
|
|
|
收稿日期: 2022-09-27
中图法分类号: TM621
文献标识码: A
文章编号: 2096-8299(2023)01-0033-07
|
摘要
针对火电厂燃料控制这一非线性、滞后性、强干扰的被控对象, 设计基于改进灰狼优化算法的自抗扰控制器。对燃料控制系统不同工况进行了阶跃仿真实验、扰动测试、鲁棒性测试以及变工况实验。实验结果表明, 相较于传统比例-积分(PI)控制器和专家经验整定的自抗扰控制器, 改进灰狼优化算法的自抗扰控制器可以实现燃料量的快速、稳定调节, 在抗扰动及变工况过程中有较好的控制效果, 具有较强的鲁棒性。
关键词
自抗扰控制器; 火电燃料控制系统; 改进灰狼优化算法
Abstract
Aiming at the controlled object of thermal power plant fuel control, which is nonlinear, large lag and strong disturbance, an active disturbance rejection controller based on the improved grey wolf optimization algorithm is designed.Through the step simulation experiment, disturbance experiment, robustness experiment and variable working condition experiment of the fuel control system is conducted under different working conditions.The experimental results show that, compared with the traditional PI controller and the active disturbance rejection controller based on expert experience, the active disturbance rejection controller based on the improved grey wolf optimization algorithm can realize the fast and stable adjustment of the fuel.It has better control effect in the process of disturbance and variable working condition, and has strong robustness.
Key words
active disturbance rejection controller; thermal power fuel controller system; improved grey wolf optimization algorithm
锅炉是火电机组提供热能动力的主要来源, 锅炉经济和稳定运行对于保障电力生产起着重要作用。锅炉燃料控制系统是一个复杂的控制系统, 具有非线性、滞后性、工作环境扰动因素较多、动态参数随负荷改变等特点。目前燃料控制的核心问题在于快速适应不同自动发电控制负荷指令的变化, 且及时消除内外扰动对系统的影响。
现阶段火电机组燃料控制多采用传统的比例-积分(PI)控制器, 但若系统对象的参数发生变化或者非线性效应显著时, 控制性能降低。近年来, 新型智能控制已经广泛运用于生产实践。预测控制可以根据被控对象的历史记录以及下一时刻的系统输入从而预测系统输出, 但预测控制对计算机的计算能力和计算量要求过高, 不能应用于动态响应速度不高的场合[1]。模糊控制是一种将专家经验和知识总结成模糊规则, 将系统输入信号通过模糊规则完成推理作用到被控对象上的控制方式, 但模糊控制在工况变化时控制效果不佳[2]。针对其他控制器的缺点, 韩京清[3]提出自抗扰控制器, 通过对系统的输入和输出信号提取出干扰信号, 提前用控制信号消除干扰信号对系统的影响。李杰等人[4]指出人工智能算法在参数整定与优化过程中占主导地位。此外, 研究者提出了粒子群优化算法[5]、遗传算法[6]、BP(Back Propagation)神经网络[7]、果蝇算法[8]、改进蜂群算法[9]等。同其他智能算法相比, 灰狼优化算法[10]具有结构简单、调节参数少、收敛速度快、全局优化能力强等特点。
本文设计了针对火电厂燃煤锅炉燃料控制系统的自抗扰控制器。它对灰狼优化算法进行了改进, 并对控制器的关键参数进行寻优, 使得适应度最佳; 同时, 在不同工况下进行了阶跃响应仿真实验、扰动控制仿真分析实验、鲁棒性实验和变负荷仿真实验。结果表明, 相较于其他传统控制器, 基于改进灰狼优化算法的自抗扰控制器可以实现火电燃料的快速稳定调节, 更有效克服扰动对系统的影响, 具有更强的鲁棒性, 在变工况过程中也有更好的调节效果。
1 火电燃料控制系统自抗扰控制器设计
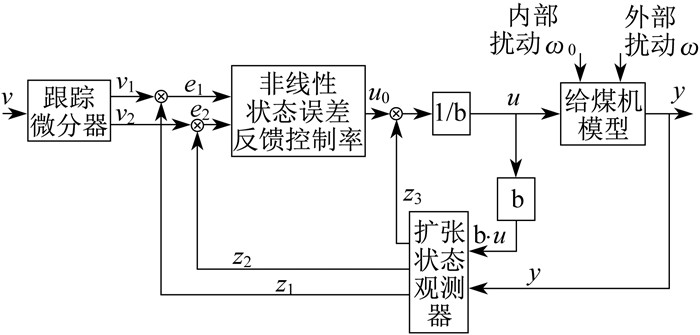
火电燃料控制系统自抗扰控制器(Active Disturbance Rejection Control, ADRC)由跟踪微分器(Tracking Differentiator, TD)、非线性状态误差反馈控制率(Nonlinear State Error Feedback, NSEF)、扩张状态观测器(Extended State Observer, EXO)部分组成[11], 结构如图 1所示。图 1中, v为给煤量给定值, y为实际给煤量, v1为v的跟踪信号, v2为v的微分信号, z1、z2、z3为扩张状态观测器的输出信号, e1、e2为差值信号, b为常数, u为自抗扰控制器计算的给煤机转速, u0为非线性状态误差反馈控制率计算控制量, ω0为给煤机模型内部扰动, ω为给煤机模型外部扰动。给煤量设定值跟随机组自动发电控制指令。
给煤机转速和给煤量之间的动态特性数学模型为
| $ G(s)=\frac{k}{T_{\mathrm{i}} s+1} \mathrm{e}^{-\tau s} $ | (1) |
式中: G(s)——传递函数;
k——比例系数;
Ti——积分时间常数;
τ——延迟时间;
s——拉普拉斯算子。
将延时环节
| $ \mathrm{e}^{\tau s}=1+\tau s+\frac{\tau^2 s^2}{2 !}+\frac{\tau^3 s^3}{3 !}+\frac{\tau^4 s^4}{4 !}+\cdots $ | (2) |
取eτs=1+τs, 将时滞环节e-τs根据等效成惯性环节
| $ G(s)=\frac{k}{\left(T_{\mathrm{i}} s+1\right)(\tau s+1)}=\frac{\frac{k}{T_{\mathrm{i}} \tau}}{s^2+\frac{T_{\mathrm{i}}+\tau}{T_{\mathrm{i}} \tau} s+\frac{1}{T_{\mathrm{i}} \tau}} $ | (3) |
将式(3)等效成微分方程为
| $ \ddot{y}+\frac{T_{\mathrm{i}}+\tau}{T_{\mathrm{i}} \tau} \dot{y}+\frac{1}{T_{\mathrm{i}} \tau} y=\frac{k}{T_{\mathrm{i}} \tau} u $ | (4) |
选取采样时间为1 s, 可将微分方程离散化, 并用差分方程形式表示为
| $ \begin{aligned} & y(k+2)+\frac{T_{\mathrm{i}}+\tau-2 T_{\mathrm{i}} \tau}{T_{\mathrm{i}} \tau} y(k+1)+ \\ & \frac{T_{\mathrm{i}} \tau-T_{\mathrm{i}}-\tau+1}{T_{\mathrm{i}} \tau} y(k)=\frac{k}{T_{\mathrm{i}} \tau} u(k) \end{aligned} $ | (5) |
选择状态变量x1(k)=y(k), x2(k)=y(k+1), 可将式(5)等效成状态空间方程, 即
| $ \left\{\begin{array}{l} {\left[\begin{array}{l} x_1(k+1) \\ x_2(k+1) \end{array}\right]=\boldsymbol{A}\left[\begin{array}{l} x_1(k) \\ x_2(k) \end{array}\right]+B u(k)} \\ y(k)=\boldsymbol{C}\left[\begin{array}{l} x_1(k) \\ x_2(k) \end{array}\right] \end{array}\right. $ | (6) |
其中,
| $ \begin{gathered} \boldsymbol{A}=\left[\begin{array}{c} 0 \\ -\frac{T \tau-T-\tau+1}{T \tau}-\frac{T+\tau-2 T \tau}{T \tau} \end{array}\right], \\ \boldsymbol{B}=\left[\begin{array}{l} 0 \\ \frac{k}{T \tau} \end{array}\right], \\ \boldsymbol{C}=\left[\begin{array}{ll} 1 & 0 \end{array}\right] \end{gathered} $ | (7) |
跟踪微分器的算法表达式为
| $ \left\{\begin{aligned} & e_0(k)=v_1(k)-v(k) \\ & v_1(k+1)= v_1(k)+T v_2(k) \\ & v_2(k+1)= v_2(k)+ \\ & T f_{\mathrm{st}}\left(e_0(k), v_2(k), r, h_0\right) \end{aligned}\right. $ | (8) |
式中: e0(k)——第k个采样时刻v1和v的差值信号;
v1(k)——第k个采样时刻输入信号v的跟踪信号;
v2(k)——第k个采样时刻输入信号v的微分信号;
T——采样时间;
fst(e0(k), v2(k), r, h0)——非线性函数;
r——速度因子;
h0——滤波因子。
| $ f_{\mathrm{st}}\left(e_0, v_2, r, h_0\right)= \begin{cases}-r \cdot \operatorname{sign}(a), & |a|>d \\ -r \cdot \frac{a}{d}, & |a| \leqslant d\end{cases} $ | (9) |
式中: a——非线性函数;
d——速度因子和滤波因子的乘积。
其中,
| $ a= \begin{cases}v_2+\frac{\operatorname{sign}(y) \cdot\left(a_0-d\right)}{2}, & |y|>d_0 \\ v_2+\frac{y}{h_0}, & |y| \leqslant d_0\end{cases} $ | (10) |
| $ a= \begin{cases}v_2+\frac{\operatorname{sign}(y) \cdot\left(a_0-d\right)}{2}, & |y|>d_0 \\ v_2+\frac{y}{h_0}, & |y| \leqslant d_0\end{cases} $ | (11) |
| $ \left\{\begin{array}{l} a_0=\sqrt{d^2+8 \cdot r \cdot|y|} \\ y=e_0+h_0 \cdot v_2 \\ d_0=d \cdot h_0 \end{array}\right. $ | (12) |
式中: a0、y、d0——函数表达式。
非线性状态误差反馈控制率的算法表达式为
| $ \left\{\begin{aligned} e_1(k)= & v_1(k)-z_1(k) \\ e_2(k)= & v_2(k)-z_2(k) \\ u_0(k)= & k_1 \operatorname{fal}\left(e_1(k), a_3, c_3\right)+ \\ & k_2 \mathrm{fal}\left(e_2(k), a_4, c_4\right) \\ u(k)= & \frac{u_0(k)-z_3(k)}{b} \end{aligned}\right. $ | (13) |
式中: e1(k)、e2(k)——第k个采样时刻差值信号;
z1(k)、z2(k)、z3(k)——第k个采样时刻ESO的输出信号;
u0(k)——第k个采样时刻非线性状态误差反馈的输出信号;
k1、k2——比例系数;
u(k)——第k个采样时刻给煤机转速信号;
fal(·)——非线性函数;
a3、a4、c3、c4、b——系统常数。
扩张状态观测器的算法表达式为
| $ \left\{\begin{aligned} &x(k)=z_1(k)-y(k) \\ &z_1(k+1)= z_1(k)+T\left(z_2(k)-\right. \\ &\beta_1\left(z_1(k)-y(k)\right) \\ &z_2(k+1)= z_2(k)+T\left(z_3(k)+\right. \\ &b \cdot u(k)- \\ &\left.\beta_2 \mathrm{fal}\left(x(k), a_1, c_1\right)\right) \\ &z_3(k+1)= z_3(k)-T \beta_3 \mathrm{fal}\left(x(k), a_2, c_2\right) \end{aligned}\right. $ | (14) |
式中: x(k)——第k个采样时刻差值信号;
β1、β2、β3、a1、a2、c1、c2——系统常数;
y(k)——第k个采样时刻实际给煤量信号。
非线性函数fal(x, a, c)表达式为
| $ \operatorname{fal}(x, a, c)=\left\{\begin{array}{l} \frac{x}{c^{1-a}}, |x| \leqslant c \\ |x|^a \cdot \operatorname{sign}(x), |x|>c \end{array}\right. $ | (15) |
自抗扰控制器需要选取的参数包括跟踪微分器的{T, r, h0}, 非线性状态误差反馈控制率的{a3, a4, c3, c4, k1, k2}和扩张状态观测器的{a1, a2, b, c1, c2, β1, β2, β3}。选取火电燃料控制系统ADRC的初始参数[12]: T=1, h0=0.5, r=200, a1=0.5, a2=0.25, a3=0.75, a4=1.05, c1=c2=0.000 1, c3=c4=0.3。而{β1, β2, β3, k1, k2, b}则可以通过人工智能算法进行参数整定。
2 改进灰狼优化算法对控制器参数整定
灰狼优化算法[13]主要是通过模拟灰狼种群的群体狩猎行为衍生出的一种新型智能优化算法。在迭代寻优过程中, 可根据适应度划分灰狼等级。将适应度最佳的前3头狼从优到劣分别命名为α狼、β狼、δ狼。灰狼在向猎物移动的过程中, 位置更新方式为
| $ \left\{\begin{array}{l} \boldsymbol{D}=\left|\boldsymbol{F} \boldsymbol{X}_{\mathrm{p}}(k)-\boldsymbol{X}(k)\right| \\ \boldsymbol{X}(k+1)=\boldsymbol{X}_{\mathrm{p}}(k)-\boldsymbol{E} \boldsymbol{D} \end{array}\right. $ | (16) |
式中: D——灰狼个体与猎物之间的距离向量;
k——迭代次数;
Xp(k)——第k次迭代灰狼的位置向量;
X(k)——第k次迭代猎物的位置向量;
F、E——系数向量。
其中,
| $ \left\{\begin{array}{l} \boldsymbol{E}=2 a \cdot \boldsymbol{r}_1-a \\ \boldsymbol{F}=2 \cdot \boldsymbol{r}_2 \end{array}\right. $ | (17) |
式中: r1、r2——[0, 1]的随机数;
a——收敛因子。
本文将收敛因子改进成如下形式为
| $ a=2-2\left[\frac{1}{\mathrm{e}-1} \times\left(\mathrm{e}^{\frac{k}{k_{\max }}}-1\right)\right] $ | (18) |
式中: k——当前迭代次数;
kmax——最大迭代次数。
在灰狼群体狩猎猎物过程中, 因为头狼α, β, δ的位置最接近猎物, 因此计算出头狼α, β, δ位置的平均值并指导狼群逼近此位置即可达到狩猎的目的, 其数学公式为
| $ \left\{\begin{array}{l} D_\alpha=\left|\boldsymbol{C}_1 \boldsymbol{X}_\alpha(k)-\boldsymbol{X}(k)\right| \\ D_\beta=\left|\boldsymbol{C}_2 \boldsymbol{X}_\beta(k)-\boldsymbol{X}(k)\right| \\ D_\delta=\left|\boldsymbol{C}_3 \boldsymbol{X}_\delta(k)-\boldsymbol{X}(k)\right| \end{array}\right. $ | (19) |
式中: Dα、Dβ、Dδ——头狼α、β、δ与灰狼个体之间的位置;
Xα、Xβ、Xδ——头狼α、β、δ的位置;
C1、C2、C3——系数向量;
X(k)——灰狼个体的位置向量。
灰狼个体朝向α狼、β狼、δ狼前进的方向向量为
| $ \left\{\begin{array}{l} \boldsymbol{X}_1=\boldsymbol{X}_\alpha-\boldsymbol{A}_1 \cdot D_\alpha \\ \boldsymbol{X}_2=\boldsymbol{X}_\beta-\boldsymbol{A}_2 \cdot D_\beta \\ \boldsymbol{X}_3=\boldsymbol{X}_\delta-\boldsymbol{A}_3 \cdot D_\delta \end{array}\right. $ | (20) |
式中: X1、X2、X3——灰狼个体向头狼α、β、δ前进的方向向量;
A1、A2、A3——系数向量。
灰狼种群的最终方向向量为
| $ \boldsymbol{X}(k+1)=\frac{\boldsymbol{X}_1+\boldsymbol{X}_2+\boldsymbol{X}_3}{3} $ | (21) |
本文选取时间与系统给煤量设定值与实际给煤量偏差绝对值乘积的积分值[14]作为适应度函数。
| $ \text { fitness }=\sum\limits_{k=1}^m k \cdot|y(k)-v(k)| \cdot T $ | (22) |
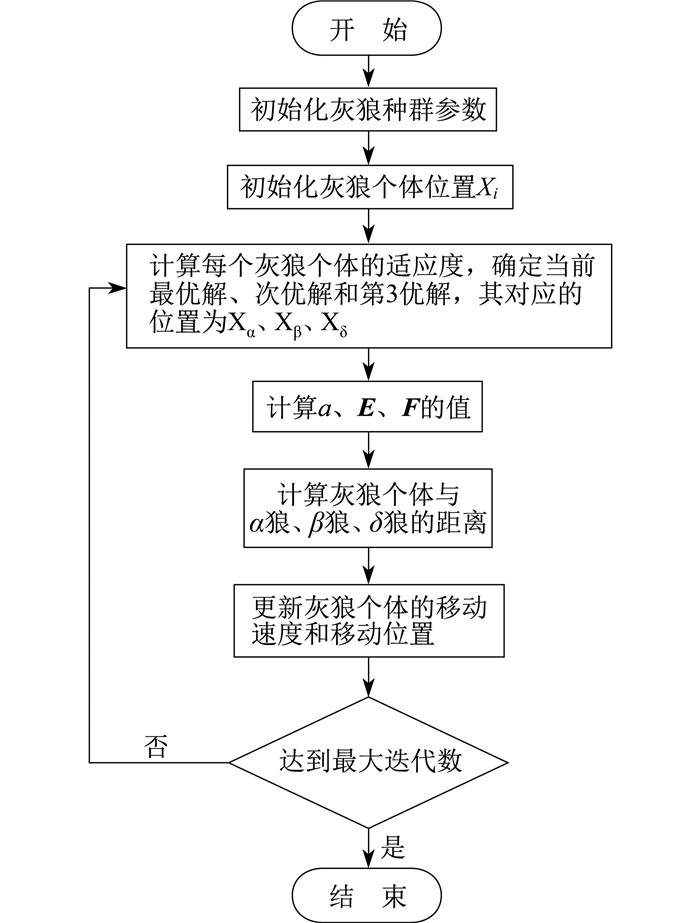
算法流程如图 2所示。
3 火电燃料控制系统仿真分析
3.1 火电燃料控制系统模型建立
火电厂燃料控制系统中给煤机给料皮带较长, 当给煤量设定值发生变化时, 给煤机出料口的给煤量容易出现较大的延迟。当每台锅炉的负荷发生变化时, 给煤机转速和给煤量的动态特性发生明显变化。给煤机自身可能出现堵煤、断煤等现象, 具有扰动变量多等特点。
以某600 MW机组燃料控制系统在90%负荷和50%负荷下建立给煤机转速和给煤量之间的动态特性。状态空间模型如表 1所示。
表 1
不同工况下给煤机转速-给煤量的状态空间模型参数
| 工况 | 系数矩阵A | 系数矩阵BT | 系数矩阵C |
| 90% 负荷 |
|||
| 50% 负荷 |
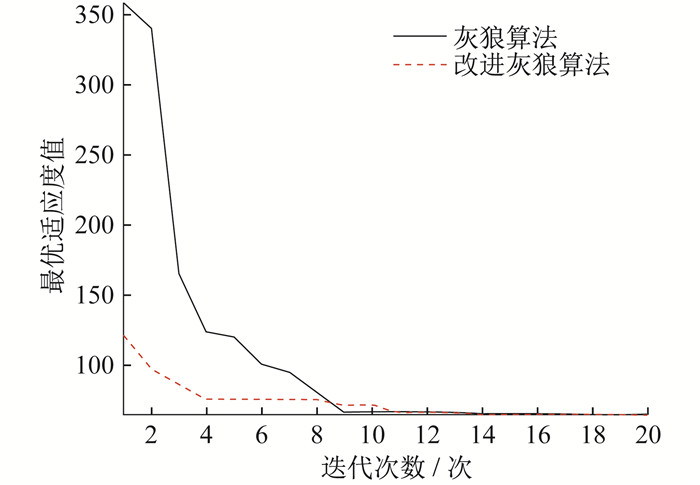
3.2 改进灰狼算法与传统灰狼算法比较
传统灰狼优化算法收敛因子a=2(1-k/kmax)。本文将收敛因子改进成
结果表明, 灰狼算法在第14次迭代时适应度达到最优值, 改进灰狼算法在第19次迭代时适应度达到最优值, 改进灰狼算法的适应度更优。
3.3 火电燃料控制仿真结果分析
在90%负荷和50%负荷下, 分别采用改进灰狼算法优化的自抗扰控制器、经验整定的比例-积分控制器和自抗扰控制器进行参数优化。两种工况下参数优化结果如表 2所示。
表 2
两种工况下参数优化结果
| 工况 | 控制器 | 优化参数 |
| 90% 负荷 |
基于改进灰狼算法优化自抗扰控制器 | β1=8.66, β2=270.68, β3=18.54, k1=75.61, k2=205.8, b0=0.1 |
| 基于经验优化自抗扰控制器 | β1=15, β2=20, β3=5, k1=10, k2=152, b0=0.42 | |
| 基于经验优化比例-积分控制器 | Kp=1.935, Ki=0.059 | |
| 50% 负荷 |
基于改进灰狼算法优化自抗扰控制器 | β1=193.58, β2=189.14, β3=41.4, k1=100, k2=60, b0=0.2 |
| 基于经验优化自抗扰控制器 | β1=30, β2=100, β3=12, k1=15, k2=80, b0=0.5 | |
| 基于经验优化比例-积分控制器 | Kp=0.24, Ki=0.011 |
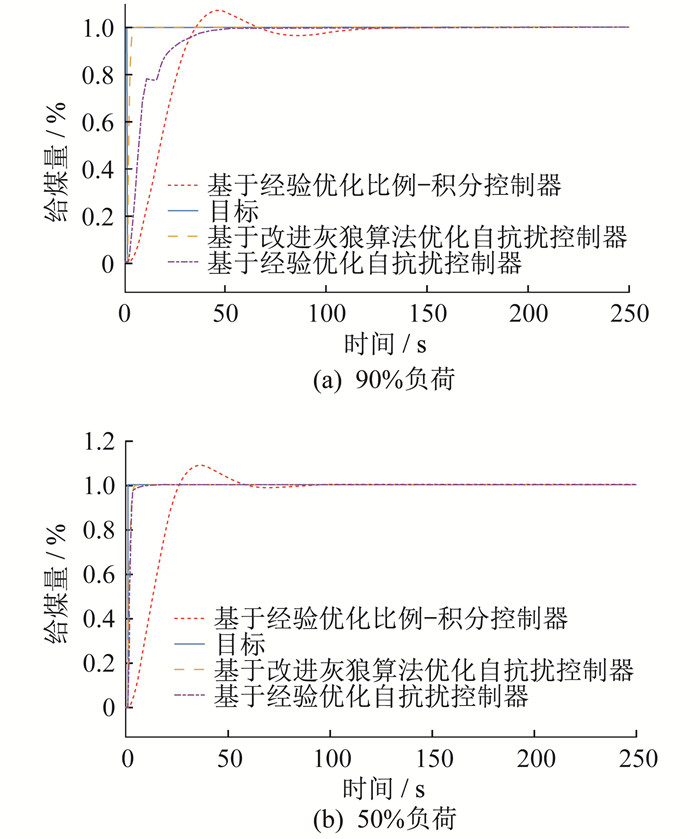
3.3.1 阶跃响应仿真分析
本文以50%负荷和90%负荷为例, 针对火电燃料控制系统采用3种不同控制方式进行仿真实验。时域性能指标如表 3所示。
表 3
时域性能指标
| 工况 | 控制器 | 调节时间/s | 超调量/% |
| 90% 负荷 |
基于改进灰狼算法优化自抗扰控制器 | 3.559 | 0.1 |
| 基于经验优化自抗扰控制器 | 64.399 | 0 | |
| 基于经验优化比例-积分控制器 | 174.757 | 7.1 | |
| 50% 负荷 |
基于改进灰狼算法优化自抗扰控制器 | 5.396 | 0 |
| 基于经验优化自抗扰控制器 | 13.770 | 0 | |
| 基于经验优化比例-积分控制器 | 91.555 | 8.6 |
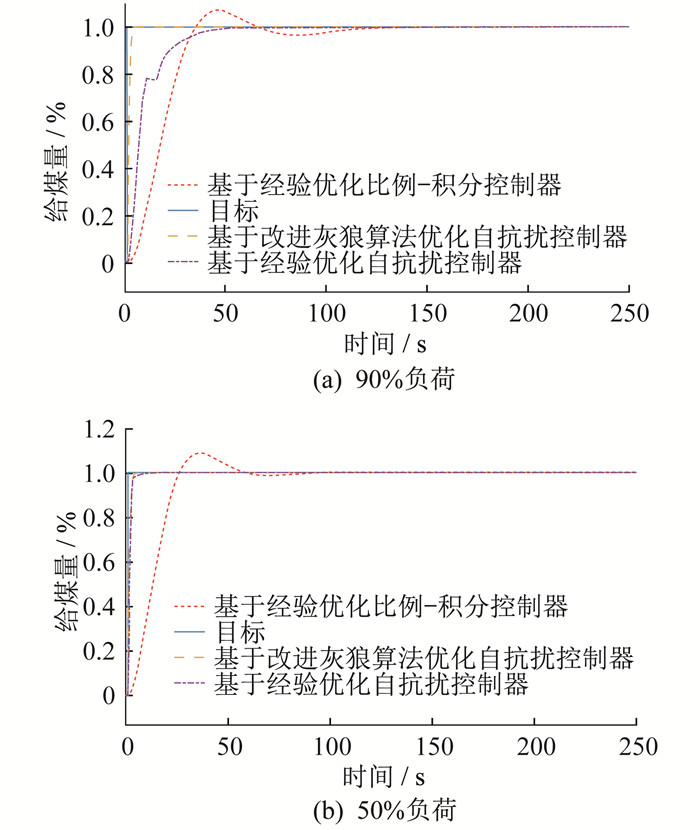
阶跃响应仿真曲线如图 4所示。
由表 3和图 4可知, 在50%负荷下, 采用基于改进灰狼算法优化的自抗扰控制器系统调节时间仅为5.396 s, 比经验整定的自抗扰控制器缩短了60.81%, 比经验整定的比例-积分控制器缩短了94.1%。在90%负荷下, 基于改进灰狼算法优化的自抗扰控制器调节时间为3.559 s, 比经验整定的自抗扰控制器缩短了94.47%, 比比例-积分控制器缩短了97.96%。由此可知, 基于改进灰狼算法优化的自抗扰控制器能更有效实现燃料量的快速、稳定调节, 相较于其他两种控制器具有更好的控制效果。
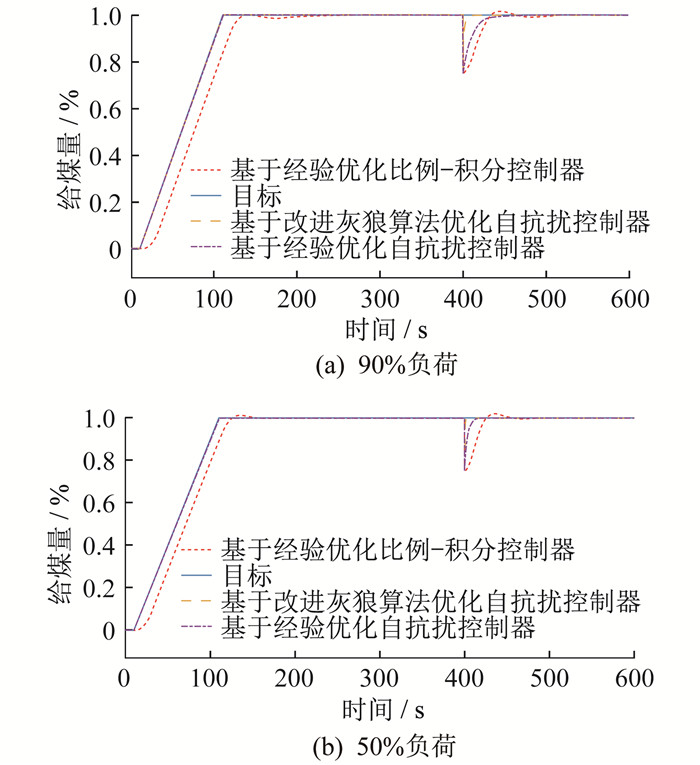
3.3.2 扰动控制仿真分析
为验证基于改进灰狼算法优化自抗扰控制器的抗扰动能力, 在斜坡信号输入作用下, 分别在2种不同负荷下对3种优化方法进行扰动测试, 400 s时在被控对象后加入幅值为0.25的阶跃扰动信号, 以模拟给煤机出现堵煤断煤等情况。阶跃扰动作用下的斜坡响应仿真曲线如图 5所示。
在被控对象前加入平均幅值为3%的随机白噪声扰动信号, 以模拟给煤机工作环境的电磁干扰。在这种情况下斜坡响应仿真曲线如图 6所示。
由图 5和图 6可知, 自抗扰控制器在控制精度上明显优于比例-积分控制器, 在出现扰动信号后可以快速调整达到设定值。在部分工况下, 白噪声扰动信号使比例-积分控制器响应波动较大, 而基于改进灰狼算法优化的自抗扰控制器抗干扰能力更强。
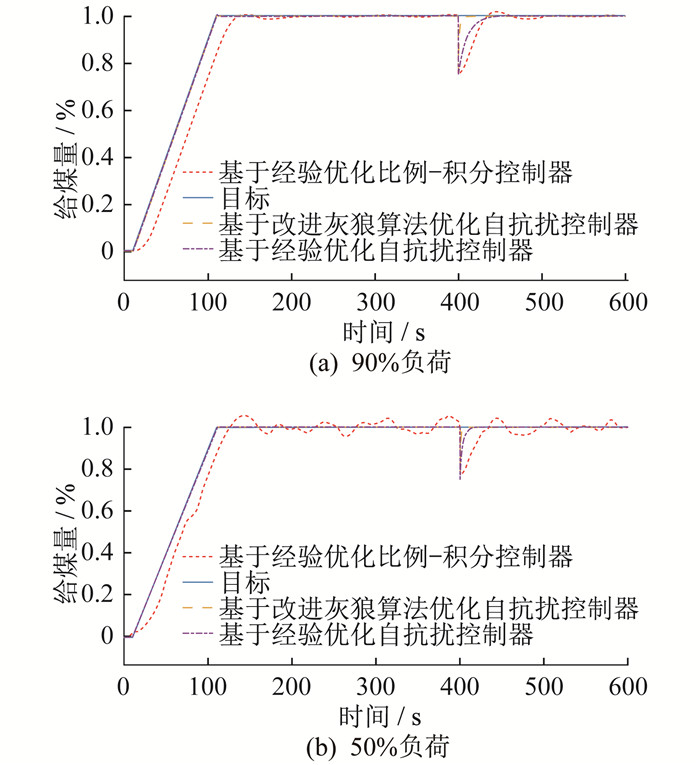
3.3.3 鲁棒性实验仿真分析
为验证基于改进灰狼算法优化的自抗扰控制器的鲁棒性, 将两种工况下被控对象的增益常数和延迟时间均增大10%。在300 s后加入燃料量设定值的阶跃信号, 幅值为0.25, 并在500 s后加入幅值信号为0.1的阶跃扰动信号。在不同工况下鲁棒性实验仿真曲线如图 7所示。
由图 7可知, 基于改进灰狼算法优化的自抗扰控制器在两种负荷下均可实现稳定控制。在90%负荷下, 调节时间为9.48 s, 超调量为0.2%;在50%负荷下, 调节时间为5.393 s, 无超调量, 控制效果均强于其他两种控制方式。在系统500 s时受到扰动后, 3种控制方式均可以恢复到稳定状态。在90%负荷下, 恢复时间为509.68 s; 在50%负荷下恢复时间为502.7 s, 均强于其他两种控制方式。综上所述, 基于改进灰狼算法优化的自抗扰控制器具有较强的鲁棒性。
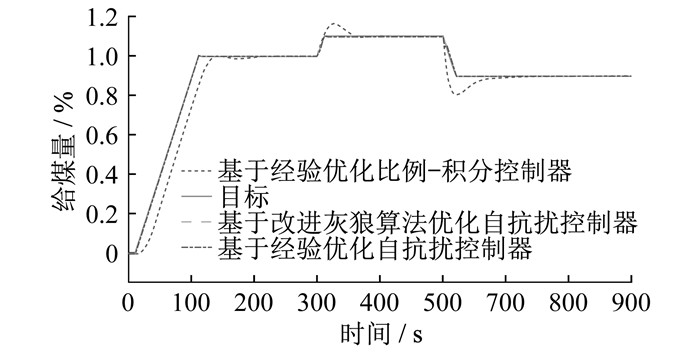
3.3.4 系统变工况仿真分析
为验证基于改进灰狼算法优化的自抗扰控制器面对因变工况而引起的模型变化的适应能力, 以90%负荷为初始条件, 在300 s和500 s连续变工况, 3种控制方式仿真曲线如图 8所示。
由图 8可知, 相较于自抗扰控制器, 比例-积分控制器在变工况下, 实际燃料量发生大幅变化, 超调量和调节时间明显增大。由此可知, 比例-积分控制很难适应系统在不同工况的变化; 而基于改进灰狼算法优化的自抗扰控制器和经验公式整定的自抗扰控制器在变工况运行中可以实现燃料量的快速稳定调节。基于改进灰狼算法优化的自抗扰控制器在变工况运行中实现零超调, 调节时间也快于经验公式整定的自抗扰控制器。因此, 基于改进灰狼算法优化的自抗扰控制器在燃料控制系统变工况运行中具有更好的跟踪能力, 控制效果更好。
4 结语
针对传统的控制器对火电燃料控制系统控制效果不佳的问题, 本文对灰狼优化算法进行改进并对自抗扰控制器的参数进行寻优。在不同工况下进行阶跃响应仿真实验、扰动控制仿真分析实验、鲁棒性实验和变负荷仿真实验。实验结果表明, 相较于传统的控制器, 本文提出的改进灰狼优化算法自抗扰控制器可以更好地实现火电燃料量的快速稳定调节, 具有更好的动态特性, 可以更有效克服内外扰动对系统的影响, 鲁棒性更强, 在变工况过程中也具有更有效的调节效果。
参考文献
-
[1]席裕庚, 李德伟, 林姝. 模型预测控制——现状与挑战[J]. 自动化学报, 2013, 39(3): 222-236.
-
[2]蔚东晓, 贾霞彦. 模糊控制的现状与发展[J]. 自动化与仪器仪表, 2006(6): 4-7.
-
[3]韩京清. 从PID技术到"自抗扰控制"技术[J]. 控制工程, 2002(3): 13-18. DOI:10.3969/j.issn.1671-7848.2002.03.003
-
[4]李杰, 齐晓慧, 万慧, 等. 自抗扰控制: 研究成果总结与展望[J]. 控制理论与应用, 2017, 34(3): 281-295.
-
[5]史永丽, 侯朝桢, 苏海滨. 基于粒子群优化算法的自抗扰控制器设计[J]. 系统仿真学报, 2008(2): 433-436.
-
[6]朱丽玲, 于希宁, 刘磊, 等. 基于遗传算法的ADRC参数整定及其应用[J]. 仪器仪表用户, 2005(4): 64-66.
-
[7]齐晓慧, 李杰, 韩帅涛. 基于BP神经网络的自适应自抗扰控制及仿真[J]. 兵工学报, 2013, 34(6): 776-782.
-
[8]孙立, 董君伊, 李东海. 基于果蝇算法的过热汽温自抗扰优化控制[J]. 清华大学学报(自然科学版), 2014, 54(10): 1288-1292.
-
[9]任丽娜, 吕明月, 王振臣. 改进蜂群算法在风机变桨距控制中的应用[J]. 机械设计与制造, 2015(3): 43-46.
-
[10]张晓凤, 王秀英. 灰狼优化算法研究综述[J]. 计算机科学, 2019, 46(3): 30-38.
-
[11]韩京清. 自抗扰控制器及其应用[J]. 控制与决策, 1998(1): 19-23.
-
[12]吴猛, 朱喜林, 鄂世举, 等. 自抗扰控制器参数整定方法的研究[J]. 北京理工大学学报, 2009, 29(2): 121-123.
-
[13]郭振洲, 刘然, 拱长青, 等. 基于灰狼算法的改进研究[J]. 计算机应用研究, 2017, 34(12): 3603-3606.
-
[14]徐峰, 李东海, 薛亚丽. 基于ITAE指标的PID参数整定方法比较研究[J]. 中国电机工程学报, 2003, 23(8): 207-211.