等离子体是将气体状态的物质解离成负离子、电子、受激原子、溶解原子、自由基、亚稳态原子和中性原子^[1-6]。这些活化物质有较好的化学活性和选择性, 增加化学反应速率, 促进化学反应的进行^[7], 缩短反应时间, 降低能耗, 在生物医学、材料处理、能源转换以及环境治理等领域具有重要的应用前景^[8]。

YOSHINORI I等人^[9]在微波辐照活性焦形成微波等离子体还原NO的过程中, 发现反应器中产生微波等离子体放电现象。文献[10-12]在研究微波辐照碳基材料脱除烟气污染物时, 发现强烈的微波等离子体放电现象, 但对于影响微波等离子体形成的因素研究尚不明确。

微波等离子体的形成是通过电场强化效应实现的, 在多相微波辐照系统中, 介质相中的电场强度理论上是空气中电场强度的ε′倍。当粒子间隙中的最大电场强度大于介质相中电场强度的ε′倍时, 称为电场强化效应^[13]。电场强化效应主要可以归结为3个方面: 表面波、形貌共振、几何学因素。

SUGAI H等人^[14]研究发现当微波的入射角小于介质界面的临界入射角时, 微波可以穿过介质层, 使得气体中的自由电子获得足够高的电场能量从而产生表面波等离子体。彭飞^[15]研究发现电磁波穿过介质后可以通过体积波或表面波的方式在腔体中传播, 足够强度的表面波可以在具有低气压腔体中激发等离子体, 激发的等离子体可以继续维持表面波的传输。陈传杰^[16]研究了微波辐照在管表面形成表面波等离子体产生放电的现象, 发现等离子体是由表面波产生和维持的, 而表面波的传播和约束需要等离子体, 通过这样相互依赖的特殊方式将维持等离子体的电磁波都约束在等离子体管的附近。

HAMZA K K等人^[17]研究了在微波辐照情况下, 通过用形貌共振理论来解释家用微波炉中的葡萄与葡萄形成等离子体的现象, 发现在葡萄间隙间形成微波共振腔, 微波在交界处交叠, 孤立球体中的共振会相互叠加, 从而使葡萄在接触点处显示出强烈的热点, 足以使可用的钠和钾离子电离, 从而点燃等离子体。

BIRNBOIM A等人^[18]在ZnO-空气系统中, 2个微米级ZnO颗粒颈部区域的电场强度是外加电场的30倍。BOOSKE J H等人^[19]用几何学和相应的方程说明了2个微波烧结陶瓷颗粒边界处的电场增强。刘文超^[20]通过数值模拟研究电场增强因子与T型结构取向和长径比的关系, 发现T型结构中竖直方向针状颗粒才是引起电场增强的关键, 且其取向角越接近0°, 引起的电场强化效应越强, 竖直方向针状颗粒长径比是影响电场增强因子大小的关键, 而水平方向针状颗粒长径比几乎没有影响。

为进一步研究碳基材料对微波等离子体形成的影响因素, 提升微波等离子体在材料处理、能源环境等领域的应用效果, 本文通过COMSOL Multiphysics建立一个将电磁波和固体传热2个模块耦合到一起的模型^[20-24], 对负载球形煤焦颗粒时的电场强度分布和温度变化进行研究。根据电介质吸波理论, 温度是电场强度在单位时间内的积分, 采用非接触式红外热像仪测量煤焦样品的表面温度分布展现该区域内电场强度的分布情况, 而不是单一地研究微波谐振腔内电场强度或温度变化。最后, 通过数值模拟计算与实验, 系统分析了2个球形煤焦颗粒接触点处的表面法线与电场方向之间的夹角、颗粒粒径以及2个颗粒的间距对电场强化效应的影响。

本文中的数值模拟模型是通过COMSOL Multiphysics来进行构建的, 用有限元方法来求解微波辐照球形煤焦颗粒间的电场强化效应。结合电磁波频域分析计算以及瞬态固体传热模拟, 分析影响球形煤焦颗粒间电场强化效应的因素。

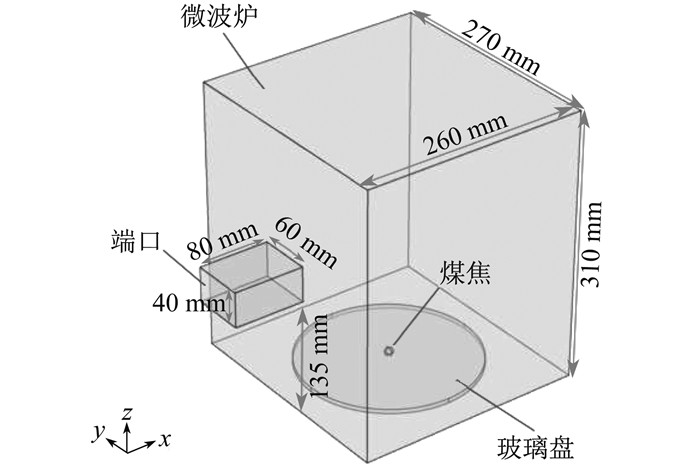
根据实验所用微波炉的尺寸, 建立了微波炉的三维几何模型, 如图 1所示。

微波炉的内壁和波导都是用铜制成的, 腔体通过1个工作在TE₁₀模式下的矩形波导与2.45 GHz微波源相连, 腔体内充满氮气, 底部中央有1个玻璃盘, 上面载有2个半径为5 mm球形煤焦, 改变2个煤焦颗粒接触点处的表面法线和电场方向之间的夹角、颗粒粒径以及2个颗粒的间距, 进行数值模拟研究。

为了简化问题和减少数值模拟计算时间, 对本文的模拟工作作出如下假设^[25]:

(1) 谐振腔和波导用铜(理想电导体)作为壁面材料, 且其厚度可以忽略不计;

(2) 不考虑微波频率的波动;

(3) 所有材料都是均匀非磁性的, 即磁场的相互作用可以忽略;

(4) 氮气和玻璃盘的介电损耗为零, 因此在这些区域内没有发生传热;

(5) 煤焦颗粒为各向同性材料, 且初始温度分布均匀;

(6) 微波加热过程中, 无任何气体吸附、相变和化学反应的发生。

求解麦克斯韦方程或朗伯定律是计算电磁场最常用的方法。文献[26]通过比较模拟和实测的热分布, 发现Maxwell方程比Lambert定律更准确。因此, 本文中电磁场的计算采用频域麦克斯韦方程, 即

$ \nabla \cdot \mu_r^{-1}(\nabla \cdot E)-k_0^2\left(\varepsilon_{\mathrm{r}}-\frac{\mathrm{j} \sigma}{\omega \varepsilon_0}\right) E=0 $

(1)

式中: μ_r——相对磁导率;

E——电场强度, V/m;

k₀——自由空间波数;

ε_r——相对介电常数;

σ——煤焦的电导率, 其值为0.002 S/m;

ω——角频率, rad/s;

ε₀——真空介电常数。

k₀可定义为

$ k_0=\frac{\omega}{c_0} $

(2)

式中: c₀——真空中的光速, m/s。

ε_r可表示为

$ \varepsilon_{\mathrm{r}}=\varepsilon^{\prime}-\mathrm{j} \varepsilon^{\prime \prime} $

(3)

式中: ε′——介电常数, 反映了材料储存电磁能的能力, 其值为5.8;

ε"——损耗因子, 主导着将电磁能转化为热能的能力, 其值为0.72。

当电磁波与介质材料相互作用时, 部分电磁波能量会转化为热量, 电磁波能量损耗Q_e可表示为

$ Q_{\mathrm{e}}=Q_{\mathrm{rh}}+Q_{\mathrm{ml}} $

(4)

$ Q_{\mathrm{rh}}=\frac{1}{2} \operatorname{Re} J E $

(5)

$ Q_{\mathrm{ml}}=\frac{1}{2} R e i \omega B H $

(6)

式中: Q_rh——电阻损耗;

Q_ml——电磁损耗;

J——电流密度, A/m²;

B——磁通量密度, T;

H——电磁场强度, A/m。

在COMSOL软件模型中的传热部分, 以Q_e作为热源。根据计算煤焦的传热条件, COMSOL软件通过傅里叶能量平衡方程将电磁波频域模块与固体传热模块耦合, 其公式为

$ \rho C_{\mathrm{p}} \frac{\partial T}{\partial t}=\nabla \cdot(k \nabla T)+Q_{\mathrm{e}} $

(7)

式中: ρ——密度, kg/m³;

C_p——比热容, J/(kg·K);

T——温度, K;

k——导热系数, W/(m·K)。

在微波炉和矩形波导的壁面上施加了阻抗边界条件, 已知电场只能穿透边界以外的一小段距离, 可表示为

$ \sqrt{\frac{\mu_1 \mu_{\mathrm{r}}}{\varepsilon_0 \varepsilon_{\mathrm{r}}-\frac{\mathrm{j} \sigma}{\omega}} } \boldsymbol{n}\cdot H+E-(\boldsymbol{n} \cdot E) \boldsymbol{n}=\left(\boldsymbol{n} \cdot E_{\mathrm{s}}\right) \boldsymbol{n}-E_{\mathrm{s}} $

(8)

式中: n——单位矢量;

E_S——源电场, 可用于指定边界上的源表面电流, V/m。

电磁波在波导中以特定的模式传播, 这种模式主要是由频率和波导尺寸决定。在本文的研究中, 矩形波导受到横向电(Transeverse Electric, TE)波的激励, 而TE波在传播方向上没有电场分量。不同模式的截止频率v_c由式(9)决定:

$ v_{\mathrm{c}}=\frac{c}{2} \sqrt{\left(\frac{m}{a}\right)^2+\left(\frac{n}{b}\right)^2} $

(9)

式中: c——光速, m/s;

m、n——模式数, TE₁₀模式是2.45 GHz频率下唯一的传播模式, m=1, n=0;

a、b——常数, 对于矩形波导的横截面尺寸a=20 cm, b=10 cm。

端口条件要求传播常数β, 在微波频率v时由式(10)给出:

$ \beta=\frac{2 \pi}{c} \sqrt{v^2-v_{\mathrm{c}}^2} $

(10)

根据COMSOL模型假设, 氮气和玻璃板没有任何损失, 因此传热只发生在球形煤焦颗粒内部。因为球形煤焦颗粒表面没有热流, 所以表面采用绝热边界条件, 在边界上没有温差, 热量不能在边界上传递。

为了验证模拟的正确性, 采用非接触式红外热像仪测量煤焦颗粒的表面温度分布, 根据电介质吸波理论, 温度是电场强度在单位时间内的积分, 电场越强, 温度越高。

对空载时的微波炉进行数值模拟, 得到电场强度E₀为2.5×10⁴ V/m, 定义电场增强因子f为

$ f=\frac{E_{\max }}{E_0} $

(11)

式中: E_max——球形煤焦颗粒间的电场强度最大值。

氮气的击穿电场强度阈值为3.4×10⁵ V/m, 即当电场增强因子f大于13.6时, 可以击穿氮气, 产生放电现象, 形成微波等离子体。

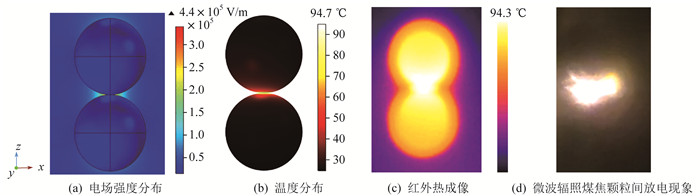
在微波输入功率为800 W的情况下, 谐振腔内充满氮气作为保护气, 微波辐照10 s后, 球形煤焦颗粒的模拟与实验结果如图 2所示。图 2(a)为2个煤焦颗粒的电场强度分布模拟结果, 在2个煤焦颗粒间形成了电场强化效应, 电场强度最大值E_max为4.4×10⁵ V/m, 大于氮气的击穿电场强度阈值, 可以产生放电现象, 形成微波等离子体。由图 2(b)与图 2(c)可以看出, 数值模拟温度分布与红外热成像图吻合结果良好。在实验中观察到了明显的微波等离子体放电现象如图 2(d)所示。以上结果验证了数值模拟模型的正确性。

红外热成像仪成像依赖于球形煤焦颗粒吸收微波后温度的变化, 但该方法对球形煤焦颗粒外部氮气的温度分布不敏感。为进一步验证电场强化效应只发生在球形煤焦颗粒间, 而不存在于球形煤焦颗粒周围的其他地方, 选用热敏纸(厚度为0.08 mm, 在温度约70 ℃时会急剧变暗)进行验证。

利用热敏纸带监测球形煤焦颗粒周围的温度。采用折叠的16层热敏纸垫片监测2个煤焦颗粒之间的电场强化效应。球形煤焦颗粒被微波辐照60 s后, 对热点效应的热敏纸带监测结果如图 3所示。热敏纸可以显示是否超过了温度阈值、煤焦颗粒间的气体是否会被电离形成高温以及周围氮气温度场的信息。

由图 3可知, 实验结果图 3(c)和图 3(d), 与数值模拟结果图 3(b)完全一致。由于煤焦介电性能较小且其尺寸属于毫米级, 且球形煤焦颗粒间距较大, 无法发生共振, 不会在球形煤焦颗粒间形成电离产生高温; 微波先入射到第1个煤焦颗粒内, 颗粒间产生电场强化效应在球形煤焦颗粒的表面形成热点, 导致其出现较高的温度与较大的热点, 在图 3(d)的热敏纸带上从左到右变色范围逐渐减小且颜色逐渐变淡。

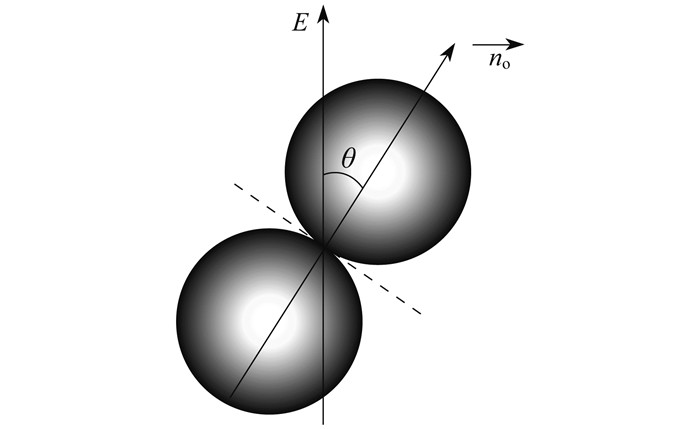
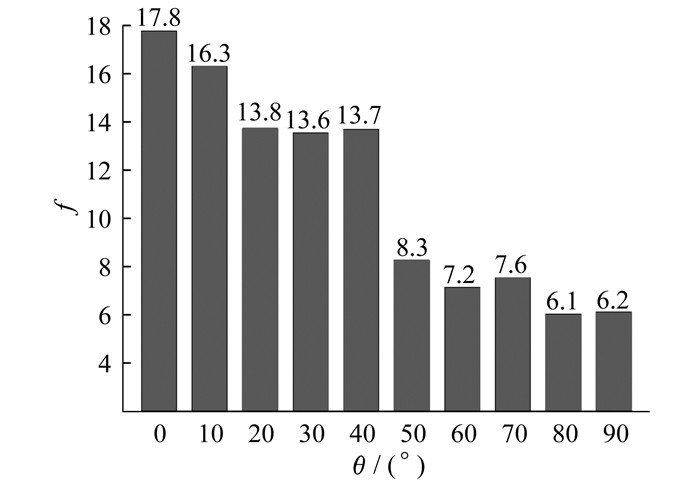
研究夹角对球形煤焦颗粒间电场强化效应的影响, 定义2个球形煤焦颗粒接触点处的表面法线n_o与电场E方向之间的夹角为θ, 如图 4所示。调节夹角θ为0°~90°进行模拟, 可得电场增强因子f随夹角θ的变化过程如图 5所示。

模拟结果表明, 随着夹角θ的逐渐增加, 电场增强因子f逐渐减小, 但最大电场强度始终出现在2个煤焦颗粒的中间, 主要可以分为3个阶段: 第1阶段θ为0°~10°, 电场增强因子f较高, 分别为17.8和16.3, 都可产生强烈的放电现象; 第2阶段θ为20°~40°, f几乎不变, 约等于13.6, 处于放电击穿的临界值; 第3阶段θ为50°~90°, f出现骤降, 降到8.3以下。煤焦是一种介于导体与非导体的材料, 具有一定的导电性能, 其表面可以形成表面波等离子体, θ从40°~50°时, 微波的入射角达到了煤焦界面的临界入射角, 导致微波不能穿过煤焦, 电场能量不能在2个煤焦颗粒间的接触点周围被强烈聚集, 电场强化效应减弱, 不会产生放电现象, 因此不能形成等离子体。这也验证了BIRNBOIM A等人^[18]的研究, 2个微米尺度陶瓷球中的电场强度是由电场方向和2个球的接触点处的表面法线之间的夹角决定的, 当夹角从0°增加到90°时, 电场强化效应随之减弱。由以上分析可以看出, 当2个球形煤焦颗粒间接触点处的表面法线和电场方向之间的夹角θ=0°时, 电场强化效应最强且增强位置发生在2个介质球的接触点处, 将有助于碳基材料的非等温加热和“热点”的出现。球形煤焦颗粒间隙中微波的增强电场能量比煤焦颗粒内部高一个数量级, 对增强局部电场有积极作用, 能够在煤焦颗粒间击穿氮气产生放电形成微波等离子体。

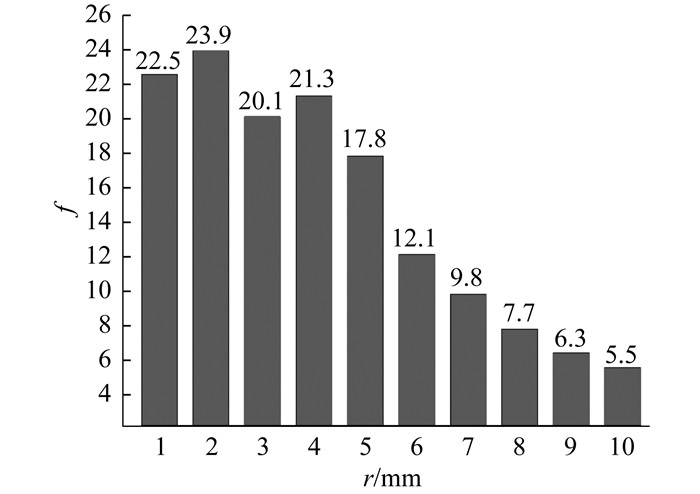
为了研究粒径对球形煤焦颗粒间电场强化效应的影响, 选用半径r为1~10 mm的球形煤焦颗粒进行模拟, 结果如图 6所示。

由图 6可知, 以氮气的击穿电场强度阈值(即f =13.6)为分界线。当煤焦颗粒半径r不大于5 mm时, 电场增强因子f均大于13.6, 说明此时煤焦颗粒表面的电磁波会在接触点处发生聚集, 产生放电现象形成微波等离子体; 当煤焦颗粒半径r大于5 mm时, 电场增强因子f均小于13.6, 说明此时不会产生放电现象。

煤焦粒径对电场强化效应的影响是由微波在煤焦内的穿透深度所决定的。穿透深度是微波在介质中穿透深度的量度, 当介质半径r不大于5 mm时, 微波可以完全穿过煤焦颗粒与辐照到煤焦颗粒表面的电磁波进行叠加, 形成电场强度的区域较大, 使得电场强化效应增加, 产生放电现象形成微波等离子体。电场增强因子f在介质半径5~6 mm时发生了骤降, 主要原因是微波的穿透深度对煤焦颗粒间的电场强度起了决定性作用, 由于煤焦粒径的增大, 微波在煤焦颗粒内损耗增加, 使得微波不能穿越煤焦颗粒, 产生的电场强化效应变弱。

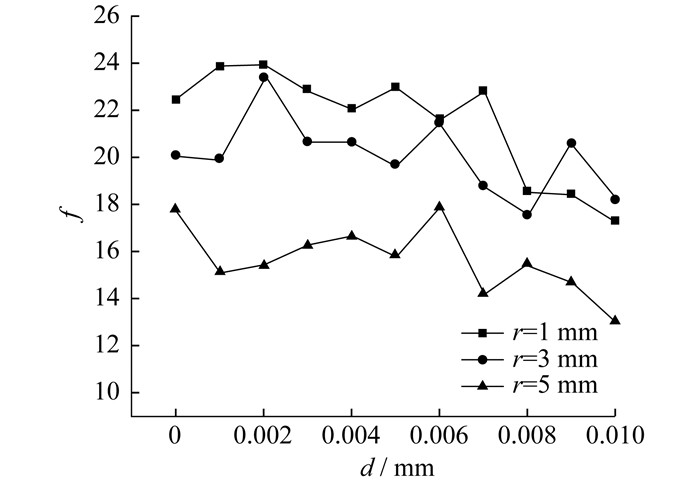
研究2个球形煤焦颗粒间距对煤焦颗粒间电场强化效应的影响。选用间距d为0~0.01 mm的球形煤焦颗粒进行数值模拟, 模拟结果如图 7所示。

由图 7可知, 通过数值模拟研究表明球形煤焦颗粒间的小间距而不是无间距是电场强化效应的最佳条件。半径为1 mm的球形煤焦颗粒间最强的电场强化效应发生在间距为0.001 mm和0.002 mm时; 半径为3 mm发生在间距为0.002 mm时; 半径为5 mm发生在间距为0.006 mm时。微波辐照球形煤焦颗粒时, 微波和球形煤焦颗粒之间会发生相互作用, 当颗粒的间距变小时, 电磁波会集中分布于2个煤焦颗粒之间并形成共振, 聚集于球形煤焦颗粒间的表面之上, 产生电场强化效应; 当球形煤焦颗粒间的间隙与尺寸之比增加, 颗粒间的共振现象消失, 导致球形煤焦颗粒表面的微波损耗增加, 在煤焦颗粒间产生衰减, 与空间内的电磁波不能在间距处相互叠加, 能量不能在2个球的接触点周围被强烈聚集, 电场强化效应减弱。产生这种现象, 主要是与球形煤焦颗粒的介电常数有关。介电常数较大的物质, 间距大小对电场强化效应有很大的影响, 但煤焦属于低介电常数的物质, 几何学因素是影响电场强化效应的关键因素。

本文建立了微波加热煤焦的电磁波频域-固体传热耦合模型, 通过对2个球形煤焦颗粒(毫米级)接触点处的表面法线和电场方向之间的夹角、颗粒粒径以及2个颗粒的间距进行了数值模拟研究与实验验证, 具体结果如下。

(1) 数值模拟与实验结果吻合良好, 电场强化效应总是发生在2个煤焦颗粒的接触点处, 在煤焦颗粒间观察到了明显的微波等离子体放电现象。

(2) 夹角θ的增加使得电场增强因子f逐渐减小。夹角θ的改变会导致微波的入射角发生变化, 当夹角θ为0°时, 电场强化效应最强; f会在夹角θ从40°增加到50°时出现骤降, 是因为微波的入射角达到了煤焦界面的临界入射角。

(3) 电场增强因子f在煤焦颗粒半径为5~6 mm时发生骤降, 主要原因是微波在煤焦颗粒内的穿透深度对煤焦颗粒间电场强度起决定性作用。随着煤焦颗粒粒径的增大, 微波在煤焦颗粒内损耗增加, 使得微波不能穿越煤焦颗粒, 导致电场强化效应减弱。

(4) 毫米级球形煤焦颗粒间的小间距而不是无间距是电场强化效应的最佳条件, 这是由于煤焦属于低介电常数的物质, 几何学因素是影响电场强化效应的关键因素。