|
|
|
发布时间: 2023-02-28 |
清洁安全发电 |
|
|
|
收稿日期: 2022-02-11
基金项目: 国家自然科学基金(5197632);山西省基础研究计划项目(202203021211167)
中图法分类号: TK124
文献标识码: A
文章编号: 2096-8299(2023)01-0054-07
|
摘要
基于流体体积(VOF)模型对恒定热流密度下的微圆柱阵通道内的流动沸腾换热特性展开数值研究, 并利用几何重构法捕捉气液两相界面迁移变化, 研究了流道内流速的分布和微圆柱高度对气泡分布、沸腾换热性能及沸腾不稳定性的影响。结果表明: 微圆柱的存在增加了气泡核化点密度; 气泡运动增加了工质与加热壁面接触的可能性; 微圆柱高度较低时, 易发生气塞现象, 加热面散热不均导致局部异常过热, 换热性能下降; 微圆柱阵通过阻碍气泡反向流动来降低沸腾不稳定性, 但微圆柱高度过高会造成换热系统振荡, 影响传热可靠性。
关键词
微圆柱阵; 微通道; 沸腾换热; 气液两相流; 气泡
Abstract
The heat transfer characteristics of flow boiling in the cylindrical micro-fin channel with constant heat flux at the bottom were numerically studied, which was based on the VOF flow model coupled with boiling heat and mass transfer model.To capture the movement of vapor-liquid interface by the geo-reconstruction method, this article studied the partial velocity variation of two-phase interface.Simultaneously, it analyzed the effect of rib height on the morphology of bubbles, flow boiling heat transfer characteristics and boiling instability in the micro-channel.The results show that the presence of micro-columns increases the density of bubble nucleation point.The bubbles movement increases the possibility of contact between working medium and heating wall.When the height of rib is low, the capillary force generated by the secondary channel is weak and air bubbles are not easy to escape.This can lead to locally abnormal overheating and cause the heat transfer to deteriorate.Reversing flow of the bubbles is blocked by micro-fin array, and the boiling instability is reduced.However, over-hight micro-fin can lead to oscillate heat transfer system, thus affecting the reliability of heat transfer.
Key words
micro-rib structure; micro-channel; boiling heat transfer; vapor-liquid two-phase flow; air bubbles
微通道散热器具有可靠运行、微型化和高能效的优势[1], 在农业、航空航天、太阳能等领域得到广泛应用。随着技术的不断发展, 急剧增加的热负荷使设备的安全性和寿命受到挑战, 因此迫切需要高效的散热手段。TUCKERMAN D B等人[2]在30多年前提出的微通道沸腾换热可以有效解决该问题, 即液体通过吸收大量热量生成气泡从而有效增强换热性能。
目前, 已有很多学者在微通道沸腾两相流领域展开了研究。文献[3]研究发现, 相比常规尺寸管, 过冷液体在微通道中流动沸腾的传热特性和冷却性能有较大提高。文献[4-5]在微通道流动沸腾实验中观察到气泡的多种流型, 同时发现流型转变会影响沸腾换热性能和传热不稳定性。段芮等人[6]通过实验观察到对于翅片较密的沸腾管, 排液能力较差会导致换热系数不佳。LIU H等人[7]利用高速摄像捕捉气泡运动轨迹, 发现较高热通量会导致气泡滑动速度更高且气泡间更易合并。KRISHNAMURTHY S等人[8]通过微针肋通道的沸腾换热实验发现, 与光滑平面相比, 微针肋表面的流动沸腾换热显著增强, 且两相传热系数与质量流量、热流密度均无关。HUA J Y等人[9]研究了微通道沸腾的传热特性与气泡动力学特性的内在联系, 从气泡出现的数量和顺序等角度分析三角形针翅具有较高传热系数的原因。LEE W等人[10]通过沸腾模拟计算发现, 锥形空腔表面微结构加速了气泡的生长和脱离进程, 有效提高了沸腾换热性能。LIN Y H等人[11]模拟研究了平行微通道2个单气泡的生长, 发现增加质量通量能够抑制气泡流动逆转, 降低沸腾不稳定性。PRAJAPATI Y K等人[12]对分段翅片微通道沸腾过程进行了数值研究, 结果表明, 二次通道的存在使气泡的生长速度更快, 换热系数更高。陈宏霞等人[13]采用流体体积(Volume of Fluid, VOF)模型模拟研究了微肋表面单个气泡的动力特性, 表明微肋结构对于气泡的生长和脱离具有明显的促进作用。KIM J S等人[14]研究了水平管沸腾生成的气泡形核位置分布和气泡行为, 采用新型热分配模型更加真实地反映了气泡滑动现象。LI X L等人[15]模拟研究了圆柱微通道内液滴的两相流传热, 发现随着滑移长度的增加, 液滴两相流中的传热效果也会增强。
综上所述, 对于微通道沸腾换热的研究主要基于整体宏观方面, 而由于微结构的复杂性, 目前对局部微观的沸腾换热研究尚少, 因此本文对圆形微圆柱阵通道内的流动沸腾过程进行数值模拟, 通过捕捉气液相界面的运动行为, 研究分析局部气泡运动特性, 分析微圆柱高度对微通道内气泡分布、沸腾换热特性及沸腾不稳定性的影响, 以期为散热器的结构优化提供思路。
1 物理模型
1.1 几何模型
1.2 控制方程
本文做出以下假设: 水和水蒸气为不可压缩流体; 水和水蒸气在饱和压力及温度下的物性参数为常数; 通道尺寸过小, 不考虑重力影响。
VOF模型通过求解一组动量方程, 并跟踪整个计算域中气液两相的体积分数来对两相进行建模, 能够更加精确地追踪气液相界面。VOF模型的建立基于以下条件: 2种或多种流体(或相)不互溶, 则液相和气相体积分数的总和应当保持恒定, 即
| $ \alpha_{\mathrm{l}}+\alpha_{\mathrm{v}}=1 $ | (1) |
式中: αl、αv——液相、气相的体积分数。
基于VOF模型的液相和气相的连续性方程为
| $ \frac{\partial \alpha_{\mathrm{l}}}{\partial t}+\nabla \cdot\left(\boldsymbol{v} \alpha_{\mathrm{l}}\right)=-\frac{S}{\rho_{\mathrm{l}}} $ | (2) |
| $ \frac{\partial \alpha_v}{\partial t}+\nabla \cdot\left(\boldsymbol{v} \alpha_v\right)=-\frac{S}{\rho_v} $ | (3) |
式中: t——时间, s;
v——气液两相的平均速度, m/s;
S——液相转移到气相的质量源项, kg;
ρl、ρv——液体密度和气体密度, kg/m3。
动量方程为
| $ \begin{aligned} & \frac{\partial(\rho \boldsymbol{v})}{\partial t}+\nabla \cdot(\rho \boldsymbol{v} \boldsymbol{v})=-\nabla p+ \\ & \nabla \cdot\left[\mu\left(\nabla \boldsymbol{v}+\nabla \boldsymbol{v}^{\mathrm{T}}\right)\right]+\rho g+F_{\mathrm{vol}} \end{aligned} $ | (4) |
式中: ρ——混合相的密度, kg/m3;
p——气液相界面的局部压力, Pa;
μ——混合相动力黏度, Pa·s;
g——重力加速度;
Fvol——体积力, N。
气泡与微通道尺寸处于同一量级, 因此气泡所受表面张力[16]对于沸腾流动是非常重要的影响因素。将表面张力作为体积力加入动量方程中, 其形式为
| $ F_{\mathrm{vol}}=\sigma \frac{\rho \kappa_{\mathrm{l}} \nabla \alpha_{\mathrm{l}}}{0.5\left(\rho_{\mathrm{l}}+\rho_{\mathrm{v}}\right)} $ | (5) |
式中: σ——表面张力系数, N/m;
κl——两相界面的液相曲率。
由于温度变化幅度较小, 表面张力采用常数, 数值取0.059。
能量方程为
| $ \begin{gathered} \frac{\partial(\rho E)}{\partial t}+\nabla \cdot[\boldsymbol{v}(\rho E+p)]= \\ \nabla \cdot(\lambda \nabla T)+Q \end{gathered} $ | (6) |
式中: E——气液两相流体的内能, J/kg;
λ——气液两相的导热系数, W/(m·K);
T——气液两相共用的温度, K;
Q——通过界面的体积能量源项, J/kg。
沸腾换热需要考虑质量和能量在气液两相界面处的传递。质量传递取决于局部温度和饱和温度之间的温差, 如果局部温度高于饱和温度, 就会发生沸腾, 液相质量转移到气相, 否则会发生凝结。因此, 质量源项[17]为
| $ S= \begin{cases}\frac{r_{\mathrm{l}} \alpha_{\mathrm{l}} \rho_{\mathrm{l}}\left(T_{\mathrm{l}}-T_{\mathrm{sat}}\right)}{T_{\mathrm{sat}}}, & T_{\mathrm{l}} \geqslant T_{\mathrm{sat}} \\ \frac{r_{\mathrm{v}} \alpha_{\mathrm{v}} \rho_{\mathrm{v}}\left(T_{\mathrm{l}}-T_{\mathrm{sat}}\right)}{T_{\mathrm{sat}}}, & T_{\mathrm{l}}<T_{\mathrm{sat}}\end{cases} $ | (7) |
式中: rl、rv——液相和气相的质量传递强度因子, 取1 s-1;
Tl、Tsat——液体的温度和饱和温度, K。
| $ Q=-h_\text{lv}S $ | (8) |
式中: hlv——液相传递到气相的潜热, J/kg。
模拟计算中, 质量源项和能量源项通过用户自定义函数与VOF模型进行耦合。
1.3 网格划分及网格无关性验证
1.4 边界条件
微通道内沸腾换热的边界条件设置如下: 入口边界, 速度v=0.4 m/s, 温度T1=370 K; 出口边界, 压力出口处的回流温度T2=373.15 K; 流体区边界, 上边界及四周边界均为绝热边界; 固体区边界, 加热底面为恒定热流密度ρ0=300 kW/m2; 基底板侧壁面均为绝热壁面。
求解方法采用PISO算法和几何重构法, 模拟计算的时间步长取1.0×10-7s。
2 数值模拟结果与分析
2.1 模型验证
为了验证模型的可行性, 对三维矩形平直微通道内的流动沸腾换热进行模拟, 与文献[21]中参数设置一致, 计算3组入口流速下的流动沸腾换热系数, 并与文献[21]中的模拟值和实验值进行比较, 结果如表 2所示。
| 入口速度/(m·s-1) | 沸腾换热系数/[W·(m2·K)-1] | 误差/% | ||||
| 计算值 | 模拟值 | 实验值 | 模拟误差 | 实验误差 | ||
| 0.10 | 87 358 | 84 927 | 78 146 | 2.9 | 11.8 | |
| 0.15 | 86 462 | 85 189 | 78 613 | 1.5 | 9.9 | |
| 0.20 | 88 205 | 85 831 | 79 275 | 2.7 | 11.3 | |
其中, 误差的计算公式为: 误差=(模拟结果-文献结果)/文献结果。由表 2可以得出, 本文计算结果与文献[21]模拟值的平均误差为2.4%, 与实验值平均误差为11.0%, 吻合程度良好, 证明本文所采用的VOF模型及传热传质模型是合理可靠的。
2.2 模拟结果与分析
2.2.1 气泡动力特性分析
l=0.1 mm、t=40 ms时的微通道内气泡分布云图如图 2所示, 蓝色部分为气泡。
由图 2可以看出, 通道入口段气泡较少, 这是因为入口处流体不断冲刷加热壁面使气泡脱离; 小气泡主要集中在微圆柱周围, 这是由于微圆柱的存在提供了大量的气化核心, 有助于气泡的生成; 通道出口段多为大气泡, 这是因为从加热面上脱离的气泡随着流动方向(沿x正方向)汇集在通道尾端, 小气泡聚并成气泡块, 堵塞通道。
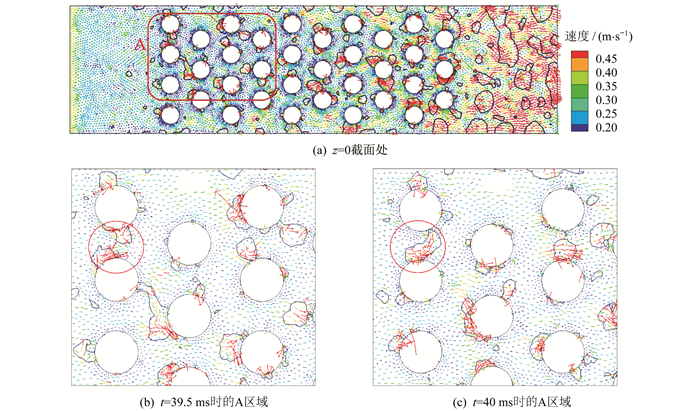
l=0.05 mm、t=39.5 ms时, 微通道内流体的速度矢量图如图 3所示。由图 3可以看出, 3~13 mm处布置有微圆柱阵, 流体阻力作用增大, 微圆柱周围流体速度骤降至0.2 m/s以下, 整体流速偏低; 在x=13 mm处流体进入平直通道, 速度提高至0.45 m/s以上。图 3(b)和图 3(c)是图 3(a)内方框区域A的放大图, 可以看出气液两相界面处流体速度远大于周围, 微圆柱间气泡发生聚并现象。t=39.5 ms时2个气泡分别生长在相邻的微圆柱上, t=40 ms时气泡发生合并, 且速度沿着合并的方向加大。这是由于随着气泡的生长、聚并, 其体积不断膨胀, 推动流体流动。同时, 由于微通道尺寸过小, 气泡与微通道处于相同量级, 对流体的扰动更加剧烈。这个现象说明, 气泡运动是影响通道内部流速变化的主要因素之一。
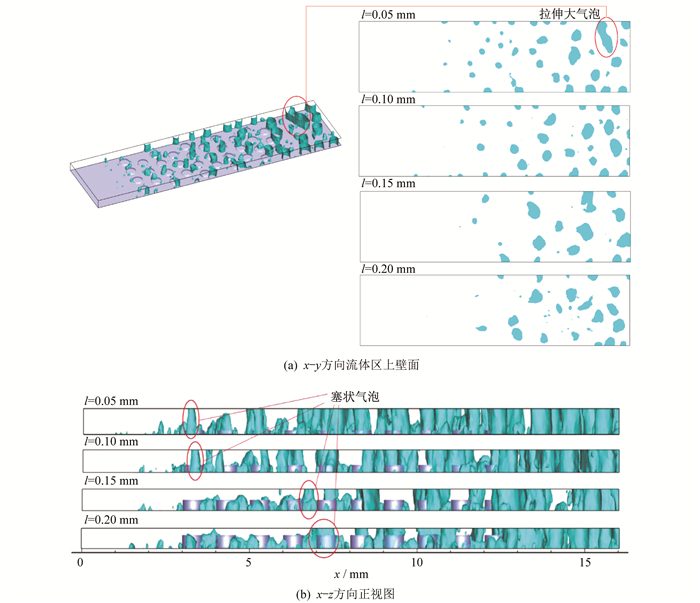
不同微圆柱高度下微通道内的沸腾现象图片如图 4所示。4组微通道皆出现了许多贯通整个通道高度方向的塞状气泡。图 4(a)是流体区上壁面截面处的气泡分布, 可以看出, l=0.15 mm比l=0.10 mm的微通道内塞状气泡明显减少, l=0.05 mm的微通道内甚至出现了拉伸大气泡。由图 4(b)可以看出, 微圆柱高度的增高推后了塞状气泡出现的位置, 且微圆柱高度越高, 大气泡数量越少。这是因为较高的微圆柱之间形成明显的次级通道, 次级通道内产生的毛细力加快了流体的汇入, 气泡跃离频率增加, 相邻气泡不易合并, 通道可以及时排出气泡, 不易造成气塞现象。
2.2.2 微圆柱高度对沸腾换热性能的影响
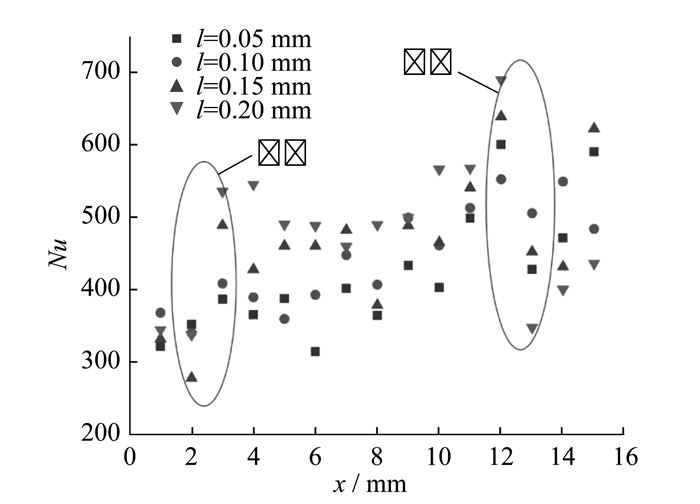
t=40 ms时努塞尔数(Nu)沿流动方向的变化曲线如图 5所示。
图 5中, 0~3 mm处为平直通道, Nu值较小; 3~13 mm布置有微圆柱阵, Nu值明显增大, 并呈现不同程度的波动; 13~16 mm进入平直通道, Nu值大幅减小。结合图 2可知, 由于微圆柱的存在导致生成气泡增多, 次级通道产生的毛细力促进流体汇入, 加快了气泡脱离, Nu值增大, 换热能力增强。同时, l=0.05 mm条件下, x=3 mm比x=2 mm处的Nu值增幅较小, 仅增大了10%;而l=0.20 mm时的Nu值则增大了58%;在微圆柱位置处, l=0.20 mm时的Nu值整体高于其他通道。这是因为微圆柱高度越高, 次级通道产生的毛细力作用越强, 加快了周围流体的汇入, 推动了气泡脱离, 提高了液体与加热面接触的可能性, 增强了换热效率。
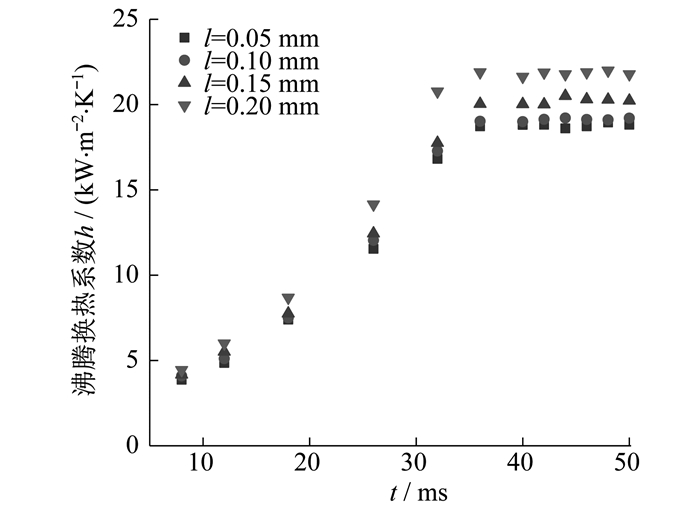
在不同微圆柱高度下, 沸腾换热系数随时间的变化曲线如图 6所示。
由图 6可以看出, 在t=30 ms之后流体完全流过通道, 沸腾换热系数大致趋于稳定, 随着微圆柱高度的增高, 沸腾换热系数逐渐增大。沸腾换热系数h的计算公式为
| $ h=\frac{q_{\mathrm{w}-\mathrm{i}}}{T_{\mathrm{w}-\mathrm{i}}-T_{\mathrm{l}}} $ | (9) |
式中: qw-i——通过固液界面的面积加权平均热通量, kW/m2;
Tw-i——固液界面的面积加权平均温度, K;
Tl——流体的质量加权温度, K。
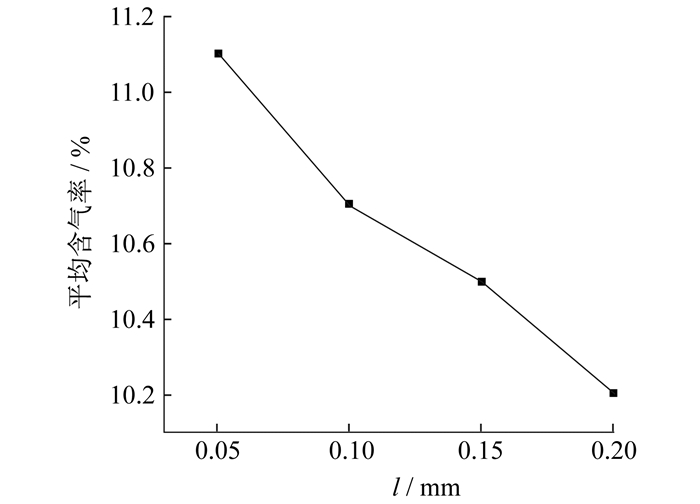
平均含气率随微圆柱高度的变化曲线如图 7所示。其中, 平均含气率取微通道在40~50 ms间含气率的平均值。随着微圆柱高度的增高, 通道含气率减小。结合图 3可知, 由于沸腾过程中气液两相界面的运动增强了流体的扰动, 各处工质实现了与加热面的接触传热, 充分吸收热量, 提高了换热效率, 沸腾换热系数增大, 从而对加热壁面起到显著的降温效果; 微圆柱高度降低, 平均含气率增大, 结合图 4可知, 塞状气泡增多, 堵塞微通道, 使壁面出现干涸现象, 造成局部异常过热, 以过热高温点为中心向周围壁面扩散热量, 进而影响整个微通道壁面的冷却, 沸腾换热系数减小, 导致传热效果减弱。
2.2.3 沸腾不稳定性分析
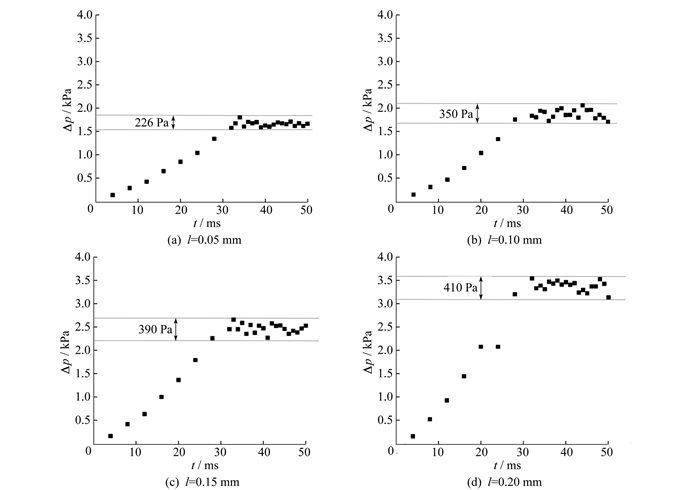
微通道内沸腾产生的气泡易发生反向流动, 会对整个微通道的换热系统造成振荡。流动沸腾不稳定会直接导致提前达到临界热流密度, 致使传热效果减弱, 而微圆柱阵的存在可以有效抑制气泡的反向流动, 提高沸腾的稳定性[22-23]。一般将通道进出口的气液两相压降作为衡量流动是否稳定的标准。不同微圆柱高度下, 进出口压降随时间的变化趋势如图 8所示。在t=30 ms之后流体完全流入微通道, 压降保持在一定范围内的振荡。微圆柱高度进出口压降Δp的波动范围分别为1.58~1.81 kPa(l=0.05 mm), 1.72~2.07 kPa(l=0.10 mm)、2.27~2.66 kPa(l=0.15 mm)、3.14~3.55 kPa(l=0.20 mm)。这表明随着微圆柱高度的增高, 压降也相应增大, 流动沸腾不稳定性升高, 换热系统可靠性降低, 影响了换热器的安全运行。
3 结论
本文对含有微圆柱阵的微通道内流动沸腾的气泡分布规律及流道内速度变化进行了研究, 并分析了微圆柱高度对沸腾换热特性和不稳定性的影响。主要结论如下。
(1) 气液两相界面流体速度大于周围, 次级通道的存在促进了流体的汇入, 加速了气泡脱离, 较少发生气塞现象。
(2) 随着微圆柱高度的增高, 平均含气率减小, 换热系数增大, 换热性能增强。
(3) 微圆柱越高, 进出口流动压降波幅越大, 不稳定性提高, 换热系统振荡明显, 可靠性下降。
参考文献
-
[1]过增元. 当前国际传热界的热点——微电子器件的冷却[J]. 中国科学基金, 1988, 2(7): 20-25.
-
[2]TUCKERMAN D B, PEASE R F W. Corrections to high performance heat sinking for vlsi[J]. IEEE Electron Device Letters, 1981, 2(8): 213-213. DOI:10.1109/EDL.1981.25406
-
[3]PENG X F, WANG B X. Cooling augmentation with microchanneled structures[J]. Journal of Thermal Science, 1993, 2(2): 98-110. DOI:10.1007/BF02718265
-
[4]FAYYADH E M, MAHMOUD M M. Flow boiling heat transfer of R134a in multi-micro-channels[J]. International Journal of Heat and Mass Transfer, 2017(3): 422-436.
-
[5]HUH C, KIM J, KIM M H. Flow pattern transition in a stability during flow boiling in a single micro-channel[J]. International Journal of Heat and Mass Transfer, 2007, 50(5): 1049-1060.
-
[6]段芮, 马虎根, 刘君, 等. 表面增强型强化传热管换热特性实验研究[J]. 上海电力学院学报, 2006, 22(1): 84-88. DOI:10.3969/j.issn.1006-4729.2006.01.021
-
[7]LIU H, CHEN D, QIN J, et al. Visual experimental study on bubble behavior from nucleation site in vertical rectangular channel[J]. Applied Thermal Engineering, 2021, 201: 20-31.
-
[8]KRISHNAMURTHY S, PELES Y. Cross flow boiling in micro-pin fin heat sinks[C]//Asme 2007 International Mechanical Engineering Congress and Exposition, 2007, 10: 11-15.
-
[9]HUA J Y, HOU W X, LI G, et al. The experimental study on the boiling bubble behaviors and heat transfer performance of the deionized water across various pin fins[J]. Heat and Mass Transfer, 2021, 57(10): 1-14.
-
[10]LEE W, SON G, JEONG J J. Numerical analysis of bubble growth and departure from a micro-cavity[J]. Numerical Heat Transfer Part B Fundamentals, 2010, 58(5): 323-342. DOI:10.1080/10407790.2010.522871
-
[11]LIN Y H, LUO Y, LI W, et al. Numerical study of flow reversal during bubble growth and confinement of flow boiling in micro-channels[J]. International Journal of Heat and Mass Transfer, 2021, 177: 121-135.
-
[12]PRAJAPATI Y K, PATHAK M, KALEEM K M. A comparative study of flow boiling heat transfer in three different configurations of micro-channels[J]. International Journal of Heat and Mass Transfer, 2015, 85(2): 711-722.
-
[13]陈宏霞, 孙源, 肖红洋, 等. 微柱结构表面核态沸腾单气泡的数值模拟[J]. 化工进展, 2019, 69(12): 4979-4989.
-
[14]KIM J S, CHO H K. Advanced boiling heat transfer model for a horizontal tube with numerical analysis of bubble behaviours[J]. International Journal of Heat and Mass Transfer, 2021, 175: 121-135.
-
[15]LI X L, HE L Q, QIAN P, et al. Heat transfer enhancement of droplet two-phase flow in cylindrical micro-channel[J]. Applied Thermal Engineering, 2021, 11: 64-74.
-
[16]BRACKBILL J U, KOTHE D B, ZEMACH C. A continuum method for modeling surface tension[J]. Journal of Computational Physics, 1992, 100(2): 335-354. DOI:10.1016/0021-9991(92)90240-Y
-
[17]DING S T, LUO B, LI G. A volume of fluid based method for vapor-liquid phase change simulation with numerical oscillation suppression[J]. International Journal of Heat and Mass Transfer, 2017(3): 348-359.
-
[18]YANG Z, PENG X, YE P. Numerical and experimental investigation of two phase flow during boiling in a coiled tube[J]. International Journal of Heat and Mass Transfer, 2008, 51(5/6): 1003-1016.
-
[19]WEI J, PAN L, CHEN D, et al. Numerical simulation of bubble behaviors in subcooled flow boiling under swing motion[J]. Nuclear Engineering and Design, 2011(8): 2898-2908.
-
[20]ZHOU Z, SHI J, CHEN H H, et al. Two-phase flow over flooded micro-pillar structures with engineered wettability pattern[J]. International Journal of Heat and Mass Transfer, 2014, 71: 593-605. DOI:10.1016/j.ijheatmasstransfer.2013.12.057
-
[21]乔纬韬. 两相流微通道换热特性的仿真与实验研究[D]. 成都: 电子科技大学, 2016.
-
[22]QU W L, MUDAWAR I. Measurement and correlation of critical heat flux in two-phase micro-channel heat sinks[J]. International Journal of Heat and Mass Transfer, 2004, 47(10): 2045-2059.
-
[23]KOSAR A, KUO C J, PELES Y. Suppression of boiling flow oscillations in parallel micro-channels by inlet restrictors[J]. Journal of Heat Transfer, 2006, 128(3): 251-260. DOI:10.1115/1.2150837