|
|
|
发布时间: 2023-10-28 |
综合能源 |
|
|
|
收稿日期: 2023-07-07
基金项目: 国家自然科学基金(52177098)
中图法分类号: TM315
文献标识码: A
文章编号: 2096-8299(2023)05-0415-11
|
摘要
为促进微电网群新能源消纳和低碳经济运行, 在共享经济背景下, 提出了一种基于合作博弈的含共享氢储能(SHES)的微电网群低碳协同优化运行方法, 以兼顾SHES和微电网群的利益。首先, 提出SHES和微电网群的能量交互运行框架; 其次, 分别以SHES运营效益最大和各微电网运营成本最小为目标, 建立了基于合作博弈的电氢能源协同运行模型; 然后, 考虑各主体隐私性, 采用交替方向乘子法(ADMM)算法对模型进行分布式求解; 最后, 进行算例仿真。结果表明, 通过SHES与各微电网的协同运行, 有效改善了各主体的运行情况, 促进新能源就地消纳, 降低了碳排放。
关键词
共享氢储能; 综合能源微电网群; 合作博弈
Abstract
In order to promote the consumption of new energy and the low-carbon economic operation in microgrid cluster, under the background of sharing economy, a low-carbon collaborative optimization operation method of microgrid with shared hydrogen energy storage (SHES) based on cooperative game is proposed to give consideration to the benefits of SHES and microgrid cluster.Firstly, a framework for energy interaction and operation of SHES and microgrid cluster is proposed.Subsequently, with the goals of maximizing the operational benefits of SHES and minimizing the operational costs of each microgrid, a collaborative game based model for the coordinated operation of electric hydrogen energy is established.Then, considering the privacy of each subject, the ADMM algorithm is used to solve the model in a distributed manner.Finally, the numerical simulation shows that the collaborative operation of SHES and various microgrids can effectively improve the operation of various entities, promote the on-site consumption of new energy, and reduce carbon emissions.
Key words
shared hydrogen energy storage; integrated energy microgrid cluster; cooperative game
“双碳”背景下, 能源行业逐步向清洁低碳结构转型。综合能源微电网充分发挥不同能源互补特性, 能够实现能源的梯级利用与合理分配, 对促进新能源消纳和碳减排, 实现我国的“双碳”目标具有重要意义[1-2]。此外, 随着分布式多能市场的兴起与发展, 未来在用能侧将出现大量分属不同利益主体的综合能源微电网, 而相邻综合能源微电网以微电网群的形式协同运行将是综合能源微电网今后发展的重要趋势之一[3-4]。对于配置储能系统的单个综合能源微电网而言, 由于储能单位投资成本较高, 配置容量较小, 故其调度能力十分有限[5-6]。在电制氢技术的不断发展下, 微电网间实现电能和氢能的共享能够进一步促进群内能源的高效互补与就地消纳, 进而提升各微电网的运行经济性。与电能相比, 氢能因其清洁低碳、能量密度高、大规模长周期、运输距离远、生产消纳渠道多元、综合利用效率高等优势, 受到人们的广泛关注[7-9]。利用电解槽、储氢罐和燃料电池协同优化的氢储能系统已被证明是实现电氢协同优化的有效途径。因此, 本文在微电网群中引入共享氢储能(Shared Hydrogen Energy Storage, SHES)以降低微电网的投资建设成本, 实现微电网间的电氢高效共享。然而, SHES与各微电网分属于不同的利益主体, 彼此之间存在复杂利益, 给系统协同运行带来挑战。因此, 合理制定SHES与各微电网之间的协同运行方法, 能有效提升微电网参与能源共享的积极性, 促进分布式新能源的就地消纳。
针对含共享储能的微电网群协同优化问题, 目前多采用博弈论方法进行研究。文献[10]提出基于储能电站服务的多微电网系统双层优化配置方案, 在降低用户成本的同时节约储能资源, 实现多主体互利共赢。文献[11]提出微电网运营商与用户聚合商的主从博弈模型, 引入共享储能, 提高了用户电热调节的灵活性, 提升了用户的收益。文献[12]提出共享储能动态容量配置模型, 并通过算例仿真验证了所提模型能为各微电网分配最优容量, 兼顾多微电网与共享储能的收益。文献[13]提出配有储能系统的智能楼宇运营商的概念, 实现直接和缓冲能量共享, 可提升经济效益, 促进楼宇光伏发电的就地消纳。文献[14]提出以共享储能为主体, 各微电网为从体的一主多从博弈模型, 在提高自身利润的同时, 缓解微电网群并网功率波动。文献[15]提出考虑电热交互和共享储能的多微电网优化运行方法, 算例仿真验证了引入共享储能能够提高微电网运行的经济性。
综上所述, 已有研究存在以下不足: 共享储能多采用电储能形式, 忽视了SHES可实现电氢能源的同时共享; 多采用主从博弈的方法构建共享储能与多微电网的协同优化模型, 在主从博弈框架下各主体均以自身效益最大为目标, 缺乏对整体利益的考虑。因此, 本文提出一种基于SHES的园区综合能源微电网群合作运行方法, 在微电网模型中考虑了燃气掺氢, 以进一步提升各微电网和SHES运行的经济性和低碳性, 实现园区内分布式能源的高效利用。
1 基于合作博弈的SHES与微电网群协同优化运行建模
1.1 SHES运行示意
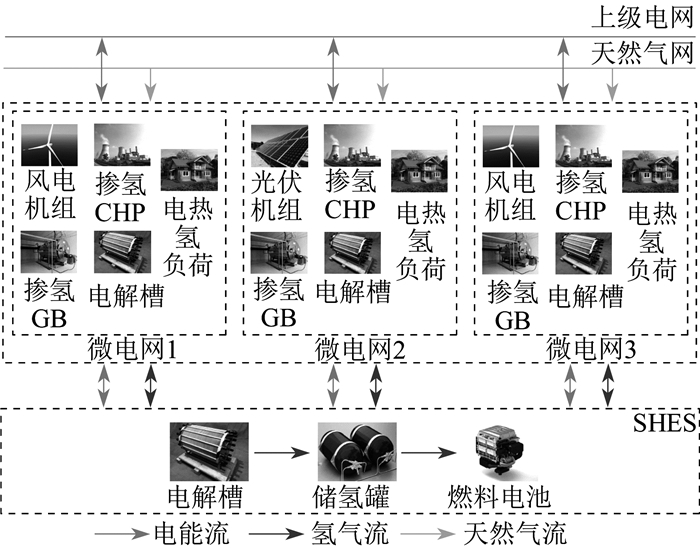
图 1为含SHES的园区综合能源微电网群合作运行示意。其中, 各微电网通过新能源机组、掺氢热电联产机组(Combined Heat and Power, CHP)、掺氢燃气锅炉(Gas Boiler, GB)为自身用户提供电能和热能, 并通过电解槽装置实现电解水制氢。
由图 1可知, 考虑到园区微电网对储能投资建设成本较为敏感, 投资积极性较低; 本文提出的共享氢储能由第三方储能运营商独立投资建设, 并向各微电网提供充放电能和氢能的服务, 各微电网与SHES分属于不同的利益主体。当微电网存在能量富余时, 可将其出售给SHES; 而当微电网存在能量缺额时, 可向SHES购买能量以满足自身用能需求, 微电网之间通过SHES间接实现了能源共享。
1.2 SHES运行模型
1.2.1 目标函数
SHES由3部分组成: 电解槽(Electrolyzer, EL)、储氢罐(Hydrogen Storage Tank, HST)及燃料电池(Fuel Cell, FC)。其运行目标为日运营效益最大化, 为
| $ \max U^{\mathrm{SHES}}=I^{\mathrm{MMG}}-C^{\mathrm{OM}} $ | (1) |
式中: USHES——SHES日运营效益;
IMMG——SHES与微电网群的能源交易收益;
COM——SHES运维成本。
各项费用计算公式为
| $ \left\{\begin{array}{l} I^{\mathrm{MMG}}=\sum\limits_{i=1}^{N} \sum\limits_{t=1}^{T}\left(u_{i, t}^{\mathrm{ele}} P_{i, t}^{\mathrm{sh}}+u_{i, t}^{\mathrm{H}_{2}} V_{i, t}^{\mathrm{sh}}\right) \\ C^{\mathrm{OM}}=\sum\limits_{t=1}^{T}\left[\delta^{\mathrm{EL}} P_{t}^{\mathrm{EL}}+\delta^{\mathrm{FC}} P_{t}^{\mathrm{FC}}+\delta^{\mathrm{HST}}\left(V_{t}^{\mathrm{H}_{2}, \mathrm{ch}}+V_{t}^{\mathrm{H}_{2}, \mathrm{dis}}\right)\right] \end{array}\right. $ | (2) |
式中: N——微电网数;
T——时段数;
ui, tele、ui, tH2——t时刻SHES与微电网i之间的电交易价格和氢交易价格;
Pi, tsh、Vi, tsh——t时刻SHES与微电网i之间的电交易量和氢交易量, 正值时表示SHES向微电网i售能, 负值时表示SHES向微电网i购能;
δEL、δFC、δHST——电解槽、燃料电池、储氢罐的单位运维成本;
PtEL——t时刻电解槽消耗电功率;
PtFC——t时刻燃料电池输出电功率;
VtH2, ch、VtH2, dis——t时刻储氢罐充氢气量和放氢气量。
1.2.2 约束条件
电解槽通过电解水将电能转化为氢气, 其模型为
| $ V_{t}^{\mathrm{H}_{2}, \mathrm{EL}}=\frac{\eta^{\mathrm{EL}} P_{t}^{\mathrm{EL}} \Delta t}{H_{\mathrm{HV}}^{\mathrm{H}_{2}}} $ | (3) |
| $ P_{\min }^{\mathrm{EL}} \leqslant P_{t}^{\mathrm{EL}} \leqslant P_{\max }^{\mathrm{EL}} $ | (4) |
式中: VtH2, EL——t时刻电解槽制氢量;
ηEL——电解槽制氢效率;
Δt——单位调度时段;
HHVH2——氢气热值;
PmaxEL、PminEL——电解槽消耗电功率的上下限。
燃料电池通过氧化还原反应将氢气和氧气中的化学能转化为电能。其模型为
| $ P_{t}^{\mathrm{FC}}=\eta^{\mathrm{FC}} V_{t}^{\mathrm{H}_{2}, \mathrm{FC}} \frac{H_{\mathrm{HV}}^{\mathrm{H}_{2}}}{\Delta t} $ | (5) |
| $ P_{\min }^{\mathrm{FC}} \leqslant P_{t}^{\mathrm{FC}} \leqslant P_{\max }^{\mathrm{FC}} $ | (6) |
式中: ηFC——燃料电池发电效率;
VtH2, FC——燃料电池耗氢量;
PmaxFC、PminFC——燃料电池输出电功率的上下限。
储氢罐为氢能存储的核心设备。其模型为
| $ 0 \leqslant V_{t}^{\mathrm{H}_{2}, \text { ch }} \leqslant U_{t}^{\mathrm{H}_{2}, \text { ch }} V_{\max }^{\mathrm{H}_{2}} $ | (7) |
| $ 0 \leqslant V_{t}^{\mathrm{H}_{2}, \mathrm{dis}} \leqslant U_{t}^{\mathrm{H}_{2}, \text { dis }} V_{\max }^{\mathrm{H}_{2}} $ | (8) |
| $ 0 \leqslant U_{t}^{\mathrm{H}_{2}, \text { ch }}+U_{t}^{\mathrm{H}_{2}, \text { dis }} \leqslant 1 $ | (9) |
| $ V_{t}^{\mathrm{HST}}=V_{t-1}^{\mathrm{HST}}+\left(\eta^{\mathrm{H}_{2}, \text { ch }} V_{t}^{\mathrm{H}_{2}, \text { ch }}-\frac{V_{t}^{\mathrm{H}_{2}, \text { dis }}}{\eta^{\mathrm{H}_{2}, \text { dis }}}\right) $ | (10) |
| $ V_{\min }^{\mathrm{HST}} \leqslant V_{t}^{\mathrm{HST}} \leqslant V_{\max }^{\mathrm{HST}} $ | (11) |
| $ V_{0}^{\mathrm{HST}}=V_{24}^{\mathrm{HST}} $ | (12) |
式中: UtH2, ch、UtH2, dis——t时刻储氢罐充电和放电标识;
VmaxH2——储氢罐充放氢气量上限;
VtHST——t时刻储氢罐的储氢量;
ηH2, ch、ηH2, dis——t时刻储氢罐的充电效率和放电效率;
VmaxHST、VminHST——储氢罐储氢量的上下限;
V0HST、V24HST——调度周期内储氢罐首末时段的储氢量。
SHES需要时刻满足电功率和氢功率平衡约束, 计算公式为
| $ \sum\limits_{i=1}^{N} P_{i, t}^{\mathrm{ele}, \mathrm{s}}=P_{t}^{\mathrm{EL}} $ | (13) |
| $ \sum\limits_{i=1}^{N} P_{i, t}^{\mathrm{ele}, \mathrm{b}}=P_{t}^{\mathrm{FC}} $ | (14) |
| $ \begin{aligned} & \sum\limits_{i=1}^{N} V_{i, t}^{\mathrm{H}_{2}, \mathrm{~s}}+V_{t}^{\mathrm{H}_{2}, \mathrm{EL}}+V_{t}^{\mathrm{H}_{2}, \mathrm{dis}}= \\ & \sum\limits_{i=1}^{N} V_{i, t}^{\mathrm{H}_{2}, \mathrm{~b}}+V_{t}^{\mathrm{H}_{2}, \mathrm{FC}}+V_{t}^{\mathrm{H}_{2}, \mathrm{ch}} \end{aligned} $ | (15) |
式中: Pi, tele, s、Pi, tele, b——t时刻微电网i向SHES的售电量和购电量;
Vi, tH2, s、Vi, tH2, b——t时刻微电网i向SHES的售氢量和购氢量。
此外, SHES与微电网i的能源交易量满足约束条件为
| $ \begin{cases}P_{i, t}^{\mathrm{ele}, \mathrm{s}}=P_{i, t}^{\mathrm{sh}}, & P_{i, t}^{\mathrm{sh}}<0 \\ P_{i, t}^{\mathrm{ele}, \mathrm{b}}=P_{i, t}^{\mathrm{sh}}, & P_{i, t}^{\mathrm{sh}}>0 \\ V_{i, t}^{\mathrm{H}_{2}, \mathrm{~s}}=V_{i, t}^{\mathrm{sh}}, & V_{i, t}^{\mathrm{sh}}<0 \\ V_{i, t}^{\mathrm{H}_{2}, \mathrm{~b}}=V_{i, t}^{\mathrm{sh}}, & V_{i, t}^{\mathrm{sh}}>0\end{cases} $ | (16) |
1.3 综合能源微电网运行模型
1.3.1 目标函数
综合能源微电网的运行目标为日运营成本最小化为
| $ \min U_{i}^{\mathrm{MG}}=C_{i}^{\mathrm{SHES}}+C_{i}^{\mathrm{OM}}+C_{i}^{\mathrm{GRID}}+C_{i}^{\mathrm{CO}_{2}} $ | (17) |
式中: UiMG——微电网i日运营成本;
CiSHES——微电网i与SHES的能源交易成本;
CiOM——微电网i设备运维成本;
CiGRID——微电网i与上级网络的能源交易成本;
CiCO2——微电网i碳排放成本。
各项费用具体计算公式为
| $ \left\{\begin{array}{l} C_{i}^{\mathrm{SHES}}=\sum\limits_{t=1}^{T}\left(u_{i, t}^{\mathrm{ele}} P_{i, t}^{\mathrm{sh}}+u_{i, t}^{\mathrm{H}_{2}} V_{i, t}^{\mathrm{sh}}\right) \\ C_{i}^{\mathrm{OM}}=\sum\limits_{t=1}^{T}\left(\delta^{\mathrm{CHP}} P_{i, t}^{\mathrm{CHP}}+\delta^{\mathrm{GB}} Q_{i, t}^{\mathrm{GB}}+\delta^{\mathrm{MGEL}} P_{i, t}^{\mathrm{MGEL}}\right) \\ C_{i}^{\mathrm{GRID}}=\sum\limits_{t=1}^{T}\left(u_{t}^{\text {grid, } \mathrm{b}} P_{i, t}^{\text {grid, b }}-u_{t}^{\text {grid, s }} P_{i, t}^{\text {grid, s }}+u^{\text {gas }} V_{i, t}^{\text {gas }}\right) \\ C_{i}^{\mathrm{CO}_{2}}=\sum\limits_{t=1}^{T} \lambda^{\mathrm{CO}_{2}}\left(a P_{i, t}^{\text {grid, b }}+b V_{i, t}^{\mathrm{gas}}\right) \end{array}\right. $ | (18) |
式中: δCHP、δGB、δMGEL——热电联产机组、燃气锅炉、电解槽的单位运维成本;
Pi, tCHP——t时刻微电网i热电联产机组输出电功率;
Qi, tGB——t时刻微电网i燃气锅炉输出热功率;
Pi, tMGEL——t时刻微电网i电解槽消耗电功率;
utgrid, b、utgrid, s——t时刻微电网向上级电网的购电和售电价;
ugas——微电网向上级气网的购气价;
Pi, tgrid, b、Pi, tgrid, s——t时刻微电网i向上级电网的购电和售电量;
Vi, tgas——t时刻微电网i向上级气网的购气量;
λCO2——单位碳排放量惩罚系数;
a、b——微电网i向上级电网购电和向上级气网购气的碳排放系数。
1.3.2 约束条件
天然气按一定比例与氢气混合, 供给热电联产机组, 使得燃气的来源更加清洁化。研究表明, 天然气掺氢比在20%以下时, 不会影响燃气轮机的安全运行[16]。燃气轮机在燃烧掺氢燃气生产电能的同时, 产生的高温余热气体经过余热回收装置回收后, 又通过换热器生产热能供用户使用, 其模型为
| $ k_{\mathrm{g} \mathrm{H}_{2}}=\frac{V^{\mathrm{H}_{2}}}{V^{\mathrm{gas}}+V^{\mathrm{H}_{2}}} $ | (19) |
| $ H_{\mathrm{HV}}^{\mathrm{mix}}=k_{\mathrm{gH}_{2}} H_{\mathrm{HV}}^{\mathrm{H}_{2}}+\left(1-k_{\mathrm{gH}_{2}}\right) H_{\mathrm{HV}}^{\mathrm{gas}} $ | (20) |
| $ P_{i, t}^{\mathrm{CHP}}=\eta^{\mathrm{GT}} H_{\mathrm{HV}}^{\mathrm{mix}} \frac{V_{i, t}^{\mathrm{gas}, \mathrm{CHP}}+V_{i, t}^{\mathrm{H}_{2}, \mathrm{CHP}}}{\Delta t} $ | (21) |
| $ Q_{i, t}^{\mathrm{CHP}}=\frac{\left(1-\eta^{\mathrm{GT}}\right) \eta^{\mathrm{WHB}} \eta^{\mathrm{HE}}}{\eta^{\mathrm{GT}}} P_{i, t}^{\mathrm{CHP}} $ | (22) |
| $ P_{\min }^{\mathrm{CHP}} \leqslant P_{i, t}^{\mathrm{CHP}} \leqslant P_{\max }^{\mathrm{CHP}} $ | (23) |
式中: kgH2——天然气掺氢比, 取10%;
VH2、Vgas——掺氢燃气中氢气体积和天然气体积;
HHVmix、HHVgas——掺氢燃气和天然气的热值;
ηGT——燃气轮机发电效率;
Vi, tgas, CHP、Vi, tH2, CHP——燃气轮机消耗的天然气量和氢气量;
Qi, tCHP——t时刻微电网i热电联产机组输出热功率;
ηWHB——余热回收装置的热回收效率;
ηHE——换热器制热效率;
PmaxCHP、PminCHP——热电联产机组电出力上下限。
与掺氢热电联产机组类似, 燃气锅炉燃烧一定掺氢比的掺氢燃气生产热能供用户使用, 不会影响其安全运行, 其模型为
| $ Q_{i, t}^{\mathrm{GB}}=\eta^{\mathrm{GB}} H_{\mathrm{HV}}^{\mathrm{mix}} \frac{V_{i, t}^{\mathrm{gas}, \mathrm{GB}}+V_{i, t}^{\mathrm{H}_{2}, \mathrm{~GB}}}{\Delta t} $ | (24) |
| $ Q_{\min }^{\mathrm{GB}} \leqslant Q_{i, t}^{\mathrm{GB}} \leqslant Q_{\max }^{\mathrm{GB}} $ | (25) |
式中: ηGB——燃气锅炉产热效率;
Vi, tgas, GB、Vi, tH2, GB——燃气锅炉消耗的天然气量和氢气量;
QmaxGB、QminGB——燃气锅炉热出力上下限。
与SHES电解槽类似, 微电网电解槽模型为
| $ V_{i, t}^{\mathrm{H}_{2}, \mathrm{MGEL}}=\frac{\eta^{\mathrm{EL}} P_{i, t}^{\mathrm{MGEL}} \Delta t}{H_{\mathrm{HV}}^{\mathrm{H}_{2}}} $ | (26) |
| $ P_{\min }^{\mathrm{MGEL}} \leqslant P_{i, t}^{\mathrm{MGEL}} \leqslant P_{\max }^{\mathrm{MGEL}} $ | (27) |
式中: Vi, tH2, MGEL——t时刻微电网i电解槽的制氢量;
PmaxMGEL、PminMGEL——微电网i电解槽消耗电功率的上下限。
受输电线路传输容量的限制, 微电网i向上级电网购售电时需满足的约束条件为
| $ 0 \leqslant P_{i, t}^{\text {grid, } \mathrm{b}} \leqslant U_{i, t}^{\text {grid, } \mathrm{b}} P_{\max }^{\text {grid }} $ | (28) |
| $ 0 \leqslant P_{i, t}^{\text {grid, } \mathrm{s}} \leqslant U_{i, t}^{\text {grid, s }} P_{\max }^{\text {grid }} $ | (29) |
| $ 0 \leqslant U_{i, t}^{\text {grid, } \mathrm{b}}+U_{i, t}^{\text {grid, } \mathrm{s}} \leqslant 1 $ | (30) |
式中: Ui, tgrid, b、Ui, tgrid, s——t时刻微电网i向上级电网购售电标识;
Pmaxgrid——微电网i向上级电网单次购电量上限。
微电网i向SHES购售电能和氢能时需要满足的约束为
| $ -P_{\max }^{\mathrm{sh}} \leqslant P_{i, t}^{\mathrm{sh}} \leqslant P_{\max }^{\mathrm{sh}} $ | (31) |
| $ -V_{\max }^{\mathrm{sh}} \leqslant V_{i, t}^{\mathrm{sh}} \leqslant V_{\max }^{\mathrm{sh}} $ | (32) |
式中: Pmaxsh、Vmaxsh——微电网i向SHES单次购售电量和氢量的上限。
为促进各微电网优先考虑与SHES交易, 避免各微电网过多依赖与上级网络交易来维持自身能量平衡, 微电网i与SHES之间的电能、氢能交易价格应满足的约束为
| $ u_{t}^{\text {grid, } \mathrm{s}} \leqslant u_{i, t}^{\text {ele }} \leqslant u_{t}^{\text {grid, } \mathrm{b}} $ | (33) |
| $ u_{\min }^{\mathrm{H}_{2}} \leqslant u_{i, t}^{\mathrm{H}_{2}} \leqslant u_{\max }^{\mathrm{H}_{2}} $ | (34) |
式中: umaxH2、uminH2——微电网i与SHES的氢气交易价格的上下限, 分别取3.5元/m3、1.5元/m3。
微电网i需时刻满足电、热、氢、气的功率平衡约束为
| $ \begin{array}{*{20}{c}} {P_{i, t}^{\mathrm{WT}}+P_{i, t}^{\mathrm{PV}}+P_{i, t}^{\mathrm{CHP}}+P_{i, t}^{\text {grid, } \mathrm{b}}+P_{i, t}^{\mathrm{sh}}= }\\ {P_{i, t}^{\mathrm{ele}, \mathrm{L}}+P_{i, t}^{\mathrm{MGEL}}+P_{i, t}^{\text {grid, } \mathrm{s}} } \end{array} $ | (35) |
| $ Q_{i, t}^{\mathrm{CHP}}+Q_{i, t}^{\mathrm{GB}}=Q_{i, t}^{\mathrm{heat}, \mathrm{L}} $ | (36) |
| $ V_{i, t}^{\mathrm{H}_{2}, \mathrm{MGEL}}+V_{i, t}^{\mathrm{sh}}=V_{i, t}^{\mathrm{H}_{2}, \mathrm{~L}}+V_{i, t}^{\mathrm{H}_{2}, \mathrm{CHP}}+V_{i, t}^{\mathrm{H}_{2}, \mathrm{~GB}} $ | (37) |
| $ V_{i, t}^{\mathrm{gas}}=V_{i, t}^{\mathrm{gas}, \mathrm{CHP}}+V_{i, t}^{\mathrm{gas}, \mathrm{GB}} $ | (38) |
式中: Pi, tWT、Pi, tPV——t时刻微电网i风机输出功率和光伏输出功率;
Pi, tele, L、Qi, theat, L、Vi, tH2, L——t时刻微电网i的电负荷、热负荷和氢负荷。
1.4 SHES和微电网群协同运行模型
SHES与各微电网作为独立且理性的利益主体, 在参与合作博弈时需要保证自身利益不受损害。对此, SHES与各微电网通过议价谈判的方式达成协议, 从而确定SHES与各微电网的能源交易情况, 实现整体利益最大化的同时兼顾各参与者自身的利益诉求。基于纳什谈判的SHES与各微电网之间的合作运行模型为
| $ \left\{\begin{array}{l} \max \left(U^{\mathrm{SHES}}-U_{0}^{\mathrm{SHES}}\right) \prod\limits_{i \in N}\left(U_{i, 0}^{\mathrm{MG}}-U_{i}^{\mathrm{MG}}\right) \\ \text { s. t. } U^{\mathrm{SHES}} \geqslant U_{0}^{\mathrm{SHES}} \\ U_{i, 0}^{\mathrm{MG}} \geqslant U_{i}^{\mathrm{MG}} \\ { 式(2)\sim式(16)、式(18)\sim式(38)} \end{array}\right. $ | (39) |
式中: U0SHES、Ui, 0MG——参与合作前共享氢储能的最优效益和微电网i的最优成本。
式(39)包含能源价格和能源数量的乘积, 属于非凸非线性的优化问题, 难以直接求解, 因此需要将其转换为两个子问题来依次求解。其中: 问题P1为社会效益最大化问题; 问题P2为能源交易支付谈判问题。上标带“*”的变量为问题P1求得的最优解。具体转换过程见文献[17], 本文不再赘述。
社会效益最大化问题P1为
| $ \left\{\begin{aligned} \max [ & \left.\left(-C^{\mathrm{OM}}\right)+\sum\limits_{i=1}^{N}\left(-C_{i}^{\mathrm{OM}}-C_{i}^{\mathrm{GRID}}-C_{i}^{\mathrm{CO}_{2}}\right)\right] \\ \text { s.t. } & { 式(2)\sim式(16)、式(18)\sim式(32)、} \\ & {式(35)\sim式(38)} \end{aligned}\right. $ | (40) |
共享氢储能与各微电网能源交易支付谈判问题P2为
| $ \left\{\begin{array}{l} \max \left[\ln \left(I^{\mathrm{MMG}}-C^{\mathrm{OM} *}-U_{0}^{\mathrm{SHES}}\right)+\right. \\ \left.\sum\limits_{i=1}^{N} \ln \left(U_{i, 0}^{\mathrm{MG}}-C_{i}^{\mathrm{SHES}}-C_{i}^{\mathrm{OM} *}-C_{i}^{\mathrm{GRID} *}-C_{i}^{\mathrm{CO}_{2} *}\right)\right] \\ \text { s. t. } I^{\mathrm{MMG}}-C^{\mathrm{OM} *} \geqslant U_{0}^{\mathrm{SHES}} \\ U_{i, 0}^{\mathrm{MG}} \geqslant C_{i}^{\mathrm{SHES}}+C_{i}^{\mathrm{OM} *}+C_{i}^{\mathrm{GRID} *}+C_{i}^{\mathrm{CO}_{2} *} \\ \text {式(33)}\sim \text {式}(34) \end{array}\right. $ | (41) |
2 模型求解策略
2.1 基于ADMM的社会效益最大化问题P1求解
交替方向乘子法(Alternating Direction Multiplier Method, ADMM)在求解大规模变量优化问题时具有良好的收敛性和较快的求解速度, 同时可以充分保护各参与主体的信息隐私, 故本文采用ADMM对问题P1和P2进行分布式求解。
式(40)中包含了能源交易量的耦合变量, 由于交易双方所期望的能源交易量需保持相等, 故引入以下辅助变量对模型进行解耦:
| $ \left\{\begin{array}{l} P_{i, t}^{\mathrm{sh}, \mathrm{S}}=P_{i, t}^{\mathrm{sh}, \mathrm{G}} \\ V_{i, t}^{\mathrm{sh}, \mathrm{S}}=V_{i, t}^{\mathrm{sh}, \mathrm{G}} \end{array}\right. $ | (42) |
式中: Pi, tsh, S、Vi, tsh, S——SHES期望与微电网i交易的电功率和氢气量;
Pi, tsh, G、Vi, tsh, G——微电网i期望与SHES交易的电功率和氢气量。
对式(40)中的目标函数取相反数, 转化为求解最小值问题, 依据ADMM得到问题P1中各主体的分布式优化模型。
SHES和微电网i的分布式优化模型分别为
| $ \left\{\begin{array}{l} \min L_{P 1}^{\mathrm{SEHES}}=C^{\mathrm{OM}}+ \\ \sum\limits_{i=1}^{N} \sum\limits_{t=1}^{T}\left[\varphi_{i, t}^{\mathrm{e}, \mathrm{S}}\left(P_{i, t}^{\mathrm{sh}, \mathrm{S}}-P_{i, t}^{\mathrm{sh}, \mathrm{G}}\right)+\varphi_{i, t}^{\mathrm{H}_{2}, \mathrm{S}}\left(V_{i, t}^{\mathrm{sh}, \mathrm{S}}-V_{i, t}^{\mathrm{sh}, \mathrm{G}}\right)+\right. \\ \left.\quad \frac{\rho_{1}}{2}\left\|P_{i, t}^{\mathrm{sh}, \mathrm{S}}-P_{i, t}^{\mathrm{sh}, \mathrm{G}}\right\|_{2}^{2}+\frac{\rho_{1}}{2}\left\|V_{i, t}^{\mathrm{sh}, \mathrm{S}}-V_{i, t}^{\mathrm{sh}, \mathrm{G}}\right\|_{2}^{2}\right] \\ \text { s. t. 式(2)} \sim \text {式(16) } \end{array}\right. $ | (43) |
| $ \left\{\begin{array}{l} \min L_{i, P 1}^{\mathrm{MG}}=\left(C_{i}^{\mathrm{OM}}+C_{i}^{\mathrm{GRID}}+C_{i}^{\mathrm{CO}_{2}}\right)+ \\ \sum\limits_{t=1}^{T}\left[\varphi_{i, t}^{\mathrm{e}, \mathrm{G}}\left(P_{i, t}^{\mathrm{sh}, \mathrm{G}}-P_{i, t}^{\mathrm{sh}, \mathrm{S}}\right)+\varphi_{i, t}^{\mathrm{H}_{2}, \mathrm{G}}\left(V_{i, t}^{\mathrm{sh}, \mathrm{G}}-V_{i, t}^{\mathrm{sh}, \mathrm{S}}\right)+\right. \\ \left.\quad \frac{\rho_{1}}{2}\left\|P_{i, t}^{\mathrm{sh}, \mathrm{G}}-P_{i, t}^{\mathrm{sh}, \mathrm{S}}\right\|_{2}^{2}+\frac{\rho_{1}}{2}\left\|V_{i, t}^{\mathrm{sh}, \mathrm{G}}-V_{i, t}^{\mathrm{sh}, \mathrm{S}}\right\|_{2}^{2}\right] \\ \text { s.t. 式(18)} \sim \text {式(32)、式 }(35) \sim \text {式}(38) \end{array}\right. $ | (44) |
式中: LP1SHES、Li, P1MG——问题P1下SHES和微电网i的增广拉格朗日函数;
φi, te, S、φi, te, G——问题P1下SHES和微电网i的电拉格朗日乘子;
φi, tH2, S、φi, tH2, G——问题P1下SHES和微电网i的氢拉格朗日乘子;
ρ1——问题P1的惩罚因子。
用上标k代表k次迭代后的相关变量, 则(k+1)次迭代后SHES变量更新公式为
| $ \left(\begin{array}{l} P_{i, t}^{\mathrm{sh}, \mathrm{S}, k+1} \\ V_{i, t}^{\mathrm{sh}, \mathrm{S}, k+1} \end{array}\right)=\arg \min L_{P 1}^{\mathrm{SHES}}\left(\begin{array}{l} P_{i, t}^{\mathrm{sh}, \mathrm{S}, k}, P_{i, t}^{\mathrm{sh}, \mathrm{G}, k}, \varphi_{i, t}^{\mathrm{e}, \mathrm{S}, k} \\ V_{i, t}^{\mathrm{sh}, \mathrm{S}, k}, V_{i, t}^{\mathrm{sh}, \mathrm{G}, k}, \varphi_{i, t}^{\mathrm{H}_{2}, \mathrm{~S}, k} \end{array}\right) $ | (45) |
微电网i变量更新公式为
| $ \left(\begin{array}{c} P_{i, t}^{\mathrm{sh}, \mathrm{G}, k+1} \\ V_{i, t}^{\mathrm{sh}, \mathrm{G}, k+1} \end{array}\right)=\arg \min L_{i, P 1}^{\mathrm{MG}}\left(\begin{array}{l} P_{i, t}^{\mathrm{sh}, \mathrm{G}, k}, P_{i, t}^{\mathrm{sh}, \mathrm{S}, k+1}, \varphi_{i, t}^{\mathrm{e}, \mathrm{G}, k} \\ V_{i, t}^{\mathrm{sh}, \mathrm{G}, k}, V_{i, t}^{\mathrm{sh}, \mathrm{S}, k+1}, \varphi_{i, t}^{\mathrm{H}_{2}, \mathrm{G}, k} \end{array}\right) $ | (46) |
拉格朗日乘子更新公式为
| $ \left\{\begin{array}{l} \varphi_{i, t}^{\mathrm{e}, \mathrm{S}, k+1}=\varphi_{i, t}^{\mathrm{e}, \mathrm{S}, k}+\rho_{1}\left(P_{i, t}^{\mathrm{sh}, \mathrm{S}, k+1}-P_{i, t}^{\mathrm{sh}, \mathrm{G}, k+1}\right) \\ \varphi_{i, t}^{\mathrm{H}_{2}, \mathrm{~S}, k+1}=\varphi_{i, t}^{\mathrm{H}_{2}, \mathrm{~S}, k}+\rho_{1}\left(V_{i, t}^{\mathrm{sh}, \mathrm{S}, k+1}-V_{i, t}^{\mathrm{sh}, \mathrm{G}, k+1}\right) \\ \varphi_{i, t}^{\mathrm{e}, \mathrm{G}, k+1}=\varphi_{i, t}^{\mathrm{e}, \mathrm{G}, k}+\rho_{1}\left(P_{i, t}^{\mathrm{sh}, \mathrm{G}, k+1}-P_{i, t}^{\mathrm{sh}, \mathrm{S}, k+1}\right) \\ \varphi_{i, t}^{\mathrm{H}_{2}, \mathrm{G}, k+1}=\varphi_{i, t}^{\mathrm{H}_{2}, \mathrm{G}, k}+\rho_{1}\left(V_{i, t}^{\mathrm{sh}, \mathrm{G}, k+1}-V_{i, t}^{\mathrm{sh}, \mathrm{S}, k+1}\right) \end{array}\right. $ | (47) |
收敛条件为原始残差和对偶残差小于收敛阈值。公式为
| $ \left\{\begin{array}{l} r_{1}^{\mathrm{e}, k}=\sum\limits_{i=1}^{N} \sum\limits_{t=1}^{T}\left\|P_{i, t}^{\mathrm{sh}, \mathrm{S}, k}-P_{i, t}^{\mathrm{sh}, \mathrm{G}, k}\right\|_{2}^{2} \leqslant \varepsilon_{1} \\ r_{1}^{\mathrm{H}_{2}, k}=\sum\limits_{i=1}^{N} \sum\limits_{t=1}^{T}\left\|V_{i, t}^{\mathrm{sh}, \mathrm{S}, k}-V_{i, t}^{\mathrm{sh}, \mathrm{G}, k}\right\|_{2}^{2} \leqslant \varepsilon_{1} \\ s_{1}^{\mathrm{e}, k}=\sum\limits_{i=1}^{N} \sum\limits_{t=1}^{T}\left\|P_{i, t}^{\mathrm{sh}, \mathrm{S}, k+1}-P_{i, t}^{\mathrm{sh}, \mathrm{S}, k}\right\|_{2}^{2} \leqslant \varepsilon_{1} \\ s_{1}^{\mathrm{H}_{2}, k}=\sum\limits_{i=1}^{N} \sum\limits_{t=1}^{T}\left\|V_{i, t}^{\mathrm{sh}, \mathrm{S}, k+1}-V_{i, t}^{\mathrm{sh}, \mathrm{S}, k}\right\|_{2}^{2} \leqslant \varepsilon_{1} \end{array}\right. $ | (48) |
式中: r1e, k、r1H2, k——问题P1下电能、氢能的原始残差;
s1e, k、s1H2, k——问题P1下电能、氢能的对偶残差;
ε1——问题P1下的收敛阈值。
2.2 基于ADMM的能源交易支付谈判问题P2求解
式(41)中包含了能源交易量的耦合变量。由于交易双方所期望的能源交易价格同样需保持相等, 故引入辅助变量对模型进行解耦, 为
| $ \left\{\begin{array}{l} u_{i, t}^{\mathrm{ele}, \mathrm{S}}=u_{i, t}^{\mathrm{ele}, \mathrm{G}} \\ u_{i, t}^{\mathrm{H}_{2}, \mathrm{~S}}=u_{i, t}^{\mathrm{H}_{2}, \mathrm{G}} \end{array}\right. $ | (49) |
式中: ui, tele, S、ui, tH2, S——SHES期望与微电网i交易的电能价格和氢气价格;
ui, tele, G、ui, tH2, G——微电网i期望与SHES交易的电能价格和氢气价格。
对式(41)中的目标函数取相反数, 转化为求解最小值问题, 依据ADMM得到问题P2中各主体的分布式优化模型。
SHES的分布式优化模型为
| $ \left\{\begin{array}{l} \min L_{P 2}^{\mathrm{SHES}}=-\ln \left[\sum\limits_{i=1}^{N} \sum\limits_{t=1}^{T}\left(u_{i, t}^{\mathrm{ele}, \mathrm{S}} P_{i, t}^{\mathrm{sh} *}+u_{i, t}^{\mathrm{H}_{2}, \mathrm{~S}} V_{i, t}^{\mathrm{sh} *}\right)-\right. \\ \left.C^{\mathrm{OM} *}-U_{0}^{\mathrm{SHES}}\right]+\sum\limits_{i=1}^{N} \sum\limits_{t=1}^{T}\left[\mu_{i, t}^{\mathrm{e}, \mathrm{S}}\left(u_{i, t}^{\mathrm{ele}, \mathrm{S}}-u_{i, t}^{\mathrm{ele}, \mathrm{G}}\right)+\right. \\ \quad \mu_{i, t}^{\mathrm{H}_{2}, \mathrm{~S}}\left(u_{i, t}^{\mathrm{H}_{2}, \mathrm{~S}}-u_{i, t}^{\mathrm{H}_{2}, \mathrm{G}}\right)+ \\ \left.\quad \frac{\rho_{2}}{2}\left\|u_{i, t}^{\mathrm{ele}, \mathrm{S}}-u_{i, t}^{\mathrm{ele}, \mathrm{G}}\right\|_{2}^{2}+\frac{\rho_{2}}{2}\left\|u_{i, t}^{\mathrm{H}_{2}, \mathrm{~S}}-u_{i, t}^{\mathrm{H}_{2}, \mathrm{G}}\right\|_{2}^{2}\right] \\ \text { s. t. } I^{\mathrm{MMG}}-C^{\mathrm{OM} *} \geqslant U_{0}^{\mathrm{SHES}} \\ \text {式(33)} \sim \text {式}(34) \end{array}\right. $ | (50) |
微电网i的分布式优化模型为
| $ \left\{\begin{array}{l} \min L_{i, P 2}^{\mathrm{MG}}=-\ln \left[U_{i, 0}^{\mathrm{MG}} V-\sum\limits_{t=1}^{T}\left(u_{i, t}^{\mathrm{ele}, \mathrm{G}} P_{i, t}^{\mathrm{sh} *}+u_{i, t}^{\mathrm{H}_{2}, \mathrm{G}} V_{i, t}^{\mathrm{sh} *}\right)-\right. \\ \left.\quad C_{i}^{\mathrm{OM} *}-C_{i}^{\mathrm{GRID} *}-C_{i}^{\mathrm{CO}_{2} *}\right]+ \\ \quad \sum\limits_{t=1}^{T}\left[\mu_{i, t}^{\mathrm{e}, \mathrm{G}}\left(u_{i, t}^{\mathrm{ele}, \mathrm{G}}-u_{i, t}^{\mathrm{ele}, \mathrm{S}}\right)+\mu_{i, t}^{\mathrm{H}_{2}, \mathrm{G}}\left(u_{i, t}^{\mathrm{H}_{2}, \mathrm{G}}-u_{i, t}^{\mathrm{H}_{2}, \mathrm{~S}}\right)+\right. \\ \left.\quad \frac{\rho_{2}}{2}\left\|u_{i, t}^{\mathrm{ele}, \mathrm{G}}-u_{i, t}^{\mathrm{ele}, \mathrm{S}}\right\|_{2}^{2}+\frac{\rho_{2}}{2}\left\|u_{i, t}^{\mathrm{H}_{2}, \mathrm{~S}}-u_{i, t}^{\mathrm{H}_{2}, \mathrm{G}}\right\|_{2}^{2}\right] \\ \text { s. t. } U_{i, 0}^{\mathrm{MG}} \geqslant C_{i}^{\mathrm{SHES}}+C_{i}^{\mathrm{OM} *}+C_{i}^{\mathrm{GRID} *}+C_{i}^{\mathrm{CO}_{2} *} \\ \text { 式(33)} \sim \text {式(34) } \end{array}\right. $ | (51) |
式中: LP2SHES、Li, P2MG——问题P2下SHES和微电网i的增广拉格朗日函数;
μi, te, S、μi, te, G——问题P2下SHES和微电网i的电拉格朗日乘子;
μi, tH2, S、μi, tH2, G——问题P2下SHES和微电网i的氢拉格朗日乘子;
ρ2——问题P2的惩罚因子。
SHES变量更新公式为
| $ \left(\begin{array}{l}u_{i, t}^{\mathrm{ele}, \mathrm{S}, k+1} \\ u_{i, t}^{\mathrm{H}_{2}, \mathrm{~S}, k+1}\end{array}\right)=\arg \min L_{P 2}^{\mathrm{SHES}}\left(\begin{array}{l}u_{i, t}^{\mathrm{ele}, \mathrm{S}, k}, u_{i, t}^{\mathrm{ele}, \mathrm{G}, k}, \mu_{i, t}^{\mathrm{e}, \mathrm{S}, k} \\ u_{i, t}^{\mathrm{H}_{2}, \mathrm{~S}, k}, u_{i, t}^{\mathrm{H}_{2}, \mathrm{G}, k}, \mu_{i, t}^{\mathrm{H}_{2}, \mathrm{~S}, k}\end{array}\right) $ | (52) |
微电网i变量更新公式为
| $ \left(\begin{array}{c}u_{i, t}^{\mathrm{ele}, \mathrm{G}, k+1} \\ u_{i, t}^{\mathrm{H}_{2}, \mathrm{G}, k+1}\end{array}\right)=\arg \min L_{i, P 2}^{\mathrm{MG}}\left(\begin{array}{l}u_{i, t}^{\mathrm{ele}, \mathrm{G}, k}, u_{i, t}^{\mathrm{ele}, \mathrm{S}, k+1}, \mu_{i, t}^{\mathrm{e}, \mathrm{G}, k} \\ u_{i, t}^{\mathrm{H}_{2}, \mathrm{G}, k}, u_{i, t}^{\mathrm{H}_{2}, \mathrm{~S}, k+1}, \mu_{i, t}^{\mathrm{H}_{2}, \mathrm{G}, k}\end{array}\right) $ | (53) |
拉格朗日乘子更新公式为
| $ \left\{\begin{array}{l} \mu_{i, t}^{\mathrm{e}, \mathrm{S}, k+1}=\mu_{i, t}^{\mathrm{e}, \mathrm{S}, k}+\rho_{2}\left(u_{i, t}^{\mathrm{ele}, \mathrm{S}, k+1}-u_{i, t}^{\mathrm{ele}, \mathrm{G}, k+1}\right) \\ \mu_{i, t}^{\mathrm{H}_{2}, \mathrm{~S}, k+1}=\mu_{i, t}^{\mathrm{H}_{2}, \mathrm{~S}, k}+\rho_{2}\left(u_{i, t}^{\mathrm{H}_{2}, \mathrm{~S}, k+1}-u_{i, t}^{\mathrm{H}_{2}, \mathrm{G}, k+1}\right) \\ \mu_{i, t}^{\mathrm{e}, \mathrm{G}, k+1}=\mu_{i, t}^{\mathrm{e}, \mathrm{G}, k}+\rho_{2}\left(u_{i, t}^{\mathrm{ele}, \mathrm{G}, k+1}-u_{i, t}^{\mathrm{ele}, \mathrm{S}, k+1}\right) \\ \mu_{i, t}^{\mathrm{H}_{2}, \mathrm{G}, k+1}=\mu_{i, t}^{\mathrm{H}_{2}, \mathrm{G}, k}+\rho_{2}\left(u_{i, t}^{\mathrm{H}_{2}, \mathrm{G}, k+1}-u_{i, t}^{\mathrm{H}_{2}, \mathrm{~S}, k+1}\right) \end{array}\right. $ | (54) |
收敛条件为原始残差和对偶残差小于收敛阈值。公式为
| $ \left\{\begin{array}{l} r_{2}^{\mathrm{e}, k}=\sum\limits_{i=1}^{N} \sum\limits_{t=1}^{T}\left\|u_{i, t}^{\mathrm{ele}, \mathrm{S}, k}-u_{i, t}^{\mathrm{ele}, \mathrm{G}, k}\right\|_{2}^{2} \leqslant \varepsilon_{2} \\ r_{2}^{\mathrm{H}_{2}, k}=\sum\limits_{i=1}^{N} \sum\limits_{t=1}^{T}\left\|u_{i, t}^{\mathrm{H}_{2}, \mathrm{~S}, k}-u_{i, t}^{\mathrm{H}_{2}, \mathrm{G}, k}\right\|_{2}^{2} \leqslant \varepsilon_{2} \\ s_{2}^{\mathrm{e}, k}=\sum\limits_{i=1}^{N} \sum\limits_{t=1}^{T}\left\|u_{i, t}^{\mathrm{ele}, \mathrm{S}, k+1}-u_{i, t}^{\mathrm{ele}, \mathrm{S}, k}\right\|_{2}^{2} \leqslant \varepsilon_{2} \\ S_{2}^{\mathrm{H}_{2}, k}=\sum\limits_{i=1}^{N} \sum\limits_{t=1}^{T}\left\|u_{i, t}^{\mathrm{H}_{2}, \mathrm{~S}, k+1}-u_{i, t}^{\mathrm{H}_{2}, \mathrm{~S}, k}\right\|_{2}^{2} \leqslant \varepsilon_{2} \end{array}\right. $ | (55) |
式中: r2e, k、r2H2, k——问题P2下电能、氢能的原始残差;
s2e, k、s2H2, k——问题P2下电能、氢能的对偶残差;
ε2——问题P2下的收敛阈值。
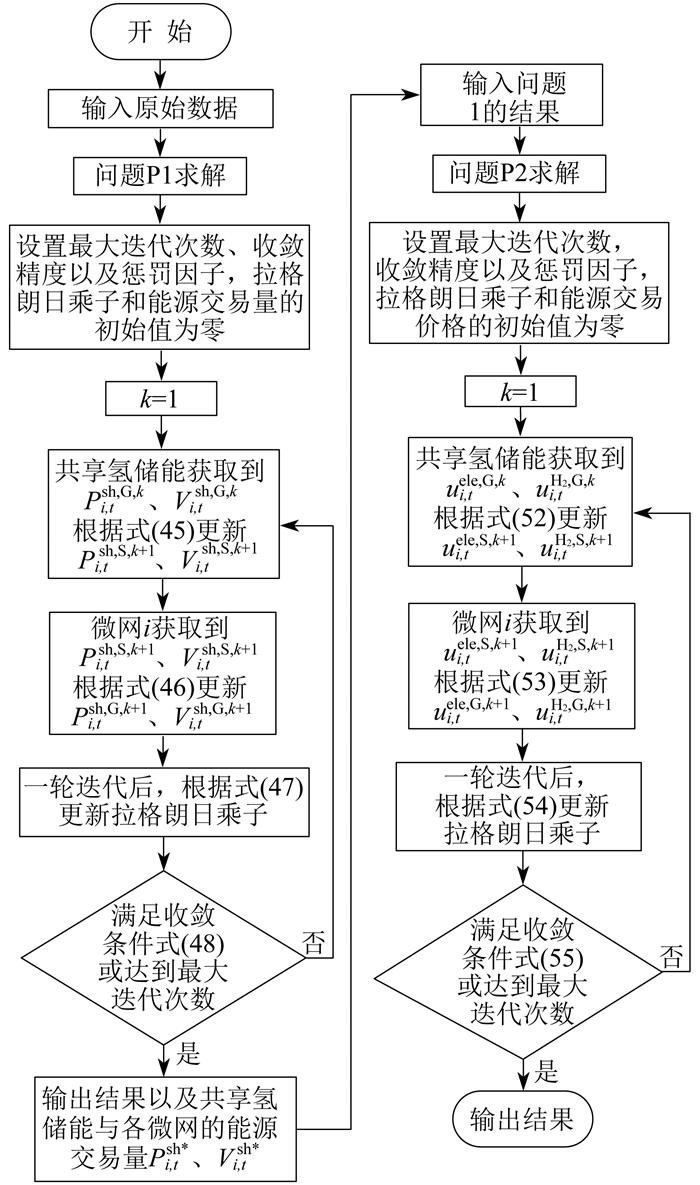
关于问题P1和问题P2中分布式优化模型的具体求解流程如图 2所示。
3 算例验证
3.1 测试系统参数
分别以MG1、MG2、MG3指代微电网1、微电网2、微电网3。其中, MG1和MG3各配备1台风电机组, MG2配备1台光伏机组。除新能源机组外, 各微电网还配有相同参数的热电联产机组、燃气锅炉和电解槽。微电网运行参数如表 1所示。SHES运行参数如表 2所示。
表 1
微电网运行参数
| 参数 | 数值 | 参数 | 数值 | |
| HHVgas/(kWh·m-3) | 9.75 | ηGB | 0.85 | |
| HHVH2/(kWh·m-3) | 3.55 | QmaxGB/kW | 300 | |
| kgH2 | 0.1 | QminGB/kW | 50 | |
| ηGT | 0.4 | ηEL | 0.88 | |
| ηWHB | 0.83 | PmaxMGEL/kW | 150 | |
| ηHE | 0.9 | Pmaxgrid/kW | 1 000 | |
| PmaxCHP/kW | 500 | Pmaxsh/kW | 500 | |
| PminCHP/kW | 50 | Vmaxsh/m3 | 10 |
表 2
SHES运行参数
| 参数 | 数值 | 参数 | 数值 | |
| PmaxEL | 1 500 | VmaxH2, dis | 150 | |
| PmaxFC | 1 500 | ηH2, ch | 0.95 | |
| ηEL | 0.88 | ηH2, dis | 0.95 | |
| ηFC | 0.95 | VmaxHST | 450 | |
| VmaxH2, ch | 150 | VminHST | 50 |
上级网络能源价格如表 3所示。其中,在00:00—24:00, 天然气价格为3元/m3。碳排放参数如表 4所示。
表 3
上级网络能源价格
| 类别 | 时段 | 价格/(元·kWh-1) |
| 上网电价 | 00:00—08:00 | 0.40 |
| 12:00—16:00, 22:00—24:00 | 0.70 | |
| 08:00—12:00, 16:00—22:00 | 1.10 | |
| 回购电价 | 00:00—24:00 | 0.25 |
表 4
碳排放参数
| 参数 | 数值 |
| a/(kg·kW-1) | 0.889 |
| b/(kg·kW-1) | 0.725 |
| λCO2/(元·kg-1) | 0.252 |
3.2 优化结果分析
3.2.1 微电网群运行结果分析
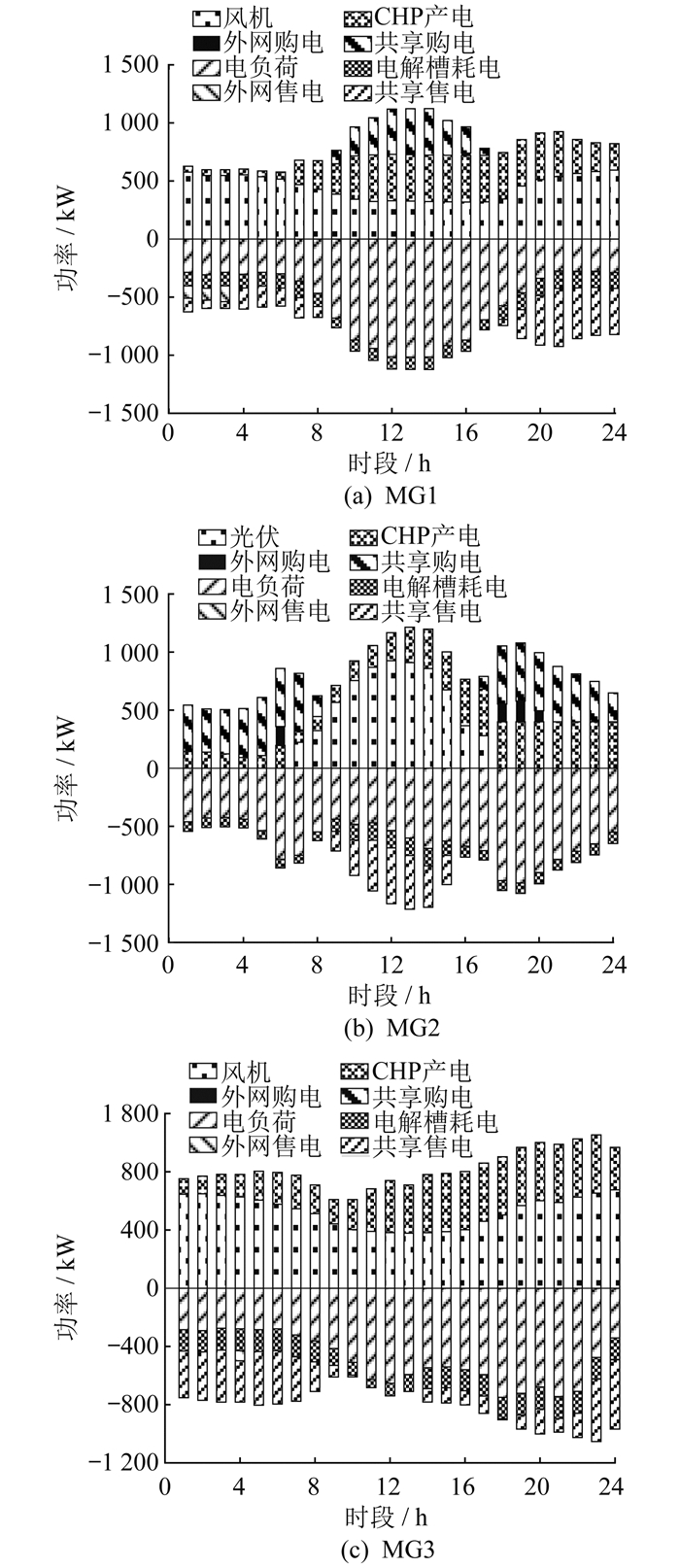
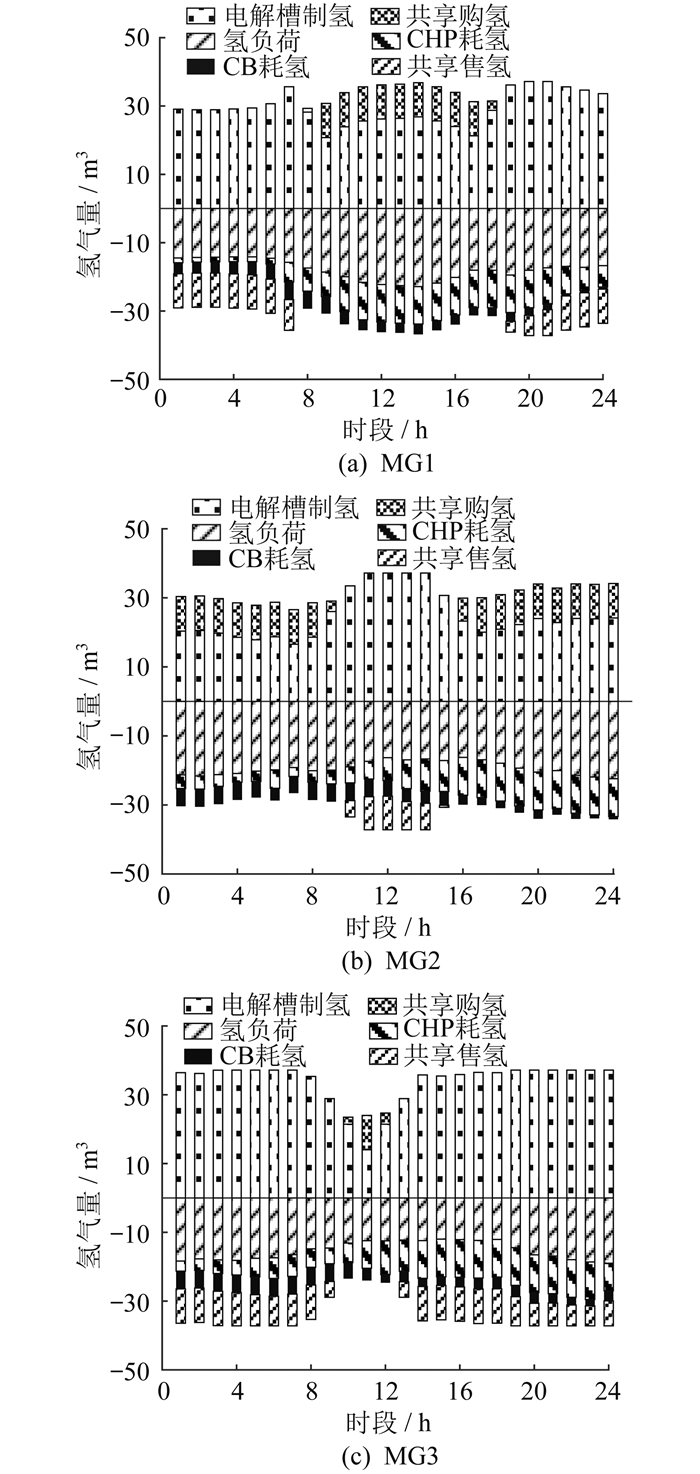
合作运行下MG1、MG2和MG3的电能、氢能优化运行结果如图 3和图 4所示。
由图 3和图 4可知, 各MG主要通过新能源机组和CHP机组给电负荷和电解槽供电, 多余或不足的部分通过与SHES或上级电网电能交易平衡。在00:00—08:00和18:00—24:00时段, MG1电负荷处于较低水平, MG2电负荷处于较高水平。MG1自身风电资源较为富足, 供电压力较小, 故MG1选择在此时段将多余的电能一部分用于电解槽制氢, 一部分出售给SHES, 只有少量的电能出售给上级电网。MG2由于光伏机组在该时段不出力, 故只能选择从SHES和上级电网购电来缓解供电压力。在09:00—15:00时段, 情况则相反, MG1电负荷处于较高水平, MG2电负荷处于较低水平, 此时MG1增大CHP机组出力, 同时向SHES购买电能来满足用电需求, 而MG2则有充裕的电能可对外出售。对于MG3, 在所有时段, 其风电机组和CHP机组出力完全能够满足自身用电需求, 多余的电能首先被用于电解槽制氢, 其余的几乎全被出售给SHES, 以供其他MG购买使用。
关于氢能优化情况, 可以看到各MG主要通过电解槽制氢来给氢负荷和掺氢燃气机组提供所需的氢气, 多余或不足的部分则通过与SHES进行氢气交易来平衡。对于MG1, 在00:00—08:00和20:00—24:00时段, 由于其风电机组出力较高, 故MG1有充足的电能提供给电解槽制氢, 满足自身需求的同时还能对外出售一部分氢气; 在08:00—18:00时段, 其风电出力较低, 而氢负荷以及燃气机组所需的氢气量却相对较高, 故MG1选择向SHES购买氢气来满足用氢需求。对于MG2, 仅在10:00—14:00时段, 光伏发电量处于较高水平, 此时MG2有富余的电能用于制氢并对外出售, 而在其余时段, 电解槽制取的氢气量均无法满足用氢需求, 只能向SHES购买才能维持氢能平衡。对于MG3, 由于其风电资源较为富足, 在大多数时段内, 其电解槽制得的氢气量均能够满足自身需求, 还能够向SHES出售氢气以供其他MG购买使用。
3.2.2 SHES运行结果分析
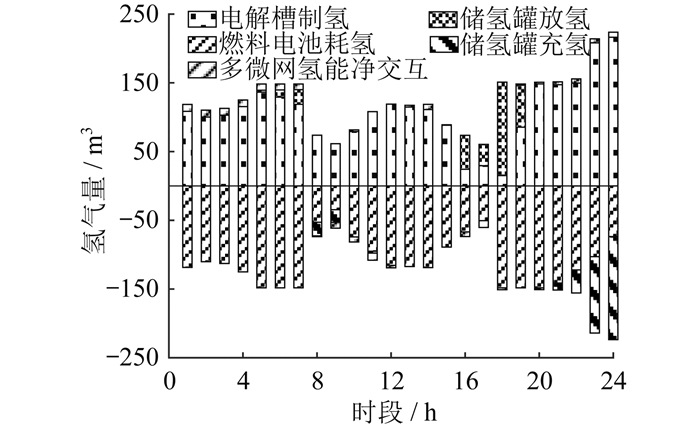
图 5为SHES的氢能优化运行结果。
从图 5可知, 由于MG1和MG3倾向于在00:00—08:00和16:00—24:00时段向SHES售电, MG2倾向于在09:00—15:00时段向SHES售电, 各微电网售电时段存在互补关系, 故SHES的电解槽装置在全天所有时段将从各微电网购入的电能用于制氢。同样, 由于MG1倾向于在08:00—18:00时段向SHES购电, MG2倾向于在00:00—08:00和16:00—24:00时段向SHES购电, 各微电网购电时段也存在一定的互补关系, 故SHES的燃料电池也在全天所有时段将存储的氢气用于发电并对外出售。此外, 储氢罐主要选择在16:00—20:00时段放氢, 在20:00—24:00时段充氢。这是因为在16:00—20:00时段, 微电网群整体呈现缺电状态, 多电微电网的售电量不足以满足缺电微电网的购电需求, 故储氢罐需释放部分氢气用于发电, 而在20:00—24:00时段, 微电网群整体呈现多电状态, 多电微电网的售电量能够满足缺电微电网的购电需求, 故储氢罐选择充入多余的氢气以保证其储氢量在调度周期内维持一定的平衡。总体来说, 微电网群通过共享氢储能间接实现了电能和氢能的交互, 促进了能源的就地消纳, 提高了能源的使用效率。
3.3 经济分析
为验证本文所提方案的有效性, 设置以下3种方案进行对比分析。方案1:各微电网通过SHES实现合作运行, 并考虑燃气掺氢(本文所提方案)。方案2:不考虑加入SHES, 即各微电网独立运行, 并考虑燃气掺氢。方案3:各微电网通过SHES实现合作运行, 但不考虑燃气掺氢。
3.3.1 微电网与上级网络的能源交互分析
表 5为不同方案下各微电网与上级网络能源交互情况。
表 5
不同方案下各微电网与上级网络能源交互情况
| 方案 | 微电网 | 购电功率/kW | 售电功率/kW | 购气量/m3 | 能源交互总成本/元 | 新能源消纳率 /% |
| 1 | MG1 | 21.7 | 344.1 | 2 260.1 | 6 709.5 | 96.8 |
| MG2 | 588.8 | 0 | 2 343.6 | 7 564.2 | 100.0 | |
| MG3 | 0 | 69.5 | 2 545.6 | 7 619.4 | 99.5 | |
| 2 | MG1 | 2 686.8 | 3 187.4 | 2 142.6 | 7 984.4 | 70.4 |
| MG2 | 5 962.8 | 2 326.9 | 2 510.4 | 11 594.4 | 65.5 | |
| MG3 | 0 | 3 749.2 | 2 366.8 | 6 163.1 | 70.3 | |
| 3 | MG1 | 70.8 | 688.7 | 2 372.3 | 6 994.4 | 93.6 |
| MG2 | 594.6 | 301.3 | 2 509.4 | 7 887.3 | 95.5 | |
| MG3 | 0 | 835.2 | 2 584.6 | 7 545.0 | 93.4 |
由表 5可知, 对比方案2, 方案1中各微电网向上级电网的售电功率分别降低了2 843.3 kW、2 326.9 kW、3 679.7 kW, 新能源消纳率分别提升了26.4%、34.5%、29.2%, 微电网群与上级能源网络的能源交互总成本降低了3 848.8元。可见, SHES的加入能够促进微电网之间的能量共享, 提高能源的就地消纳率, 减少各微电网对于上级网络的能源依赖, 实现多微电网的互利共赢。对比方案3, 方案1中各微电网向上级电网的售电功率分别降低了344.6 kW、301.3 kW、765.7 kW, 各微电网向上级气网的购气量分别降低了112.2 m3、165.8 m3、39.0 m3, 新能源消纳率分别提升了3.2%、4.5%、6.1%, 微电网群与上级能源网络的能源交互总成本降低了533.6元。可见, 考虑燃气掺氢同样有利于提高各微电网新能源消纳率, 降低微电网群能源交互总成本。这是因为燃气掺氢后各微电网会优先将风光资源用于电解槽制氢, 促进了新能源的消纳。此外, 氢能需求的增加也会使得CHP机组的电热出力有所增加, 进而导致燃气锅炉的热出力有所降低, 虽然CHP机组的购气量有所增加, 但燃气锅炉的购气量则降低得更多。总体而言, 燃气掺氢降低了各微电网与上级电网、气网的能源交互量, 有利于提升各微电网的新能源消纳率。
3.3.2 微电网碳排放分析
表 6为不同方案下各微电网的碳排放情况。
表 6
不同方案下各微电网碳排放情况
| 方案 | 微电网 | 碳排放量/kg | 碳排放成本/元 |
| 1 | MG1 | 15 995.4 | 4 030.9 |
| MG2 | 17 089.8 | 4 306.6 | |
| MG3 | 17 994.2 | 4 534.5 | |
| 2 | MG1 | 17 534.1 | 4 418.6 |
| MG2 | 23 046.4 | 5 807.7 | |
| MG3 | 16 730.2 | 4 216.0 | |
| 3 | MG1 | 16 832.3 | 4 241.7 |
| MG2 | 18 178.3 | 4 580.9 | |
| MG3 | 18 269.9 | 4 604.0 |
相较于方案2, 方案1考虑了微电网之间的合作。由表 6可知, MG1、MG2的碳排放量有所降低, 而MG3的碳排放量有所增加。这是因为MG3为了在电氢能源共享中赚取更多收益, 增大了CHP机组的出力, 进而使得其向上级气网购买的天然气量也有所升高, 故其碳排放量升高。相反, MG1和MG2通过部分共享购能代替了自身机组的出力, 故其购气量有所降低, 碳排放量也因此降低。相较于方案3, 方案1考虑了燃气掺氢。根据前文分析可知, 燃气掺氢有助于降低微电网向上级网络的购电量和购气量, 故MG1、MG2和MG3的碳排放量以及碳排放成本均有所降低, 由此也验证了本文所提方案的经济性和低碳性。
3.3.3 合作前后各主体收益对比分析
表 7和表 8分别为合作前后各微电网的运营成本和SHES的运营收益结果。
表 7
各微电网合作前后成本
| 微电网 | 合作前运营成本 | 合作后运营成本 | 与SHES交易成本 | 最终成本 |
| MG1 | 12 937.6 | 11 294.5 | 391.0 | 11 685.5 |
| MG2 | 18 007.8 | 12 440.5 | 4 316.8 | 16 757.3 |
| MG3 | 10 969.3 | 12 784.7 | -3 068.8 | 9 715.9 |
表 8
SHES合作前后收益
| 合作前运营收益 | 合作后运营收益 | 与微电网群交易收益 | 最终收益 |
| 0 | -385.6 | 1 638.2 | 1 252.6 |
由表 7和表 8可知, MG1、MG2和MG3在合作运行后的运行成本分别降低了1 252.1元、1 250.5元和1 253.4元, SHES的运行收益则提升了1 252.6元。由此可知, SHES的加入使得各微电网在能量共享上得到了充分的合作, 无论是微电网还是SHES, 参与合作的各主体的效益均得到了改善。此外, SHES与微电网群组成合作联盟后整体效益提升了5 009.4元, 基于纳什议价方法对合作收益进行再次分配, 使得各参与主体效益提升十分相近, 约为1 252.4元, 这也体现了纳什谈判理论在处理合作剩余分配问题上的公平性。
4 结论
本文以SHES和微电网群为研究对象, 提出一种含SHES的园区综合能源微电网群低碳协同运行方法, 通过算例仿真, 得出以下结论。
(1) 相较于各微电网独立运行, 多个微电网通过SHES实现电氢能源的交互和共享, 能够进一步提升新能源的就地消纳率和系统运行经济性。
(2) 基于纳什谈判理论对多主体合作剩余进行分配, 使得各参与者得到了近乎平均的收益提升, 体现了纳什议价在处理此类问题上的公平性。
(3) 考虑燃气掺氢, 同样有助于提升新能源的消纳率, 同时能够降低各微电网的碳排放量, 进而降低微电网的运行成本。
参考文献
-
[1]张显, 史连军. 中国电力市场未来研究方向及关键技术[J]. 电力系统自动化, 2020, 44(16): 1-11.
-
[2]骆钊, 刘德文, 沈鑫, 等. 综合能源系统优化运行技术研究综述[J]. 电力建设, 2022, 43(12): 3-14.
-
[3]吴锦领, 楼平, 管敏渊, 等. 基于非对称纳什谈判的多微网电能共享运行优化策略[J]. 电网技术, 2022, 46(7): 2711-2723.
-
[4]顾欣, 王琦, 胡云龙, 等. 基于纳什议价的多微网综合能源系统分布式低碳优化运行策略[J]. 电网技术, 2022, 46(4): 1464-1482.
-
[5]程静, 谭智钢, 岳雷. 考虑负荷综合需求响应的CCHP-SESS双层优化配置[J]. 电网技术, 2023, 47(3): 918-931.
-
[6]王开艳, 梁岩, 贾嵘. 考虑共享储能的冷热电联供型微网低碳经济调度[J]. 电网与清洁能源, 2022, 38(11): 155-162.
-
[7]李笑竹, 陈来军, 殷骏, 等. 面向低碳供能的多园区共享氢储能系统容量规划[J]. 高电压技术, 2022, 48(7): 2534-2544.
-
[8]任洲洋, 罗潇, 覃惠玲, 等. 考虑储氢物理特性的含氢区域综合能源系统中长期优化运行[J]. 电网技术, 2022, 46(9): 3324-3333.
-
[9]王文烨, 姜飞, 张新鹤, 等. 含规模氢能综合利用的高比例风光多能源系统低碳灵活调度[J/OL]. 电网技术, 2023: 1-15. [2023-09-27]. http://fx.shieplib.chaoxing.com/detail-38502727.
-
[10]吴盛军, 李群, 刘建坤, 等. 基于储能电站服务的冷热电多微网系统双层优化配置[J]. 电网技术, 2021, 45(10): 3822-3832.
-
[11]帅轩越, 马志程, 王秀丽, 等. 基于主从博弈理论的共享储能与综合能源微网优化运行研究[J]. 电网技术, 2023, 47(2): 679-690.
-
[12]帅轩越, 王秀丽, 吴雄, 等. 计及电热需求响应的共享储能容量配置与动态租赁模型[J]. 电力系统自动化, 2021, 45(19): 24-32.
-
[13]胡洁, 李培强, 林仕满, 等. 考虑分时电价差异性和基于主从博弈的智能楼宇集群能量共享方法[J]. 电网技术, 2021, 45(12): 4738-4750.
-
[14]陈曦, 付文龙, 张海荣, 等. 考虑新能源发电不确定性的含微电网群共享储能优化调度[J/OL]. 电网技术, 2023: 1-17. [2023-09-27]. http://fx.shieplib.chaoxing.com/detail-38502727.
-
[15]郭宴秀, 苏建军, 刘洋, 等. 考虑电热交互和共享储能的多综合能源系统运行优化[J]. 中国电力, 2023, 56(4): 138-145.
-
[16]陈登勇, 刘方, 刘帅. 基于阶梯碳交易的含P2G-CCS耦合和燃气掺氢的虚拟电厂优化调度[J]. 电网技术, 2022, 46(6): 2042-2054.
-
[17]马腾飞, 裴玮, 肖浩, 等. 基于纳什谈判理论的风-光-氢多主体能源系统合作运行方法[J]. 中国电机工程学报, 2021, 41(1): 25-39.