|
|
|
发布时间: 2023-10-28 |
综合能源 |
|
|
|
收稿日期: 2023-06-01
中图法分类号: TM73
文献标识码: A
文章编号: 2096-8299(2023)04-0426-10
|
摘要
为了分析分布式新能源和需求侧灵活响应资源的不确定性对综合能源系统(IES)的影响: 首先, 建立了IES灵活性供需模型; 其次, 构建了基于场景概率驱动的IES两阶段分布鲁棒优化模型; 最后, 采用列与约束生成算法进行迭代求解, 通过仿真验证了该模型和求解算法的有效性。相较于传统的IES优化调度, 其所提模型减少了系统的总运行成本, 提升了系统的灵活性。
关键词
综合能源系统; 分布鲁棒; 灵活性; 不确定性; 数据驱动; 列与约束生成算法
Abstract
In order to better consider the impact of the uncertainty of distributed new energy sources and the demand-side flexible response resources on the integrated energy system, firstly, the IES flexibility supply and demand model is established.Secondly, the IES two-stage distributed robust optimization model is constructed based on scenario probability driven.Finally, the Column and Constraint Generation (CCG) algorithm is used for iterative solution.The effectiveness of the proposed model and solution algorithm is verified by simulation analysis.Compared with traditional IES optimization scheduling, the model proposed in this paper reduces the total operating cost of the system and improves the flexibility of the system.
Key words
integrated energy system; distributed robust; flexibility; uncertainty; data-driven; column and constraint generation
分布式电源(Distributed Generation, DG)出力和需求响应的不确定性易导致系统灵活性出现供需不平衡的现象, 会对系统的稳定与安全运行产生巨大影响[1]。随机优化[2-3]和鲁棒优化[4-5]是处理不确定性问题的两种有效手段, 但是随机优化往往需要大量的离散场景, 决策精度取决于统计数量, 而鲁棒优化结果又太过保守。分布鲁棒优化(Distributed Robust Optimal, DRO)在处理不确定性参数时结合了上述两种方法的优点, 寻找最恶劣场景下的概率分布。传统分布鲁棒方法计算复杂, 需要利用矩信息表征概率分布场景, 再通过拉格朗日对偶转化将问题转化为半定规划问题[6]。基于数据驱动的分布鲁棒方法因其可以利用不确定变量的历史信息这一特点, 现已在无功优化[7]、输电规划[8]、储能规划[9]、电力系统优化调度[10]等领域得到应用, 但在综合能源系统(Integrated Energy System, IES)优化运行方面的应用仍相对匮乏。因此, 将基于数据驱动的分布鲁棒方法引入到IES优化运行中具有重要价值。
近年来, 越来越多的国内外学者将需求响应(Demand Response, DR)考虑到IES优化中。文献[11]提出了以电价需求响应为驱动的多能源协同系统的优化模型, 将风电、光伏、热电联产机组的出力根据能量枢纽模型调整, 加入储能设备与DR。文献[12]采用蓄热装置提升供热灵活性, 不同时间尺度下转移电、热负荷, 充分发挥负荷侧灵活性资源的作用。文献[13]根据电热联合需求响应, 建立日内滚动优化模型解决日前调度存在偏差的问题。文献[14]提出一种考虑用户响应特性的优化激励模型, 求解能源服务商收益和用户成本最优策略。以上文献均在确定性DR的基础上进行IES优化调度[11-14], 并未考虑DR的不确定性, 也未研究激励措施对系统灵活性调节的影响。需求侧资源从用能侧为IES的灵活运行提供另一种调整方案, 对于提升系统经济性收效显著[15]。文献[16]考虑区域间多种灵活性资源的协同互济, 并采用条件风险价值量化灵活性不足风险成本, 建立了多区域间的协调调度策略。文献[17]利用多种类型的电源消纳风电, 实现了多种电源的分层优化协调。文献[18]建立了电-气-热互联运行模型, 兼顾了网络的动态特性和运行灵活性约束。
上述文献均未考虑一定时间内系统灵活性需求变化对灵活性供给爬坡调整的影响, 也未深入挖掘DG出力的不确定性和用能侧响应资源的不确定性在IES的双向互动能力。因此, 本文首先从风电、光伏(以下简称“风光”)和需求响应的不确定性角度, 建立计及灵活性需求偏差的灵活性供需平衡; 其次, 采用基于数据驱动的分布鲁棒方法处理风光出力和需求响应的不确定性, 建立计及灵活性需求偏差的两阶段分布鲁棒优化调度模型; 最后, 通过相应算例分析所提模型的有效性, 通过设置不同金额补贴价格分析其对IES灵活性的影响, 并与随机优化和鲁棒优化的结果进行对比。
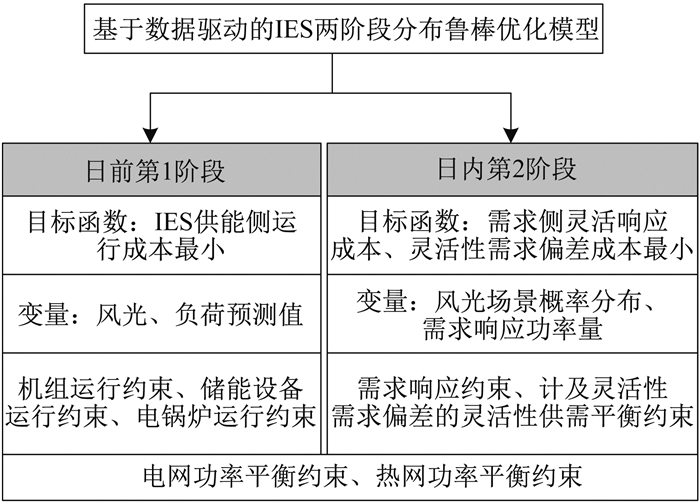
1 IES分布鲁棒优化框架
2 IES灵活性建模
2.1 IES灵活性供给模型
IES灵活性供给来源包括燃气轮机和储能设备, 灵活性需求根据用户对负荷的调度进行变化。当系统灵活性不足时, 燃气轮机上调出力以提高系统灵活性, 但爬坡约束会限制相邻时段的灵活性变化幅度, 此时储能装置替燃气轮机承担一部分灵活性供给, 进行放电。当系统灵活性充裕时, 储能装置更多处于充电状态, 但储能装置受其功率约束的限制, 提升灵活性能力依旧有限。灵活性供给模型[19]为
| $ \left\{\begin{aligned} S_{t, +} & =\min \left(P_{\max }^{\mathrm{G}}-P_{t}^{\mathrm{G}}, \tau R_{+}\right) \\ & +\min \left(P_{\max }^{\mathrm{ES}}-P_{t}^{\mathrm{ES}}, \frac{E_{\max }^{\mathrm{ES}}-E_{t}^{\mathrm{ES}}}{\tau}\right) \\ S_{t, -} & =\min \left(P_{t}^{\mathrm{G}}-P_{\text {min }}^{\mathrm{G}}, \tau R_{-}\right) \\ & +\min \left(P_{t}^{\mathrm{ES}}-P_{\text {min }}^{\mathrm{ES}}, \frac{E_{t}^{\mathrm{ES}}-E_{\min }^{\mathrm{ES}}}{\tau}\right) \end{aligned}\right. $ | (1) |
式中: St, +、St, -——IES在t时刻的上行和下行灵活性供给;
PmaxG、PminG——微型燃气轮机的电出力上限和下限值;
PtG——微型燃气轮机在t时刻的电功率;
τ——调度时间间隔;
R+、R-——微型燃气轮机爬坡和滑坡速率;
PmaxES、PminES——储能装置充放能功率的上限和下限值;
PtES——储能装置t时刻充放能功率;
EmaxES、EminES——储能量上限和下限值;
EtES——储能装置t时刻储能量。
2.2 IES灵活性需求偏差
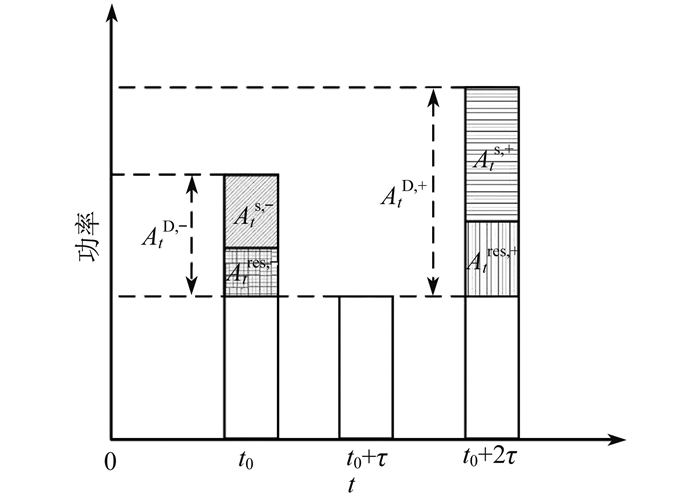
新能源出力不确定性会引起系统灵活性波动, 对其安全稳定运行带来一定的风险。风光作为电源, 若出力向上波动, 系统则产生一定量的上行灵活性需求, 当风光出力在一定时间内持续向上波动, 即新能源当前时段的实际功率大于日前决策功率, 系统内的燃气轮机和储能等灵活性设备因为其爬坡的限制不能及时填补系统缺失的灵活性, 系统内则会产生大量的灵活性不足, 还会出现弃风、弃光现象; 相反, 若风光出力向下产生波动, 系统则产生一定量的下行灵活性需求, 当新能源出力在一定时间内持续产生向下的波动, 即风光当前时段的实际功率小于日前决策功率, 系统内的灵活性设备受到爬坡约束无法快速减少对系统的灵活性供给, 则会导致风光资源利用不足。
风光不确定性导致的这两种现象均对IES灵活性供需平衡产生巨大影响。同时, 用户响应量会受到环境、心理和经济等诸多因素的影响。需求侧灵活响应资源作为负载, 对系统灵活性上行和下行的影响与风光恰恰相反。当需求响应功率量向上波动, 系统产生一些下行灵活性需求; 当需求响应功率量向下波动, 系统则产生一些上行灵活性需求。因此需求侧响应不确定性引起的灵活性需求变化不可忽视。为量化风光不确定性和需求响应不确定性对系统灵活性需求的影响, 对IES灵活性需求偏差进行量化, 可描述为
| $ \left\{\begin{array}{l} A_{t}^{\mathrm{D}, +}=A_{t}^{\mathrm{s}, +}+A_{t}^{\mathrm{res}, +} \\ A_{t}^{\mathrm{D}, -}=A_{t}^{\mathrm{s}, -}+A_{t}^{\mathrm{res}, -} \end{array}\right. $ | (2) |
| $ \left\{\begin{array}{l} A_{t}^{\mathrm{s}, +}=P_{t}^{\mathrm{s}, \text { real }}-P_{t}^{\mathrm{s}, \text { pre }} \\ A_{t}^{\mathrm{s}, -}=P_{t}^{\mathrm{s}, \text { pre }}-P_{t}^{\mathrm{s}, \text { real }} \end{array}\right. $ | (3) |
| $ \left\{\begin{array}{l} A_{t}^{\mathrm{res}, +}=P_{t}^{\mathrm{res}, \text { real }}-P_{t}^{\mathrm{res}, \text { pre }} \\ A_{t}^{\mathrm{res}, -}=P_{t}^{\mathrm{res}, \text { pre }}-P_{t}^{\mathrm{res}, \text { real }} \end{array}\right. $ | (4) |
| $ P_{t}^{\mathrm{s}}=P_{t}^{\mathrm{shift}}-P_{t}^{\text {reduce }}-\lambda^{\mathrm{eh}} H^{\text {reduce }} $ | (5) |
式中: AtD, +、AtD, -——IES在t时刻的灵活性需求上行和下行偏差;
Ats, +、Ats, -——t时刻需求响应不确定性引起的灵活性需求上行和下行偏差;
Atres, +、Atres, -——新能源出力在t时刻的波动引起的灵活性需求上行和下行偏差;
Pts, real——t时刻实际需求响应功率;
Pts, pre——需求响应功率日前预测值;
Ptres, real——新能源t时刻实际出力;
Ptres, pre——新能源日前决策出力;
Pts——需求响应功率;
Ptshift、Ptreduce——t时段内转移电负荷量和中断电负荷量;
λeh——热电转换系数;
Htreduce——t时段内可消减热负荷的功率量。
不同调度时间段灵活性需求偏差示意如图 2所示。
则t时刻的灵活性需求偏差成本可定义为
| $ C_{t}^{\mathrm{dev}}=\left\{\begin{array}{l} c_{\mathrm{f}}^{+}\left(u^{\mathrm{s}, +} A_{t}^{\mathrm{s}, +}+u^{\mathrm{res}, +} A_{t}^{\mathrm{res}, +}\right) \\ c_{\mathrm{f}}^{-}\left(u^{\mathrm{s}, -} A_{t}^{\mathrm{s}, -}+u^{\mathrm{res}, -} A_{t}^{\mathrm{res}, -}\right) \end{array}\right. $ | (6) |
式中: Ctdev——IES灵活性需求偏差成本;
cf+、cf-——上行和下行偏差惩罚系数;
us, +、us, -——用户响应负荷的上行和下行偏差标志位(当Pts, real≥Pts, pre时, us, +取1, us, -取零; 反之, us, -取1, us, +取零);
ures, +、ures, -——新能源出力的上行和下行偏差标志位(当Ptres, real≥Ptres, pre时, ures, +取1, ures, -取零; 反之ures, -取1, ures, +取零)。
2.3 IES灵活性需求模型
能源运营商在较低系统灵活性时段来临前, 将负荷转移到较高系统灵活性时段或者切断一些负荷, 提高系统灵活性余量。
灵活性需求定义为
| $ \begin{gathered} \left\{\begin{array}{c} D_{t, +}=\max \left(A_{t}^{\mathrm{D}, +}, 0\right) \\ D_{t, -}=\max \left(A_{t}^{\mathrm{D}, -}, 0\right) \end{array}\right. \\ \end{gathered} $ | (7) |
| $ P_{t}^{\mathrm{D}}=P_{t}^{\mathrm{L}}-P_{t}^{\mathrm{res}} $ | (8) |
式中: Dt, +、Dt, -——t时刻IES的上行和下行灵活性需求;
PtD、PtL、Ptres——t时刻功率需求量、电负荷和新能源电出力。
当IES初始灵活性需求量等于调度时段末灵活性需求量, 可表示为
| $ \begin{gathered} P_{0}^{\mathrm{D}}+\sum\limits_{t=1}^{\mathrm{T}}\left(u^{\mathrm{s}, +} A_{t}^{\mathrm{s}, +}+u^{\mathrm{s}, -} A_{t}^{\mathrm{s}, -}+u^{\mathrm{res}, +} A_{t}^{\mathrm{res}, +}+\right. \\ \left.u^{\mathrm{res}, -} A_{t}^{\mathrm{res}, -}\right)=P_{\mathrm{T}}^{\mathrm{D}} \end{gathered} $ | (9) |
式中: P0D——初始功率需求量;
PTD——调度时段末功率需求量。
根据风光不确定性出力特性和用户需求侧响应不确定性负荷变化引起的灵活性需求偏差, 可以建立计及灵活性需求偏差的IES灵活性供需平衡约束, 描述为
| $ \left\{\begin{array}{l} \Delta E_{t, +}=S_{t, +}-D_{t, +} \\ \Delta E_{t, -}=S_{t, -}-D_{t, -} \end{array}\right. $ | (10) |
式中: ΔEt, +、ΔEt, -——t时刻IES的上行和下行灵活性余量。
ΔEt, +、ΔEt, -取值越大, 表明灵活性供给能力越充足; 反之, 则表明灵活性供给能力越匮乏。
3 IES两阶段分布鲁棒优化模型
3.1 目标函数
3.1.1 日前第1阶段目标函数
日前第1阶段目标函数F1为IES供能侧的运行成本, 包括微型燃气轮机发电成本CtG和储能设备运维成本CtES, 为
| $ \min F_{1}=\sum\limits_{t=1}^{\mathrm{T}}\left(C_{t}^{\mathrm{G}}+C_{t}^{\mathrm{ES}}\right) $ | (11) |
微型燃气轮机发电成本为
| $ C_{t}^{\mathrm{G}}=a\left(P_{t}^{\mathrm{G}}\right)^{2}+b P_{t}^{\mathrm{G}}+c $ | (12) |
式中: a、b、c——微燃机发电成本系数。
储能装置运维成本为
| $ C_{t}^{\mathrm{ES}}=c^{\mathrm{ES}}\left(P_{t}^{\mathrm{ES}, \mathrm{c}}+P_{t}^{\mathrm{ES}, \mathrm{d}}\right) $ | (13) |
式中: cES——储能装置充电放电功率单位成本系数;
PtES, c、PtES, d——储能装置充电和放电功率。
3.1.2 日内第2阶段目标函数
日内第2阶段的目标函数F2包括需求侧灵活响应成本Cts和灵活性需求偏差成本Ctdev, 为
| $ \min F_{2}=\sum\limits_{t=1}^{\mathrm{T}}\left(C_{t}^{\mathrm{s}}-C_{t}^{\mathrm{dev}}\right) $ | (14) |
需求侧灵活响应成本为
| $ C_{t}^{\mathrm{s}}=p^{\mathrm{s}}\left(P_{t}^{\text {shift }}+P_{t}^{\text {reduce }}+\lambda^{\text {eh }} H_{t}^{\text {reduce }}\right) $ | (15) |
式中: ps——用户参与需求响应的补贴价格。
3.2 约束条件
3.2.1 需求响应约束
可转移电负荷为
| $ \sum\limits_{t=\alpha_{\mathrm{e}}}^{\beta_{\mathrm{e}}} u_{t}^{\text {shift }}=T^{\text {shift }}, t \in\left[\alpha_{\mathrm{e}}, \beta_{\mathrm{e}}\right] $ | (16) |
| $ P_{t}^{\text {shift }} \leqslant P_{\mathrm{e}}^{\text {shift }} $ | (17) |
式中: utshift——二进制变量, 表示参与转移电负荷状态;
Tshift——总转移时间间隔;
[αe, βe]——用户转移电负荷限定时间范围;
Peshift——可转移负荷用户的转移额定功率。
可中断电负荷为
| $ \left\{\begin{array}{l} \Delta P_{t}^{\text {reduce }}=P_{0}^{\text {reduce }}-P_{t}^{\text {reduce }} \\ P_{\min }^{\text {reduce }} \leqslant P_{t}^{\text {reduce }} \leqslant P_{\max }^{\text {reduce }} \end{array}\right. $ | (18) |
式中: ΔPtreduce——中断电负荷变化量;
P0reduce——中断前电负荷;
Pmaxreduce、Pminreduce——可转移电负荷上限和下限功率量。
可削减热负荷为
| $ T_{\mathrm{in}, t+1}=T_{\mathrm{out}, t}+\left(T_{\mathrm{in}, t}-T_{\mathrm{out}, t}\right) \mathrm{e}^{-\frac{\tau}{R C}}+ \\ \qquad\qquad H_{t}^{\text {reduce }} R\left(1-\mathrm{e}^{-\frac{\tau}{R C}}\right) $ | (19) |
| $ \left\{\begin{array}{l} 0 \leqslant H_{t}^{\text {reduce }} \leqslant H_{\mathrm{max}}^{\text {reduce }} \\ T_{\mathrm{in}, \min } \leqslant T_{\mathrm{in}, t} \leqslant T_{\mathrm{in}, \max } \\ T_{\mathrm{in}, t}=T_{\mathrm{in}, 0}, T_{\text {out }, t}=T_{\text {out }, 0} \end{array}\right. $ | (20) |
式中: Tin, t、Tout, t——t时段室内和室外温度;
R——住宅建筑外部热阻;
C——室内空气比热容;
Htreduce——削减热负荷量(可正可负), 其值为正时加热、为负时制冷;
Hmaxreduce——可削减热负荷量上限值;
Tin, max、Tin, min——室内温度上限和下限;
Tin, 0、Tout, 0——初始时刻室内和室外温度。
3.2.2 电网功率平衡约束
电网功率平衡约束计算公式为
| $ P_{t}^{\mathrm{G}}+P_{t}^{\mathrm{res}}+P_{t}^{\mathrm{ES}, \mathrm{d}}=P_{t}^{\mathrm{EB}}+P_{t}^{\mathrm{ES}, \mathrm{c}}+P_{t}^{\mathrm{L}} $ | (21) |
式中: Ptres——t时刻新能源电出力;
PtES, d、PtES, c——t时刻储电装置放电和充电功率;
PtEB——t时刻电锅炉消耗电功率;
PtL——t时刻电负荷。
3.2.3 热网功率平衡约束
热网功率平衡约束的计算公式为
| $ H_{t}^{\mathrm{G}}+H_{t}^{\mathrm{EB}}+H_{t}^{\mathrm{ES}, \mathrm{d}}=H_{t}^{\mathrm{ES}, \mathrm{c}}+H_{t}^{\mathrm{L}} $ | (22) |
式中: HtG——t时刻微型燃气轮机热功率;
HtEB——t时刻电锅炉热功率;
HtES, d、HtES, c——t时刻储热装置放热和充热功率;
HtL——t时刻热负荷。
其余系统内灵活性资源常规约束, 如机组运行约束、储能运行约束和电锅炉约束详见文献[20]。
3.3 两阶段DRO模型
基于新能源和需求响应历史数据, 建立两阶段DRO模型为
| $ \min\limits_{\boldsymbol{x} \in \mathit{\boldsymbol{X}}} F_{1}(\boldsymbol{x})+\max\limits_{p_{k} \in {\mathit{\Omega}}} \sum\limits_{k=1}^{K} p_{k} \min\limits_{\boldsymbol{y}_{k} \in Y\left(x, \xi_{k}\right)} F_{2}\left(\boldsymbol{x}, \boldsymbol{y}_{k}, \boldsymbol{\xi}_{k}\right) $ | (23) |
式中: x——日前第1阶段变量;
X——日前第1阶段变量集合;
pk——第k个场景出现概率;
Ω——综合范数满足的模糊集合;
K——离散场景个数;
yk——第k个场景下的第2阶段变量;
y——日内第2阶段变量;
Y(x, ξk)——第k个场景下的日内第2阶段变量;
Y——第k个场景下日内第2阶段变量集合;
ξk——第k个场景下DG出力和需求响应功率量。
日前第1阶段约束条件为
| $ \text { s. t. } \mathit{\boldsymbol{Cx}} \leqslant \mathit{\boldsymbol{c}} $ | (24) |
式中: C、c——约束条件中对应第1阶段变量的矩阵或向量。
日内第2阶段的约束条件为
| $ \boldsymbol{D} \boldsymbol{y}_{k} \leqslant \boldsymbol{d}, \quad \forall k $ | (25) |
| $ \boldsymbol{E} \boldsymbol{y}_{k} \leqslant \boldsymbol{e}, \quad \forall k $ | (26) |
式中: D、E、d、e——约束条件中对应日内第2阶段变量的矩阵或向量。
采取场景概率驱动方法。首先, DG出力和需求响应功率量的数据样本在预测数据的基础上, 利用拉丁超立方采样方法进行分层采样, 误差服从正态分布, 方差均值取零。预测值取20%, 并将Cholesky分解法作为相关性控制方法[21]。针对风光和需求响应的M个实际历史场景, 通过基于概率距离的场景削减技术, 削减得出K个有限离散场景(如ξ1, ξ2, ξ3, …, ξK), 以表征各个场景下的DG和需求响应功率, 典型场景集合S={S1, S2, S3, …, SK}, 其中第k个典型场景Sk包含Mk个历史场景, 继而构造不确定性变量的初始概率分布p0=(p10, p20, p30, …, pK0), 其中pk0=Mk/M(k=1, 2, 3, …, K), 为第k个典型场景发生的概率。但初始概率分布p0与实际概率分布p有所不同, 因此为保证场景概率分布的取值在合理范围内, 采用综合范数模糊集[22], 构建以上述初始概率分布为中心的综合范数约束, 为
| $ \left\{\begin{array}{l} {\mathit{\Omega}}=\left\{p_{k} \mid p_{k} \geqslant 0, k=1, 2, 3, \cdots, K\right\} \\ \sum\limits_{k=1}^{K} p_{k}=1 \\ \sum\limits_{k=1}^{K}\left|p_{k}-p_{k}^{0}\right| \leqslant \theta_{1} \\ \max\limits_{1 \leqslant k \leqslant K}\left|p_{k}-p_{k}^{0}\right| \leqslant \theta_{\infty} \end{array}\right. $ | (27) |
式中: pk0——初始场景概率分布值;
θ1、θ∞——1-范数和∞-范数约束下的允许概率分布偏差限值。
概率分布{pk} 满足文献[23]的置信度约束, 为
| $ \left\{\begin{array}{l} \operatorname{Pr}\left\{\sum\limits_{k=1}^{K}\left|p_{k}-p_{k}^{0}\right| \leqslant \theta_{1}\right\} \geqslant 1-2 K \mathrm{e}^{\frac{-2 M \theta_{1}}{K}} \\ \operatorname{Pr}\left\{\max\limits_{1 \leqslant k \leqslant K}\left|p_{k}-p_{k}^{0}\right| \leqslant \theta_{\infty}\right\} \geqslant 1-2 K \mathrm{e}^{\frac{-2 M \theta_{\infty}}{K}} \end{array}\right. $ | (28) |
式中: Pr——概率。
令不确定性概率置信水平α1和α∞分别等于1-2Ke-2Mθ1/K和1-2Ke-2Mθ∞/K, 则在95%置信水平和式(28)的置信度约束条件下, 保证了模糊分布在给定集合内至少有95%的可能性存在。θ1和θ∞可根据式(29)进行计算[24], 为
| $ \left\{\begin{array}{l} \theta_{1}=\frac{K}{2 M} \ln \frac{2 K}{1-\alpha_{1}} \\ \theta_{\infty}=\frac{1}{2 M} \ln \frac{2 K}{1-\alpha_{\infty}} \end{array}\right. $ | (29) |
式中: M——历史数据样本个数。
场景概率可以偏离初始场景概率的最大值, 其值越大, 鲁棒模型越保守; 反之, 则风险越大。
4 模型求解
式(23)中的两阶段分布鲁棒调度问题为min-max-min 3层优化问题, 不能直接求解, 故采用列与约束生成算法, 将问题拆分为主问题(Master Problem, MP)和子问题(Sub-Problem, SP)进行迭代求解。
主问题求解过程中不考虑不确定变量, 为确定性优化问题, 求解子问题时向主问题添加辅助变量和约束条件, 不断更新目标函数的上界和下界, 反复迭代直至收敛。
4.1 主问题MP
MP是在场景概率分布已知的基础上, 得出满足供能侧运行成本最优的最优解, 为
| $ \mathrm{MP}: \min\limits_{x \in X, y_{k}^{m} \in Y\left(x, \xi_{k}\right), \eta} \boldsymbol{A x}+\eta $ | (30) |
| $ \begin{array}{*{20}{c}} {\text { s.t. } \eta \geqslant \max\limits_{p_{k} \in {\mathit{\Omega}}} \sum\limits_{k=1}^{K} p_{k}^{m *} \min\limits_{y_{k}^{m} \in Y\left(x, \xi_{k}\right)}\left(\boldsymbol{B} \boldsymbol{y}_{k}+\boldsymbol{L} \boldsymbol{\xi}_{k}\right), }\\ {\forall m=1, 2, 3, \cdots, n } \end{array} $ | (31) |
| $ \boldsymbol{C} \boldsymbol{x} \leqslant \boldsymbol{c} $ | (32) |
| $ \boldsymbol{D} \boldsymbol{y}_{k}^{m} \leqslant \boldsymbol{d}, \forall k, \forall m=1, 2, 3, \cdots, n $ | (33) |
| $ \boldsymbol{E} \boldsymbol{y}_{k}^{m} \leqslant \boldsymbol{e}, \forall k, \forall m=1, 2, 3, \cdots, n $ | (34) |
式中: A——第1阶段变量的系列矩阵;
B——第2阶段变量的系列矩阵;
L——不确定变量的系列矩阵;
上标“*”——相应变量最优解;
η——给定阈值;
N——迭代次数。
4.2 子问题SP
给定日前第1阶段变量x*后, 对SP进行求解, 为
| $ \begin{aligned} \mathrm{SP}: f_{\mathrm{SP}}\left(\boldsymbol{x}^{*}\right)= & \max\limits_{p_{k} \in {\mathit{\Omega}}} \sum\limits_{k=1}^{K} p_{k}^{m} \min\limits _{y^{m}_{k} \in {Y}\left(x, \xi_{k}\right)}\left(\boldsymbol{B} \boldsymbol{y}_{k}+\boldsymbol{L} \boldsymbol{\xi}_{k}\right), \\ & \forall m=1, 2, 3, \cdots, n\end{aligned} $ | (35) |
在子问题中, 由于外部最大值问题的场景概率分布值不参与内部最小值问题, 其与内部最小值问题的日内第2阶段变量之间相互独立, 故无需进行对偶转换, 可将子问题分为两步进行并行求解[24]。
4.3 求解流程
第1步为求解子问题中内部最小值问题, 第2步为求解子问题中外部最大值问题。数据驱动DRO求解流程如图 3所示。
5 算例分析
5.1 预测曲线与场景分析
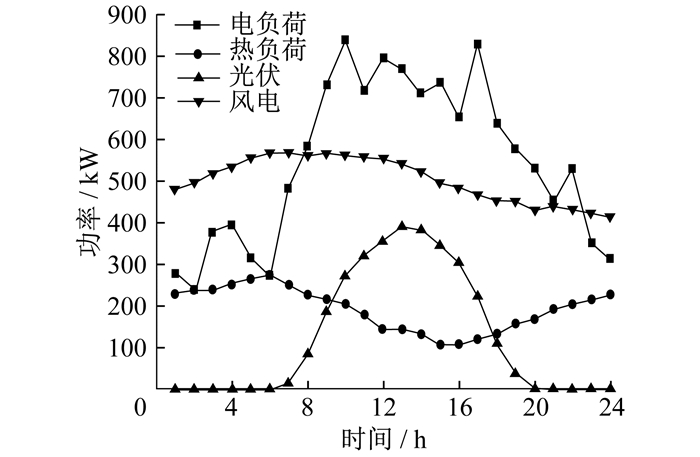
本文以某配电网实际数据为算例, 调度周期为24 h, 步长为1 h。风光、负荷和需求响应功率量预测曲线如图 4和图 5所示。样本数取500, 削减后场景数为5。通过MATLAB 2018a和Gurobi商业求解器进行求解。
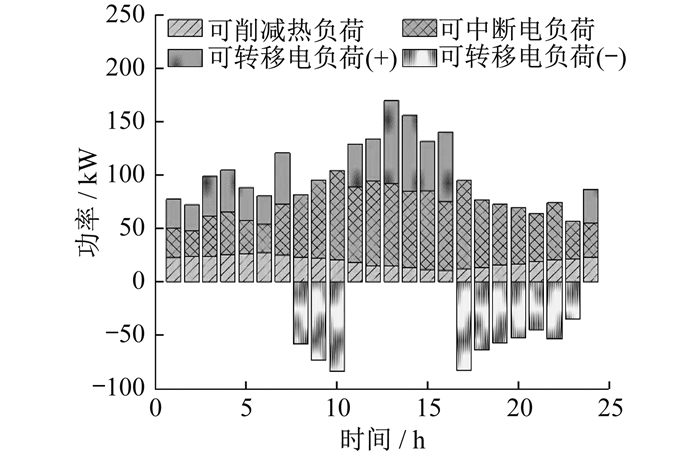
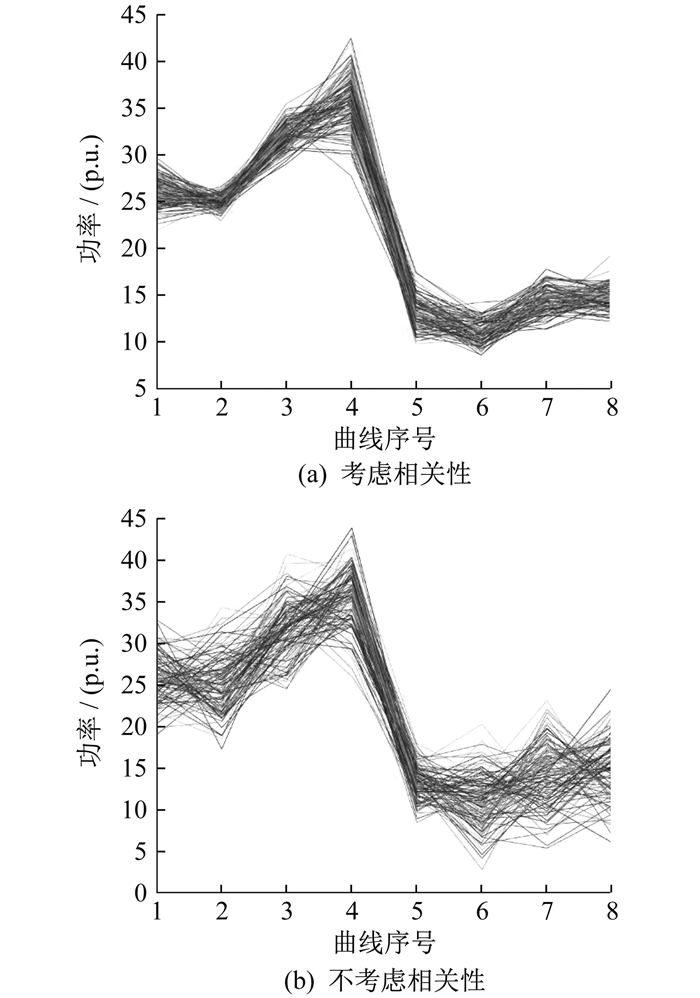
利用拉丁超立方采样, 得到考虑相关性和不考虑相关性两种情况下的100个场景。这里需求响应资源只选取可中断电负荷和可削减热负荷进行分析, 具体如图 6所示。
其中, 曲线序号1、2为风电出力, 曲线序号3、4为光伏出力, 曲线序号5、6为可中断电负荷功率, 曲线序号7、8为可削减热负荷功率。将风电功率减小至1/20, 光伏功率减小至1/10, 可中断电负荷功率减小至1/5。由图 6(a)可以发现, 当考虑相关性时, 风光与需求响应功率之间正相关性, 线条平滑且大部分接近平行; 由图 6(b)可知, 在不考虑相关性的情况下, 线条分布更加随机和无序。
5.2 IES运行结果及灵活性分析
本文设置3种调度方案: 方案1为用户不参与需求响应、不计及灵活性需求偏差; 方案2为用户参与需求响应、不计及灵活性需求偏差; 方案3为用户参与需求响应、计及灵活性需求偏差。
对上述3种调度方案的运行成本进行分析, 结果如表 1所示。
表 1
3种方案的运行成本
| 方案 | 成本类型 | |||
| 燃气轮机成本 | 储能设备与购能成本 | 需求响应成本 | 总运行成本 | |
| 1 | 16 731.3 | 1 226.4 | 0 | 17 957.7 |
| 2 | 15 020.9 | 955.3 | 1 450 | 17 426.2 |
| 3 | 14 551.3 | 910.7 | 1 557 | 17 019.0 |
由表 1可知, 相比于方案1, 方案2虽多支出1 450元的需求响应调度费用, 但是其余成本有所下降。这是由于利用供需灵活性减少峰谷差, 从而降低了其他设备的调节成本。方案3比方案2多考虑了灵活性需求平衡, 除了需求响应成本有所增加, 其他成本都有减小, 这是由于考虑风光波动, 使新能源更加容易消纳, 从而减小了系统的灵活性调整费用。总运行成本上, 方案2比方案3高出407.2元, 进一步体现了计及灵活性需求偏差的方案3对于IES经济性的提升作用。
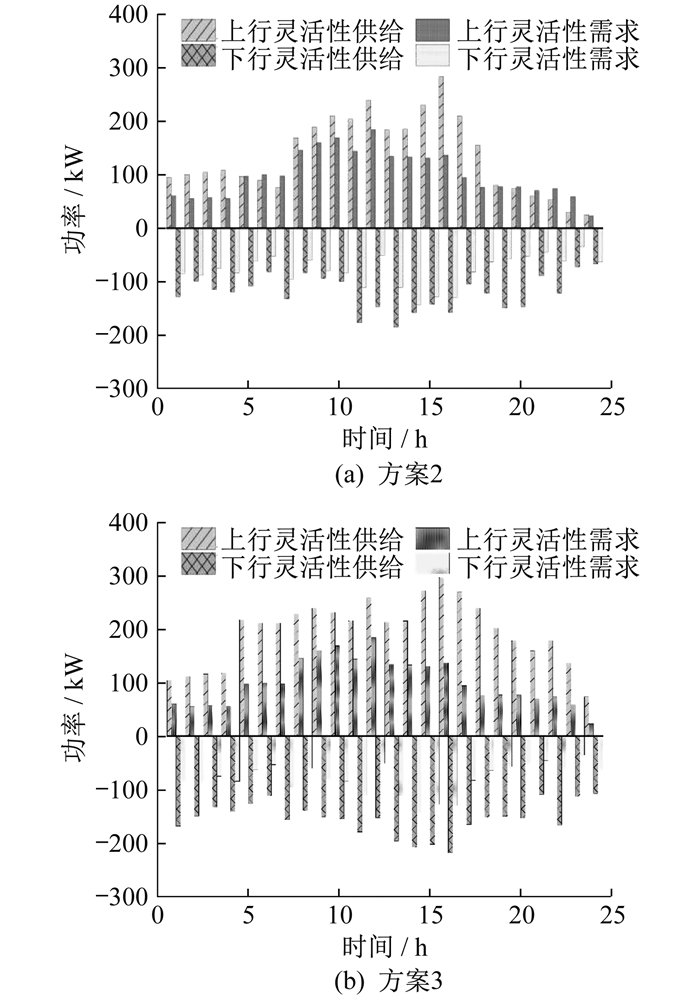
为了研究灵活性需求偏差对IES灵活性的影响, 对方案2和方案3的IES灵活性供需进行分析, 具体如图 7所示。
由图 7(a)可知, 方案2可以满足大部分时段的灵活性需求, 这是因为需求响应的削峰填谷效果给系统提供了一定的灵活性。但在6:00—7:00和20:00—23:00时段出现了灵活性供不应求的现象, 原因在于方案2并未考虑分布式电源出力波动和需求响应造成的需求偏差, 故灵活性设备未能在系统灵活性向上爬坡时提供额外贡献。从图 7(b)可以发现, 方案3的灵活性供给在各个时段均满足灵活性需求, 并且留有一部分余量。因相较于方案2, 方案3的灵活性供给因为日内阶段调度考虑了灵活性需求偏差, 故相邻时段的灵活性爬坡更加平缓, 爬坡功率量更加均衡地分配到每个调度时间段, 对IES灵活性有较大的提升。
5.3 需求响应对IES灵活性的影响
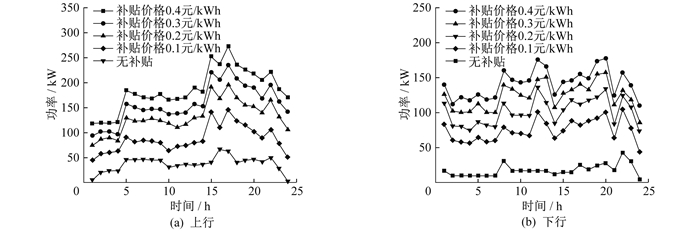
由于需求响应补贴价格会对负荷响应比例产生影响, 响应比例会令系统内的灵活性产生变化。为帮助综合能源运营商确立合适的补贴价格, 本文分析了不同补贴价格程度下IES灵活性余量, 结果如图 8所示。
由图 8可以看出, 在不实行用户补贴策略时, 微型燃气轮机和储能设备可以为系统提供必要的灵活性, 但由于IES负荷量波动较小, 常规负荷功率也较小, 因此系统上行与下行灵活性始终大于零。用户侧响应资源内调节负荷的占比跟随补贴价格逐步提高, 系统灵活性也得到提升。值得注意的是, 当补贴价格为0.4元/kWh, 系统上行和下行灵活性余量整体上提升最大。这表明设定合理的补贴价格能够为IES灵活性提升做出贡献。
5.4 DRO模型保守性分析
将不确定性置信水平α1和α∞分别等于0.5和0.99, 分析不同历史数据样本数和削减的典型场景数对DRO模型保守性的影响程度。
表 2为不同数据的历史样本数对模型保守性的影响。
表 2
历史样本数分析
| 样本数 | 运行成本/元 | 总运行成本/元 | 灵活性需求偏差/kW | ||||
| 燃气轮机 | 储能设备与购能 | 可转移电负荷 | 可中断电负荷 | 可削减热负荷 | |||
| 500 | 14 551.3 | 910.7 | 550 | 677 | 330 | 17 019.0 | 49.2 |
| 1 000 | 14 250.9 | 843.5 | 539 | 639 | 302 | 16 574.4 | 45.8 |
| 2 000 | 14 199.2 | 843.5 | 511 | 614 | 287 | 16 454.7 | 41.3 |
| 5 000 | 14 115.8 | 841.0 | 505 | 601 | 283 | 16 345.8 | 41.3 |
由表 2可以看出, 随着样本数不断增加, IES内设备运行成本和IES灵活性需求偏差都在减少。这是因为历史数据样本数量越大, 其概率分布允许偏差值α1和α∞缩小, 能够提升DRO模型的保守程度。
表 3为削减后的典型场景数目对模型保守性的影响。
表 3
典型场景数目分析
| 场景数 | 运行成本/元 | 总运行成本/元 | 灵活性需求偏差/kW | ||||
| 燃气轮机 | 储能设备与购能 | 可转移电负荷 | 可中断电负荷 | 可削减热负荷 | |||
| 5 | 14 551.3 | 910.7 | 550.0 | 677 | 330 | 17 019.0 | 49.2 |
| 10 | 14 570.4 | 913.5 | 553.1 | 679 | 332 | 17 048.0 | 49.3 |
| 15 | 14 606.7 | 914.4 | 514.5 | 680 | 336 | 17 051.6 | 52.9 |
| 20 | 14 613.5 | 917.3 | 519.0 | 684 | 340 | 17 073.8 | 73.2 |
由表 3可知, 随着场景数目增多, 模型保守程度也在增加。这是由于随着削减典型场景数增多, 削减后场景分辨率增大, 提升了原本在众多样本数据中的极端恶劣场景数据成为典型场景的概率。总之, 典型场景更能反映风光负荷的真实波动变化, 显著提升模型的鲁棒性。
5.5 同其他优化方法的对比分析
为验证本文方法在较大规模系统中的适用性和可行性, 将本文所提出的DRO模型与传统两阶段鲁棒优化模型(RO)、随机优化模型(SO)进行对比分析。文中所提出的DRO模型的样本数M取500, 削减场景数K为5, 不确定性置信水平α1和α∞分别取0.5和0.99。上述3种模型的优化结果如表 4所示。
表 4
不同模型优化结果比较
| 模型 | 发电侧各设备运行成本/元 | 用户侧响应资源运行成本/元 | 灵活性需求偏差/kW | 计算时间/s |
| DRO | 15 862.0 | 1 557.0 | 49.2 | 3.71 |
| RO | 20 416.9 | 1 599.4 | 54.2 | 8.45 |
| SO | 15 459.4 | 1 513.2 | 45.3 | 3.69 |
由表 4可知, 3种模型的发电侧各设备运行成本相差较大, 用户侧响应资源成本相差较小。RO模型得出的优化结果中各部分费用和灵活性需求偏差最大, 这是由于RO模型考虑了较多的最恶劣场景, 保守程度更大。本文提出的DRO模型总运行成本明显高于SO模型, 这是由于该模型调用了更多的供能侧和用户侧资源来消纳新能源和需求响应的不确定性。总之, 本文所提的DRO模型结合了RO模型和SO模型两者的优越性, 概率分布通过综合范数模糊集构建, 在一定保守性的基础上更加接近实际场景, 同时保证了灵活性和经济性。同时, 与RO模型相比, 本文所提DRO模型的计算时间明显低于RO模型, 这是由于在处理子问题时不需要做对偶处理, 从而大幅提升了模型的计算效率。
为进一步体现所提模型的优越性, 将DRO模型与SO模型在总运行成本和灵活性需求偏差进行比较, 结果如表 5所示。
表 5
两种模型总运行成本和灵活性需求偏差对比
| M | DRO | SO | |||
| 总运行成本/元 | 灵活性需求偏差/kW | 总运行成本/元 | 灵活性需求偏差/kW | ||
| 500 | 1 7419.0 | 49.2 | 16 882.8 | 44.9 | |
| 1 000 | 16 974.4 | 41.3 | 16 345.8 | 41.3 | |
| 2 000 | 16 654.7 | 41.3 | 16 345.8 | 41.3 | |
| 5 000 | 16 345.8 | 41.3 | 16 345.8 | 41.3 | |
由表 5可知, 本文所提DRO模型的灵活性需求偏差和总运行成本始终大于SO模型, 是由于SO模型并未考虑产生最恶劣场景的概率分布, 保守性较低。但随着历史数据样本数增加, DRO模型与SO模型的运行结果趋于同一, 表明DRO模型应对风险的调节能力很强, 拥有较好的风险调节能力。
6 结论
(1) 在灵活性供需平衡中计及灵活性需求偏差后, 可以显著提升IES的运行灵活性和经济性, 并且上行和下行灵活性余量随着需求响应的补贴价格增加而增加。
(2) DRO模型充分考虑了DG和需求响应的不确定性。当历史数据样本个数或典型场景数目越多, 方案的经济性越好, 保守程度越高。
(3) DRO模型可以改善鲁棒优化和随机优化的局限性和片面性, 在一定程度上实现了经济性、鲁棒性和灵活性3方面的均衡。
参考文献
-
[1]刘玉洁, 袁旭峰, 邹晓松, 等. 基于柔性多状态开关的分布式电源消纳技术评述[J]. 电测与仪表, 2022, 59(7): 1-8.
-
[2]SADEK S M, OMARAN W A, HASSAN M A M, et al. Data driven stochastic energy management for isolated microgrids based on generative adversarial networks considering reactive power capabilities of distributed energy resources and reactive power costs[J]. IEEE Access, 2021, 9(1): 5397-5411.
-
[3]王会超, 秦昊, 周昶, 等. 计及新能源预测不确定性的跨区域日前-日内调度模型[J]. 电力系统自动化, 2019, 43(19): 60-72.
-
[4]GUO Z J, WEI W, CHEN L J, et al. Distribution system operation with renewables and energy storage: a linear programming based multistage robust feasibility approach[J]. IEEE Transactions on Power Systems, 2022, 37(1): 738-749. DOI:10.1109/TPWRS.2021.3095281
-
[5]董燕, 杨俊林, 朱永胜, 等. 基于零和博弈的电力系统鲁棒优化调度研究[J]. 电力系统保护与控制, 2022, 50(5): 55-64.
-
[6]张亚超, 黄张浩, 郑峰, 等. 基于风电出力模糊集的电-气耦合系统分布鲁棒优化调度[J]. 电力系统自动化, 2020, 44(4): 44-55.
-
[7]DING T, YANG Q R, YANG Y H, et al. A data-driven stochastic reactive power optimization considering uncertainties in active distribution networks and decomposition method[J]. IEEE Transactions on Smart Grid, 2018, 9(5): 4994-5004. DOI:10.1109/TSG.2017.2677481
-
[8]BAGHERI A, WANG J H, ZHAO C Y. Data-driven stochastic transmission expansion planning[J]. IEEE Transactions on Power Systems, 2017, 32(5): 3461-3470. DOI:10.1109/TPWRS.2016.2635098
-
[9]郑晓东, 陈皓勇, 段声志, 等. 基于场景概率驱动的输电网和储能分布鲁棒规划[J]. 电力自动化设备, 2022, 42(6): 170-178.
-
[10]ZHAO C Y, GUAN Y P. Data-driven stochastic unit commitment for integrating wind generation[J]. IEEE Transactions on Power Systems, 2016, 31(4): 2587-2596.
-
[11]CAO Y W, WANG L Y, JIANG S G, et al. Optimal operation of cold-heat-electricity multi-energy collaborative system based on price demand response[J]. Global Energy Interconnection, 2020, 3(5): 430-441.
-
[12]BEIRON J, MONTANES R M, NORMANN F, et al. Combined heat and power operational modes for increased product flexibility in a waste incineration plant[J]. Energy, 2020, 202(1): 117696.
-
[13]王子驰, 雷炳银, 杨灵艺, 等. 考虑电热联合需求响应的区域综合能源系统多目标双层优化调度[J]. 电力系统及其自动化学报, 2021, 33(7): 120-127.
-
[14]孙毅, 胡亚杰, 郑顺林, 等. 考虑用户响应特性的综合需求响应优化激励策略[J]. 中国电机工程学报, 2022, 42(4): 1402-1413.
-
[15]李宁, 孙文慧, 毕云帆, 等. 考虑需求响应不确定性的综合能源系统优化调度研究[J]. 电气工程学报, 2023(1): 153-159.
-
[16]李慧斌, 刘翔宇, 顾雪平, 等. 考虑区域间灵活性资源互济的日前分散协调调度策略[EB/OL]. (2023-02-16)[2023-05-04]. http://h-p.kns.cnki.net.shiep.vpn358.com/kcms/detail/23.1202.TH.20230215.1334.010.html.
-
[17]苏承国, 申建建, 王沛霖, 等. 基于电源灵活性裕度的含风电电力系统多源协调调度方法[J]. 电力系统自动化, 2018, 42(17): 111-119.
-
[18]吉兴全, 刘健, 张玉敏, 等. 计及运行灵活性约束的综合能源系统优化调度[J]. 电力系统自动化, 2022, 46(16): 84-94.
-
[19]王强钢, 吴雪翚, 杨龙杰, 等. 考虑设备变工况特性和灵活性供需匹配的园区综合能源系统优化配置模型[J]. 电力自动化设备, 2023, 43(3): 20-28.
-
[20]税月, 刘俊勇, 高红均, 等. 考虑风电不确定性的电热综合系统分布鲁棒协调优化调度模型[J]. 中国电机工程学报, 2018, 38(24): 7235-7247.
-
[21]高海淑, 张玉敏, 吉兴全, 等. 基于场景聚类的主动配电网分布鲁棒综合优化[J]. 电力系统自动化, 2020, 44(21): 32-41.
-
[22]马浩天, 胡俊杰, 童宇轩. 考虑灵活性的数据中心微网两阶段鲁棒规划方法[EB/OL]. (2022-08-25)[2023-05-04]. http://h-p.kns.cnki.net.shiep.vpn358.com/kcms/detail/11.2107.TM.20220824.1748.027.html.
-
[23]贺帅佳, 高红均, 刘俊勇, 等. 计及需求响应柔性调节的分布鲁棒DG优化配置[J]. 中国电机工程学报, 2019, 39(8): 2253-2264.
-
[24]侯健敏, 余威杰, 徐志豪, 等. 考虑柔性电/热负荷的综合能源系统分布鲁棒优化调度[EB/OL]. (2021-10-20)[2023-05-04]. http://h-p.kns.cnki.net.shiep.vpn358.com/kcms/detail/23.1202.TH.20211019.1225.004.html.