随着“双碳”目标的推进, 电力电子装备已成为电力系统的重要组成部分, 其中逆变器扮演着重要角色。因此, 为了解决逆变器无惯性、欠阻尼不足等问题, 通过借鉴同步发电机的物理机理, 能够模拟同步发电机惯量和阻尼特性的虚拟同步发电机(Virtual Synchronous Generator, VSG)技术应运而生^[1-3]。

基于电力电子设备的特性, VSG可以灵活调节其惯量和阻尼系数。当然, 合适的控制参数能够优化系统动态调节能力, 但若参数取值不当, 则可能引起系统功率振荡, 降低系统稳定性^[4]。针对VSG参数的控制策略, 文献[4]引入模糊算法, 使得转动惯量在调节时更为平滑, 但模糊算法中的模糊规则和隶属度函数过于依赖研究人员的经验。文献[5]结合转动惯量自适应控制方法, 基于频率变化量改变转动惯量的取值, 从而提高了系统的稳定性, 但忽略了阻尼的影响。文献[6]考虑了阻尼参数对系统稳定性的影响, 提出了惯量和阻尼的协同控制策略, 但只能分段而不能连续自适应地改变参数。文献[7-10]通过引入定系数实现惯量阻尼双参数随频率变化情况自适应调整, 且运行可靠, 但调节效果取决于相关定系数的取值。文献[11]利用神经网络算法处理连续非线性函数的优势, 将神经网络输出作为VSG的转动惯量, 虽然能够快速响应系统频率变化, 缓冲系统受到的扰动, 但阻尼参数为定值。

VSG控制的本质是将储能单元中的电势能模拟成为具有惯性的机械能, 因此VSG的惯量和阻尼与储能荷电状态(State of Charge, SOC)密切相关。然而当前研究大多将VSG直流侧简化成理想电源。文献[12]通过惯量阻尼参数的变化动态配置储能单元, 并借助线性优化控制降低能量成本, 抑制功率波动。文献[13-14]提出了系统的等效惯量计算方法, 但该方法未考虑SOC对等效惯量计算的约束。文献[15]计算得到考虑储能SOC约束下的VSG惯量阻尼边界, 但无法实现VSG控制系数自动调节。

本文基于维持储能SOC水平的角度, 同时考虑VSG参数与频率的非线性关系, 设计基于SOC的储能充放电系数, 并结合径向基函数(Radial Basis Function, RBF)神经网络控制提出了一种储能VSG参数自适应控制策略。最后基于MATLAB/Simulink搭建仿真模型, 并在阶跃负荷扰动工况下, 验证了本文所提策略的有效性。

基于LC滤波的VSG电路拓扑结构如图 1所示^[16]。其中, 储能通过电力电子器件与配电网相连, 并网逆变器采用VSG控制策略。VSG可根据系统频率变化调整储能充放电功率, 以支撑系统频率稳定; 三相桥臂中点电压e_a、e_b和e_c等效同步发电机的电势E; 滤波器的电感L₁和电阻r₁等效同步发电机的电感L_d和定子电阻r_a; 滤波电容电压u_a、u_b、u_c等效同步发电机的端电压U_g。PCC为公共耦合点, i_a、i_b和i_c是逆变器输出电流, C是滤波电容, r_g、L_g是线路电阻、电感, δ是VSG的虚拟功角, Z是VSG与电网间的等效阻抗。

根据同步发电机的二阶模型得到VSG的转子运动方程为(令VSG极对数为1)

$ \left\{\begin{array}{l} \Delta \omega_{*}=\frac{\omega-\omega_{0}}{\omega_{0}} \\ \frac{\mathrm{d} \delta}{\mathrm{d} t}=\Delta \omega_{*} \omega_{0} \\ H \frac{\mathrm{d} \omega_{*}}{\mathrm{~d} t}=P_{\mathrm{m} *}-P_{\mathrm{e} *}-P_{\mathrm{D} *} \\ P_{\mathrm{D} *}=D \Delta \omega_{*} \end{array}\right. $

(1)

式中: Δω_*——VSG频率偏差标幺值;

ω——VSG输出角频率;

ω₀——额定角频率;

H——VSG惯性时间常数;

P_m*、P_e*、P_D*——VSG的输入机械功率标幺值、电磁功率标幺值和阻尼功率标幺值;

D——阻尼系数。

H的表达式为

$ H=J \frac{\omega_{0}^{2}}{S_{\mathrm{N}}} $

(2)

式中: J——VSG转动惯量;

S_N——VSG额定容量。

由图 1可得VSG的电磁方程为

$ L \frac{\mathrm{d} i_{\mathrm{abc}}}{\mathrm{d} t}=e_{\mathrm{abc}}-U_{g}-R i_{\mathrm{abc}} $

(3)

式中: i_abc——逆变器输出电流;

e_abc——VSG虚拟内电势瞬时值;

R——电阻。

e_abc的计算公式为

$ e_{\mathrm{abc}}=\left[\begin{array}{c} e_{\mathrm{a}} \\ e_{\mathrm{b}} \\ e_{\mathrm{c}} \end{array}\right]=\left[\begin{array}{c} E \sin \delta \\ E \sin \left(\delta-\frac{2 {\rm{\pi}}}{3}\right) \\ E \sin \left(\delta+\frac{2 {\rm{\pi}}}{3}\right) \end{array}\right] $

(4)

其中, VSG虚拟内电势指令值E可由无功功率偏差经积分得到, 为

$ \begin{aligned} & E=U_{\mathrm{n}}\left\{E_{0 *}+\right. \\ & \left.K \int\left[Q_{\mathrm{ref} *}-K_{\mathrm{v}}\left(U_{*}-U_{\mathrm{g} *}\right)-Q_{\mathrm{e} *}\right] \mathrm{d} t\right\} \end{aligned} $

(5)

式中: U_n——电压基准值;

E_0*——空载电势;

K——无功功率积分系数;

Q_ref*、Q_e*——VSG输出无功功率参考值和实际值;

K_v——电压调差系数;

U_*——滤波电容电压;

U_g*——电网电压。

K_v的计算方法为

$ K_{\mathrm{v}}=\frac{\Delta Q_{*}}{\Delta U_{*}} $

(6)

式中: ΔQ_*——VSG输出无功功率变化量标幺值;

ΔU_*——并网点电压幅值变化量标幺值。

通常阻抗Z的阻抗角可近似为零, 同时δ很小, sinδ≈δ, 故储能VSG输出有功功率为

$ \begin{gathered} P_{\mathrm{e} *}=\frac{E_{*} U_{*}}{Z_{*}} \sin \delta=S_{\mathrm{E}} \delta \\ S_{\mathrm{E}}=\frac{E_{*} U_{*}}{Z_{*}} \end{gathered} $

(7)

式中: E_*——VSG内电势标幺值;

Z_*——VSG与电网间等效阻抗标幺值;

S_E——VSG整步功率系数。

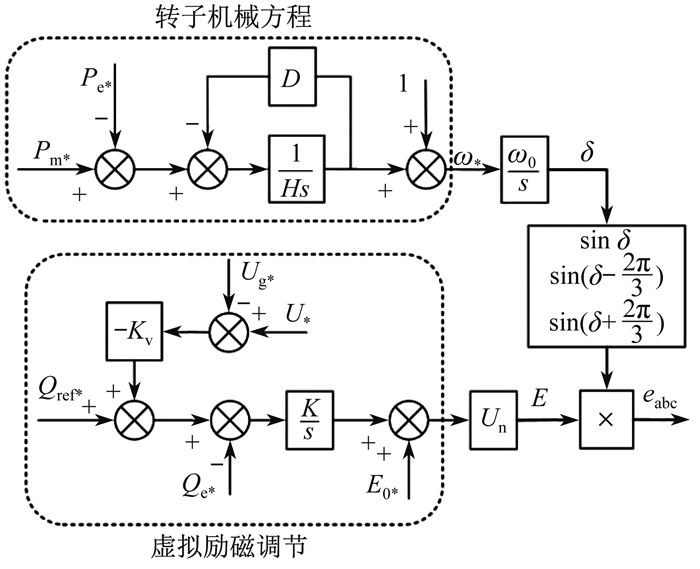
VSG控制框图如图 2所示。其中, s为微分算子。

由图 2可知, VSG有功功率-频率下垂特性可表示为

$ D=\frac{\Delta P_{*}}{\Delta \omega_{*}} $

(8)

式中: D——阻尼系数;

ΔP_*——VSG有功功率变化量。

当电网存在频率偏差时, 储能VSG参与电网调频的有功功率变化量ΔP_*与系统频率偏差标么值Δω_*成正比, 阻尼系数D越大, 储能参与电网一次调频的程度越深。

储能VSG为典型的二阶系统, 其有功功率-频率环闭环传递函数G_P(s)为

$ G_{\mathrm{P}}(s)=\frac{\Delta P_{\mathrm{e} *}}{\Delta P_{\mathrm{m} *}}=\frac{S_{\mathrm{E}} \omega_{0}}{H s^{2}+D s+S_{\mathrm{E}} \omega_{0}} $

(9)

式中: ΔP_e*——VSG输出功率变化量;

ΔP_m*——VSG输入机械功率变化量。

系统阻尼比ξ和自然角频率ω_n之间的关系为

$ \left\{\begin{array}{l} \omega_{\mathrm{n}}=\sqrt{\frac{S_{\mathrm{E}} \omega_{0}}{H}} \\ \xi=\frac{\frac{1}{2} D}{\sqrt{H S_{\mathrm{E}} \omega_{0}}} \end{array}\right. $

(10)

当VSG为欠阻尼系统时, VSG输出功率ΔP_e*的最大值为^[17]

$ \Delta P_{\mathrm{e} *}=\Delta P_{\mathrm{m} *}\left(1-\mathrm{e}^{-\frac{\xi \pi}{\sqrt{1-\xi^{2}}}}\right) $

(11)

锂电池能量密度高、功率密度高、循环寿命长, 本文的电池储能系统(Battery Energy Storage System, BESS)为典型的采用锂电池的电化学储能。锂电池的伏安特性与其端电压和内阻有关, 而其电压和内阻受SOC影响, BESS的剩余容量可由S_OC表示, 为

$ S_{\mathrm{oc}}=S_{\mathrm{oc}_{0}}-\frac{1}{Q_{\mathrm{n}}} \int P_{\mathrm{BESS}} \mathrm{d} t $

(12)

式中: S_oc0——BESS初始荷电状态;

Q_n——储能额定容量;

P_BESS——BESS充放电功率。

为避免锂电池过充和过放, 延长锂电池使用寿命, 提高BESS经济性, 应对BESS充电和放电工况下的SOC作出限制。当SOC低于下限值0.1时, BESS不应对外输出电能, 防止锂电池过放; 当SOC高于上限值0.9时, BESS不应再吸收电能, 防止锂电池过充。

为了保证BESS充电、放电能力的一致性, 系统运行前应使储能SOC处于预设值。其参考值S_ocref为

$ S_{\mathrm{oc}_{\mathrm{ref}}}=\frac{S_{\mathrm{oc}_{\text {max }}}+S_{\mathrm{oc}_{\text {min }}}}{2} $

(13)

式中: S_ocmax、S_ocmin——BESS荷电状态的上限和下限。

储能VSG通过模拟VSG的下垂特性和惯性响应, 参与系统一次调频。在调频过程中, 不考虑暂态过程, 储能VSG调频出力来源于VSG下垂特性, 即

$ \Delta P_{\mathrm{D} *}=-D \Delta \omega_{*} $

(14)

式中: ΔP_D*——储能VSG下垂功率。

基于系统频率变化量和VSG阻尼系数, 降低稳态频率偏移。

为了延长储能运行时间, 当电网频率低于工频时, 储能应在SOC较低时降低功率, SOC较高时增加功率; 当电网频率高于工频时, 储能应在SOC较低时增大充电功率, SOC较高时减小充电功率。设计基于SOC的储能充放电系数K_soc为

$ K_{\mathrm{soc}} = \begin{cases}K_{\mathrm{soc} \_ \text {dis }}, P_{\mathrm{e}}>0 \\ K_{\mathrm{soc} \_\mathrm{ch}}, P_{\mathrm{e}}<0\end{cases} $

(15)

$ K_{\mathrm{soc} \_ \text {dis }} = \begin{cases}2 S_{\mathrm{oc}}, \quad S_{\mathrm{oc}} \in[0, 0.5] \\ 1, \quad S_{\mathrm{oc}} \in[0.5, 1]\end{cases} \\ K_{\mathrm{soc} \_\mathrm{ch}} = \begin{cases}1, \quad S_{\mathrm{oc}} \in[0, 0.5] \\ 1-2\left(S_{\mathrm{oc}}-S_{\mathrm{oc_{ref}}}\right), \quad S_{\mathrm{oc}} \in[0.5, 1]\end{cases} $

(16)

式中: K_{soc_dis}、K_{soc_ch}——储能系统放电和充电状态下系数;

S_ocref——储能SOC参考值, 取0.5。

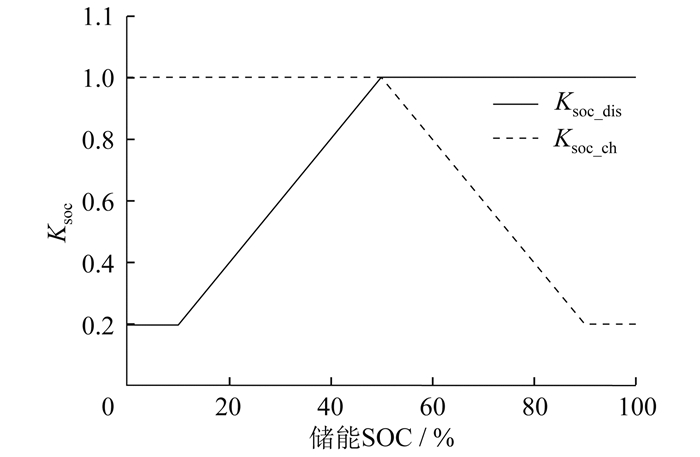
由式(15)、式(16)得到基于SOC的储能充放电系数曲线, 如图 3所示。

为了使储能VSG能够根据锂电池荷电状态自适应调整其一次调频功率, 延长储能系统运行时间, 避免锂电池过充或过放使VSG有功功率突然跌落, 进而导致电网频率振荡。设计基于储能充放电系数K_soc的VSG阻尼系数D为

$ D=K_{\mathrm{soc}} D^{\prime}, \quad K_{\mathrm{soc}} \geqslant 0.2 $

(17)

储能VSG在有功指令P_m*阶跃或受到负荷扰动过程中, 除了可以通过阻尼系数降低系统稳态频率偏差, 在暂态过程中还可基于H向电网提供惯性响应, 快速响应系统频率变化, 抑制系统频率的快速恶化。典型欠阻尼二阶系统调节时间t_s可表示为(误差带取±5%)

$ t_{\mathrm{s}}=\frac{3.5}{\xi \omega_{\mathrm{n}}}=\frac{7 H}{D} $

(18)

阻尼不变时, 惯性时间常数H与系统调节时间成正比, H越大, 频率恢复时间越长。因此, 有必要根据系统频率变化状况自适应调节VSG的惯性时间常数H, 从而改善储能VSG在受到频率扰动时的动态响应性能, 优化储能VSG的频率响应能力。

神经网络控制的自学习能力使得控制器不依赖于系统模型和参数信息, 可被广泛用于解决非线性时变问题。本文采用RBF神经网络设计自适应控制器, 根据电网频率变化情况动态改变储能VSG惯性时间常数, 无需掌握参数H对应的Δω_*与dω_*/dt的动态特性。基于RBF神经网络的惯性自适应模型结构简单, 且无冗长的计算。

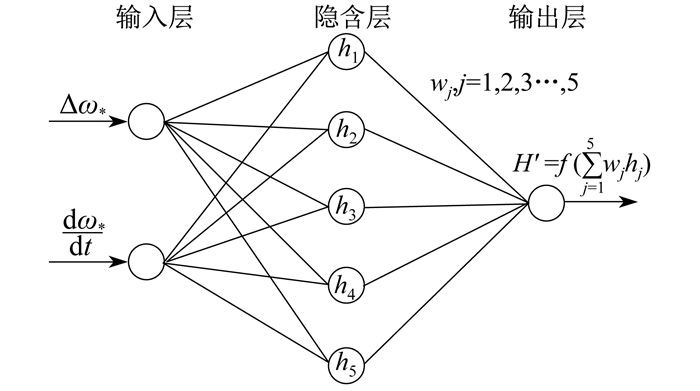
将频率变化量和频率变化率作为RBF网络的输入, 输出作为储能VSG的惯性时间常数, 设计RBF神经网络结构，如图 4所示。其中, h_j为第j个神经元的隐含层激活函数, w_j为第j个神经元的输出层权值, H′为RBF控制器输出值, f(x)为输出层激活函数。

神经网络隐含层的激活函数为高斯基函数h(x), 为

$ h(x)=\exp \left(\frac{-\left\|\boldsymbol{x}-c_{j}\right\|^{2}}{2 b_{j}^{2}}\right) $

(19)

式中: c_j、b_j——隐含层第j个神经元高斯基函数的中心和宽度。

采取Sigmoid函数作为神经网络输出层的激活函数, 为

$ f(x)=\frac{1}{1+\mathrm{e}^{-x}} $

(20)

神经网络的评价函数为

$ E(k)=\frac{1}{2}\left[\omega_{0 *}(k)-\omega_{*}(k)\right]^{2} $

(21)

式中: k——迭代次数。

根据梯度下降法, 神经网络权值的调整方式为

$ \Delta w_{j}(k)=-\eta \frac{\partial E(k)}{\partial w_{j}}+\alpha \Delta w_{j}(k-1) $

(22)

$ \frac{\partial E(k)}{\partial w_{j}}=\frac{\partial E(k)}{\partial \omega_{*}(k)} \cdot \frac{\partial \omega_{*}(k)}{\partial H(k)} \cdot \frac{\partial H(k)}{\partial \sum w_{j} h_{j}} \cdot \frac{\partial \sum w_{j} h_{j}}{\partial w_{j}} $

(23)

式中: η——学习率, η∈(0, 1);

α——惯性系数, α∈(0, 1)。

考虑到系统的Jacobian矩阵计算过于复杂, 本文用sign(Δω_*/ΔH)代替∂ω_*(k)/∂H(k)。进而得到RBF神经网络的权值调整公式为

$ \begin{aligned} \Delta w_{j}(k)= & \eta\left[\omega_{0 *}(k)-\omega_{*}(k)\right] \cdot \\ & \operatorname{sign}\left[\frac{\omega_{*}(k)-\omega_{*}(k-1)}{H(k)-H(k-1)}\right] \cdot \\ & \dot{f}\left[\sum\limits_{j=1}^{5} w_{j}(k) h_{j}(k)\right] \cdot \\ & h_{j}(k)+\alpha \Delta w_{j}(k-1) \end{aligned} $

(24)

式中: $\dot{f}$——函数f的一阶导数。

由式(1)可得:

$ \Delta \omega_{*}=\frac{P_{\mathrm{m} *}-P_{\mathrm{e} *}-H \cdot \frac{\mathrm{d} \omega_{*}}{\mathrm{~d} t}}{D} $

(25)

假设P_m*-P_e*-Hdω_*/dt不变, 则阻尼系数D越大, 系统频率偏差越小, 因此可在暂态过程中根据系统频率变化量调节VSG阻尼系数, 以降低VSG受到频率扰动时的频率过冲量Δω_*max。因此根据D对Δω_*的影响, 设计的阻尼参数调节策略为

$ D^{\prime}= \begin{cases}D_{0}, & \left|\Delta \omega_{*}\right| \leqslant T_{\mathrm{d}} \\ D_{0}+K_{\mathrm{d}}\left|\Delta \omega_{*}\right| \omega_{0}, & \left|\Delta \omega_{*}\right|>T_{\mathrm{d}}\end{cases} $

(26)

式中: D₀——下垂系数初值;

T_d——阈值;

K_d——阻尼系数D的调节系数。

综上所述, 本文设计的储能VSG参数自适应控制策略为

$ \begin{gathered} H=K_{\mathrm{soc}} H^{\prime} \\ D=K_{\mathrm{soc}} D^{\prime}=\left\{\begin{array}{l} K_{\mathrm{soc}} D_{0}, \quad\left|\Delta \omega_{*}\right| \leqslant T_{\mathrm{d}} \\ K_{\mathrm{soc}}\left(D_{0}+K_{\mathrm{d}}\left|\Delta \omega_{*}\right| \cdot \omega_{0}\right), \left|\Delta \omega_{*}\right|>T_{\mathrm{d}} \end{array}\right. \end{gathered} $

(27)

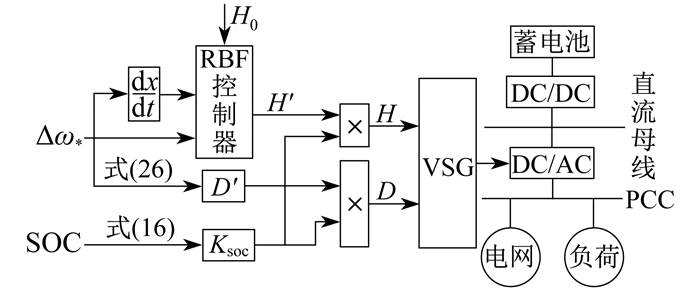
本文所提计及SOC储能VSG综合控制如图 5所示。

根据式(9)构建以H和D为参变量的特征方程为

$ \left\{\begin{array}{l} 1+\frac{D s}{H s^{2}+S_{\mathrm{E}} \omega_{0}}=0 \\ 1+\frac{\frac{1}{H}\left(D s+S_{\mathrm{E}} \omega_{0}\right)}{s^{2}}=0 \end{array}\right. $

(28)

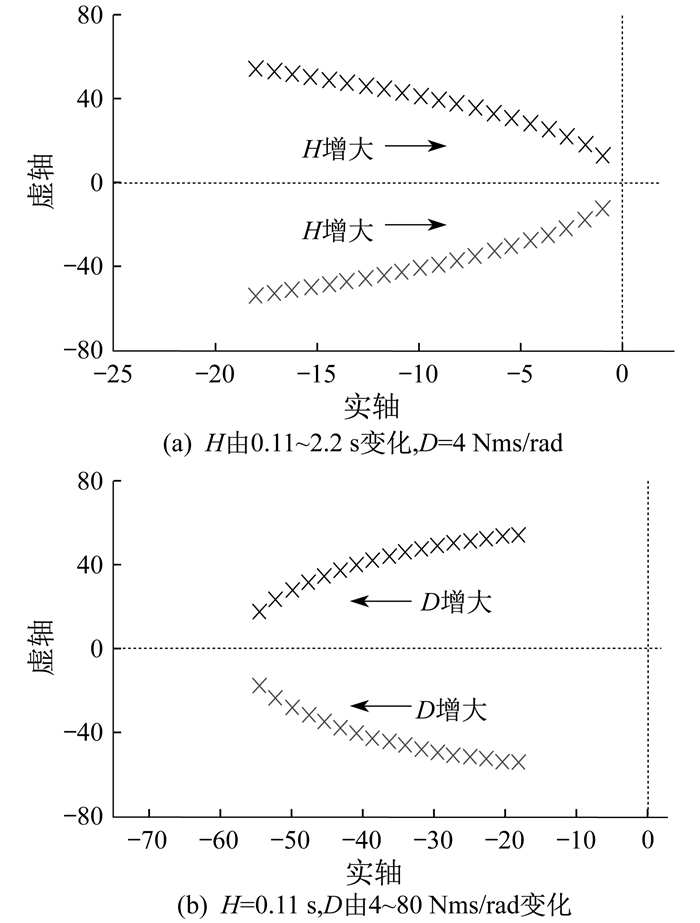
分别以H和D为参变量的广义根轨迹如图 6所示。

由图 6(a)可知, 当阻尼系数D不变时, 随着H的增大, 开环极点离虚轴越来越近, 系统稳定性越来越差, 因此参数H不能过大。由图 6(b)可知, 当H不变时, 阻尼系数D越大, 开环极点实部的绝对值就越大, 系统就越稳定, 系统响应速度也随之加快, 同时随着D增大, 系统阻尼比也增大, 系统超调量随之降低。

为满足系统稳定性要求, 应有D>0。同时阻尼系数D还需满足^[18]

$ D \leqslant \frac{\Delta P_{* \max }}{\Delta \omega_{* \max }} $

(29)

式中: ΔP_*max——VSG有功功率变化最大值;

Δω_*max——VSG角频率变化最大值。

本文设计下垂系数初值D₀=20, 令系统阻尼比为0.707, 此时参数H的初值H₀为0.55。当储能SOC达到上下限时, 由式(17)可得K_soc=0.2, 此时H和D有最小值H_min=0.11, D_min=4。结合式(18)、式(27)可知, 本文所提VSG控制策略中系统调节时间不受储能SOC影响。

通过MATLAB/Simulink平台验证本文所提的储能VSG自适应控制策略。其中, 蓄电池容量为3 A·h, 直流母线电压U_dc=800 V, r₁=0.1 Ω, L₁= 2 mH, L_v=2 mH, C=30 μF, 同步角频率ω₀=100 π rad/s, 电压基准值U_n=380 V, K_v=12.5, K=0.05。S_oc初始值设为0.5。系统初始带20 kW负荷, 分别对比本文所提策略与固定参数法(D₀=20, H₀=0.55)、常规自适应策略^[10]的频率稳定性和SOC维持效果。

考虑储能VSG参与系统一次调频的情况, 当电网频率下降0.5 Hz时, 本文的储能SOC曲线, 如图 7所示。

由图 7可知, 相比于固定参数控制, 本文所提控制策略能够有效维持储能SOC。

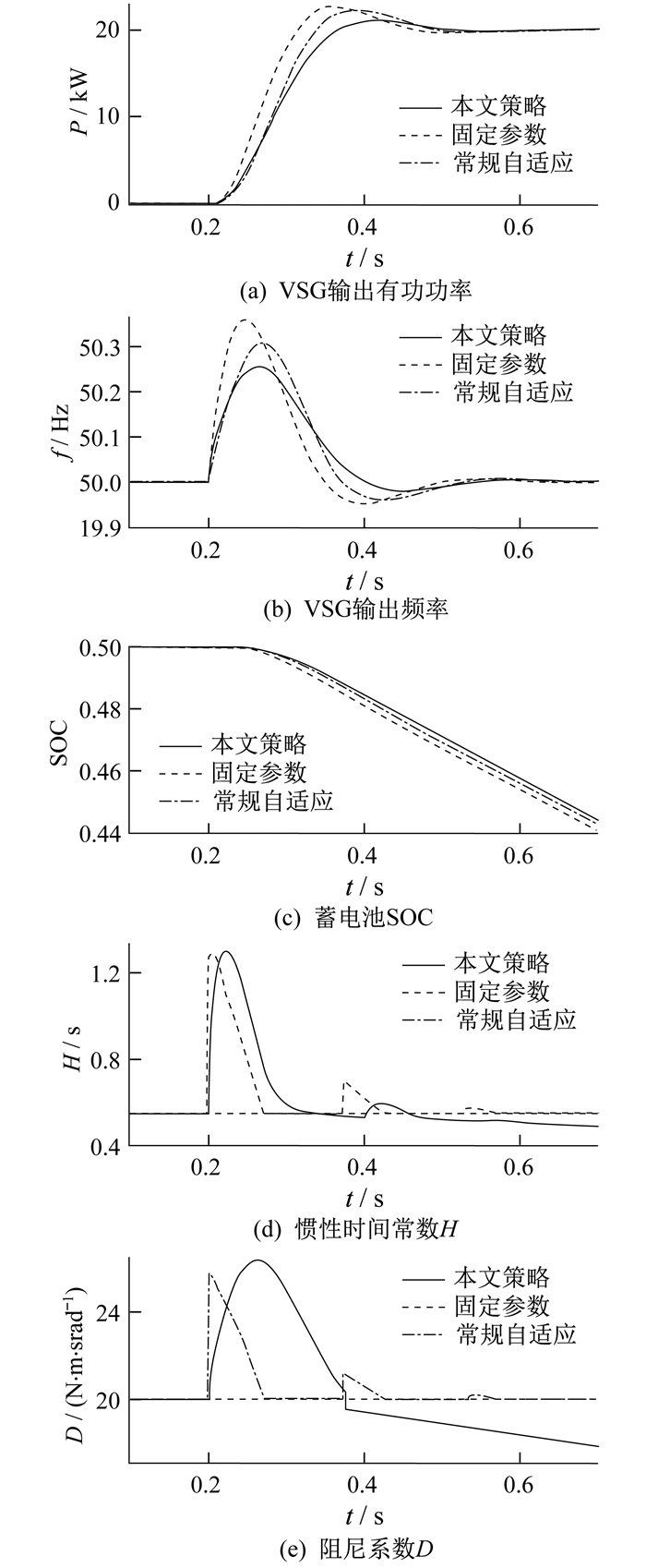
设定在0.2 s时刻VSG有功指令P_m突增20 kW, 3种VSG控制方式下储能逆变器输出有功功率、频率、蓄电池SOC和VSG的惯性阻尼自适应变化曲线如图 8所示。

由图 8可知, 采用固定参数控制时, 储能逆变器输出有功功率和频率的超调量较大, 调节时间较长; 与固定参数控制相比, 常规自适应控制下VSG参数H和D根据系统频率变化自适应调节, 明显减少了逆变器输出功率和频率的超调量; 与常规自适应控制相比, 本文所提策略控制下的有功超调量和最大频率偏差进一步减少, 频率恢复速度加快, 对蓄电池SOC的维持效果最好, 并且本文策略下的参数不存在突变, 参数变化较为缓和。

本文借助RBF神经网络对任意非线性函数的逼近能力, 无需分析VSG参数与逆变器输出频率变化情况之间复杂的非线性关系, 提出了考虑储能SOC的RBF自适应VSG控制策略, 得出如下结论。

(1) 储能参与电网调频时, 相比于固定参数, 本文所提策略可有效维持储能SOC水平, 避免储能过充、过放, 延长储能工作时间。

(2) 根据根轨迹分析基于VSG的储能系统的稳定性, 提高了参数选取的准确性。

(3) 采用本文所提控制策略, 能够有效改善储能逆变器输出功率和频率的动态特性, 提高系统稳定性, 且参数调节不存在突变。