|
|
|
发布时间: 2023-10-28 |
新型电力系统 |
|
|
|
收稿日期: 2023-06-01
基金项目: 国家自然科学基金(U2066214)
中图法分类号: TM9
文献标识码: A
文章编号: 2096-8299(2023)05-0443-10
|
摘要
针对电力市场环境下风光储参与日前电力市场方式的问题, 结合风光储互补特性和风光出力不确定特征, 对风光储独立和联合参与现货市场交易优化进行了比较研究。首先, 结合日前现货市场机制构建了风光储独立和联合参与市场的交易模式和基本框架。其次, 通过拉丁超立方采样和同步回代将风光出力随机变化过程转化为多个确定性概率场景。然后, 分别以预期收益最大为目标, 考虑合作的参与和激励约束, 建立了风光储独立和联合参与现货市场交易的优化模型, 并在此基础上进一步构建了考虑条件风险价值的联合交易优化模型。最后, 通过算例验证发现: 储能在独立和联合模式下均有平抑风光偏差的作用, 且后者效果更好; 同时, 联合模式下收益与风险水平呈现非严格的正相关关系, 实际应用中应设置适当的置信水平以获得更大利润。
关键词
风光储; 日前电力现货市场; 交易优化; 条件风险价值
Abstract
A comparative study is conducted on the optimization of independent and joint participation of wind and solar energy storage in spot electric energy market transactions, taking into account the complementary characteristics of wind and solar energy storage and the uncertain characteristics of wind and solar output, in response to the issue of market participation in the electricity market environment.First of all, combined with the centralized spot market, the transaction mode and basic framework of independent participation market and joint participation market of wind and solar storage are constructed; Secondly, the random variation process of wind and solar output is transformed into multiple deterministic probability scenarios through Latin hypercube sampling and synchronous backpropagation; Then, taking the maximum expected return as the goal, considering the participation and incentive constraints of cooperation, an optimization model of independent and joint participation of wind and solar energy storage in spot market transactions is established.On this basis, an optimization model of joint transactions considering conditional value at risk (CVaR) is further constructed.Finally, an example is designed to verify that the wind and solar energy storage plays a better role in stabilizing wind and solar deviation under independent and joint modes, and the latter has better effect.At the same time, there is a non strict positive correlation between returns and risk levels in the joint model, and in practice, appropriate confidence levels should be set to achieve greater profits.
Key words
wind-photovoltaic-storage; day-ahead electric spot market; conditional value at risk; optimizing operation
随着以风、光为代表的新能源的快速发展和电力市场化改革的深入,风力发电和光伏发电企业逐渐作为新的市场主体参与日前电力现货市场(以下简称“市场”)。在此背景下,研究风电、光伏在现货市场中的交易策略问题。一方面可以促进风光的消纳,另一方面可以提高风电和光伏发电企业在市场中的竞争力[1]。然而,风光新能源的出力随机性和不确定性会给其带来收益风险的同时,也会对市场安全平稳运行带来一定的风险[2]。随着储能技术的发展,灵活的充放电储能系统拥有峰值调节能力和足够的储备容量,成为一种降低可再生能源发电不确定性的重要手段,并提高了可再生能源参与市场的可控性[3]。
随着我国电力市场化改革的深入推进和风电-光伏发电-储能(以下简称“风光储”)成本的降低,三者将作为新的市场主体参与市场, 来获得市场化利益。文献[4]针对风储电站参与电力现货竞价问题, 考虑风电出力和现货价格的不确定性建立了两阶段优化方式,并采用混沌粒子群算法对所建模型进行求解。文献[5]将电池储能-抽水蓄能作为混合储能用来降低光伏波动对市场的影响, 以提高对光伏的接纳能力, 然后建立了日前-日内两阶段的“源-荷-储”协同优化调度策略。文献[6]根据分布式能源聚合商在日前市场和辅助服务市场的竞价行为建立了双层混合整数非线性规划模型,其中上下层均包含了离散和连续变量,并采用卡鲁什·库恩·塔克重构法将双层规划模型转化为单层优化模型。文献[7]考虑了风光机组和储能机组的约束条件,以利润最大化为目标,构建了风光储联合优化运行模型,研究了市场环境下风光储联合运行的发电计划安排。文献[8]研究了风光储混合发电商对市场均衡的影响, 结果表明, 风光储混合发电商参与市场可抑制传统发电商的市场力, 对市场出清价格有一定的调节作用。文献[9]考虑风光出力的波动性,设计了基于碳交易的现货市场机制,提出了风光储场站的报价策略, 以收益最大化为目标构建了报量报价的双层优化模型。
上述研究表明, 储能系统与风电、光伏合作对电力系统优化、提高预期效益有积极影响,但针对当前我国电力市场机制下储能系统和风光机组独立和联合交易,以及考虑风光出力不确定性风险的非中性决策的研究较少。
因此,本文对我国市场环境下风光储参与市场的交易模式进行了研究。首先, 从现货市场机制出发,分别针对风光储独立和联合参与市场的交易模式进行了分析, 并建立了框架。其次,采用拉丁超立方采样和同步回代的场景削减对风电和光伏出力不确定性进行处理,并建立了风光储独立和联合参与市场的优化模型, 以及考虑条件风险价值(Conditional Value at Risk, CVaR)下联合参与市场的优化模型,同时给出了约束条件。最后, 通过算例对两种模式下的风光储交易结果和收益情况进行分析,得出的结论是: 引入储能装置可以减少风电和光伏的偏差, 在联合模式下更有利于提升效益。
1 风光储参与市场的交易模式
1.1 日前现货市场机制
日前现货市场按照“全电量参与,风光优先”的原则, 采用分时电力竞争, 并通过集中优化计算进行出清, 形成分时节点价格。根据发改委2019年发布的《关于规范优先发电优先购电计划管理的通知》,风光机组执行优先发电计划, 在中长期市场签订政府授权差价合约后,在日前现货市场可采取报0价的方式参与市场保证优先出清, 即作为市场价格的接受者[10]。
日前现货市场的运行日为执行日前电力交易计划的自然日,每15 min或1 h为一个交易出清时段, 每个自然日划分为24或96个出清时段。日前市场竞价日为运行日的前一日, 由发电企业进行交易申报,并通过安全约束机组组合模型进行出清, 形成运行日的交易结果。日前市场采用节点边际电价定价机制,出清形成的每1 h的节点边际电价为该时段的市场出清价格。由于风光较强的不确定性和较差的可调度性, 因此其日前中标量和次日实际发电量往往存在偏差。对于正不平衡电量按弃电损失惩罚, 负不平衡电量按1.2倍的市场平均出清价格惩罚。
1.2 独立和联合交易模式
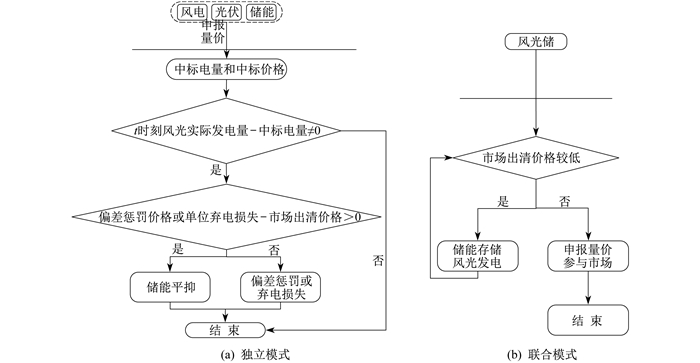
风电、光伏和储能作为新兴市场主体,通常可以采取独立或联合两种不同的模式参与日前现货市场。两种模式下参与市场交易的框架如图 1所示。
风光储独立参与模式下, 三者均以自身净收益最大化为目标。风电和光伏根据其出力预测参与日前市场投标; 储能则根据风光偏差惩罚价格(或单位弃电损失)是否小于市场出清价格来选择交易策略, 小于出清价格时直接参与市场, 反之则购售风光偏差电量。风光储联合参与模式下, 三者以联合体净收益最大化为目标。该模式具有可控性和可调性, 直接在市场进行策略性投标。当市场出清价格高时, 根据发电能力直接参与投标; 反之, 利用储能机组存储风光电量, 待市场出清价格高时再参与投标。
2 风光出力不确定性的场景技术
风电、光伏发电机组的功率输出具有不确定性,主要由风速和太阳辐射强度的随机特性引起,通常采用Weibull分布和Beta分布进行描述[11]。本文采用多场景技术(包括场景生成技术和场景削减技术)来处理风光机组功率不确定性问题, 并将其随机变化的过程转化为多个确定性概率场景。
2.1 场景生成技术
拉丁超立方采样(Latin Hypercube Sampling, LHS)属于分层抽样。相比于蒙特卡洛随机模拟抽样,LHS可以有效解决抽样样本聚集问题, 使得抽样样本更为全面地覆盖随机变量全部的样本空间, 因此也能更准确地反映随机变量的概率分布情况。以风速服从Weibull分布的风电为例, 基于LHS的随机变量抽样的过程步骤如下。
步骤1 确定要抽取的样本数A, 将随机变量风速vt的Weibull分布区间均分为A个子区间。
步骤2 对任意子区间[(i-1)/A, i/A], 从中随机抽取某个数yi, 且满足
| $ y_{i}=\frac{i-1+r}{A} $ | (1) |
式中: r——[0, 1]区间上服从均匀分布的随机变量。
步骤3 通过逆变换求取抽样样本值, 为
| $ v_{i, t}=F_{t}^{-1}\left(y_{i}\right) $ | (2) |
式中: vi, t——随机变量vt在第i个子区间的采样值;
Ft-1——累计概率分布函数Ft的反函数。
2.2 场景削减技术
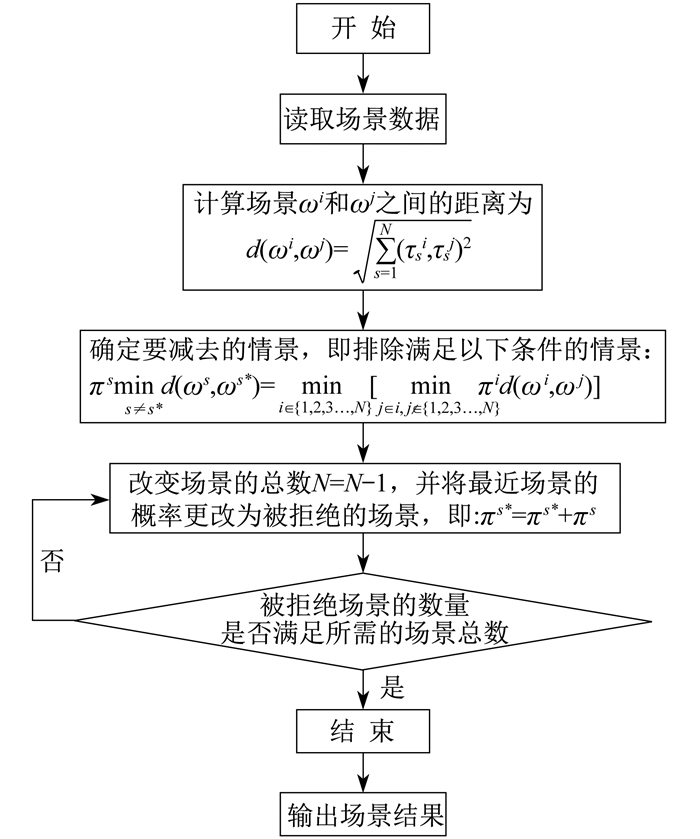
通过LHS得到的风电出力样本数量巨大,计算精度较高,但计算效率低下。为了兼顾样本的拟合精度和计算效率,本文采用同步回代法进行场景削减。场景削减流程如图 2所示。其中, N为场景总数; τsi、τsj为场景ωi和场景ωj下风电的功率值; πs、πs*、πi为场景ωs、ωs*、ωi发生的概率。
3 风光储参与市场交易的优化模型
3.1 基于风险中性的风光储独立参与市场优化模型
当三方独立参与市场时,风电、光伏和储能运营商追求各自利益最大化,储能运营商自愿决定是否与风电、光伏运营商进行购售电交易, 以补消风光功率预测不准确导致的正负差额电量,或者三者各自直接参与市场,这是三方优化决策问题。针对此问题建立数学优化模型。目标函数和约束条件具体如下。
3.1.1 目标函数
风电、光伏运营商均以自身净收益最大化为目标,售电收入包括市场售电收入、与储能交易收入; 成本包括正负偏差电量惩罚成本、运维成本、与储能交易成本。以风电目标函数为例,公式为
| $ \max \left(F_{\mathrm{w}}\right)=\pi_{\mathrm{w}}-C_{\mathrm{w}} $ | (3) |
| $ \left\{\begin{aligned} \pi_{\mathrm{W}}= & \sum\limits_{t=1}^{T} \lambda_{t}^{\mathrm{e}} P_{t}^{\mathrm{W}}+\sum\limits_{t=1}^{T} \lambda_{t}^{\mathrm{w}-\mathrm{es}} P_{t}^{\mathrm{w}-\mathrm{es}} \\ C_{\mathrm{W}}= & \sum\limits_{t=1}^{T}\left(\lambda_{t}^{\mathrm{up}} P_{t}^{\mathrm{w}, \text { up }}+\lambda_{t}^{\text {down }} P_{t}^{\mathrm{w}, \text { down }}\right)+ \\ & \sum\limits_{t=1}^{T} c_{\mathrm{om}}^{\mathrm{w}} P_{t}^{\mathrm{w}, \text { actual }}+\sum\limits_{t=1}^{T} \lambda_{t}^{\mathrm{es}-\mathrm{w}} P_{t}^{\mathrm{es}-\mathrm{w}} \end{aligned}\right. $ | (4) |
式中: FW、πW、CW——风电运营商的净收益、售电收入和成本;
T——总时段数;
λte、PtW——t时刻的市场出清价格和风电运营商申报的功率;
λtw-es、λtes-w——t时刻储能运营商向风电运营商购电和售电的价格;
Ptw-es、Ptes-w——t时刻储能运营商向风电运营商购电和售电的功率;
λtup、λtdown——t时刻风电运营商的单位正、负偏差惩罚价格;
Ptw, up、Ptw, down——t时刻风电运营商的正、负偏差功率;
comw——风电运营商的运维成本系数;
Ptw, actual——t时刻风电运营商的实际功率。
储能运营商以自身净收益最大化为目标,售电收入包括市场售电收入、与风光运营商交易收入; 成本包括运维成本、与风光运营商交易成本。因此,储能运营商参与市场的目标函数为
| $ \max \left(F_{\mathrm{ES}}\right)=\pi_{\mathrm{ES}}-C_{\mathrm{ES}} $ | (5) |
| $ \left\{\begin{array}{l} \pi_{\mathrm{ES}}=\sum\limits_{t=1}^{T} \lambda_{t}^{\mathrm{e}} P_{t}^{\mathrm{es}}+\sum\limits_{t=1}^{T} \lambda_{t}^{\mathrm{es}-\mathrm{w}} P_{t}^{\mathrm{es}-\mathrm{w}}+\sum\limits_{t=1}^{T} \lambda_{t}^{\mathrm{es}-\mathrm{p}} P_{t}^{\mathrm{es}-\mathrm{p}} \\ C_{\mathrm{ES}}=\sum\limits_{t=1}^{T} c_{\mathrm{om}}^{\mathrm{es}} P_{t}^{\mathrm{es}, \text { actual }}+\sum\limits_{t=1}^{T} \lambda_{t}^{\mathrm{w}-\mathrm{es}} P_{t}^{\mathrm{w}-\mathrm{es}}+\sum\limits_{t=1}^{T} \lambda_{t}^{\mathrm{p}-\mathrm{es}} P_{t}^{\mathrm{p}-\mathrm{es}} \end{array}\right. $ | (6) |
式中: FES、πES、CES——储能运营商的净收益、售电收入和成本;
Ptes、Ptes, actual——t时刻储能运营商申报的功率和实际功率;
λtes-p、λtp-es——t时刻储能运营商向光伏运营商售电和购电的价格;
Ptes-p、Ptp-es——t时刻储能运营商向光伏运营商售电和购电的功率;
comes——储能运营商的运维成本系数。
3.1.2 约束条件
约束条件包括风光运营商功率平衡约束和出力上下限约束,以及储能运营商的充放电功率约束和荷电状态约束。上述约束条件可表示为
| $ P_{t}^{\mathrm{w}, \text { actual }}-P_{t}^{\mathrm{w}}-P_{t}^{\mathrm{w}-\mathrm{es}}=P_{t}^{\mathrm{w}, \text { up }}-P_{t}^{\mathrm{w}, \text { down }} $ | (7) |
| $ P_{t}^{\mathrm{p}, \text { actual }}-P_{t}^{\mathrm{p}}-P_{t}^{\mathrm{p}-\mathrm{es}}=P_{t}^{\mathrm{p}, \text { up }}-P_{t}^{\mathrm{p}, \text { down }} $ | (8) |
| $ 0 \leqslant P_{t}^{\mathrm{w}} \leqslant P_{\mathrm{w}}^{\max } $ | (9) |
| $ 0 \leqslant P_{t}^{\mathrm{p}} \leqslant P_{\mathrm{p}}^{\max } $ | (10) |
| $ 0 \leqslant\left|P_{t}^{\mathrm{es}}\right| \leqslant P_{\mathrm{es}}^{\mathrm{c}, \max } $ | (11) |
| $ 0 \leqslant P_{t}^{\mathrm{es}} \leqslant P_{\mathrm{es}}^{\mathrm{d}, \max } $ | (12) |
| $ S_{\min } \leqslant S_{t} \leqslant S_{\max } $ | (13) |
| $ S_{t}^{0_+}=S_{t}^{0_-} $ | (14) |
式中: Ptp, actual——时刻光伏运营商的实际功率;
Ptp、Ptp-es——t时刻光伏运营商申报的功率和储能运营商向光伏运营商购电的功率;
Ptp, up、Ptp, down——t时刻光伏运营商的正、负偏差功率;
Pwmax、Ppmax——风电和光伏运营商的功率上限;
Pesc, max、Pesd, max——储能运营商最大充电功率和最大放电功率;
Smin、Smax——储能运营商最小荷电状态和最大荷电状态;
St、St0+、St0-——储能运营商在t时刻、t时刻前和t时刻后的荷电状态。
3.2 基于风险中性的风光储联合参与市场优化模型
3.2.1 目标函数
风光储运营商在联合模式下,以联合体总收益最大为目标,收入包括风光储在现货市场的交易收入、与储能运营商交易的收入; 成本包括风光运营商向储能运营商购电的成本、风光运营商的运维成本,以及正、负偏差电量惩罚成本。因此,风光储联合参与现货市场的目标函数为
| $ \max \left(F_{\mathrm{CO}}\right)=\pi_{\mathrm{CO}}-C_{\mathrm{CO}} $ | (15) |
| $ \pi_{\mathrm{CO}}=\pi_{\mathrm{CO}}^{\mathrm{m}}+\pi_{\mathrm{CO}}^{\mathrm{wp}-\mathrm{es}} $ | (16) |
| $ \pi_{\mathrm{CO}}^{\mathrm{m}}=\sum\limits_{t=1}^{T}\left[\lambda_{t}^{\mathrm{e}} \cdot\left(P_{t}^{\mathrm{w}}+P_{t}^{\mathrm{p}}+P_{t}^{\mathrm{es}}\right)\right] $ | (17) |
| $ \pi_{\mathrm{CO}}^{\mathrm{wp}-\mathrm{es}}=\sum\limits_{t=1}^{T}\left(\lambda_{t}^{\mathrm{wp}-\mathrm{es}} \cdot P_{t}^{\mathrm{wp}-\mathrm{es}}\right) $ | (18) |
| $ C_{\mathrm{CO}}=\sum\limits_{t=1}^{T} c_{\mathrm{om}}^{\mathrm{w}} P_{t}^{\mathrm{w}, \text { actual }}+\sum\limits_{t=1}^{T} c_{\mathrm{om}}^{\mathrm{p}} P_{t}^{\mathrm{p}, \text { actual }}+ \\ \quad \sum\limits_{t=1}^{T} c_{\mathrm{om}}^{\mathrm{es}} P_{t}^{\mathrm{es}, \text { actual }}+C_{\mathrm{CO}, \mathrm{C}}+C_{\mathrm{CO}}^{\mathrm{es}-\mathrm{wp}} $ | (19) |
| $ C_{\mathrm{CO}, \mathrm{C}}=\sum\limits_{t=1}^{T}\left(\lambda_{t}^{\mathrm{up}} P_{t}^{\mathrm{wp}, \text { up }}+\lambda_{t}^{\mathrm{down}} P_{t}^{\mathrm{wp}, \text { down }}\right) $ | (20) |
| $ C_{\mathrm{CO}}^{\mathrm{es}-\mathrm{wp}}=\sum\limits_{t=1}^{T}\left(\lambda_{t}^{\mathrm{es}-\mathrm{wp}} \cdot P_{t}^{\mathrm{es}-\mathrm{wp}}\right) $ | (21) |
式中: FCO、πCO、CCO——联合体的净收益、收入和成本;
πCOm、πCOwp-es——联合体在现货市场的收入、与储能运营商交易的收入;
λtwp-es、Ptwp-es——储能运营商向风光运营商购电的价格和功率;
comp——光伏运营商的运维成本系数;
CCO, C、CCOes-wp——联合体的偏差惩罚成本和风光运营商向储能运营商购电的成本;
Ptwp, up、Ptwp, down——t时刻风光运营商的正、负偏差功率;
λtes-wp、Ptes-wp——风光运营商向储能运营商购电的价格和功率。
3.2.2 约束条件
约束条件包括风光运营商功率平衡约束和出力上下限约束,以及储能运营商的充放电功率约束和荷电状态约束,公式与式(7)~式(14)相同。此外,还应满足三方合作参与市场的有效性约束,即合作参与约束和激励约束。也就是说,联合体参与市场的净总收益应大于三方独立参与市场净总收益之和。
联合体的净总收益满足
| $ F_{\mathrm{W}}+F_{\mathrm{P}}+F_{\mathrm{ES}}-F_{\mathrm{CO}} \leqslant 0 $ | (22) |
式中: FP——光伏运营商的净收益。
三方各自的净收益满足
| $ F_{\mathrm{W}}-F_{\mathrm{CO}, \mathrm{W}} \leqslant 0 $ | (23) |
| $ F_{\mathrm{P}}-F_{\mathrm{CO}, \mathrm{P}} \leqslant 0 $ | (24) |
| $ F_{\mathrm{ES}}-F_{\mathrm{CO}, \mathrm{ES}} \leqslant 0 $ | (25) |
式中: FCO, W、FCO, P、FCO, ES——联合模式下风、光、储运营商各自的净收益。
其中,风电净收益计算公式为
| $ \left\{\begin{array}{l} F_{\mathrm{CO}, \mathrm{W}}=\pi_{\mathrm{CO}, \mathrm{W}}-C_{\mathrm{CO}, \mathrm{W}} \\ \pi_{\mathrm{CO}, \mathrm{W}}=\pi_{\mathrm{CO}, \mathrm{W}}^{\mathrm{m}}+\pi_{\mathrm{CO}}^{\mathrm{w}-\mathrm{es}} \\ C_{\mathrm{CO}, \mathrm{W}}=\sum\limits_{t=1}^{T} c_{\mathrm{om}}^{\mathrm{w}} P_{\mathrm{co}, t}^{\mathrm{w}, \mathrm{actual}}+\sum\limits_{t=1}^{T}\left(\varphi \cdot C_{\mathrm{CO}, \mathrm{C}}^{t}\right) \\ \pi_{\mathrm{CO}, \mathrm{W}}^{\mathrm{m}}=\sum\limits_{t=1}^{T}\left(\lambda_{t}^{\mathrm{e}} \cdot P_{\mathrm{co}, t}^{\mathrm{w}}\right) \\ \pi_{\mathrm{CO}}^{\mathrm{w}-\mathrm{es}}=\sum\limits_{t=1}^{T}\left(\lambda_{t}^{\mathrm{w}-\mathrm{es}} \cdot \vartheta \cdot P_{\mathrm{co}, t}^{\mathrm{w}-\mathrm{es}}\right) \end{array}\right. $ | (26) |
式中: πCO, W、CCO, W——联合模式下风电运营商的收入和成本;
πCO, Wm、πCOw-es——联合模式下风电运营商在现货市场购买和销售剩余电力的成本和收入;
Pco, tw, actual——联合模式下t时刻风电运营商的实际功率;
φ——偏差成本的比例系数;
CCO, Ct——联合模式下风光运营商的偏差成本;
Pco, tw——联合模式下风电运营商申报的功率;
ϑ——风电运营商向储能运营商售电的比例系数;
Pco, tw-es——联合模式下风光运营商向储能运营商销售的剩余总电力。
光伏运营商的净收益计算模型与风电类似,文中不再赘述。
3.3 考虑条件风险价值的风光储联合参与市场交易优化模型
风光储联合参与市场,在决策中除了需考虑收益最大化外,还需综合考虑风光出力不确定性带来的风险。为此,本文采用CVaR法进行风险评估,建立考虑条件风险价值的风光储联合参与市场交易优化模型,规避均值-方差法无法区分正负偏差的缺陷,也可处理风险价值(Value at Risk, VaR)法无法评估尾部风险的问题。其中, 风光储联合体参与市场交易的CVaR表征在一定的置信水平和正常波动的市场下,决策者的决策组合所产生的预期损失超过VaR的条件均值[12]。具体计算公式如下
| $ G_{1-\beta}^{\mathrm{CVaR}}= E\left[f(x, y) \mid f(x, y) \leqslant G_{1-\beta}^{\mathrm{VaR}}\right]= \\ \quad\quad\quad\quad \frac{1}{\beta} \int_{-\infty}^{G_{1-\beta}^{\mathrm{CVaR}}} f(x, y) p(y) \mathrm{d} y $ | (27) |
| $ G_{1-\beta}^{\mathrm{VaR}}= \min [V \in R: P(y \leqslant V) \geqslant \beta] $ | (28) |
| $ E(f(x, y))=\sum\limits_{s=1}^{s} \rho_{s} f(x, y)_{s} $ | (29) |
式中: G1-βCVaR——风光运营商决策组合产生的预期损失超过VaR的条件均值;
β——风光运营商选取的置信水平;
E(f(x, y))——现货市场预期收益;
f(x, y)——风光收益函数集合;
x、y——决策变量和风光运营商决策过程中所面临的风险随机变量;
G1-βVaR——决策组合在将来的某一时间所面临的潜在最大损失值;
p(y)——风险随机变量的概率密度函数;
V——常数, 可取任意值;
R——实数集;
P(y)——风险随机变量的累计概率密度函数;
S、ρs——风光出力场景总数和场景s发生的概率;
f(x, y)s——场景s下的总收益。
为了便于CVaR的计算,引入松弛变量v, 并采用文献[13]提供的方法。具体计算公式如下
| $ F(y, v, \beta)=v+\frac{1}{\beta} \int_{y<v}(y-v) p(y) \mathrm{d} y $ | (30) |
式中: F(y, v, β)——引入松弛变量v后风光运营商决策组合产生的预期损失超过VaR的条件均值。
该函数相对于松弛变量v的最大值等于CVaR的值[14]。在参与市场时, 不同风光联合主体对待风险的厌恶程度不同, 因此引入CVaR理论描述该风险厌恶程度对收益的影响。其中:
| $ G_{1-\beta}^{\mathrm{CVaR}}=v+\frac{1}{\beta} \sum\limits_{s \in S} \rho_{s} \min \left(\pi_{\mathrm{co}}^{s}-C_{\mathrm{co}}^{s}-v, 0\right) $ | (31) |
式中: πcos、Ccos——场景s下联合模式的收入和成本。
式(31)为非线性函数,求解过程较为复杂,因此引入另一松弛变量zs将其线性化为
| $ \left\{\begin{array}{l} G_{1-\beta}^{\mathrm{CVaR}}=v+\frac{1}{\beta} \sum\limits_{s \in S} \rho_{s} z_{s} \\ z_{s} \leqslant \pi_{\mathrm{co}}^{s}-C_{\mathrm{co}}^{s}-v \\ z_{s} \leqslant 0 \end{array}\right. $ | (32) |
在风险评估的基础上,以预期收益最大为目标,以式(7)~式(14)为约束条件, 结合未考虑风险的情况, 建立考虑条件风险价值的风光储联合参与现货交易优化决策模式, 该目标函数表示为
| $ \max \left[\delta \sum\limits_{s=1}^{s} \rho_{s}\left(\pi_{\mathrm{co}}^{s}-C_{\mathrm{co}}^{s}\right)+(1-\delta)\left(v+\frac{1}{\beta} \sum\limits_{s \in S} \rho_{s} z_{s}\right)\right] $ | (33) |
式中: δ——风光主体在收益和风险之间的权衡系数,δ=1表示完全风险偏好,δ=0表示完全风险厌恶。
4 算例分析
4.1 算例描述
风光储参与市场模式、偏差惩罚价格、现货价格和可再生能源出力预测波动, 以及考虑条件风险价值下置信水平的设定是影响风光参与现货市场交易结果的因素。因此, 根据前文所建模型从以上4个角度设计算例, 计算风光储独立和联合参与市场的交易情况和收益情况, 进而分析风光储参与市场交易的最优策略。
风险中性情况下风光运营商功率、日前出清电价预测和风光出力典型场景参考文献[14]。考虑条件风险价值下, 风电出力不确定模型中的切入风速为3 m/s, 切出风速为26 m/s,额定风速为15 m/s; 光伏出力模型中的α和χ分别为0.4和8.5。储能运营商装机容量为10 MW/40 MWh,充放电效率分别为0.85和1, 年运维成本为10万元/MW; 偏差惩罚价格取为日前市场出清电价的1.2倍,弃电单位成本为600元/MWh。
4.2 风险中性情况下风光储交易结果分析
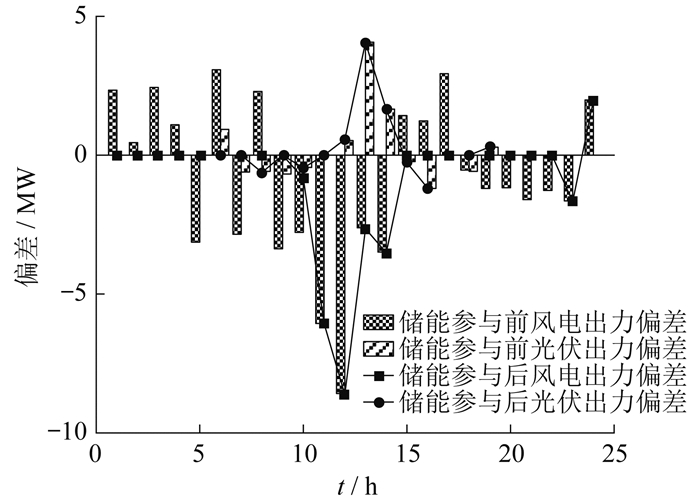
独立模式下,储能参与前后风电、光伏出力偏差如图 3所示。
由图 3可以看出,在独立模式下,风光运营商出力存在不确定性,风光参与市场交易时存在正负偏差; 储能机组在现货价格高的11:00—14:00时段独立参与市场,而在现货价格低的1:00—4:00时段购买风光进行充电。一方面平抑了风光出力偏差,另一方面也保证了储能运营商在现货价格高时有充足的电力来参与市场。
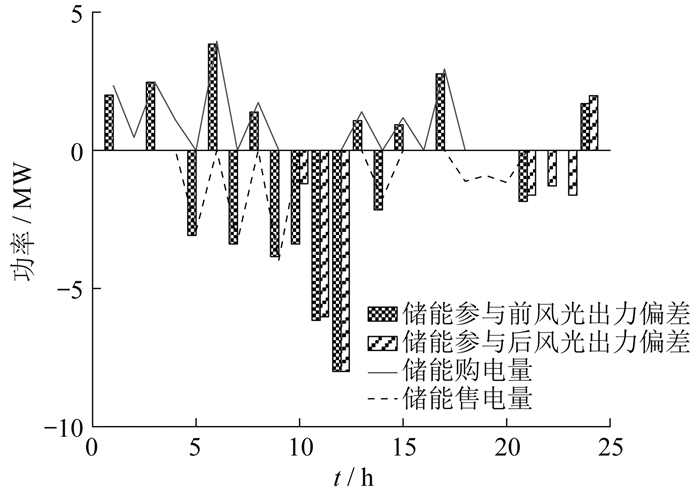
联合模式下,储能参与前后风电、光伏出力偏差,以及储能购售电量如图 4所示。
由图 4可以看出,在联合模式下,储能参与市场的方式为: 在1:00和3:00时刻, 风光存在正偏差, 储能机组充电; 在5:00、7:00和9:00时刻, 风光存在负偏差, 储能机组放电; 在16:00—19:00时段, 风光均无偏差,但此时为用电高峰期,储能机组需要放电来满足供需平衡。这一方式能够有效降低风光的出力偏差, 同时增加储能机组的收入和整个联合体的收益。
4.3 独立和联合参与市场收益情况分析
风光储独立参与市场时的收益情况如表 1所示。
表 1
风光储独立参与市场的收益情况
| 储能参与 | 风电 | 光伏 | 储能净收益 | |||
| 净收益 | 惩罚成本 | 净收益 | 惩罚成本 | |||
| 参与前 | 19 547.84 | 4 400.04 | 16 139.40 | 959.04 | ||
| 参与后 | 22 010.56 | 1 937.32 | 16 365.84 | 732.60 | 444.00 | |
风光储联合参与市场时的收益情况如表 2所示。
表 2
风光储联合参与市场收益情况
| 合作模式 | 风电和光伏 | 储能净收益 | |
| 净收益 | 惩罚成本 | ||
| 风光合作 | 36 322.16 | 4 521.40 | |
| 风光储合作 | 39 116.40 | 1 727.16 | 452.10 |
由表 1和表 2可以看出,在风光储独立参与市场模式下,风光运营商通过与储能运营商的交易能够降低因风光机组出力不确定性产生的惩罚成本,如风电运营商的惩罚成本在储能参与后降低了14.7%,光伏运营商的惩罚成本在储能参与后降低了24.0%。风光储独立和联合模式下收益有所差别的原因是, 储能运营商参与市场的方式不同。在独立模式下, 储能独自参与市场,而在联合模式下,储能用于平抑风光偏差。风光在独立模式下总的偏差惩罚费用比联合模式下高62.0%。由此说明, 联合模式下储能对于风光波动性和不确定性的平抑具有更好的效果,从而给联合体带来更大的收益。
4.4 不同偏差惩罚价格下独立和联合模式的交易结果分析
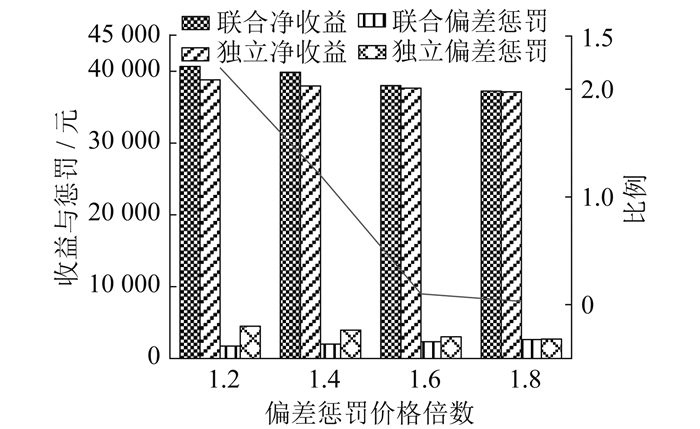
不同偏差惩罚价格下独立和联合模式的交易结果如图 5所示。其中, 折线表示独立模式下储能直接参与市场的部分与储能参与调节风光偏差的部分的比例。
由图 5可以看出,在独立模式下,当偏差惩罚价格为现货价格的1.2倍时,风光偏差产生的惩罚较低,储能以独立参与市场的方式来获得最大收益,因此风光偏差无法避免;随着偏差惩罚价格的升高,风光运营商选择向储能支付更高的费用来避免偏差惩罚,储能基于最大收益的目标选择与风光运营商进行交易,因此对风光偏差的平抑效果越来越好。当偏差惩罚价格增高到1.6倍时,风光储独立和联合参与市场的收益趋于一致,这是由于在高偏差惩罚价格下,储能在两种模式下都会积极参与风光的平抑,导致风光的偏差惩罚在两种模式下均有所降低,因此收益逐渐趋于一致。
4.5 现货价格和风光出力预测偏差对联合模式的收益影响分析
为了进一步研究现货价格和风光出力预测偏差水平对联合模式下市场交易收益的影响,本文设置了6种场景,并进行仿真分析。6种场景设置如表 3所示。
表 3
6种现货价格和风光出力预测偏差场景设置
| 场景 | 现货价格倍数 | 风光出力预测偏差水平/% |
| 1 | 0.8 | 0 |
| 2 | 1.0 | 0 |
| 3 | 1.2 | 0 |
| 4 | 1.0 | 5 |
| 5 | 1.0 | 15 |
| 6 | 1.0 | 30 |
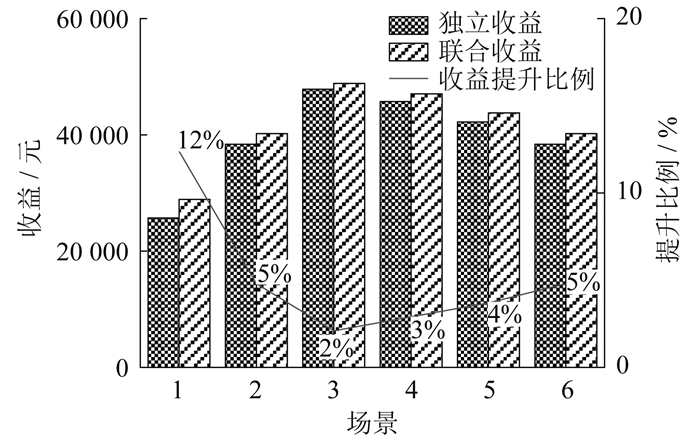
6种场景下风光储独立和联合参与市场的收益情况如图 6所示。
分析图 6数据可得出以下结论。
(1) 在现货价格不同和风光出力预测存在偏差的各个场景下,联合模式下的收益均高于独立模式。这表明储能和风光存在一定的互补特性,通过联合的方式可以提高收益。
(2) 对比场景1、2、3下的收益可知,联合和独立模式下的收益均与现货价格成正相关,但收益提升比例会随着现货价格的增高而越来越低,如在场景1和场景3下,收益提升比例由12%降到2%。其原因是风光运营商的功率受到风速和光照的影响,且存在装机容量的限制,即使在高现货价格下,风光运营商无风光资源或容量可用,收益提升比例达到瓶颈。
(3) 由场景4、5、6结果可知,随着风光预测偏差的减小,独立和联合模式的总收益均会提高,但储能运营商对于联合模式下的收益提升效果越来越差。其原因是当风光预测偏差较小时,联合模式下储能运营商受到联合体的限制,削弱了独立参与市场的能力,同时储能机组灵活的充放电特性也得不到充分利用,从而使得联合模式下的收益提升比例越来越低。
4.6 风险非中性情况下的风光储交易结果及收益分析
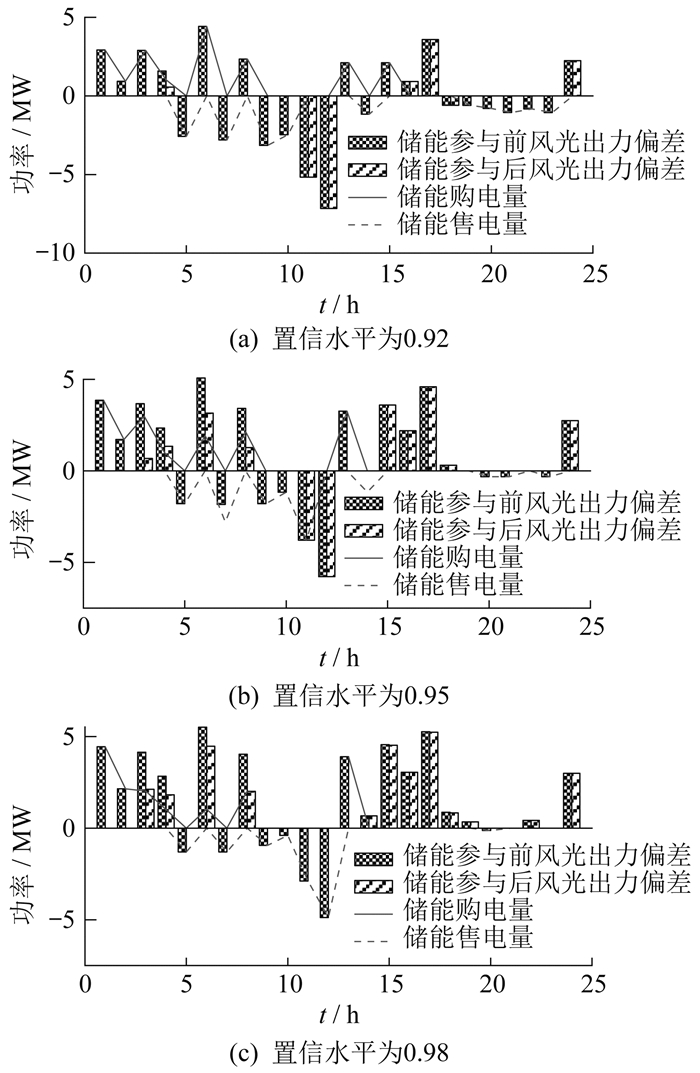
不同置信水平下风光储的交易结果如图 7所示。
由图 7可以看出,当置信水平为0.92时,为了降低风光出力不确定带来的风险,与风险中性的情况相比,风光出力偏差有所降低,其正负偏差仍由储能运营商通过购售电来平抑;随着置信水平进一步提高,对应风光较低的风险水平,风光出力偏差进一步降低。
不同置信水平下风光储运营商的收益情况如图 8所示。
由图 8可以看出, 置信水平为0.95时, 风光出力偏差的降低导致了惩罚成本的降低,净收益较0.92的置信水平提升了978.28元。当置信水平为0.98时,由于风光运营商参与市场交易的策略更为保守,其在市场交易的电量相较于置信水平为0.95时进一步降低,导致风光出现更多的偏差电量,但储能运营商容量有限,对风光偏差电量的调节能力不足,其偏差成本相较于置信水平为0.95时反而有所提高,同时风光总收益也明显下降。因此,为了保证风光储运营商的收益,要适当设置置信水平来计量风险。
5 结语
本文构造了风光储独立和联合参与市场的交易策略框架,以预期收益最大为目标建立了风光储独立、联合和考虑条件风险价值联合模式下参与市场交易的数学模型,对比分析了参与市场方式、现货价格、偏差惩罚价格、风光出力预测偏差水平、置信水平对运营商收益情况的影响。储能机组利用其充放电特性来平抑风光的出力正负偏差, 从而提升市场主体收益;偏差惩罚价格或单位弃电损失的大小是影响储能平抑风光效果的重要因素,高偏差惩罚价格或弃电损失下,平抑效果更好,反之更差;置信水平与收益并不是绝对的正相关,当置信水平更高时,风光运营商参与市场的交易态度就会更加保守,反而不利于其消纳, 造成更大的损失。
参考文献
-
[1]康重庆, 姚良忠. 高比例可再生能源电力系统的关键科学问题与理论研究框架[J]. 电力系统自动化, 2017, 41(9): 2-11.
-
[2]ZHANG N, HU Z G, HAN X, et al. A fuzzy chance-constrained program for unit commitment problem considering demand response, electric vehicle and wind power[J]. International Journal of Electrical Power & Energy Systems, 2015, 65(2): 201-209.
-
[3]TAN Z F, YANG S B, LIN H Y, et al. Multi-scenario operation optimization model for park integrated energy system based on multi-energy demand response[J]. Sustainable Cities and Society, 2020, 53: 101973. DOI:10.1016/j.scs.2019.101973
-
[4]德格吉日夫, 谭忠富, 李梦露, 等. 考虑不确定性的风储电站参与电力现货市场竞价策略[J]. 电网技术, 2019, 43(8): 2799-2807.
-
[5]王振浩, 马爽, 李国庆, 等. 考虑复合储能电站接入的电网日前-日内两阶段滚动优化调度[J]. 太阳能学报, 2022, 43(10): 400-408.
-
[6]徐立新, 沈志钧, 刘明波, 等. 考虑配电网安全校核的分布式能源聚合商参与市场竞标的双层混合整数优化模型[J]. 电网技术, 2021, 45(11): 4395-4406.
-
[7]刘佳楠, 熊宁, 朱文广, 等. 电力市场环境下风光储联合运行优化策略[J]. 电力科学与技术学报, 2017, 32(1): 11-15.
-
[8]孙波, 樊亚南, 李志恒, 等. 偏差电量考核下风光储混合发电商的市场均衡博弈研究[J]. 水电能源科学, 2020, 38(2): 202-205.
-
[9]王凯, 延肖何, 蒋凯, 等. 考虑碳交易的风光储场站参与电力现货市场报价策略与调控方法[J]. 中国电机工程学报, 2023, 43(18): 7091-7103.
-
[10]王洪亮, 孙伟卿, 桑丙玉. 考虑条件风险价值的"新能源+储能"电站现货市场投标策略[J]. 电网技术, 2023, 47(9): 3620-3631.
-
[11]邢通. 大规模风电参与电力市场交易机制及优化模型研究[D]. 北京: 华北电力大学, 2020.
-
[12]杨波, 汤文成, 吴福保, 等. 考虑CVaR的"新能源+储能"电厂日前市场投标策略[J]. 电力系统保护与控制, 2022, 50(9): 93-100.
-
[13]ROCKAFELLAR R T, URYASEV S. Optimization of conditional value-at-risk[J]. Journal of Risk, 2000, 2(3): 21-41.
-
[14]KROKHMAL P, PALMQUIST J, URYASEV S. Portfolio optimization with conditional risk objectives and constraints[J]. Journal of Risk, 2002, 4(3): 43-68.