|
|
|
发布时间: 2024-04-28 |
特约专栏:新型源荷与配电网互动技术 |
|
|
|
收稿日期: 2024-03-24
中图法分类号: TM73
文献标识码: A
文章编号: 2096-8299(2024)02-0102-07
|
摘要
OP互联是指供电企业内部对电力调度系统(OMS)及设备(资产)运维精益管理系统(PMS)中维护的台账数据进行有效关联。针对中压配电网10 kV馈线OP互联流程复杂、效率低下,且缺乏有效校验机制等问题,提出了一种基于配电网多源量测数据与系统台账信息的馈线OP数据校核与匹配方法。首先,从OMS和PMS中提取功率、设备参数等信息,并对台账及功率进行预处理,形成功率时间序列矩阵;然后,基于α-DDTW距离评估两侧馈线功率波形近似度,实现馈线OP数据的校核与关联匹配;最后,对华东某市电力公司的系统数据进行算例分析,验证了所提方法的有效性与实际工程应用价值。
关键词
OP数据互联; α-DDTW算法; 波形相似度; 配电网
Abstract
OP interconnection refers to the effective correlation of ledger data maintained in the Operation Management System(OMS)and the Power Production Management System(PMS) within the power supply enterprise. It serves as the foundation for enhancing the level of grid management and production efficiency. Addressing the complexities and inefficiencies in the OP interconnection process for 10 kV feeder lines in the medium-voltage distribution network, as well as the lack of effective verification mechanisms, a method for verifying and matching OP data for feeder lines based on multi-source measurement data and system ledger information of the distribution network is proposed. Firstly, power information and equipment parameters are extracted from the OMS and PMS systems, and ledger and power are preprocessed to form a successful time-series matrix. Then, based on α-DDTW distance, the similarity of power waveforms on both sides of the feeder line is evaluated, automatically achieving verification and correlation matching of feeder line OP data. Finally, through case analysis using actual system data from a power company in East China, the effectiveness and practical engineering application value of the proposed method are validated.
Key words
OP data interconnection; α-DDTW algorithm; waveform similarity; distribution network
OP互联是指将调度管理系统(Operation Management System,OMS)与设备(资产)运维精益管理系统(Power Production Management System,PMS)中同一设备的异构数据进行关联与融合的数据贯通过程。该过程覆盖输配电全域资源信息。其中,中压配电网10 kV大馈线(以下简称馈线)处于地市调度与运检部门管辖范围的交界点,是将35 kV及以上电压等级变电站电能分配至末端380 V低压用户的主纽带,其OP台账参数贯通程度和精益化管理水平直接影响到线路故障定位、月度停电检修计划、线路投运与变更等配调协同业务工作的正常开展,对支撑业数融合与推进泛在电力物联网建设具有重要意义[1]。
在实际电网运营中往往存在如下问题:首先,电网调度与设备管理分属两个部门,业务相对独立,因采用了不同的标准和格式定义方式,导致存量台账数据难以无缝衔接;其次,电力网络安全分区使得核心业务系统对外保持物理隔离,客观上阻碍了数据的共享;最后,因人为疏漏导致信息在录入过程中出现错位和失真的情况也难以避免。
OP互联在业务上属于营配调贯通工作的一环,本质上是对系统中多源异构数据建立正确的映射关系。目前,数据贯通工作主要分为人工匹配、优化业务流程、重构数据模型、针对性设计关联算法等4个方面。因数据贯通工作主要依赖于人工现场普查、梳理设备档案信息的手动匹配方式[2],在任务繁重的情况下会降低专职人员工作效率,难以保障匹配结果的完整性和准确性。文献[3]在数据治理工作中添加了考核与竞赛机制,既增加了人力成本投入,又难以应对新型电力系统下爆发式增长的海量数据。文献[4]针对异常数据溯源与数据交互困难,设计了一套营配调数据互通体系,但此业务流程架构繁杂,跨部门间的高频协作易发生责任推卸、办公效率降低等问题,且需要较长时间验证其成效,难以实现自动化及大范围推广。文献[5]针对源端系统数据模型的局限性,采用IEC 61850标准对变电站与调度中心远程通信模型进行了可行性分析,但该方法对数据传输格式要求严格,难以泛化至其他系统。文献[6]针对营配网末端设备建模不统一的问题,设计了末端设备公共信息模型。文献[7]基于文本一致性算法,根据设备名称、电压等级等信息,对营销系统与PMS进行了贯通质量核查。文献[8]通过业务系统台账名称匹配情况,实现了数据一致性校核。文献[9]基于知识图谱技术对营配系统中的拓扑数据进行了校验。这些方法主要倾向于挖掘台账文本信息,对于映射结果准确性均缺乏基于电气机理的校验机制。
本文提出了基于α衍生动态时间规整(α-Derivative Dynamic Time Warping,α-DDTW)算法与波形相似度的馈线OP数据校核匹配方法。该方法充分利用功率量测数据和系统台账信息,通过计算调度侧馈线负荷与设备侧同一馈线下配电变压器(以下简称“配变”)总功率的一致性,进行校核与精准关联匹配。通过在华东某市电力公司实际数据治理工作中加以运用,证明该方法解决了调控云与电网资源业务中台馈线信息关联异常问题,支撑了电网一张图数据流实质贯通。
1 馈线OP互联概述
1.1 传统馈线OP互联方法
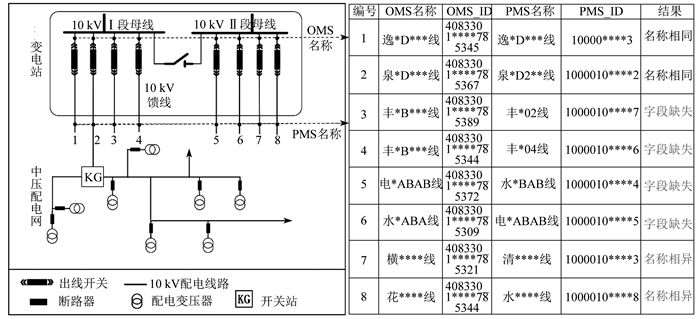
目前,馈线台账参数的OP互联主要基于文本模糊匹配,即关联流程中OMS将封装有设备档案信息的电系铭牌CIM/E文件发送至PMS,通过计算两侧名称字符串相似度建立映射关系。该方法仅对两侧系统命名规范且相同的线路有效,对因历史遗留问题而导致的语义异构和同源异名现象,则需要依赖人工对档案溯源并加以判断。根据GB/T 33601—2017《电网设备通用模型数据命名规范》[10]中的相关规定,中压配电馈线多以其供电覆盖区域地名简称进行自然命名,地理位置接近的不同馈线命名具有极高同质性,如“**B*02线”“**B*04线“,若某馈线在一侧系统维护值存在字段缺失,则匹配异常的风险将大幅增加。因此,仅依靠单一的文本相似性匹配具有局限性,关联准确率较低。
基于文本相似性的10 kV馈线OP互联如图 1所示。
1.2 数据基础
随着配电网量测设备部署的不断完善与信息通信水平的不断提高[11],各类智能量测、通信设备通过接入电力系统,使得电网公司可以获取馈线及配变的大量实时或历史量测数据[12]。这些数据为馈线OP互联提供了数据基础。在实际运行中,两个部门对于馈线运行数据有不同的采集倾向,调度部门采集的数据主要来源于各条馈线的负荷,设备部门则是对馈线末端的配变进行数据采集。从OMS与PMS获得的相关量测及设备数据如下。
(1)设备台账信息。从PMS系统获取馈线名称、馈线PMS_ID、配变名称、配变PMS_ID、配变地址、配变与馈线从属关系信息等。从调控云系统获取调度名称馈线名称、馈线OMS_ID及其量测点ID。
(2)馈线历史量测数据。基于数据库主键关联原则,组合拼接PMS与营销系统各数据表后,得到设备侧每条馈线下挂接的各台配变的电压、有功功率、无功功率数据,形成配变有功矩阵 Ppbe= [Ppb,t,ne]T×N(t=1,2,3,…,T,T为总计量的时间断面数;n=1,2,3,…N,N为变压器数量)。配变无功矩阵 Qpbe=[Qpb,t,ne]T×N。从调度云系统导出馈线负荷数据,生成馈线调度侧有功矩阵 Pkxo=[Pkx,t,mo]T×M(m=1,2,3,…M,M为馈线数量),馈线调度侧无功矩阵Qkxo =[Qkx,t,mo]T×M,最终生成功率时间序列。采集数据生成功率时间序列流程如图 2所示。
2 基于α-DDTW算法的功率相关性计算
2.1 功率相关性判别技术
在配电网实际运行中,不同馈线间的功率波形存在较为明显的差异,而对于同一条馈线,其传输电能应与所属配变消耗的总电能遵循能量守恒定律,在时间尺度上表现出功率波形的高度一致性。因此,可利用功率波形相似度对两个系统中已匹配的馈线信息进行校验,同时,对未能成功匹配的馈线进行再次匹配。
2.2 基于α-DDTW算法的功率匹配技术
在实际工程中,由于配电网量测设备繁多、设备差异较大、信息传输设备故障等原因,会导致时钟采样不同步,进而出现时钟偏移、数据损坏,以及采集到的功率时间序列数据缺失等问题[13],因而使用传统基于欧氏距离对采集到的功率波形进行相关性计算已不再适用。
动态时间规整(Dynamic Time Warping,DTW)算法是语音识别领域的常用算法[14],主要应用于孤立词语音识别,是衡量两条长度不等曲线相似度的常用方法[15]。本文所使用的α-DDTW算法是在传统DTW算法基础上对采集数据进行预处理,以减少因功率数据缺失、波形时钟偏移而造成的影响。首先,利用斜率和标准化思想提取功率波形特征和变化趋势;然后,利用动态正则化思想调整两个电压序列不同时间点元素之间的对应关系,找出两个时间序列对应元素之间的相似点,并对这些点的距离求和,求出规整路径;最后,通过比较找到最优的规整路径,以此衡量两个时间序列之间的相似性[16]。
在馈线OP互联中,使用α-DDTW算法进行规整路径计算。首先,在OMS中,获取馈线侧历史功率量测数据,并根据时间形成馈线侧功率时间序列So;然后,对于PMS中获取的数据,先根据配变量测数据及相关参数计算高压侧功率;最后,根据一条馈线下对应的所有配变高压侧功率总和,求取该馈线的设备侧功率。具体计算公式为
| $ \begin{gathered} S_{{\mathrm{pbh}}, n}=S_{{\mathrm{pbl}}, n}+\Delta S_0+\Delta S_{{\mathrm{T}}} \\ \end{gathered} $ | (1) |
| $ S_{{\mathrm{p}}}=\sum\limits_{i=1}^a S_{{\mathrm{pbh}}, n} $ | (2) |
式中:Spbh,n——第n台配变的高压侧功率;
Spbl,n——第n台配变的低压侧功率;
∆S0——配变励磁损耗;
∆ST——配变绕组损耗;
Sp——馈线对应的设备侧功率时间序列;
a——该条馈线下挂接的配变数量。
配电网正常运行情况下,馈线首端到配变低压侧的功率损耗主要由配变自身损耗引起,包含励磁损耗与绕组损耗。将低压侧功率折合至高压侧后再进行累加,可以更准确表征馈线的实际功率。
对So和Sp进行预处理,得到馈线侧和设备侧预处理功率时间序列Sop和Spp,为
| $ \begin{aligned} & S_{{\mathrm{o}}=}^{{\mathrm{p}}}= \\ & \left\{\begin{array}{lc} S_{{\mathrm{o}} i}^{{\mathrm{p}}}=\frac{\left(S_{{\mathrm{o}} i}-S_{{\mathrm{o}}(i-1)}\right)+\left(S_{{\mathrm{o}}(i+1)}-S_{{\mathrm{o}}(i-1)}\right) / 2}{2}, & i=2,3,4, \cdots L_1-1 \\ S_{{\mathrm{o}} i}^{{\mathrm{p}}}=S_{{\mathrm{o}} 2}-S_{{\mathrm{o}} 1}, & i=1 \\ S_{{\mathrm{o}} i}^{{\mathrm{p}}}=S_{{\mathrm{o}} L_1}-S_{{\mathrm{o}}\left(L_1-1\right)}, & i=L_1 \end{array}\right. \end{aligned} $ | (3) |
| $ \begin{aligned} & S_{{\mathrm{p}}}^{{\mathrm{p}}} =\\ & \left\{\begin{array}{lc} S_{{\mathrm{p}} j}^{{\mathrm{p}}}=\frac{\left(S_{{\mathrm{p}} j}-S_{{\mathrm{p}}(j-1)}\right)+\left(S_{{\mathrm{p}}(j+1)}-S_{{\mathrm{p}}(j-1)}\right) / 2}{2}, & j=2,3,4, \cdots L_2-1 \\ S_{{\mathrm{p}} j}^{{\mathrm{p}}}=S_{{\mathrm{p}} 2}-S_{{\mathrm{p}} 1}, & j=1 \\ S_{{\mathrm{p}} j}^{{\mathrm{p}}}=S_{{\mathrm{p}} L_2}-S_{{\mathrm{p}}\left(L_2-1\right)}, & j=L_2 \end{array}\right. \end{aligned} $ | (4) |
式中:soip——Sop中第i个元素的值,i=1,2,3,…,L1;
soi——So中第i个元素的值;
L1,L2——So和Sp中元素个数;
spjp——Spp中第j个元素的值,j=1,2,3,…,L2;
spj——Sp中第j个元素的值。
进一步对其进行标准化处理,其公式为
| $ \begin{aligned} s_{{\mathrm{o}} i}^{{\mathrm{s}}}=\frac{s_{{\mathrm{o}} i}^{{\mathrm{p}}}-\mu_{{\mathrm{o}}}}{\sigma_{{\mathrm{o}}}} \\ \end{aligned} $ | (5) |
| $ s_{{\mathrm{p}} j}^{{\mathrm{s}}}=\frac{s_{{\mathrm{p}} j}^{{\mathrm{p}}}-\mu_{{\mathrm{p}}}}{\sigma_{{\mathrm{p}}}} $ | (6) |
式中:sois——新的功率时间序列Sos中第i个元素的值;
μo,μp——Sop和Spp均值;
σo,σp——Sop和Spp方差;
spjs——新的功率时间序列Sps中第j个元素的值。
对Sos和Sps进行标准化处理,建立α-DDTW距离矩阵,从而找到最优规整路径,计算公式为
| $ {\boldsymbol{d}}\left(S_{{\mathrm{o}}}^{{\mathrm{s}}}, S_{{\mathrm{p}}}^{{\mathrm{s}}}\right)=\left\{\begin{array}{l} \left(s_{{\mathrm{o}} 1}^{{\mathrm{s}}}-s_{{\mathrm{p}} 1}^{{\mathrm{s}}}\right)^2, \quad L_1=1, L_2=1 \\ \left(s_{{\mathrm{o}} 1}^{{\mathrm{s}}}-s_{{\mathrm{p}} L_2}^{{\mathrm{s}}}\right)^2+d\left(1, L_2-1\right), L_1=1, L_2>1 \\ \left(s_{{\mathrm{o}} L_1}^{{\mathrm{s}}}-s_{{\mathrm{p}} 1}^{{\mathrm{s}}}\right)^2+d\left(L_1-1,1\right), L_2=1, L_1>1 \\ \left(s_{{\mathrm{o}} L_1}^{{\mathrm{s}}}-s_{{\mathrm{p}} L_2}^{{\mathrm{s}}}\right)^2+\min \left\{d\left(L_1-1, L_2\right),\right. \\ \left.d\left(L_1, L_2-1\right), d\left(L_1-1, L_2-1\right)\right\}, \quad L_1 、L_2>1 \end{array}\right. $ | (7) |
式中:d(·)——两个功率时间序列之间的α-DDTW距离。
计算衰减系数r为
| $ r=1-\frac{l \times l}{L_1 L_2} $ | (8) |
式中:l——功率时间序列So和Sp最长公共子串。
获取So和Sp的α-DDTW距离为
| $ d\left(S_{{\mathrm{o}}}, S_{{\mathrm{p}}}\right)=r \times \sqrt{d\left(S_{{\mathrm{o}}}^{{\mathrm{s}}}, S_{{\mathrm{p}}}^{{\mathrm{s}}}\right)} $ | (9) |
形成两侧α-DDTW距离矩阵为
| $ {\boldsymbol{D}}_{{\mathrm{o}}-{\mathrm{p}}}=\left[\begin{array}{cccc} d_{1,1} & d_{1,2} & \cdots & d_{1, v} \\ d_{2,1} & d_{2,2} & \cdots & d_{2, v} \\ \vdots & \vdots & & \vdots \\ d_{c, 1} & d_{c, 2} & \cdots & d_{c, v} \end{array}\right] $ | (10) |
式中:v——设备侧馈线数量;
c——调度侧馈线数量;
dc,v——馈线侧和设备侧功率时间序列曲线间的α-DDTW距离。
将上述α-DDTW距离矩阵按行进行分块为
| $ \begin{gathered} \boldsymbol{D}_{{\mathrm{o}}-{\mathrm{p}}}=\left[\begin{array}{lllll} \boldsymbol{D}_1 & \boldsymbol{D}_2 & \boldsymbol{D}_3 & \cdots & \boldsymbol{D}_c \end{array}\right]^{{\mathrm{T}}} \\ \end{gathered} $ | (11) |
| $ \boldsymbol{D}_k=\left[\begin{array}{lllll} d_{k, 1} & d_{k, 2} & d_{k, 3} & \cdots & d_{k, v} \end{array}\right], k=1,2,3, \cdots c $ | (12) |
每个分块矩阵代表调度侧某馈线与设备侧所有馈线之间的α-DDTW距离。通过比较分块矩阵中元素值的大小,即可判断两侧功率时间序列曲线的相似性。元素值越小,则两侧对应馈线信息匹配度越高。
2.3 功率波形相似度匹配评价指标
本文研究的馈线OP互联匹配是基于实际测量的功率波形,依据波形之间的相似性对两侧系统间馈线名称进行匹配。为量化波形之间的相似性指标,可以根据α-DDTW距离,计算匹配馈线两侧功率时间序列曲线间的相关性。相关性系数p的计算公式为
| $ p=\frac{1}{1+d_{c v}} $ | (13) |
式中:dcv——两侧已匹配馈线α-DDTW距离。
p值位于[0, 1]之间,指标越大,则功率相关性越高,功率波形相似性越高,匹配效果越好。
对于传统文本匹配算法的功率相关性计算亦可遵循上述计算方法。首先,根据文本匹配结果,取对应两侧馈线的功率数据作为功率时间序列So和Sp;然后,应用前文提出的基于α-DDTW算法的功率匹配技术,计算传统文本匹配算法匹配的馈线α-DDTW距离,从而得出两侧已匹配馈线的功率相关性。
以相关性系数p > 0.85为判断标准,对匹配信息正确性进行验证。若p大于0.85,则认为匹配结果正确;若p小于0.85,则认为匹配结果错误。匹配结果的准确性δ表示为
| $ \delta=\frac{n_{{\mathrm{TR}}}}{n_{{\mathrm{TR}}}+n_{{\mathrm{FL}}}} \times 100 \% $ | (14) |
式中:nTR——正确识别的信息数量;
nFL——错误识别的信息数量。
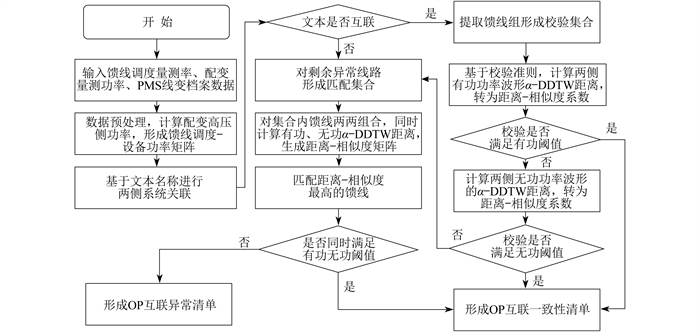
2.4 功率相关性OP互联流程
首先,输入馈线调度量测功率、配变量测功率以及PMS线变档案数据,对数据进行预处理,得出配变高压侧功率,形成馈线调度-设备功率矩阵。其次,依据传统文本匹配算法进行两侧系统馈线名称文本互联;对于不可互联匹配的馈\线,加入剩余异常线路的匹配集合;对于可互联匹配的馈线,提取馈线组形成校验集合。然后,分别计算两侧有功功率波形α-DDTW距离和无功功率波形α-DDTW距离,继而进行距离-相似度系数计算,若有任一相似度系数满足校验条件,则输出形成OP互联一致性清单;对于二者均不满足的馈线组,并入剩余异常线路匹配集合。最后,对集合内馈线两两组合,计算有功无功α-DDTW距离,生成距离-相似度矩阵,并匹配距离-相似度最高的馈线,判断其有功、无功相似度系数是否同时满足校验条件。若不满足校验条件,则输出形成OP互联异常清单;若满足校验条件,则输出形成OP互联一致性清单。功率相关性OP互联流程如图 3所示。
3 算例分析
3.1 算例数据获取
3.2 功率波形相似度匹配效果分析
基于α-DDTW算法计算功率曲线相似度,可对两侧馈线进行匹配。匹配结果如表 2所示。
表 2
基于功率波形相似度匹配结果
| 设备侧名称 | 调度侧名称 | 相关性/% | 有功偏差/% |
| 银*****线 | 爱*****线 | 99.98 | 0.43 |
| 丹*****线 | 剧*****线 | 99.92 | 0.27 |
| 苗*****线 | 苗*****线 | 99.95 | 0.35 |
| 杭****线 | 杭*****线 | 99.91 | 0.97 |
| *水****线 | *水****线 | 99.36 | 4.14 |
| 行****线 | 行*****线 | 99.92 | 1.34 |
| 和*****线 | 华*****线 | 99.69 | 1.22 |
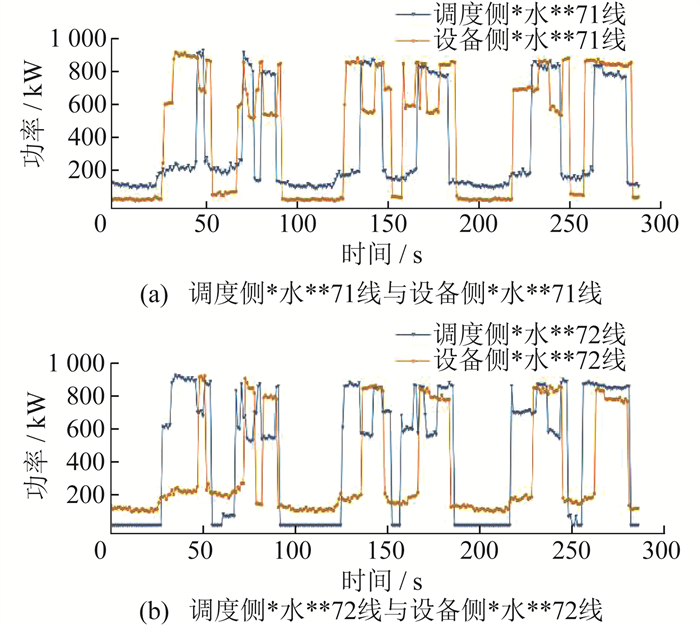
其中,以设备侧“*水**71线”和调度侧“*水**72线”为例,基于传统文本匹配算法匹配出馈线。基于文本匹配结果的两侧功率波形对比如 图 4所示。
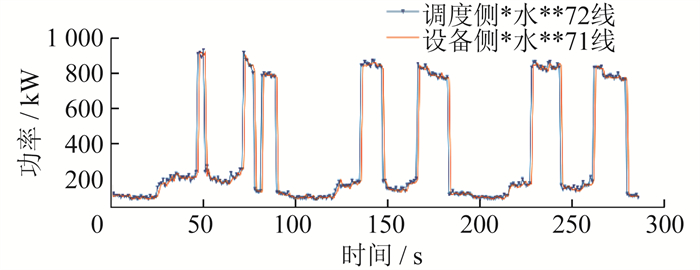
基于功率波形相似度匹配结果的波形对比如 图 5所示。
由图 4、图 5可以看出,基于传统文本匹配算法匹配的两侧馈线,其功率波形存在明显差异,出现了匹配错误。
本文所提方法与其他方法的匹配结果准确率对比如表 3所示。
表 3
不同识别方法匹配结果准确率对比
| 方法 | 准确率/% |
| 传统文本匹配算法 | 66.8 |
| 传统DTW算法 | 93.2 |
| α-DDTW算法 | 97.8 |
由表 3可以看出,无论是传统DTW算法还是改进后的α-DDTW算法,其识别结果准确率均明显优于传统文本匹配算法。
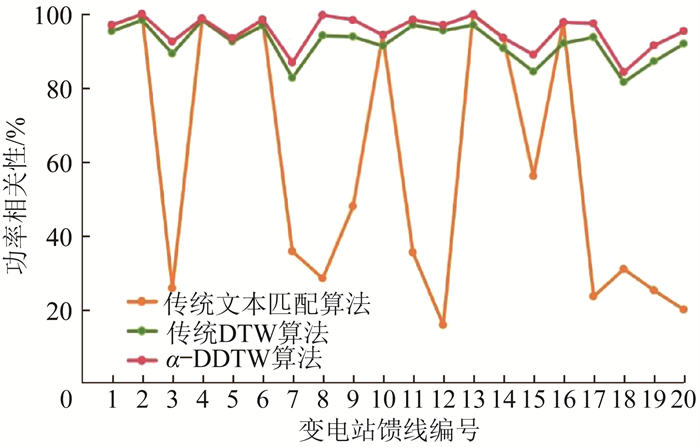
为进一步验证所提方法的有效性,对华东某市某变电站内已有的20条馈线与算法匹配结果之间的功率相关性进行对比,具体如图 6所示。
从图 6可以看出,α-DDTW算法计算得出的功率相关性略优于传统DTW算法。总之,基于α-DDTW算法对功率曲线相似度进行OP互联不仅准确率更高,而且具有更高鲁棒性,易于推广。
4 结论
针对实际工程中因OMS与PMS信息不互通导致两侧同一馈线信息不匹配的问题,本文提出了一种基于配电网多源量测数据与系统台账信息的馈线OP数据校核与匹配方法。首先,对设备侧的配变低压侧数据进行处理,得到设备侧馈线数据;然后,使用α-DDTW算法找出与调度侧相匹配的设备侧馈线;最后,运用华东某市电力公司的数据进行方法有效性验证,得到如下结论。
(1)本文所提方法能够通过分析功率波形相似度将OMS和PMS中同一馈线进行匹配。
(2)与传统文本匹配算法相比,本文所提方法摆脱了对馈线名称的文本依赖,对台账信息中馈线名称完全不一致的馈线也能进行匹配,具有较高的适应性。
(3)与传统DTW算法相比,本文所提方法降低了数据缺失、时钟偏移等问题对数据的预处理的影响,具有较高的匹配准确性和鲁棒性。
参考文献
-
[1]周峰, 周晖, 刁赢龙. 泛在电力物联网智能感知关键技术发展思路[J]. 中国电机工程学报, 2020, 40(1): 70-82.
-
[2]董寒宇, 朱晓黎, 相倩芸. 浅谈湖州公司营配贯通基础数据的维护[J]. 湖州师范学院学报, 2015, 37(2): 55-58.
-
[3]李君秋, 朱岩, 阴晓光. 以提质增效为目标的电网关键业务贯通与优化管理[J]. 企业管理, 2019(增刊1): 110-111.
-
[4]郑中胜, 王海伟, 石卓. 营配调源业务系统数据质量管理[J]. 电工技术, 2018(12): 33-34.
-
[5]王文龙. IEC 61850标准作为变电站出站远动协议的可行性分析[J]. 电力系统自动化, 2012, 36(17): 109-112.
-
[6]刘玉玺, 欧阳红, 李刚, 等. 基于IEC-CIM的营配网末端设备公共信息模型设计[J]. 智慧电力, 2019, 47(2): 75-81.
-
[7]邱林, 李爱民, 杨李达. 营配调贯通数据质量分析方法及自动化实现的研究和应用[J]. 电子技术与软件工程, 2015(18): 173-175.
-
[8]戚欣革. 配网运行管控中的营配调数据贯通研究[D]. 大连: 大连理工大学, 2018.
-
[9]李玮, 喻玮, 信博翔, 等. 基于图数据库配电网网架图谱校核的方法研究[J]. 电气自动化, 2021, 43(5): 37-40.
-
[10]全国电网运行与控制标准化技术委员会. 电网设备通用模型数据命名规范: GB/T 33601-2017[S]. 北京: 中国标准出版社, 2017: 5.
-
[11]余贻鑫, 栾文鹏. 智能电网述评[J]. 中国电机工程学报, 2009, 29(34): 1-8.
-
[12]栾文鹏, 余贻鑫, 王兵. AMI数据分析方法[J]. 中国电机工程学报, 2015, 35(1): 29-36.
-
[13]刘灏, 毕天姝, 周星, 等. 电力互感器对同步相量测量的影响[J]. 电网技术, 2011, 35(6): 176-182.
-
[14]林顺富, 詹银枫, 李毅, 等. 基于CNN-BiLSTM与DTW的非侵入式住宅负荷监测方法[J]. 电网技术, 2022, 46(5): 1973-1981.
-
[15]刘卓睿, 熊健豪, 曾清霖, 等. 基于DTW算法和遗传算法的三相不平衡负荷调整[J]. 江西电力, 2024, 48(1): 32-39.
-
[16]HU H L, ZHAO J, BIAN X Y, et al. Transformer-customer relationship identification for low-voltage distribution networks based on joint optimization of voltage silhouette coefficient and power loss coefficient[J]. Electric Power Systems Research, 2023, 216: 109070. DOI:10.1016/j.epsr.2022.109070