|
|
|
发布时间: 2024-04-28 |
特约专栏:新型源荷与配电网互动技术 |
|
|
|
收稿日期: 2023-09-17
中图法分类号: TM715;U496.72
文献标识码: A
文章编号: 2096-8299(2024)02-0109-06
|
摘要
针对现有电动汽车充电站规划研究鲜有考虑碳排放的问题,提出了一种电-路耦合网络下电动汽车充电站选址定容低碳规划的方法。首先,建立电-路耦合网络,考虑不同车辆的相互影响并计及电动汽车用户里程焦虑,利用蒙特卡洛法模拟车流;其次,对耦合网络碳排放进行溯源和追踪;然后,考虑经济成本和碳排放量,建立多目标充电站规划模型,并利用帕累托前沿求取最优解;最后,以IEEE 33节点配电网和12节点交通网组成的耦合网络作为算例,验证所提方法的有效性。
关键词
电动汽车; 充电站规划; 碳排放; 动态用户均衡原则; 耦合网络
Abstract
Aiming at the fact that carbon emission is rarely considered in the existing planning studies of electric vehicle charging station, a low carbon planning method for location and capacity of electric vehicle charging station under the electric⁃circuit coupling network is proposed. Firstly, an electric-circuit coupling network is established, and Monte Carlo is used to simulate traffic flow, considering the interaction of different vehicles and the range anxiety of EV users.Secondly, traceability and tracking is done of carbon emissions is conducted in the coupled network.Then, considering the economic cost and carbon emission, the multi-objective planning model of charging station is established and solved by Pareto frontier.Finally, the coupling network of IEEE 33⁃node distribution network and 12-node traffic network is analyzed as an example to verify the effectiveness of the proposed method.
Key words
electric vehicles; charging station planning; carbon emissions; dynamic user equilibrium; coupled network
全球温室气体排放总量的39%。因此,中国提出了碳达峰与碳中和目标指导交通系统与能源系统的低碳化发展[2]。
电动汽车是传统燃油车的环保替代品,推广电动汽车需要完善的充电设施网络,但现有的充电基础设施仍存在规划布局不合理等问题[3]。电力网络负荷和交通网络负荷是电动汽车应同时兼具的特性[4],合理规划充电站位置、适当改变充电负荷的空间分布是实现电力-交通(以下简称“电-路”)耦合网络低碳运行的关键问题。
在现有的电-路耦合网络的研究成果中,对于充电站规划问题主要考虑交通、电网、建设成本和用户出行规律等因素。文献[5]利用用户均衡原则构建网络耦合模型,建立了充电站多目标规划体系。文献[6-7]考虑电动汽车出行需求的不确定性,建立了随机静态交通分配模型进行充电站规划。但上述文献没有考虑燃油车与电动汽车的相互影响。文献[8]在充电站规划问题中考虑燃油车与电动汽车的动态混合交通流进行充电站规划。对于“双碳”目标发展视角下如何规划充电站才能降低网络碳排放量的研究仍处于起步阶段。文献[9]认为电动汽车的大规模充电行为会导致电网网损增加,电动汽车前往充电站距离过远也会间接增加碳排放。文献[10-11]将碳排放与碳交易市场相结合,利用碳排放售价衡量碳排放量的经济效益,以最大效益和最小成本为目标函数建立模型。文献[12]通过构建电动汽车充电与发电设备边际碳排放增长的时空模型计算发电设备碳排放量,并通过调节电动汽车有序充电来降低碳排放量。文献[13]在交通均衡模型中加入了碳排放约束,在多用户实现纳什均衡状态的同时尽可能减少碳排放,但其考虑的碳排放主体是燃油车,忽略了电动汽车及其他因素的碳排放。文献[14]将电动汽车聚合负荷转移至可再生能源发电节点,间接实现了全网低碳化,但并未考虑充电需求约束和用户的满意度。因此,为了使充电负荷的空间分布更加合理,在考虑电动汽车用户充电需求的前提下充分挖掘充电站位置的降碳潜力,利用合理的充电站位置引导电动汽车充电,改变充电负荷的时空分布特性,从而配合电-路耦合网络中原有的可再生能源发电,降低间接碳排放,实现网络低碳协同运行。
基于上述原因,本文提出了一种在电-路耦合网络中考虑碳排放的电动汽车充电站规划方法。首先,基于混合动态用户均衡原则,构建电路耦合网络模型,分析道路车流分布,进而得到充电需求的时空特性;其次,对耦合网络的碳排放进行溯源和追踪,并对网络中的碳排放量精确建模;然后,以充电站综合成本和碳排放量均最小为目标建立充电站规划模型,通过帕累托最优前沿分析选址结果,并结合排队理论确定充电站容量;最后,算例仿真结果表明,所提方法能够使充电站在满足充电需求的同时降低网络碳排放量。
1 电-路耦合网络模型
1.1 动态混合交通网络模型
混合交通网为GT={TN,TA},TN为节点集合,TA为道路集合,对于任意a∈TA表示2个相邻节点之间的道路。配电网为GD={DN,DA},其中DN和DA分别为配电网节点和线路的集合。出行节点由一组出发节点和目的节点组成,用OD表示,O为路径起点,D为路径结束点。
参考文献[15]中燃油车出行成本模型,电动汽车的路径选择成本包括行驶时间成本、能耗成本和里程焦虑成本。假设车辆类型中所有车辆同质,则有
| $ \begin{aligned} T_{{\mathrm{e}}}= & \min \int_0^{x_{a, t}} C_{{\mathrm{e}}, a}^\tau \tau_{a, t}(\omega) {\mathrm{d}} \omega+ \\ & \sum\limits_a\left(C_{{\mathrm{e}}, a}^{{\mathrm{n}}} n_{{\mathrm{e}}, a, t} x_{{\mathrm{e}}, a, t}\right)+C_{{\mathrm{j}}} R(l) \end{aligned} $ | (1) |
式中:Te——电动汽车路径选择成本;
xa,t——t时刻道路a上车辆总数;
Ce,aτ——行驶时间成本系数;
τa,t——路段行驶时间;
ω——路段行驶时间函数变量;
Ce,an——能耗成本系数;
ne,a,t——电动汽车的实时能耗;
xe,a,t——道路a上电动汽车数量;
Cj——里程焦虑成本系数;
R(l)——里程焦虑函数;
l——行驶里程。
里程焦虑函数R(l)的公式为
| $ R(l)= \begin{cases}0, & 0 \leqslant l \leqslant l_{{\text {comf }}} \\ \frac{R_{\max }\left(l-l_{{\text {comf }}}\right)^2}{\left(\frac{L}{\mu}-l_{{\text {comf }}}\right)^2}, & l_{{\text {comf }}} \leqslant l \leqslant \frac{L}{\mu}\end{cases} $ | (2) |
式中:lcomf——舒适里程阈值,取60 km;
Rmax——最大里程焦虑;
μ——线性参数;
L——续航里程,取200 km。
1.2 电-路耦合拓扑模型
交通网络中侧重于电动汽车的出行特征,配电网中侧重于其充电特性,建立电-路耦合拓扑模型为
| $ {\boldsymbol{W}}=\left[\begin{array}{cccc} \delta_{11} & \delta_{12} & \ldots & \delta_{1 A^{\prime}} \\ \delta_{21} & \delta_{22} & \ldots & \delta_{2 A^{\prime}} \\ \vdots & \vdots & & \vdots \\ \delta_{R^{\prime} 1} & \delta_{R 2} & \ldots & \delta_{R^{\prime} A^{\prime}} \end{array}\right] $ | (3) |
| $ {\boldsymbol{E}}_{{\mathrm{set}}}=\left[\begin{array}{llll} e_1 & e_2 & \ldots & e_N \end{array}\right] $ | (4) |
式中:W——交通网节点路段的关联矩阵;
δR'A'——节点与路段的位置关系,节点R′在路段A′首端则为1,末端为-1,无关为0;
Eset——配电网侧充电站待建节点矩阵;
eN——配电网节点与路段的交集关系,若有关则eN=1,否则eN=0;
N——充电站数量。
2 电-路耦合网络的碳排放追踪
2.1 交通网碳排放模型
燃油汽车行驶过程中会因消耗汽油直接产生碳排放,其碳排放量Etrans公式为
| $ E_{{\text {trans }}}=E_{{\text {gfactor }}} \sum\limits_O^D \sum\limits_a n_{{\mathrm{g}}, a, t} x_{{\mathrm{g}}, a, t} $ | (5) |
式中:Egfactor——燃油汽车碳排放因子;
ng,a,t——燃油汽车的实时能耗;
xg,a,t——道路a上燃油车数量。
2.2 配电网碳排放模型
(1)配电网网损产生的碳排放量Enet公式为
| $ E_{{\text {net }}}=\sum\limits_{d=1}^{365} \sum\limits_{h=1}^{24} \sum\limits_{m, n \in D_{{\mathrm{N}}}} I_{m n}^2 R_{m n} E_{{\text {factor }}} $ | (6) |
式中:d——天数,共365 d;
h——小时数,共24 h;
m,n——线路节点编号;
Imn——线路流经电流;
Rmn——线路电阻;
Efactor——区域电网年平均供电碳排放因子。
(2)电动汽车往返充电站的额外碳排放量Eev公式为
| $ E_{{\text {ev }}}=e_{{\text {factor }}} \sum\limits_{i \in N_{{\mathrm{cs}}}} \sum\limits_{j \in J} I_i p n_j d_{i j} $ |
式中:efactor——电动汽车单位行驶距离的碳排放系数;
Ncs——充电站集合;
J——充电需求点集合;
Ii——充电站i的状态变量;
p——充电需求点j的电动汽车充电概率;
nj——充电需求点j的电动汽车数量;
dij——充电需求点j到充电站i的距离。
(3)充电站接入点存在光伏发电时,充电功率中传统能源发电的等效碳排放量Ecs公式为
| $ E_{{\mathrm{cs}}}= \begin{cases}\frac{E_{{\text {factor }}}}{\eta_{{\mathrm{chg}}}} \int_{t_0}^t\left(P_{{\text {need }}}-P_{{\mathrm{PV}}}\right) {\mathrm{d}} t, & 0 \leqslant P_{{\mathrm{PV}}} \leqslant P_{{\text {need }}} \\ 0, & P_{{\mathrm{PV}}}>P_{{\text {need }}}\end{cases} $ | (8) |
式中:ηchg——充电站充电效率;
t0——电动汽车开始充电的时间;
Pneed——电动汽车所需充电量;
PPV——充电站光伏输出功率。
3 充电站选址定容规划模型
3.1 基于排队理论的定容模型
充电站的充电桩数量决定了电动汽车用户排队等待的时间。本文采用文献[16]中的排队模型计算电动汽车的平均等待时长,对充电站中的充电桩数量进行合理配置。假设充电站中共有c个充电桩,则用户进站充电的平均排队等待时间Wq为
| $ W_{{\mathrm{q}}}=\frac{(c \rho)^c \rho}{c!(1-\rho)^2 \lambda} P_0 $ | (9) |
式中:ρ——充电桩服务强度;
λ——每个充电桩单位时间内完成服务的车辆数;
P0——负指数分布概率。
3.2 目标函数
建立一个综合考虑充电站建设维护成本、电动汽车用户排队成本和电-路耦合网络碳排放的多目标规划模型为
| $ \left\{\begin{array}{l} \min C=C_{{\mathrm{c}}}+C_{{\mathrm{w}}}+C_{{\mathrm{t}}} W_{{\mathrm{q}}} \\ \min E=E_{{\text {tans }}}+E_{{\mathrm{net}}}+E_{{\mathrm{ev}}}+E_{{\mathrm{cs}}} \end{array}\right. $ | (10) |
式中:C——充电站综合总成本;
Cc——充电站建设成本;
Cw——充电站维护成本;
Ct——时间成本系数;
E——耦合网络碳排放量。
充电站建设成本Cc的公式为
| $ C_{{\mathrm{c}}}=\sum\limits_{i=1}^N\left(C_{{\mathrm{tz}}}+C_{{\mathrm{cdz}} } N_i^d\right) \frac{r_0\left(1+r_0\right)^k}{\left(1+r_0\right)^k-1} $ | (11) |
式中:Ctz——充电站的投资成本;
Ccdz——单个充电桩的价格;
Ndi——第i座充电站充电桩数量;
r0——贴现率;
k——运行年限。
充电站维护成本Cw的公式为
| $ C_{{\mathrm{w}}}=T_{{\mathrm{n}}} \sum\limits_{i=1}^N\left[(\alpha+\beta) T_{{\mathrm{cdz}}} N_i^d\right] P_{{\mathrm{cdz}} } $ | (12) |
式中:Tn——充电站一年的维护成本参数;
α——人工费用比例系数;
β——并网成本比例系数;
Tcdz——充电桩日平均运行时间;
Pcdz——充电桩功率。
3.3 约束条件
(1)潮流约束条件为
| $ \left\{\begin{array}{l} P_{i {\mathrm{~s}}}=U_i \sum\limits_{j \in i} U_i\left(G_{i j} \cos \theta_{i j}+B_{i j} \sin \theta_{i j}\right) \\ Q_{i {\mathrm{~s}}}=U_i \sum\limits_{j \in i} U_i\left(G_{i j} \sin \theta_{i j}-B_{i j} \cos \theta_{i j}\right) \end{array}\right. $ | (13) |
式中:Pis——节点i的有功注入;
Qis——节点i的无功注入;
Ui——节点i的电压幅值;
Gij——节点导纳矩阵的实部;
Bij——节点导纳矩阵的虚部;
θij——节点i和节点j之间的相角差。
(2)配电网允许接入的电动汽车最大充电功率约束条件为
| $ \sum\limits_{i=1}^N P_{{\mathrm{CS}} i} \leqslant P_{{\mathrm{C}}}^{\max } $ | (14) |
式中:PCSi——充电站i的充电功率;
PCmax——配电网允许接入的电动汽车最大充电功率。
(3)充电站接入点容量约束条件为
| $ P_{{\mathrm{CS}} i j} \leqslant P_{j \max } $ | (15) |
式中:PCSij——接入电网节点j处充电站i的最大充电功率;
Pjmax——电网节点j所能允许的最大接入功率。
3.4 求解算法
本文利用帕累托前沿求取最优解。考虑到实际充电站规划建设主要以盈利为主,本文根据经济成本优先原则对备选方案集中的个体进行排序,并确定最优方案。
4 算例分析
4.1 算例说明
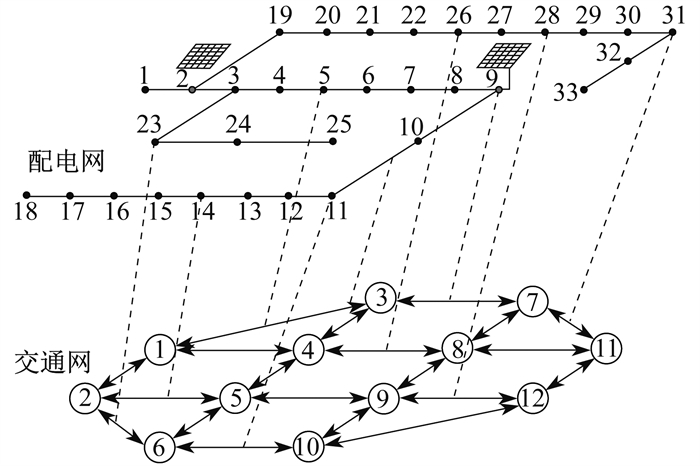
本文基于交通网络12节点及配电网IEEE33节点进行耦合建模。网络结构如图 1所示。其中,配电网节点2和节点9为光伏接入点,道路网络共有20条路段。
交通网络路段编号如表 1所示。
表 1
交通网络路段编号
| 路段号 | 起止点 | 路段号 | 起止点 | 路段号 | 起止点 | 路段号 | 起止点 | |||
| 1 | 1—3 | 6 | 5—6 | 11 | 5—9 | 16 | 10—12 | |||
| 2 | 1—2 | 7 | 4—5 | 12 | 6—10 | 17 | 9—12 | |||
| 3 | 2—6 | 8 | 3—4 | 13 | 7—8 | 18 | 8—11 | |||
| 4 | 2—5 | 9 | 3—7 | 14 | 8—9 | 19 | 7—11 | |||
| 5 | 1—4 | 10 | 4—8 | 15 | 9—10 | 20 | 11—12 |
车辆能耗参数参考文献[8]。假设任意充电站在同一时刻充电容量不超过200 kW,且选取7 kW的慢充充电桩进行规划配置。其他参数设置如下:Ccdz=1 000元/个,Ctz=100万元/座,α=2%,β=0.007,Tcdz=16 h,r0=3%,k=20 a。
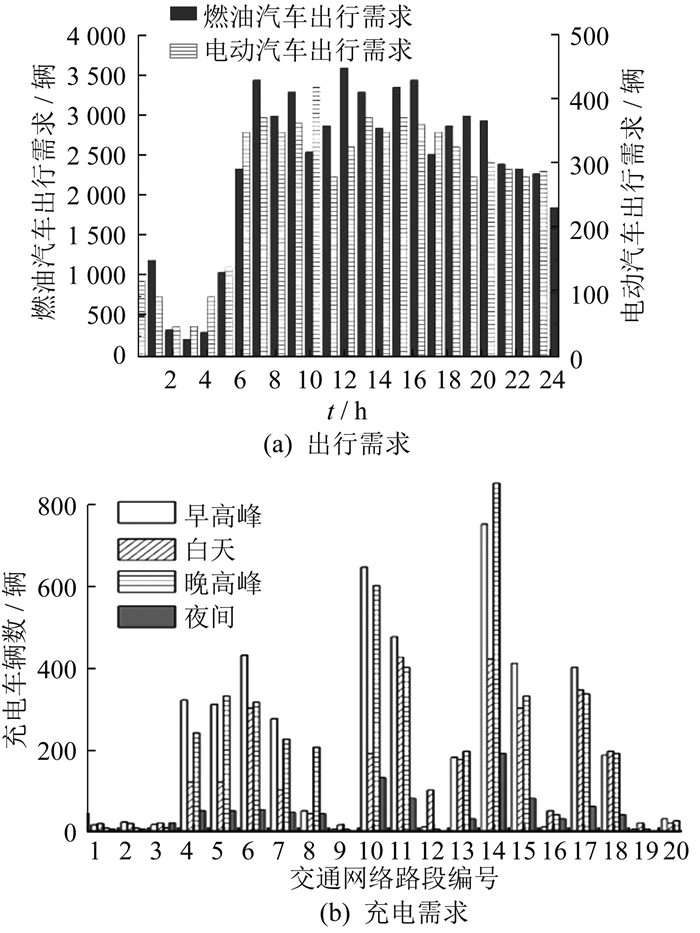
4.2 电动汽车充电需求分布
4.3 规划结果分析
根据帕累托前沿求取最优解,区域建设8~12座充电站能够满足实际目标要求,充电站的各项成本和建成后的碳排放量如表 2所示。
表 2
不同充电站数量下充电站的各项成本和碳排放量
| 充电站数量N/座 | 建设成本Cc | 维护成本Cw | 排队成本CtWq | 综合总成本C | 碳排放量E/万t |
| 万元 | |||||
| 8 | 85.68 | 148.36 | 436.12 | 670.16 | 31.02 |
| 9 | 87.54 | 165.25 | 428.63 | 681.42 | 29.36 |
| 10 | 89.15 | 174.36 | 410.36 | 673.87 | 25.48 |
| 11 | 103.87 | 215.93 | 384.24 | 704.04 | 24.57 |
| 12 | 120.42 | 230.78 | 345.85 | 697.05 | 23.19 |
由表 2可以看出,随着充电站数量的增加,充电站建设成本和维护成本不断增加,但用户排队成本和碳排放量在不断下降。当充电站数量为10座时,充电站综合总成本最低,且碳排放量相对较低。充电站选址定容结果如表 3所示。
表 3
充电站选址定容结果
| 充电站编号 | 所在节点 | 充电桩数量/个 | 充电站编号 | 所在节点 | 充电桩数量/个 |
| 1 | 2 | 18 | 6 | 21 | 24 |
| 2 | 5 | 27 | 7 | 25 | 20 |
| 3 | 6 | 25 | 8 | 26 | 16 |
| 4 | 19 | 24 | 9 | 27 | 20 |
| 5 | 20 | 17 | 10 | 31 | 18 |
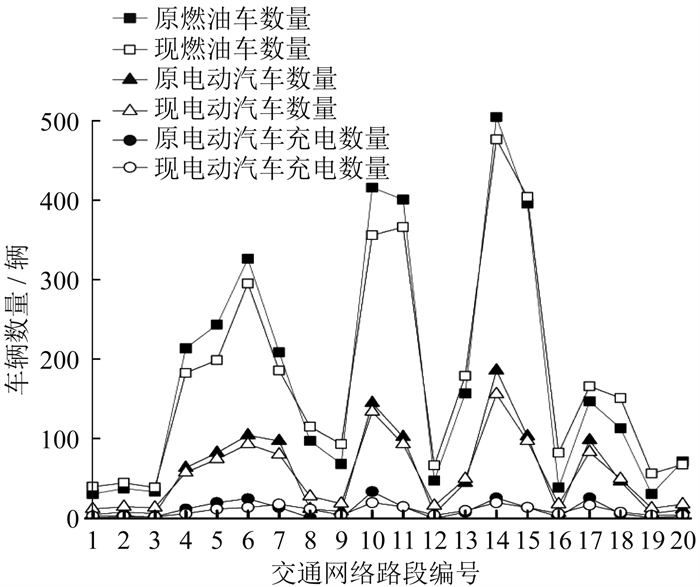
确定充电站规划方案后,将规划前后早高峰交通网络车流分布和电动汽车充电负荷的分布情况进行对比,如图 3所示。
由图 3可以看出,对于车流量较大的路段,规划后道路的行驶状况得到较为明显的改善。这是因为本文利用充电站的空间分布引导了电动汽车的充电决策和行驶路径,通过改变充电站位置将车辆引流至其他路段,改善了车流分布情况。电动汽车的充电负荷变得更加均衡,缓解了电动汽车用户里程焦虑,降低了充电引起的网络损耗。
本文考虑用户里程焦虑和网络碳排放对充电站进行规划,不同规划方案的结果对比如表 4所示。
表 4
不同规划方案结果对比
| 方法 | 是否考虑里程焦虑 | 是否考虑碳排放 | 充电站数量N/座 | 综合总成本C/万元 | 里程焦虑成本CjR(l)/万元 | 碳排放量E/万t |
| 1 | 是 | 是 | 10 | 673.87 | 24.26 | 25.48 |
| 2 | 是 | 否 | 8 | 664.25 | 38.47 | 33.85 |
| 3 | 否 | 否 | 7 | 662.48 | 42.98 | 36.74 |
由表 4可以看出:与方法1相比,方法2的充电站数量减少,综合总成本降低,用户里程焦虑成本和碳排放量增加,这是因为仅以降低成本为目的时,减少充电站数量使得电动汽车充电选择受限,增加了用户里程焦虑的同时影响了道路交通网络车流分布,从而增加了耦合网络的碳排放量。与方法2相比,方法3的里程焦虑成本上升,碳排放量最大。由此可知,本文规划方案综合考虑成本、用户和碳排放量,虽然综合总成本随充电站数量的增加而提高,但在缓解用户焦虑、改善交通流、降低耦合网络的碳排放量方面效果明显,证明了方案的有效性。
5 结语
本文针对电-路耦合网络充电站低碳规划问题,引入电动汽车用户里程焦虑建立混合动态用户均衡模型。算例结果表明,该方案更符合实际交通道路网络出行需求和车流分布情况,在分析电动汽车充电出行习惯时能够更加准确地获取其充电需求分布。对比不同方法可知,本文所提规划方案在降低综合成本的同时,能够减少耦合网络碳排放,针对当前双碳目标下的充电站规划有一定的参考价值。
参考文献
-
[1]United States Environmental Protection Agency. Global greenhouse gas emissions data[EB/OL]. (2022-02-25)[2022-08-18]. https://www.epa.gov/ghgemissions/globalgreenhouse-gas-emissions-data.
-
[2]中华人民共和国国务院新闻办公室. 《新时代的中国能源发展》白皮书[EB/OL]. (2020-12-21)[2022-08-18]. https://www.gov.cn/zhengce/2020-12/21/content_5571916.htm.
-
[3]王震坡, 张瑾, 刘鹏, 等. 电动汽车充电站规划研究综述[J]. 中国公路学报, 2022, 35(12): 230-252.
-
[4]袁泉, 汤奕. 基于路-电耦合网络的电动汽车需求响应技术[J]. 中国电机工程学报, 2021, 41(5): 1627-1636.
-
[5]王守相, 刘栋, 于潞, 等. 考虑交通网与配电网耦合基于数据包络分析的电动汽车充电设施多阶段规划方法[J]. 电力自动化设备, 2022, 42(10): 100-106.
-
[6]WU F, SIOSHANSI R. A stochastic flow-capturing model to optimize the location of fast-charging stations with uncertain electric vehicle flows[J]. Transportation Research Part D: Transport and Environment, 2017, 53(4): 354-376.
-
[7]WANG S, DONG Z Y, LUO F J, et al. Stochastic collaborative planning of electric vehicle charging stations and power distribution system[J]. IEEE Transactions on Industrial Informatics, 2018, 14(1): 321-331. DOI:10.1109/TII.2017.2662711
-
[8]卢慧, 谢开贵, 邵常政, 等. 考虑燃油车和电动汽车动态混合交通流的电动汽车充电站规划[J]. 高电压技术, 2023, 49(3): 1150-1160.
-
[9]陈光, 毛召磊, 李济沅, 等. 计及碳排放的电动汽车充电站多目标规划[J]. 电力系统自动化, 2014, 38(17): 49-53.
-
[10]叶宇静, 邢海军, 米阳, 等. 考虑低碳需求响应及主从博弈的综合能源系统低碳优化调度[J/OL]. 电力系统自动化, 2023: 1-17[2023-09-16]. http://h-p.kns.cnki.net.shiep.vpn358.com/kcms/detail/32.1180.TP.20230824.1932.008.html.
-
[11]尚楠, 冷媛, 陈政, 等. 考虑现货电能量交易的发用电主体碳排放权交易决策模型[J]. 电力系统自动化, 2023, 47(21): 36-46.
-
[12]程宏波, 肖永乐, 王勋, 等. 考虑低碳收益的电动汽车充电站选址规划[J]. 中国电力, 2016, 49(7): 118-121.
-
[13]李浩, 陈浩, 陆续, 等. 考虑排放约束的电动汽车混行交通路网均衡模型[J]. 交通运输工程与信息学报, 2021, 19(4): 24-35.
-
[14]LIU D N, WANG L X, WANG W Y, et al. Strategy of large-scale electric vehicles absorbing renewable energy abandoned electricity based on master-slave game[J]. IEEE Access, 2021, 9: 92473-92482. DOI:10.1109/ACCESS.2021.3091725
-
[15]张翀宇. 考虑充电选择行为和里程焦虑的电动汽车充电站选址模型研究[D]. 长春: 吉林大学, 2021.
-
[16]李浩, 陈浩. 考虑充电排队时间的电动汽车混合交通路网均衡[J]. 吉林大学学报(工学版), 2021, 51(5): 1684-1691.