|
|
|
发布时间: 2024-04-28 |
特约专栏:新型源荷与配电网互动技术 |
|
|
|
收稿日期: 2023-05-30
基金项目: 国家自然科学基金(52177098);上海绿色能源并网工程技术研究中心资助项目(13DZ2251900)
中图法分类号: TM732
文献标识码: A
文章编号: 2096-8299(2024)02-0115-09
|
摘要
为了促进电动汽车产业的进一步发展,构建了计及充换储一体站(CSSIS)的交直流混合配电网多时间尺度优化调度模型。首先,基于快充用户行为和城市交通特征分别构建了充电站模型和换电站模型,再结合储能电站模型完成了CSSIS建模。然后,在计及CSSIS、微型燃气轮机和可再生新能源等接入的交直流混合配电网中,构建了优化调度模型。为降低预测精度误差的影响,采用了多时间尺度协调优化策略处理。该模型属于非线性非凸混合整数规划问题,采用线性化和二阶锥松弛方法将其转化为可用商业求解器处理的混合整数二阶锥凸优化模型。最后,以改进的IEEE 50节点系统为例进行了仿真分析,仿真结果验证了交直流混合配电网形式具有更强的适应性,以及CSSIS具有高效参与电网优化运行的能力。
关键词
充换储一体站; 交直流混合配电网; 多时间尺度优化; 混合整数规划; 二阶锥优化
Abstract
In order to promote the further development of the electric vehicle industry, this article constructs a multi-time scale optimization dispatching model for AC/DC hybrid distribution networks that takes into account charging-swapping-storage integrated station(CSSIS).Firstly, a battery charging station model is established based on the behavior of fast charging users, followed by a battery swapping station model based on urban traffic characteristics. And then, a CSSIS model is completed by combining a energy storage station model.An optimized scheduling model is constructed in the AC/DC hybrid distribution network that takes into account CSSIS, microturbines and renewable energy sourse components. To reduce the impact of prediction accuracy errors, a multi time scale coordinated optimization strategy is adopted for processing.The model is a nonlinear nonconvex mixed integer programming problem.The linearization and secondorder cone relaxation methods are considered to transform it into a mixed integer second-order cone convex optimization model that can be processed by a commercial solver. Finally, an improved 50 node system is examplified for simulation analysis to verify that the AC/DC hybrid distribution network has stronger adaptability and CSSIS has the ability to efficiently participate in the optimization operation of the power grid.
Key words
charging-swapping-storage integrated station; AC/DC hybrid network; multi time scale optimization; mixed integer programming; second⁃order cone optimization
2022年底我国光伏(Photovoltaic,PV)和风电装机规模分别达到3.92亿kW和3.65亿kW,可再生能源(Renewable Energy Source,RES)规模得到较快增长。与此同时,电动汽车(Electric Vehicle,EV)技术快速发展,EV充电需求量已逐渐成为电网部分时段的主要用电负荷。随着电力系统源-荷组成部分发生革命性变化,传统的交流供电形式面临新的挑战。RES和EV等直流电源和负荷需要通过整流及逆变等环节才能接入交流配电网,在此过程中会产生较多的逆变器损耗,增加系统损耗[1]。与传统的交流配电网不同,新型的直流配电形式对PV等直流电源和EV等直流负荷具有更强的适应性,可进一步增强新元件接入电力系统后运行的可靠性[2]。在此基础上,基于电力电子技术实现交直流混合互联的交直流混合配电网,由于兼具二者的优势,因此将会在未来成为配电网络的主要形态[3]。但是相关文献侧重于对其自身运行控制策略[4]、组成电网架构[5]和供电能力进行研究,对计及RES和EV等新元件接入的优化运行问题涉及相对较少[6]。
随着“双碳”目标下交通领域电气化进程的加快,EV充换电设施相对不足已逐渐成为制约EV产业进一步发展的主要瓶颈。与较为传统的EV分散式充、换电模式不同[7-8],EV充换储一体站(Charging-Swapping-Storage Integrated Station,CSSIS)通过把充电站(Battery Charging Station,BCS)、换电站(Battery Swapping Station,BSS)和储能电站(Energy Storage Station,ESS)集成一体,可提高系统综合利用率[9],充分发挥集约优势来节约用地[10],提升电池利用率[11]和改善电力系统电压控制能力[12],发展前景广阔。但是目前相关研究主要集中于分析传统运行模型[13],并未涉及交直流混合配电网等新型配电形式的运行。
针对上述情况,本文提出了一种计及CSSIS的交直流混合配电网多时间尺度优化调度模型。首先,基于EV快充用户日常行驶行为特征、电动公交车城市道路交通实用模型和ESS运行特性,构建了具备调度潜力的CSSIS数学模型;然后,在计及CSSIS、微型燃气轮机(Micro⁃Turbine,MT)和RES等接入的交直流混合配电网中,提出了一种以配电网日总成本最小为目标的多时间尺度优化调度模型,采用凸松弛技术将其转化为可用商业求解器高效求解的二阶锥规划模型;最后,以改进的IEEE 50节点系统为例进行仿真验证。
1 CSSIS数学模型构建
1.1 整体模型
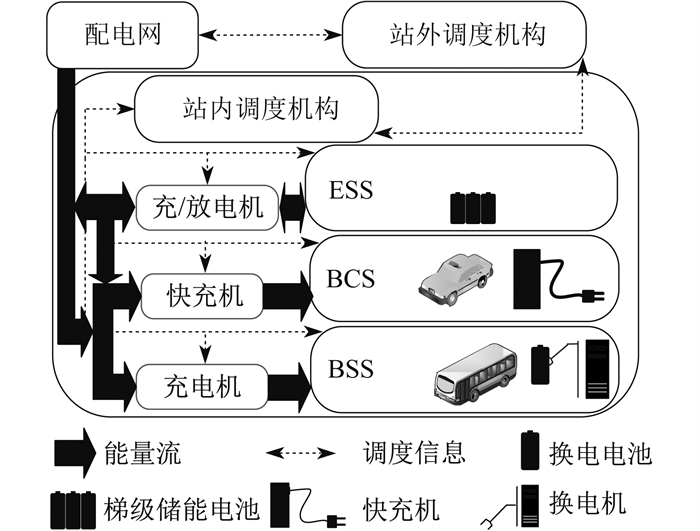
CSSIS由调度机构、BCS、BSS和ESS构成,组成结构如图 1所示。
其中,调度机构包括站内调度机构和站外调度机构两部分。前者是CSSIS内部的功率能量信息整合中心,负责对站内的信息流、功率流和能量流进行实时监控并上传给电网层面的站外调度机构,同时接受其相应的调度,调整站内充换电方案。第t时段CSSIS充放电功率PCSSIS(t)为
| PCSSIS (t)=PBCS (t)+PBSS (t)+PESS (t) | (1) |
式中:PBCS(t)——第t时段BCS的充电功率;
PBSS(t)——第t时段BSS的充电功率;
PESS(t)——第t时段ESS的总充放电功率。
1.2 BCS运行模型
1.2.1 EV快充用户泊松分布模型
目前主要快充用户是电动出租车(Electric Taxi,ET),其到达过程服从泊松分布。除ET之外,部分电动商务车及电动私家车等也是快充用户,其充电时刻暂无明显规律,到达过程也服从泊松分布。因此,根据EV快充用户日常行驶行为特征,考虑采用排队论对其充电过程进行建模[14]。
快充用户到达过程服从参数为λ的泊松分布,充电时间服从正态分布G,假定快充用户充电时长为T0,则模型表述为
| T0=BcapBCS−BBCS(i)PNc,BCS | (2) |
| ET=BcapBCS−E[BBCS(i)]PNc, BCS | (3) |
| DT=D[BBCS(i)](PNc,BCS)2 | (4) |
式中:BBCScap——快充用户电池能量;
BBCS(i)——抵达BCS时第i个快充用户能量;
Pc,BCSN——快充机额定充电功率;
ET——充电时间期望;
E(·)——期望函数;
DT——充电时间方差;
D(·)——方差函数。
ET用户泊松分布参数和其他快充用户的概率密度函数分别可由如下公式求出:
| λET=NETTET | (5) |
| f(Xt=K)=(λt)Ke−λtK! | (6) |
式中:λET——ET用户泊松分布参数;
NET——服务区域内ET数量;
TET——ET白班和夜班交接时长;
f(·)——概率密度函数;
Xt——第t时段其他快充用户抵达数量;
K——其他快充用户数量;
λt——第t时段到达率。
1.2.2 BCS充电模型
第t时段BCS内的充电功率PBCS(t)为
| PBCS(t)=NcBCS(t)PNc,BCS | (7) |
| 0⩽NcBCS(t)⩽NBCS | (8) |
式中:NBCSc(t)——第t时段快充用户数量;
NBCS——BCS的充电桩数量。
1.3 BSS运行模型
1.3.1 道路交通实用模型
本文针对EV车流量和平均车速进行精确建模,引入的道路交通实用模型[15]为
| {vks(t)=v0ks1+[Sks(t)]ββ=a+b[Sks(t)]rSks(t)=qks(t)Cks | (9) |
式中:vks(t),vks0——第t时段始末端点分别为k和s的直连路段(k,s)行驶速率、零流速率;
Sks(t)——第t时段直连路段(k,s)饱和度;
a,b,r——不同直连路段下参数值;
qks(t)——第t时段直连路段(k,s)流量;
Cks——直连路段(k,s)通行度。
1.3.2 BSS换电模型
BSS为城市内部的电动公交车(Electric Bus,EB)提供充换电服务,其充电功率PBSS(t)为
| PBSS(t)=NswapBSS(t)PNc,BSS | (10) |
| 0⩽Nswap BSS (t)⩽NBSS | (11) |
式中:NBSSswap(t)——第t时段BSS充电状态下电池数量;
Pc,BSSN——BSS换电站充电桩额定功率;
NBSS——BSS的充电桩数量。
行驶状态下第i辆EB功率损耗PEBi(t)[16]为
| PiEB(t)=1ηT[mgfˉv(t)3600+CDA¯v3v(t)76140] | (12) |
式中:ηT——传动机效率;
m——EB的重量;
g——重力加速度;
f——特定路段阻力综合系数;
v(t)——第t时段EB根据道路交通实用模型获取的路段平均行驶速率;
CD——风阻系数;
A——迎风系数。
第t时段BSS能量状态值EBSS(t)为
| EEBi, cap (t)=PiEB(t)⋅diEB(t) | (13) |
| EEBcap (t)=NEBBSS∑i=1EEBi, cap (t) | (14) |
| EBSS(t)=EBSS(t−1)+PBSS(t−1)ΔT−EEBcap(t−1) | (15) |
式中:Ei,capEB(t)——第t时段第i辆EB行驶能耗;
dEBi(t)——第t时段第i辆EB行驶路程;
EcapEB(t)——第t时段EB总行驶能耗;
NBSSEB——BSS中EB的总数;
ΔT——时间间隔。
1.4 ESS运行模型
ESS充放电模型为
| PESS(t)=PESS,c(t)ηcESS−PESS,d(t)ηdESS | (16) |
| 0⩽PESS,c(t)⩽PNESSωc(t) | (17) |
| 0⩽PESS,d(t)⩽PNESSωd(t) | (18) |
| ωc(t)+ωd(t)⩽1 | (19) |
| EESS(t)=EESS(t−1)+PESS(t)ΔT | (20) |
| EESSmin | (21) |
式中:PESS,c(t),PESS,d(t)——第t时段ESS充、放电功率;
ηESSc,ηESSd——ESS充、放电效率;
PESSN——ESS额定功率;
ωc(t),ωd(t)——表征充、放电状态的二进制变量,取1时表明处于充、放电状态,反之取0;
EESS(t)——第t时段ESS能量值;
EESSmax,EESSmin——ESS储能容量上下限。
2 交直流混合配电网元件特性模型构建
2.1 MT特性模型
MT作为灵活性强的调峰电源,其实际输出功率PMT(t)需小于机组最大输出功率PMTmax,同时需满足爬坡约束条件[21]:
| 0 \leqslant P_{{{\mathrm{MT}}}}(t) \leqslant P_{{{\mathrm{MT}}}}^{\max } | (22) |
| \Delta P_{{{\mathrm{MT}}}}^{\min } \leqslant P_{{{\mathrm{MT}}}}(t)-P_{{{\mathrm{MT}}}}(t-1) \leqslant \Delta P_{{{\mathrm{MT}}}}^{\max } | (23) |
式中:ΔPMTmax,ΔPMTmin——MT爬坡约束上下限值。
2.2 RES特性模型
作为不可控可再生能源元件,风机(Wind Turbine,WT)、PV系统第t时段的实际输出功率值PWT(t)和PPV(t)需要小于其最大输出功率预测值PWTmax(t)和PPVmax(t)。
| \left\{\begin{array}{l} P_{{{\mathrm{WT}}}}(t) \leqslant P_{{{\mathrm{WT}}}}^{\max }(t) \\ P_{{{\mathrm{PV}}}}(t) \leqslant P_{{{\mathrm{PV}}}}^{\max }(t) \end{array}\right. | (24) |
2.3 BSS特性模型
本文考虑BSS的用户主要为EB,其充电行为采用有序充电模式,即根据EB实际运营情况获取实时路况等信息,同时上传给区域内统一的调度中心,并依据其调度指令分配EB充电行为,因此换电模式具有参与电网优化运行的能力。为挖掘BSS参与电网调度运行的潜力,定义以下状态量。
起始有效充电时间主要受到EB进站、换电时间和运行模式的约束,其表述为
| t_{{{\mathrm{BSS}}}}^{i, {{\text { beg }}}}=\left\lceil t_{i, {{\mathrm{~EB}}}}^{{{\text {in }}}}+t_{i, {{\text { swap }}}}\right\rceil | (25) |
式中:ti,EBin,ti,swap——第i辆EB进站、换电时间;
「.⌉——向上取整。
充电允许截止时间tBSSi, end为
| t_{{{\mathrm{BSS}}}}^{i, {{\text { end }}}}=\left\lfloor t_{i, {{\mathrm{~EB}}}}^{{{\text {out }}}}-t_{i, {{\text { swap }}}}\right\rfloor |
式中:ti,EBout——第i辆EB营运计划发车时间;
⌊.」——向下取整。
对EB电池能量状态离散化处理可获得单位时段电池能量增量ΔEBSSswap,从而可得出充电必要时间tiBSS为
| \Delta E_{{{\mathrm{BSS}}}}^{{{\mathrm{swap}}}}=\frac{P_{{{\mathrm{c}}}, {{\mathrm{BSS}}}}^{{{\mathrm{N}}}}}{B_{{{\mathrm{cap}}}}^{{{\text {bus }}}}} | (27) |
| t_{{{\mathrm{BSS}}}}^i=\left\lceil\frac{1-E_{{{\mathrm{bus}}}}^i\left(t_{i, {{\mathrm{~EB}}}}^{{{\text {in }}}}\right) / B_{{{\mathrm{cap}}}}^{{{\text {bus }}}}}{\Delta E_{{{\mathrm{BSS}}}}^{{{\text {swap }}}}}\right] | (28) |
式中:Bcapbus——每辆EB电池能量值;
Ebusi(ti,EBin)——第ti,EBin时段进站的第i辆EB的电池能量。
考虑对BSS具备的调度能力进行刻画,引入充电启动状态变量yi(t)和切换状态变量zi(t)二者均为二进制变量。yi(t)取1表示第t时段对第i辆EB的电池启动充电,否则取0;zi(t)取1表示第t时段对第i辆EB的电池充电状态进行切换,否则取0。
| \left\{\begin{array}{l} y_i(t)=\max \left[0, \omega_{i, {{\mathrm{BSS}}}}^{{{\mathrm{swap}}}}(t)-\omega_{i, {{\mathrm{BSS}}}}^{{{\mathrm{swap}}}}(t-1)\right] \\ z_i(t)=\left|\omega_{i, {{\mathrm{BSS}}}}^{{{\mathrm{swap}}}}(t)-\omega_{i, {{\mathrm{BSS}}}}^{{{\mathrm{swap}}}}(t-1)\right| \end{array}\right. | (29) |
式中:ωi, BSSswap(t)——二进制变量,表示第t时段BSS中第i辆EB的电池充电状态。
可以看出,第i辆EB的电池实际起始充电时间ti,acbeg在[tBSSi, beg,tBSSi,end-tiBSS]区间,实际终止充电时间tendi,ac在[tBSSi, beg+tBSSi,tBSSi,end]区间。BSS具备的可调能力建模为
| \left\{ {\begin{array}{*{20}{l}} {\sum\limits_{t = t_{{\rm{BSS}}}^{i,beg}}^{t_{{\rm{BSS}}}^{i,{\rm{end}}}} {\omega _{i,{\rm{BSS}}}^{{\rm{swap}}}\left( t \right) - t_{{\rm{BSS}}}^i{y_i}\left( t \right) = 0} }\\ {\sum\limits_{t = t_{{\rm{BSS}}}^{i,beg}}^{t_{{\rm{BSS}}}^{i,{\rm{end}}} - t_{{\rm{BSS}}}^i} {{y_i}\left( t \right) = 1} }\\ {\sum\limits_{t = t_{{\rm{BSS}}}^{i,{\rm{end}}} + t_{{\rm{BSS}}}^i}^{t_{{\rm{BSS}}}^{i,{\rm{end}}}} {{y_i}\left( t \right) = 0} }\\ {\sum\limits_{t = t_{{\rm{BSS}}}^{i,beg}}^{t_{{\rm{BSS}}}^{i,{\rm{end}}}} {{z_i}\left( t \right)} = 2} \end{array}} \right. | (30) |
3 配电网优化调度模型构建
3.1 日前优化调度模型
本文提出的计及CSSIS的交直流混合配电网日前优化调度模型,以配电网日总综合成本F最小为目标:
| \min F=F_{{\text {oper }}}+F_{{\mathrm{CO}}_2} | (31) |
式中:Foper,FCO2——交直流混合配电网日运行成本和日碳排放成本。
配电网日运行成本Foper主要包括:与上级主网的基本负荷日购电成本Fpur,MT日运行成本FMT,ESS日调度成本FESS,配电网日损耗成本Floss,公式为
| F_{{\text {oper }}}=F_{{\text {pur }}}+F_{{\mathrm{MT}}}+F_{{\mathrm{ESS}}}+F_{{\text {loss }}} | (32) |
基本负荷日购电成本Fpur为
| F_{{\mathrm{pur}}}=\sum\limits_{t=1}^T c_{{\mathrm{pur}}}(t) P_{{\mathrm{pur}}}^{{\text {load }}}(t) \Delta T | (33) |
式中:cpur(t)——第t时段电价;
Ppurload(t)——第t时段配电网基本负荷需求。
MT日运行成本FMT为
| F_{{\mathrm{MT}}}=\sum\limits_{t=1}^T \sum\limits_{j=1}^N\left[c P_{{\mathrm{MT}}, j}^2(t)+d P_{{\mathrm{MT}}, j}(t)+e\right] | (34) |
式中:N——规划区域MT总数;
T——总时段数;
PMT,j(t)——第t时段节点j的MT实际输出功率;
c,d,e——MT运行成本系数。
ESS日调度成本FESS为
| F_{{\mathrm{ESS}}}=\sum\limits_{t=1}^T c_{{\mathrm{ESS}}}\left[P_{{\mathrm{ESS}}}(t) \Delta T\right]^2 | (35) |
式中:cESS——ESS调度成本系数[20]。
配电网日损耗成本Floss为
| \begin{gathered} F_{{\text {loss }}}=\sum\limits_{t=1}^T c_{{\text {pur }}}(t) R_{m n}\left[\frac{P_{m n}^2(t)+Q_{m n}^2(t)}{U_m^2(t)}\right] \\ \forall m 、n \in \varOmega_{{\text {net }}} \end{gathered} | (36) |
式中:Rmn——节点m和节点n之间的支路m-n电阻;
Pmn(t),Qmn(t)——第t时段支路m-n的有功、无功潮流;
Ωnet——配电网网络节点集合。
配电网日碳排放成本FCO2主要由从上级主网购电产生的碳排放成本FCO2pur和由MT出力产生的碳排放成本FCO2MT两部分组成。
| F_{{\mathrm{CO}}_2}=F_{{\mathrm{CO}}_2}^{{\mathrm{pur}}}+F_{{\mathrm{CO}}_2}^{{\mathrm{MT}}} | (37) |
| F_{{\mathrm{CO}}_2}^{{\mathrm{pur}}}=c_{{\mathrm{CO}}_2}\left\{\sum\limits_{=1}^T \alpha^{{\mathrm{c}}}\left[P_{{\text {pur }}}(t) \Delta T\right]^2+\beta^{{\mathrm{c}}} P_{{\text {pur }}}(t) \Delta T\right\} | (38) |
| F_{{\mathrm{CO}}_2}^{{\mathrm{MT}}}=c_{{\mathrm{CO}}_2} \sum\limits_{t=1}^T \sum\limits_{j=1}^N\left[\mu_{{\mathrm{MT}}}^1 P_{{\mathrm{MT}}, j}^2(t)+\mu_{{\mathrm{MT}}}^2 P_{{\mathrm{MT}}, j}(t)\right] | (39) |
式中:cCO2——政府批复碳价格;
αc,βc——煤电排放系数;
Ppur(t)——第t时段配电网与主网交互功率值;
μMT1,μMT2——MT碳排放价格系数。
3.2 多时间尺度优化调度模型
上文中的优化模型是在日前时间尺度下开展的运行分析过程中建立的。由于在实际运行时RES输出功率和负荷需求预测存在不确定性,因此需要开展多时间尺度下的协调优化[22]。
3.2.1 日内优化调度
为了缓解由于日前预测误差导致的实际运行情况偏差,所以日内优化调度的时间尺度采用5 min为步长滚动进行。日内优化调度目标为在考虑不确定性影响下配电网与主网交互功率波动程度Finday最小。
由于BSS的有序充电安排在日前已经确定,日内将不再进行变动,因此本阶段的控制变量主要为WT、PV、MT、ESS的输出功率,其目标函数如下:
| min F_{{\text {in-day }}}=\sum\left|P_{{\text {pur }}}^{{\text {inday }}}(t+h \mid t)-P_{{\text {pur }}}(t+h)\right| \Delta T | (40) |
式中:Ppurinday(t+h|t)——第t时段预测的未来t+h时段配电网与主网交互功率值;
Ppur(t+h)——第t+h时段配电网与主网交互功率参考值,可由日前时间尺度下的优化调度模型求得。
3.2.2 实时反馈
由于日内优化调度阶段实质仍属于开环优化,因此将无法保证RES实际输出功率和负荷需求实际值与日内预测值相同。通过在模型中增加实时反馈环节,可以显著缓解因预测精度造成的误差对计算的影响,提高控制变量和交互功率预测精度。
| P_{{\text {pur }}}^{{\text {inday, }} 0}(t+1)=P_{{\text {pur }}}^{{\text {inday, real }}}(t+1) | (41) |
式中:Ppurinday,0(t+1)——第t+1时段控制变量输出功率与配电网和主网交互功率初始值;
Ppurinday,real(t+1)——调度中心在将控制变量第t时段输出功率变化值下发后,实际测量到的控制变量输出功率与配电网和主网交互功率值。
3.3 约束条件
本文构建的交直流配电网优化调度模型约束主要包括:交流和直流配电网支路潮流约束、电压源换流器(Voltage Source Converter,VSC)换流站运行约束,以及配电网安全运行约束。
3.3.1 交流配电网支路潮流约束
实际应用中配电网为限制短路电流的影响,一般以辐射状网架运行。本文通过Dist-Flow方法构建交流配电网支路潮流模型为
| \left\{\begin{array}{l} \sum\limits_{v \in \gamma(n)} P_{n v}(t)=P_{m n}(t)-R_{m n}\left|I_{m n}(t)\right|^2-P_n(t) \\ \sum\limits_{v \in \delta(n)} Q_{n v}(t)=Q_{m n}(t)-X_{m n}\left|I_{m n}(t)\right|^2-Q_n(t) \\ P_n(t)=P_{{\text {load }}}^n(t)+P_{{\mathrm{CSSIS}}}^n(t)-P_{{\mathrm{DG}}}^n(t) \\ Q_n(t)=Q_{{\text {load }}}^n(t)-Q_{{\mathrm{DG}}}^n(t) \\ \left|U_n(t)\right|^2=\left|U_m(t)\right|^2-2\left[P_{m n}(t) R_{m n}+\right. \\ \left.\quad Q_{m n}(t) X_{m n}\right]+\left(R_{m n}^2+X_{m n}^2\right)\left|I_{m n}(t)\right|^2 \\ \left|I_{m n}(t)\right|^2=\frac{\left[P_{m n}^2(t)+Q_{m n}^2(t)\right]}{\left|U_m(t)\right|^2} \end{array}\right. | (42) |
式中:v——节点;
γ(n)——在交流配电网中,将n节点作为始端的支路末端节点合集;
Pnv(t),Qnv(t)——第t时段支路n-v的有功、无功功率;
Imn(t)——第t时段支路m-n电流;
Pn(t),Qn(t)——第t时段节点n注入的有功、无功功率;
Ploadn(t),PCSSISn(t),PDGn(t)——第t时段节点n有功负荷、CSSIS有功需求和RES有功输出功率;
Qloadn(t),QDGn(t)——第t时段节点n无功负荷和RES无功输出功率;
Un(t),Um(t)——节点n和m电压;
Xmn——支路m-n电抗。
3.3.2 直流配电网支路潮流约束
根据Dist-Flow方法构建直流配电网支路潮流模型为
| \left\{ {\begin{array}{*{20}{l}} {\sum\limits_{v \in \kappa \left( n \right)} {{P_{{\rm{DC}},nv}}\left( t \right) = {P_{{\rm{DC}},mn}}\left( t \right) - {R_{{\rm{DC}},mn}}{{\left| {{I_{mn}}\left( t \right)} \right|}^2} - {P_{{\rm{DC}},n}}\left( t \right)} }\\ {{P_{{\rm{DC}},n}}\left( t \right) = P_{{\rm{DC}},{\rm{load}}}^n\left( t \right) + P_{{\rm{DC}},{\rm{CSSIS}}}^n\left( t \right) - P_{{\rm{DC}},{\rm{DG}}}^n\left( t \right)}\\ {{{\left| {{U_{{\rm{DC}},n}}\left( t \right)} \right|}^2} = {{\left| {{U_{{\rm{DC}},m}}\left( t \right)} \right|}^2} - 2{P_{{\rm{DC}},mn}}\left( t \right){R_{{\rm{DC}},mn}} + R_{{\rm{DC}},mn}^2{{\left| {{I_{{\rm{DC}},mn}}\left( t \right)} \right|}^2}}\\ {{{\left| {{I_{{\rm{DC}},mn}}\left( t \right)} \right|}^2} = \frac{{P_{{\rm{DC}},mn}^2\left( t \right)}}{{{{\left| {{U_{{\rm{DC}},m}}\left( t \right)} \right|}^2}}}} \end{array}} \right. | (43) |
式中:κ(n)——在直流配电网中,将n节点作为始端的支路末端节点合集;
PDC,nv(t),PDC,mn(t)——第t时段直流支路n-v和m-n有功功率;
RDC,mn——直流支路m-n电阻;
Imn(t)——第t时段支路m-n电流;
PDC,n(t)——第t时段直流节点n注入的有功功率;
PDC,loadn(t)——第t时段直流节点n负荷有功需求;
PDC,CSSISn(t),PDC,DGn(t)——第t时段直流节点n的CSSIS有功需求和RES输出功率;
UDC,n(t),UDC,m(t)——第t时段直流节点n和m电压;
IDC,mn(t)——第t时段直流支路m-n电流。
3.3.3 VSC换流站运行约束
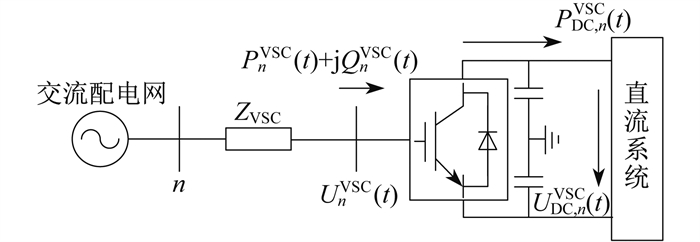
VSC换流站等值电路如图 2所示。其中,VSC换流站内部损耗可以由等值阻抗ZVSC表征。UnVSC(t)和UDC, nVSC(t)分别为第t时段节点n VSC换流站输入的基准相电压与输出直流电压幅值。PnVSC(t)和QnVSC(t)分别为第t时段节点nVSC换流站输入的有功、无功功率。
PnVSC(t)与VSC换流站直流系统注入有功功率PDC, nVSC(t)相等,即:
| P_n^{{\mathrm{VSC}}}(t)=P_{{\mathrm{DC}}, n}^{{\mathrm{VSC}}}(t) | (44) |
另外,VSC换流站正常运行还需要满足下列条件:
| U_n^{{\mathrm{vsc}}}(t)=\frac{\sqrt{3}}{3} \mu M_n(t) U_{{\mathrm{DC}}, n}^{{\mathrm{VSC}}}(t) | (45) |
式中:μ——直流电压利用度;
Mn(t)——第t时段节点nVSC换流站调制度。
3.3.4 配电网安全运行约束
配电网安全运行约束条件为
| \left\{\begin{array}{l} -P_{{\text {pur }}}^{\max } \leqslant P_{{\text {pur }}}(t)-P_{{\text {pur }}}(t-1) \leqslant P_{{\mathrm{pur}}}^{\max } \\ U_j^{\min } \leqslant U_j(t) \leqslant U_j^{\max } \\ -Q_{n, \max }^{{\mathrm{VSC}}} \leqslant Q_n^{{\mathrm{VSC}}}(t) \leqslant Q_{n, \max }^{{\mathrm{VSC}}} \\ P_{m n}^2(t)+Q_{m n}^2(t) \leqslant \bar{S}_{m n}^2 \end{array}\right. | (46) |
式中:Ppurmax——交互功率限值;
Ujmax,Ujmin——节点j电压上下限;
Uj(t)——第t时段节点j电压;
Qn,maxVSC——VSC换流站节点n无功功率调节上限;
Smn——支路m-n视在功率限值。
4 模型求解
本文提出的日前优化调度模型决策变量为
| \begin{aligned} & {\boldsymbol{G}}_1= \\ & {\left[P_{{\mathrm{WT}}}(t), P_{{\mathrm{PV}}}(t), P_{{\mathrm{MT}}}(t), P_{{\mathrm{ESS}}}(t), \omega_{i, {\mathrm{BSS}}}^{{\mathrm{swap}}}(t)\right]} \end{aligned} | (47) |
多时间尺度优化调度模型决策变量为
| \begin{aligned} & {\boldsymbol{G}}_2= \\ & {\left[P_{{\mathrm{WT}}}(t), P_{{\mathrm{PV}}}(t), P_{{\mathrm{MT}}}(t), P_{{\mathrm{ESS}}}(t)\right]} \end{aligned} | (48) |
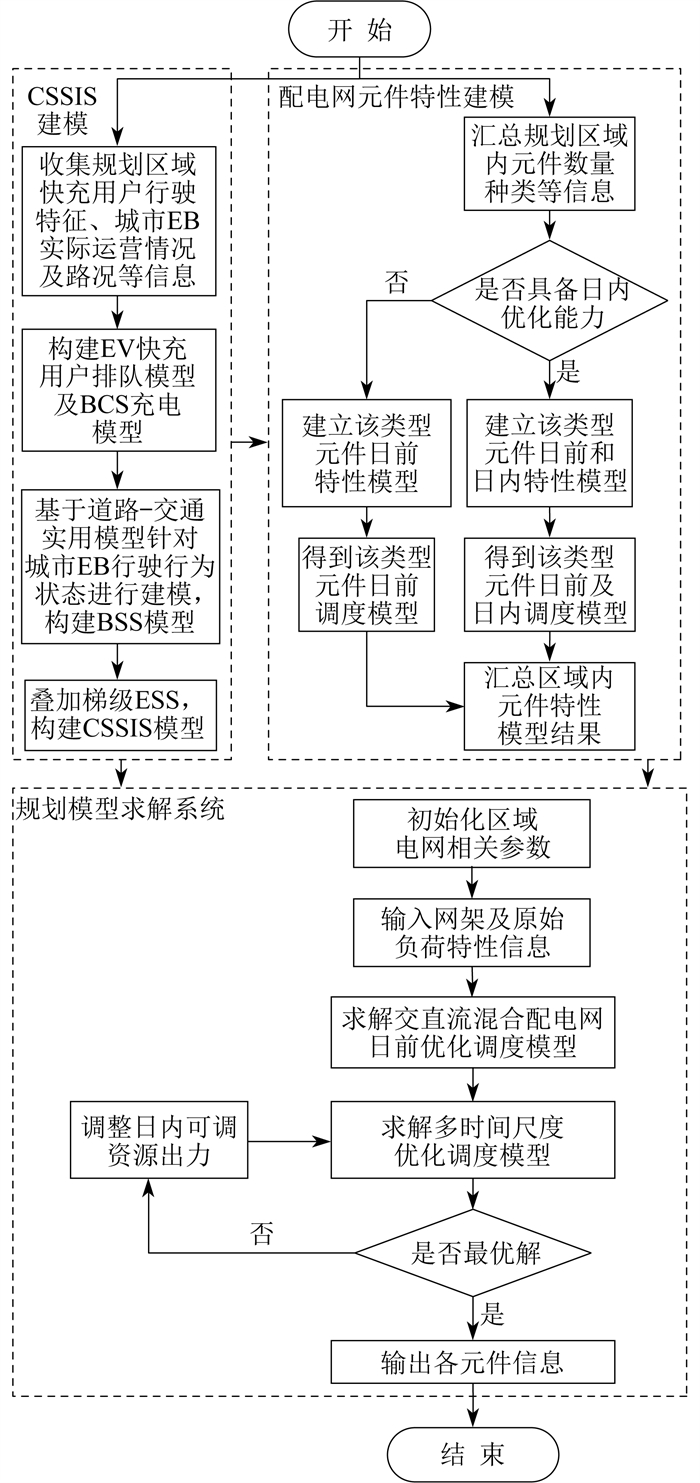
模型的求解流程如图 3所示。
本文构建的优化模型是非凸非线性大规模混合整数组合优化问题[23],属于典型的NP-hard问题,不便直接求解。通过凸松弛法将潮流约束转变为二阶锥规划问题,可用商业软件CPLEX处理二阶锥优化模型。
5 算例分析
5.1 参数设置
本文采用改进IEEE 33节点系统形成50节点测试系统,并结合某区域公共交通运营实际状况为例,进行算例分析。算例在主频为2.1 GHz的Intel i7 CPU和运行内存为32 GB的个人计算机上,通过YALMIP工具箱在MATLAB编译环境下调用ILOG CPLEX 12.8仿真实现。BSS为多条公交线路提供充换电服务。BCS配置10套充电桩,采用直流快充;BSS配置124组备用电池、3台换电机和62套充电桩。
CSSIS提供服务区域内ET数量为160辆。ESS容量为3 MWh,初始荷电状态(State of Charge,SOC)取0.6。VSC1~VSC4的4个VSC换流站参数相同,每个容量为2 MVA,ZVSC=0.5+j1.5 Ω。改进的IEEE 50节点系统如图 4所示。
5.2 优化结果分析
5.2.1 日前优化结果分析
本文提出的日前优化调度模型求解得到的日总综合成本及其组成明细如表 1所示。
表 1
日总综合成本及其组成明细
| 参数 | 数值 |
| 日总综合成本 | 125 541 |
| 基本负荷日购电成本 | 94 154 |
| MT日运行成本 | 6 933 |
| ESS日调度成本 | 1 142 |
| 配电网日损耗成本 | 16 306 |
| 日碳排放成本 | 7006 |
由表 1可以看出,系统日损耗成本与日总综合成本相比较少,是由于WT、PV、CSSIS接入直流配电网,极大地降低了系统损耗。这表明直流配电形式对于RES和EV充换电设施具有更强的适应性和运行经济性。基本负荷日购电成本和日碳排放成本在日总综合成本中占比较大,是由于RES在电网中渗透率相对较低,其输出功率只能部分取代配电网与主网间的交互功率。
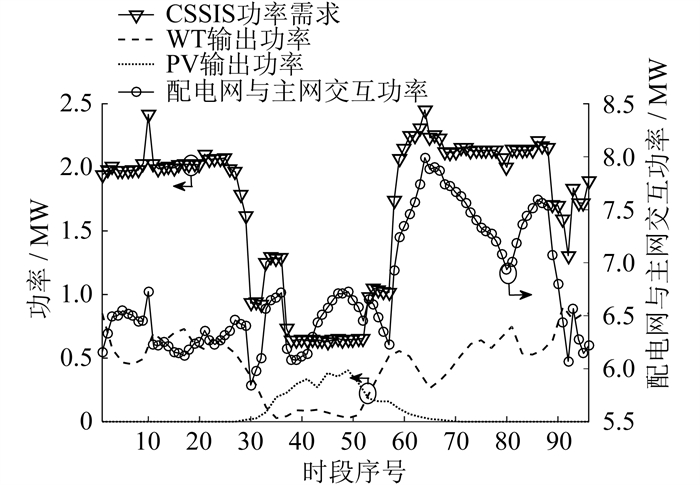
交直流配电网中各元件输出功率优化结果如图 5所示。带圈的箭头表示曲线对应的坐标方向。
由图 5可以看出:DG输出功率在系统中占比相对较低,在未来有进一步提升空间;CSSIS经过电网有序调度,抬升电网谷荷效果较明显。
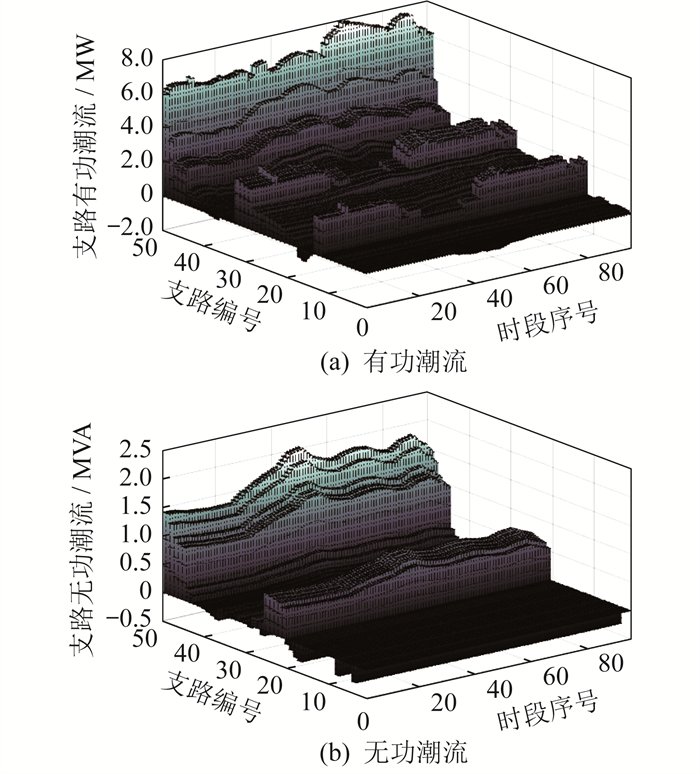
交直流配电网支路有功潮流和无功潮流如图 6所示。
由图 6可以看出:支路34-35和支路47-50在多数时段出现反向有功潮流;出现反向无功潮流的支路数较多,而且主要集中在直流配电网接入交流配电网的节点附近,这是因为VSC换流站可以降低交流配电网的无功功率需求。
各VSC换流站输出功率对比结果如图 7所示。
由图 7可以看出,交直流混合配电网中的VSC换流站可以作为无功电源,有效使用其无功功率的调节能力。
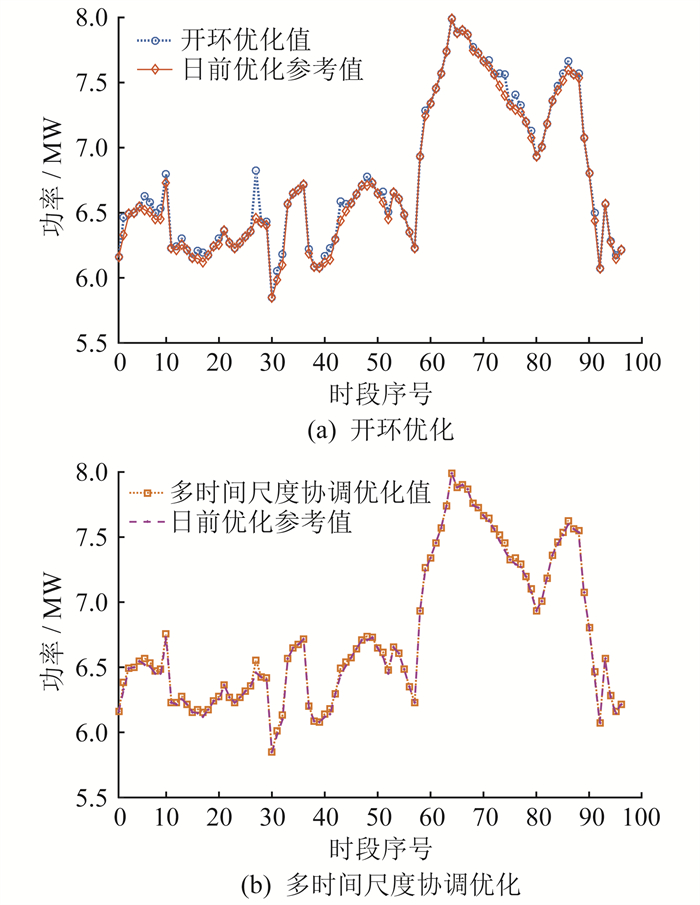
5.2.2 多时间尺度协调优化结果分析
6 结论
(1)新型直流配电形式对于RES和EV充电负荷的集中接入具有更强的适应性和运行经济性,系统损耗更低。交直流混合配电网中的VSC换流站可以作为无功电源,有效使用其无功功率的调节能力,减少交流配电网的无功功率需求。
(2)通过引入多时间尺度协调优化机制,可以有效降低配电网与上级主网交互功率和日前优化参考值之间的偏差,改善因RES输出功率和负荷预测误差导致的不确定性对优化结果的影响。
(3)CSSIS作为一种新兴EV集中充换电服务模式,可以平滑EV充电设施的功率需求曲线,有效缓解电网峰谷差,具备高效参与电网优化运行的潜力。
参考文献
-
[1]马鑫, 郭瑞鹏, 王蕾, 等. 基于二阶锥规划的交直流主动配电网日前调度模型[J]. 电力系统自动化, 2018, 42(22): 144-153.
-
[2]陈鹏浩, 李慧璇, 李锰, 等. 基于改进人工蜂群算法的直流配电网典型应用场景拓扑结构研究[J]. 电力系统保护与控制, 2021, 49(3): 57-65.
-
[3]张释中, 裴玮, 杨艳红, 等. 交直流混合配电网结构优选和设备容量优化[J]. 中国电机工程学报, 2020, 40(9): 2766-2777.
-
[4]周敏, 吕振宇, 王琦, 等. 直流配电网换流站分布式有功-电压二级优化控制策略[J]. 中国电机工程学报, 2020, 40(24): 8002-8011.
-
[5]刘飞, 熊晓琪, 查鹏程, 等. 直流配电网网架结构与分布式光伏多目标协同优化[J]. 中国电机工程学报, 2020, 40(12): 3754-3765.
-
[6]王守相, 陈思佳, 谢颂果. 储能与换流站协调经济调度[J]. 电力系统自动化, 2017, 41(11): 85-91.
-
[7]ZENGINIS I, VARDAKAS J, ZORBA N, et al. Performance evaluation of a multi-standard fast charging station for electric vehicles[J]. IEEE Transaction Smart Grid, 2018, 9(5): 4480-4489. DOI:10.1109/TSG.2017.2660584
-
[8]FAN P Y, SAINBAYAR B, REN S L. Operation analysis of fast charging stations with energy demand control of electric vehicles[J]. IEEE Transactions on Smart Grid, 2015, 6(4): 1819-1826. DOI:10.1109/TSG.2015.2397439
-
[9]刘方, 杨秀, 时珊珊, 等. 考虑不确定因素下含充换储一体化电站的微网能量优化[J]. 电网技术, 2015, 39(3): 669-676.
-
[10]何晨可, 韦钢, 朱兰, 等. 电动汽车充换放储一体化电站选址定容[J]. 中国电机工程学报, 2019, 39(2): 479-489.
-
[11]冯俊淇, 解大, 贾玉健, 等. 电动汽车充放储一体化电站调度参数分析[J]. 电网技术, 2013, 37(12): 3325-3330.
-
[12]楚皓翔, 解大, 娄宇成, 等. 电动汽车智能充放储一体化电站无功电压调控策略[J]. 电力自动化设备, 2014, 34(11): 48-54.
-
[13]YUAN H T, WEI G, ZHU L, et al. Optimal scheduling for micro-grid considering EV charging-swapping-storage integrated station[J]. IET Generation, Transmission & Distribution, 2020, 14(6): 1127-1137.
-
[14]袁洪涛, 韦钢, 张贺, 等. 计及充换储一体站的主动配电网鲁棒优化调度[J]. 中国电机工程学报, 2020, 40(8): 2453-2468.
-
[15]邵尹池, 穆云飞, 余晓丹, 等. "车-路-网"模式下电动汽车充电负荷时空预测及其对配电网潮流的影响[J]. 中国电机工程学报, 2017, 37(18): 5207-5219.
-
[16]张曦予, 李秋硕, 陶顺, 等. 电动公交车充电站功率需求影响因素分析及建模[J]. 现代电力, 2014, 31(1): 28-33.
-
[17]裴蕾, 卫志农, 陈胜, 等. 交直流混合配电网多阶段随机优化调度模型[J]. 电力系统保护与控制, 2022, 50(14): 23-32.
-
[18]肖文乔, 刘继春. 计及需求响应和分布鲁棒博弈的交直流配电网低碳运行管控[J/OL]. 电测与仪表: 1-12(2022-06-06)[2023-05-30]. http://kns.cnki.net/kcms/detail/23.1202.TH.20220602.1615.002.html.
-
[19]高崇, 王天霖, 张俊潇, 等. 基于协同进化NSGA-Ⅱ的多目标交直流配电网规划方法[J]. 电测与仪表, 2023, 60(8): 133-137.
-
[20]董雷, 陈卉, 蒲天骄, 等. 基于模型预测控制的主动配电网多时间尺度动态优化调度[J]. 中国电机工程学报, 2016, 36(17): 4609-4617.
-
[21]李嘉龙, 陈雨果, 刘思捷, 等. 考虑碳排放成本的电力市场均衡分析[J]. 电网技术, 2016, 40(5): 1558-1563.
-
[22]赵晶晶, 朱炯达, 刘帅, 等. 基于集群划分的配电网多时间尺度分布式有功-无功协同优化方法[J/OL]. 电测与仪表: 1-10(2022-06-13)[2023-05-30]. http://kns.cnki.net/kcms/detail/23.1202.TH.20220610.1827.008.html.
-
[23]彭月, 熊炜, 袁旭峰, 等. 基于混合整数二阶锥规划的主动配电网最优潮流研究[J]. 电测与仪表, 2023, 60(5): 139-144.