|
|
|
发布时间: 2024-04-28 |
智能设备与测量 |
|
|
|
收稿日期: 2023-06-12
基金项目: 国家自然科学基金(51607111)
中图法分类号: TM614
文献标识码: A
文章编号: 2096-8299(2024)02-0129-06
|
摘要
双馈风机通过附加虚拟惯性控制和下垂控制参与电力系统调频,但固定的控制系数无法发挥风机实际调频潜力。针对这一问题,提出了一种将遗传算法和模糊控制(GA-FC)相结合的变系数风机调频优化控制策略。首先,为提高调频时功率支撑能力,分析了超速减载控制,对不同风速下减载率进行拟合;然后,参考其他文献虚拟惯性控制系数整定结果,对下垂控制系数进行整定,再通过GA-FC实现动态调整控制系数,实时挖掘风机实际调频能力;最后,在MATLAB/Simulink搭建仿真模型,对所提策略进行验证。结果表明所提策略能够有效提升系统频率支撑。
关键词
双馈风机; 下垂控制; 超速减载; 模糊控制; 遗传算法
Abstract
Doubly fed induction generator participates in power system frequency regulation by attaching virtual inertia and sag control, but the fixed control coefficients cannot realize the actual frequency regulation potential of the wind turbine.To address this problem, a genetic algorithm and fuzzy control (GA-FC) based optimal control strategy for variable coefficient wind turbine frequency regulation is proposed. First, in order to improve the power support capability at frequency regulation, the overspeed load shedding control is analyzed and the load shedding rate at different wind speeds is fitted; then by referring to other literature on the results of virtual inertia control coefficient rectification, the sag control coefficient is rectified and the control coefficient is dynamically adjusted by GA-FC to explore the actual frequency regulation capability of the wind turbine in real time; finally, a simulation model is built in MATLAB/Simulink to verify the proposed strategy, and the results show that the proposed strategy can effectively improve the system frequency support.
Key words
doubly fed induction generator; droop control; over⁃speed load shedding; fuzzy control; genetic algorithm
双馈风机具有成熟可靠、成本低、易维护等优点,但在电力系统频率变化时无法主动响应[1]。当大规模风力发电并网后,会导致系统的惯性降低以及调频能力减弱,对系统的稳定性和安全运行产生不良影响[2]。因此,风电机组应主动承担调频任务。对于双馈风机参与调频目前已有大量研究,主要控制方法有虚拟惯性控制[3]、下垂控制[4]和减载控制[5]。
虚拟惯性控制和下垂控制两者结合称之为综合惯性控制。虚拟惯性控制对频率变化率起到短时支撑的作用,下垂控制则有效改善系统频率偏差[6]。文献[7]利用综合惯性控制使风机转速与系统频率耦合,但当风速发生变化时,该策略的鲁棒性较差。目前,针对双馈风机调频控制的研究热点之一是控制系数优化,常规综合惯性控制采用给定固定的控制系数,文献[8]给出了虚拟惯性控制系数和下垂控制系数对系统频率变化的影响趋势,随着控制系数增大,风电逐渐深度参与调频,但忽略了风机调频能力有限,过大的控制系数将导致风机失去调频能力。有学者提出对控制系数整定后进行变系数控制。文献[9]将风速分区,针对低、中、高风速采取不同的整定策略,进行变下垂控制调频。文献[10]给出了比例-微分(Proportional-Derivative,PD)虚拟惯性控制方式相关参数的整定公式,提出了一种改进的虚拟惯性控制调频方法,可实时调整控制系数。文献[11]提出通过模糊控制(Fuzzy Control,FC)调整控制系数,实现变系数控制,但模糊控制规则完全依据经验设置,具有一定局限性。上述控制都是在最大功率点跟踪(Maximum Power Point Tracking,MPPT)控制下仅通过综合惯性控制进行调频,此时风机提供的功率支撑将十分有限,一般会结合减载控制进行调频。
减载控制分为变桨减载控制和超速减载控制。这两种控制都是通过提前预留减载功率,在风电并网需要调频时进行释放,使风机充分参与系统调频[12]。变桨减载控制响应速度较慢且风轮容易产生机械损耗,一般不予考虑。超速减载控制通过风机释放减载储备的转子动能,在附加调频控制器的作用下,实现转子动能与有功出力之间的转换,进而实现系统频率调整[13]。文献[14]将转子惯性控制与超速减载控制相结合,实现了协调控制,得出与风速耦合的变系数调频控制。文献[15]分别在额定风速以上和以下对虚拟惯性系数进行整定,并通过变风速验证了控制策略的有效性。需要指出的是,上述减载控制均是通过设定固定减载系数实现,具有一定局限性。由于风速的不稳定性,不同风速下减载相同的功率需要设定不同的减载系数,否则当减载功率与风速不匹配时,容易导致风机失去调频能力。
针对以上问题,本文在研究双馈风机参与电网调频控制方法的基础上,提出了一种将遗传算法和模糊控制(Genetic Algorithm and Fuzzy Control,GA-FC)相结合的变系数风机调频优化控制策略。首先,将超速减载控制与综合惯性控制相结合,实现了协调控制,并拟合了仅通过超速减载控制进行减载的备用容量和风速的关系;然后,参考文献[16]的虚拟惯性控制系数整定结果,提出了一种考虑微电网调频的下垂控制整定方法,在此基础上提出GA-FC调频优化控制策略,实现动态调整调频参数;最后,基于MATLAB/ Simulink搭建算例调频模型,验证所提控制策略的有效性。
1 双馈风机调频策略研究
1.1 超速减载控制参与调频
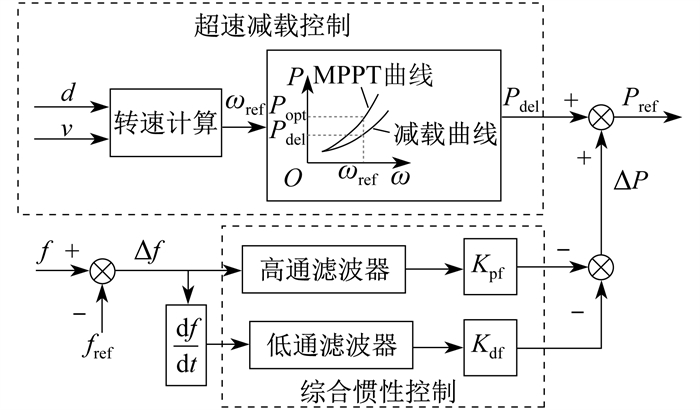
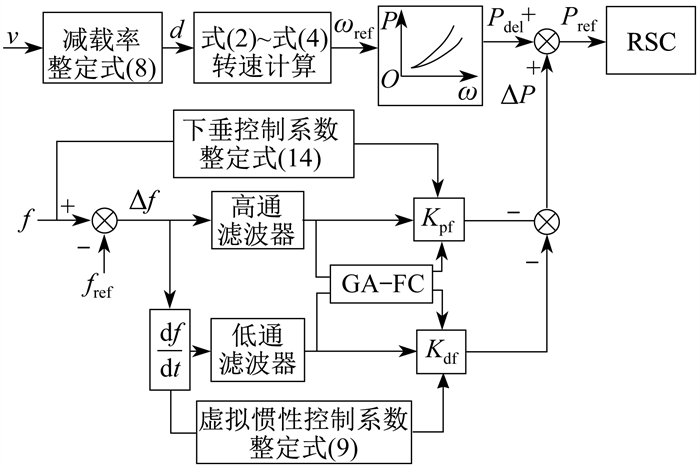
双馈风机转子转速和频率的解耦,使双馈风机无法参与系统调频。通过在双馈风机内部引入综合惯性控制,可以模拟传统同步机的惯性特性和调速器的下垂特性,从而释放隐藏在转子内部的动能,参与系统调频。超速减载控制是通过控制风机转子转速的快慢,使风机的有功功率偏离MPPT曲线运行于减载曲线上,留出一部分有功功率备用参与调频,在综合惯性控制的基础上增加超速减载控制来提高风机频率支撑能力。超速减载控制参与调频控制策略如图 1所示。
其中,d为超速减载控制的减载率,v为风速,ωref为风机参考转子转速,P为风机有功功率,ω为风机转子转速,Popt为风机在某风速下运行的最大功率追踪值,Pdel为减载输出功率,Pref为双馈风机参考输出功率,f和fref分别为系统频率和参考值,Δf为频率偏差,df/dt为频率变化率,Kpf和Kdf分别为下垂控制系数和虚拟惯性控制系数,ΔP为双馈风机由频率变化产生的额外输出功率。模拟同步机发生频率响应,双馈风机由频率变化产生的额外输出功率ΔP为
| $ \Delta P=-K_{{\mathrm{pf}}} \Delta f-K_{{\mathrm{df}}} \frac{{\mathrm{d}} f}{{\mathrm{~d}} t} $ | (1) |
假定某风速下,风机减载d等价于风能利用系数Cp降低d。Cp由叶尖速比λ与桨距角β决定,其数学关系如下:
| $ \lambda=\frac{\omega_{{\mathrm{ref}}} r}{v} $ | (2) |
| $ \frac{1}{\lambda_{{\mathrm{i}}}}=\frac{1}{\lambda+0.08 \beta}-\frac{0.0035}{\beta^3+1} $ | (3) |
| $ C_{{\mathrm{p}}}=0.22\left(\frac{116}{\lambda_{{\mathrm{i}}}}-0.4 \beta-5\right) {\mathrm{e}}^{\frac{-12.5}{\lambda_{{\mathrm{i}}}}} $ | (4) |
式中:λi——中间量;
r——风轮半径。
风机最大功率追踪值Popt和减载输出功率Pdel分别为
| $ P_{{\mathrm{opt}}}=\frac{\rho}{2} \pi r^2 C_{{\mathrm{p}}}\left(\frac{r}{\lambda}\right)^3 \omega_{{\mathrm{ref}}}^3 $ | (5) |
| $ P_{{\mathrm{del}}}=(1-d) P_{{\mathrm{opt}}} $ | (6) |
式中:ρ——空气密度。
超速减载控制具体实现过程如下:由于β在MPPT区保持为零,通过查找风能利用系数Cp的数据,可获知减载状态下Cp以及与之相对应的λ,由式(2)可求出参考转子转速ωref,再根据式(5)、式(6)可得到减载输出功率Pdel。
由图 1可知,双馈风机参考输出功率Pref由综合惯性控制输出功率ΔP与超速减载控制输出功率Pdel共同决定。
| $ P_{{\text {ref }}}=\varDelta P+P_{{\text {del }}} $ | (7) |
1.2 超速减载率分析
双馈风机在超速减载状态下运行时,不同风速下风电机组的减载能力变化大。风速较低时,采用较高的减载率,会造成风能利用率降低,浪费风能,同时系统惯性响应能力也会减弱,造成频率偏差过大,影响电力系统稳定性。为得到减载率d与风速v的关系,在保证系统频率稳定的前提下,通过在不同风速下进行仿真,可求取转子转速达到额定转速时双馈风机的减载率。减载率与风速的关系式拟合为
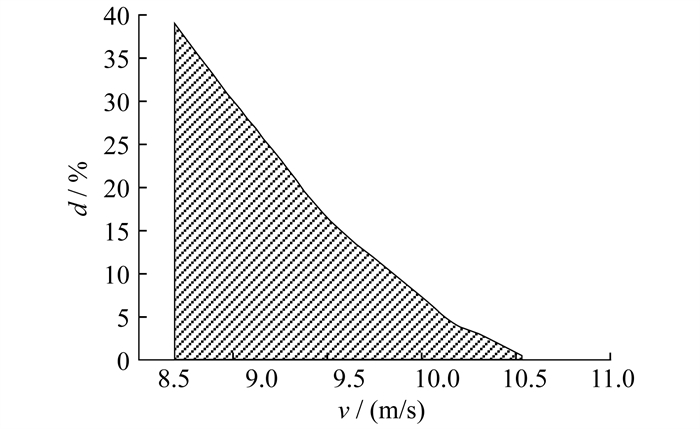
| $ d=5.511 v^2-124.217 v+697.053 $ | (8) |
参考式(8)绘制不同风速下减载率如图 2所示。图 2中阴影部分为可减载范围。
由图 2可知:风速较低时,风机减载能力较强;受额定转速限制,风速越高,超速减载控制的减载率越小,留给风机的减载预留量越小,并且呈加快趋势。这给低中风速下进行调频的超速减载控制提供了一定的参考,避免电机因转速过快而损坏。
2 综合惯性控制系数整定
2.1 虚拟惯性控制系数的整定
常规Kdf的整定通过风机转速改变,求取风机转子动能改变量,模拟同步发电机特性,可得到此过程中风机用于调频的有功功率变化量。本文直接引用文献[16]虚拟惯性控制系数Kdf的整定结果。
| $ K_{{\mathrm{df}}}=\frac{2 H P_{{\mathrm{N}}} f}{f_{{\mathrm{N}}}^2} $ | (9) |
式中:H——风机惯性时间常数;
PN——风机额定容量;
fN——风机额定频率。
由式(9)可知,虚拟惯性控制系数Kdf由系统频率f决定,当f取不同值时,可通过拟合得到整定后的系数Kdf。
2.2 下垂控制系数的整定
本文从电网调频角度考虑,同步发电机的下垂特性为
| $ \Delta P_{{\mathrm{m}}}=-\frac{1}{R} \Delta \omega_{{\mathrm{s}}} $ | (10) |
式中:ΔPm——同步发电机功率增量;
R——调差系数;
Δωs——同步发电机转子转速变化量。
双馈风机参与电力系统调频的转子运动方程为
| $ \Delta P_{{\mathrm{m}}}+\Delta P_{{\text {wind }}}-\Delta P_1=2 H_{{\mathrm{s}}} \frac{{\mathrm{d}} \Delta \omega_{{\mathrm{s}}}}{{\mathrm{d}} t}+D \Delta \omega_{{\mathrm{s}}} $ | (11) |
式中:ΔPwind——风电调频输出功率;
ΔPl——扰动负荷;
Hs——电力系统惯量,本文选取频率初始变化时刻瞬时值;
D——阻尼系数,取1。
其中,
| $ H_{{\mathrm{s}}}=\left|\frac{\Delta P_1}{{\mathrm{~d}} \Delta f /\left.{\mathrm{d}} t\right|_{t=0^{+}}}\right| $ | (12) |
风机下垂控制输出功率ΔPwind1为
| $ \Delta P_{{\text {wind1 }}}=K_{{\mathrm{pf}}} \Delta f $ | (13) |
上述均取标幺,联立式(10)至式(13)可得:
| $ K_{{\mathrm{pf}}}=\frac{1}{\Delta f}\left(2 H_{{\mathrm{s}}} \frac{{\mathrm{d}} \Delta f}{{\mathrm{~d}} t}+\Delta P_1\right)+\frac{1+R}{R} $ | (14) |
由式(14)可知,下垂控制系数Kpf由频率偏差Δf与频差变化率dΔf/dt决定,通过仿真可求取Δf变化时Kpf的不同整定值。
3 基于GA-FC的优化算法设计
3.1 模糊控制设计
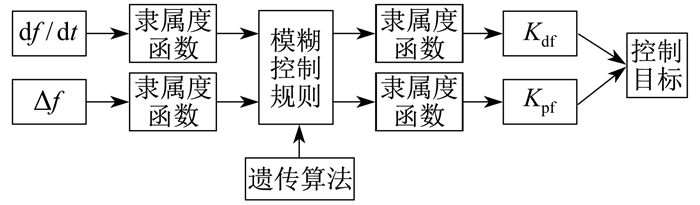
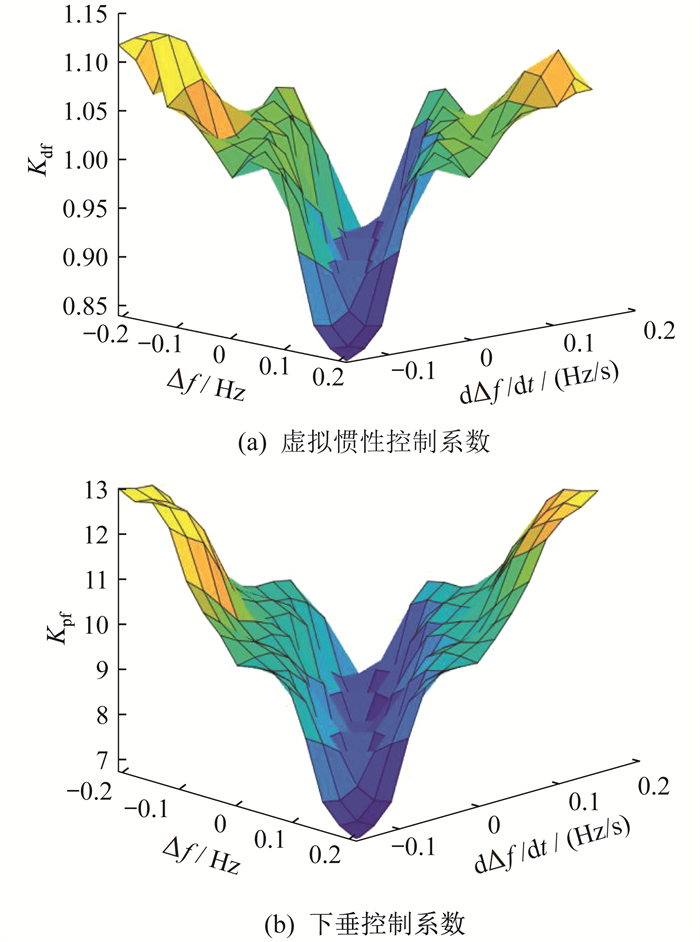
模糊控制应用广泛,具有不需要精确数学模型、鲁棒性强等优点。模糊控制器设置依据为:频率波动初始阶段,需要尽快释放转子动能,此时增大虚拟惯性控制系数和下垂控制系数,分别抑制频率变化率和改善频率最低点,当频率达到最低点时,控制系数也达到最大;频率即将上升到稳态值的阶段,为防止频率二次跌落,应同时减小虚拟惯性控制系数和下垂控制系数,加快转速恢复,这个过程中风机输出功率逐渐恢复到MPPT,频率也逐渐恢复。本文以频率偏差Δf和频差变化率dΔf/dt作为模糊控制器的输入变量,论域范围分别选取-0.2~0.2 Hz和-0.15~0.15 Hz/s;以虚拟惯性控制系数Kdf和下垂控制系数Kpf作为模糊控制器的输出变量,参考式(9)和式(14)进行动态调整,论域范围分别为0.8~1.2和6~13。以上两个输入和两个输出变量的模糊子集均选为7个,且QS、MS、S、M、L、ML、NL分别表示负大、负中、负小、零、正小、正中、正大。选取高斯曲线作为隶属度函数,去模糊法为重心法。
3.2 遗传算法优化设计
3.3 基于GA-FC的机组调频策略
双馈风机参与系统调频的GA-FC调频优化策略如图 5所示。Kdf和Kpf可根据频率扰动变化实时调整,通过计算双馈风机由频率变化产生的额外输出功率ΔP,并与超速减载控制后的减载输出功率Pdel叠加,得到双馈风机参考输出功率Pref,将其输入到机组转子侧变流器(Rotor Side Convertor,RSC)调整有功输出功率参与调频。
4 仿真验证
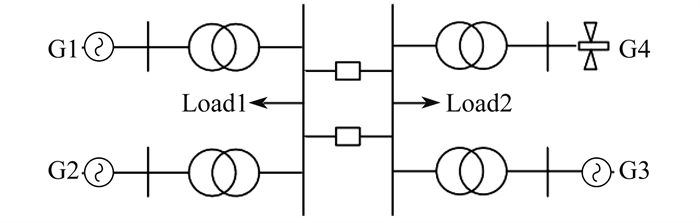
使用MATLAB/Simulink仿真平台搭建的4机2区算例调频系统如图 6所示。其包含3台同步发电机组G1、G2、G3,等效风电场G4,两个负荷Load1和Load2。
等效风电场由125台双馈风机组成,每台单机容量为1.5 MW,风电渗透率为10%,超速减载率为7%,采用负荷突增和负荷突减实验,验证本文所提策略的有效性。仿真场景如表 1所示。表 1中,“√”和“Δ分别表示对应模块是否参与调频,场景1下风电不参与调频,场景2在超速减载控制下加入综合惯性控制,其中采用的Kdf和Kpf分别为1和8,场景3增加了模糊控制策略,场景4为本文所提策略。
表 1
仿真场景
| 场景 | 综合惯性控制 | 超速减载 | 模糊控制 | 遗传算法 |
| 1 | × | × | × | × |
| 2 | √ | √ | × | × |
| 3 | √ | √ | √ | × |
| 4 | √ | √ | √ | √ |
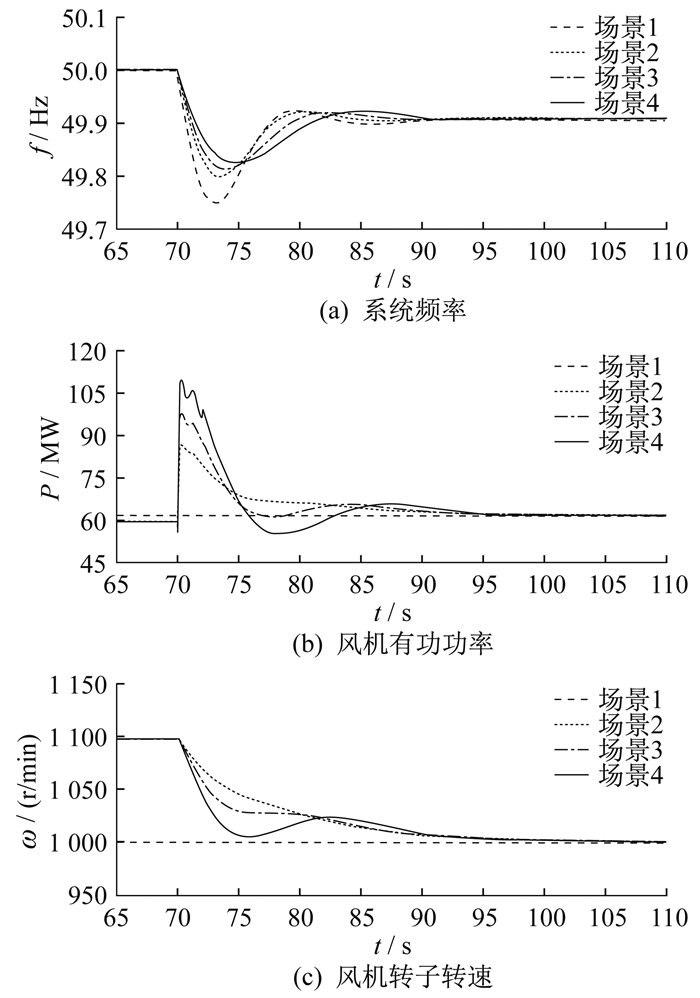
在风速为10 m/s情况下进行仿真,模拟发生负荷突增情景。Load1为1 400 MW稳态负荷,Load2在第70 s增加100 MW扰动负荷。频率向下扰动的仿真结果如图 7所示。
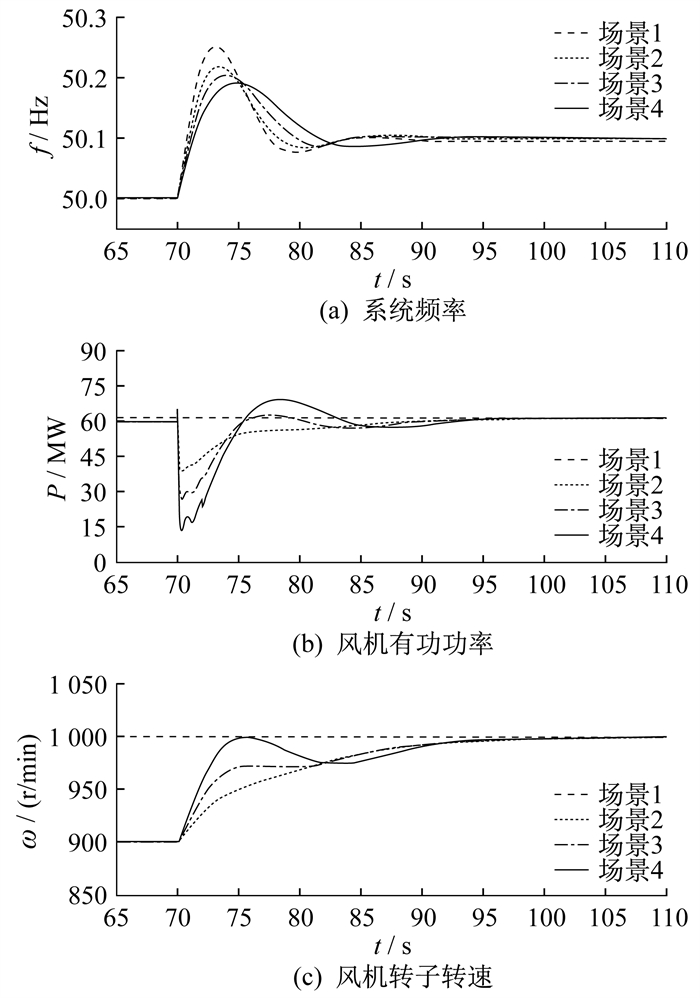
同样在风速为10 m/s情况下进行仿真,模拟发生负荷突减情景。Load1为1 300 MW稳态负荷,Load2在第70 s减少100 MW扰动负荷。频率向上扰动的仿真结果如图 8所示。
由图 7和图 8可知,相同扰动下,采取不同控制方法,系统频率发生响应的程度不同。调频开始后,风机转子转速响应系统频率变化,不断释放转子动能,频率偏差逐渐减小;当频率变化进入稳态时,双馈风机也回到MPPT控制,风机转子转速停止响应。在风电不参与调频的情况下,频率下降速率和幅值最大,由于风机有功功率、转子转速只根据风速进行调整,因此保持恒定。加入超速减载控制后,双馈风机可释放的转子动能大幅度增加,对比场景2和场景3可知,模糊控制可以根据调频阶段动态改变控制系数,风机调频能力也随之增加。
对比场景3和场景4可知:突增负荷时,本文所提策略有效延缓了频率降到最低点的时间且最低点频率值有所提升,最大频率偏差从0.161 Hz减小到0.158 Hz,风机最大有功功率标幺值由0.377 p.u. 增大到0.452 p.u(. 转子转速和功率均采用标幺值);突减负荷时,最大频率偏差从0.203 Hz减小到0.191 Hz,风机最大有功功率标幺值由0.218 p.u.增大为0.398 p.u.。综上所述,本文所提GA-FC调频优化控制策略可以在调频阶段释放更多的转子动能,最大频率偏差相比之下也最小,有效改善了系统频率的稳定性。
5 结语
本文针对双馈风机调频参与度不深的问题进行了研究,从系统调频角度考虑,提出了一种下垂控制系数整定方法,并根据整定结果初步设计了模糊控制规则;针对模糊控制规则设置依赖于经验的问题,提出了一种基于GA-FC的变系数风机调频优化控制策略。
超速减载控制通过提前预备调频功率可以大幅度增加风机调频能力。固定的控制系数不能发挥风机实际调频能力,将频率与控制系数耦合后,采用GA-FC进行变系数调频控制,可以有效克服双馈风机调频控制有功输出功率不足的问题。
本文只在固定风速下进行了仿真情况,未对随机风速下的情况进行研究。同时,本文只对模糊控制规则进行了优化,并未考虑模糊控制隶属度函数的影响。这些将是今后研究的重点。
参考文献
-
[1]唐西胜, 苗福丰, 齐智平, 等. 风力发电的调频技术研究综述[J]. 中国电机工程学报, 2014, 34(25): 4304-4314.
-
[2]伍双喜, 谭嫣, 刘思宁, 等. 风电机组参与调频的系统频率响应模型[J]. 南方电网技术, 2022, 16(10): 48-56.
-
[3]马静, 李益楠, 邱扬, 等. 双馈风电机组虚拟惯量控制对系统小干扰稳定性的影响[J]. 电力系统自动化, 2016, 40(16): 1-7.
-
[4]姚亚鑫, 刘锋, 刘璋玮, 等. 面向长期调频的风机非线性下垂控制设计[J]. 电网技术, 2018, 42(6): 1845-1852.
-
[5]曹军, 王虹富, 邱家驹. 变速恒频双馈风电机组频率控制策略[J]. 电力系统自动化, 2009, 33(13): 78-82.
-
[6]乔颖, 郭晓茜, 鲁宗相, 等. 考虑系统频率二次跌落的风电机组辅助调频参数确定方法[J]. 电网技术, 2020, 44(3): 807-815.
-
[7]张冠锋, 杨俊友, 孙峰, 等. 基于虚拟惯量和频率下垂控制的双馈风电机组一次调频策略[J]. 电工技术学报, 2017, 32(22): 225-232.
-
[8]李少林, 王伟胜, 张兴, 等. 风力发电对系统频率影响及虚拟惯量综合控制[J]. 电力系统自动化, 2019, 43(15): 64-73. DOI:10.7500/AEPS20190103005
-
[9]潘文霞, 全锐, 王飞. 基于双馈风电机组的变下垂系数控制策略[J]. 电力系统自动化, 2015, 39(11): 126-131. DOI:10.7500/AEPS20140825011
-
[10]陈宇航, 王刚, 侍乔明, 等. 一种新型风电场虚拟惯量协同控制策略[J]. 电力系统自动化, 2015, 39(5): 27-33.
-
[11]LIU Q Y, SI Y D, HUO X L, et al. Coordination control based on virtual inertial time constant and fuzzy logic control for power system with wind farm[C]//Iecon 2020 The 46th Annual Conference of the IEEE Industrial Electronics Society. Singapore: IEEE, 2020: 5157-5162.
-
[12]赵冬梅, 许瑞庆, 郑立鑫, 等. 全风况下双馈风机参与调频的协调控制策略研究[J]. 电力系统保护与控制, 2017, 45(12): 53-59. DOI:10.7667/PSPC160983
-
[13]LI S H, WANG M. A novel model of the lower active power limit (LAPL) of DFIG under overspeed mode[J]. International Journal of Electrical Power & Energy Systems, 2021, 125: 106439.
-
[14]陈斌, 王德林, 张俊武, 等. 双馈风电机组参与电网一次调频的多风速段综合控制及变参数整定[J]. 电工电能新技术, 2018, 37(11): 40-47.
-
[15]李颖颖, 王德林, 范林源, 等. 双馈风电机组限功率运行下频率稳定的变系数控制策略[J]. 电网技术, 2019, 43(8): 2910-2917.
-
[16]黄道火. 发电机组一次调频原理及试验[M]. 北京: 中国电力出版社, 2017: 32-34.