|
|
|
发布时间: 2024-04-28 |
其他研究 |
|
|
|
收稿日期: 2023-11-18
基金项目: 上海市科技支撑碳达峰碳中和专项(21DZ1207400);国家自然科学基金(52376070)
中图法分类号: TK513.1
文献标识码: A
文章编号: 2096-8299(2024)02-0191-06
|
摘要
建筑外墙安装的微型聚光器在高层建筑太阳能利用技术中具有巨大的应用潜力。结合太阳辐射资源和聚光器光学效率,提出了计算加权平均光学效率的数学模型,并基于该模型,研究了双焦点微型聚光器在不同安装方式下的光学性能。对4个城市全年加权平均光学效率的计算结果显示:双焦点微型聚光器安装于建筑外墙时,夏季效率最低,冬季效率最高;安装地纬度对不同安装方式下聚光器的光学性能有较大影响。此外,基于光学模拟结果,分析了安装于聚光器端部的反射膜对余弦损失的抑制作用。
关键词
太阳能利用技术; 微型聚光器; 光学性能
Abstract
Micro⁃concentrators installed on building facades have great potential in the field of solar energy utilization technology for high ⁃ rise buildings. A model is proposed to calculate the weighted average optical efficiency, which integrates two dimensions of solar radiation resources and the optical efficiency.This model is used to investigate the optical performance of a dual⁃focus micro⁃concentrator under different tracking methods.By calculating the annual weighted average optical efficiency of 4 cities, the result reveals that the efficiency is at its lowest in summer and highest in winter when the micro ⁃ concentrator is installed on facades. The latitude of the installation site has a greater effect on the optical efficiency. In addition, this paper analyzes the suppressive effect of the reflective film installed at the end of the concentrator on reducing cosine losses based on the optical simulation results.
Key words
solar energy utilization technology; micro concentrator; optical performance
中国作为能耗大国,建筑能耗约占总能耗的32%。作为传统清洁能源,太阳能在建筑节能领域的应用可有效降低建筑能耗,是助力实现“碳达峰、碳中和”目标的重要手段[1-2]。随着高层建筑在我国城市建筑中的占比逐年递增,研究者开始关注太阳能在高层建筑中的应用。文献[3]估算了10个典型城市的太阳能应用潜力,结果显示,高层建筑外墙的太阳能资源利用远高于屋顶。基于线性菲涅尔原理的太阳能微型聚光器结构紧凑,在保持收集面积不变的同时大幅减少了散热面积,提升了聚光器的集热效率[4]。文献[5-6]分别在夏季与冬季对微型聚光器进行了户外全天集热测试,结果显示:微型聚光器的集热效率比商用平板集热器高11%,在集热性能上具有优势。文献[7]设计了一种连杆偏置轴镜元布局的聚光器,通过模拟发现,相较于传统镜场设计,该聚光器的光学效率提升了10.7%。由于线性菲涅尔聚光器采用单轴跟踪方式,当应用于建筑外墙时,其镜场的布置依据跟踪方式的不同,可分为太阳高度角跟踪与太阳方位角跟踪两种方式。文献[8]通过参考塔式太阳能电站,利用矢量分析计算了线性菲涅尔电站不同跟踪方式的末端损失、大气衰减及余弦系数,针对不同应用,找出了合理的镜场分布方式。文献[9]通过耦合多目标遗传算法与蒙特卡洛法,计算平面上不同跟踪方式下菲涅尔聚光器光学综合性能最优解。然而,上述研究均忽视了太阳辐照度受不同地区季节和天气的变化影响,且应用场景多针对大型电站。本文考虑到建筑太阳能聚光器应用方式的特殊性,结合太阳辐射资源与聚光器光学效率两因素,分析了双焦点微型聚光器安装于建筑外墙时,不同安装方式对其效率的影响。
1 研究方法
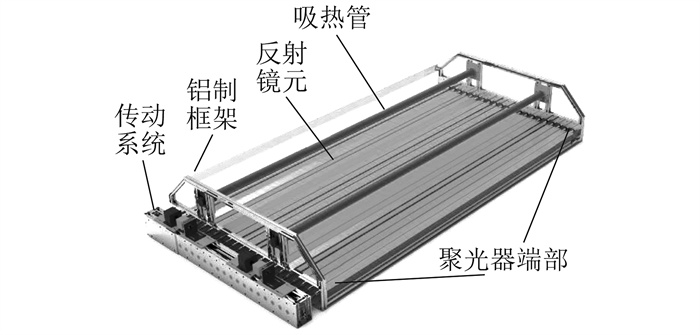
1.1 聚光器设计
1.2 加权平均光学效率简介
目前,大多数研究以逐时光学效率作为表征聚光器性能的光学参数。逐时光学效率为接收器上获得的太阳辐射能与射至镜场上获得的太阳辐射能的比值[10]。因此,逐时光学效率只能定量描述聚光器本身的光学性能。然而,如果仅从聚光器本身考虑,会忽视太阳辐射度变化对聚光器整体性能的影响。对于特定的聚光器,其光学效率除了与其结构密切相关外,也会随着聚光器安装位置、与水平面的安装角度及时间的改变而不断变化。对于建筑整合的太阳能收集器而言,更应关注不同安装方式和建筑的地理位置对太阳能收集效率的影响。为了综合分析聚光器全年不同时间的光学效率,本文提出的聚光器加权平均光学效率
| $ \bar{\eta}=\frac{\sum\limits_{t=T_{\text{s}}}^{T_{\text{o}}}\left(\eta_t E_t\right)}{\sum\limits_{t=T_{\text{s}}}^{T_{\text{o}}}\left(E_t\right)} $ | (1) |
式中:ηt——聚光器逐时光学效率;
Et——聚光器安装地的逐时平均直射辐照度,W/m2;
Ts,To——聚光器工作的开始和结束时间,均为当地平太阳时。
由式(1)可知,为了计算聚光器的加权平均光学效率,需要分别获得聚光器本身的逐时光学效率和逐时辐照度。其计算过程如下。
步骤1 依据重点关注的聚光器安装建筑物的地理位置,获得当地的经纬度、太阳高度角及方位角的变化范围和全年辐照度的变化数据[11-12]。
步骤2 利用光学仿真软件,逐一对不同地区、季节、时刻的聚光器光学性能进行仿真计算。在仿真过程中提取太阳方位角、高度角及聚光器效率。
步骤3 通过数据拟合,获得不同地区聚光器光学性能与太阳方位角之间的函数关系。
步骤4 利用聚光器光学性能与太阳方位角的函数关系及太阳能聚光器安装地的逐时辐照度数据,计算聚光器在不同日期下的全天加权平均光学效率。
1.3 聚光器逐时光学效率
建立光学仿真模型对各太阳入射角度下的聚光器光学性能进行模拟,并通过数据拟合的方法构建聚光器光学效率与太阳高度角和方位角之间的函数关系。
1.3.1 聚光器光学模型
本文采用基于蒙特卡洛的射线跟踪法建立仿真模型,并对不同太阳入射角度下的聚光器光学性能进行计算。
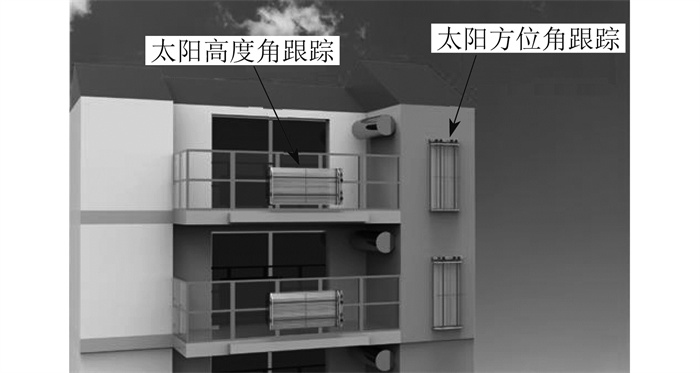
根据上述聚光器的设计参数,建立光学模型。为减少末端损失,可在聚光器两端部内侧安装反射膜。当聚光器跟踪太阳高度角时,将反射膜安装于两端部;当聚光器跟踪太阳方位角时,仅在阳光可以照到的一端部内表面安装反射膜。光学仿真模型中聚光器各部件的材料光学特征参数如表 1所示。
表 1
光学仿真模型中聚光器各部件的材料光学特征参数
| 部件 | 材料属性 | 光学特性 |
| 镜元 | 玻璃 | 反射率为0.9 |
| 外框 | 铝 | 反射率为0.1 |
| 吸热管 | 阳极氧化铝 | 吸收率为1.0 |
| 反射膜 | 玻璃 | 反射率为0.9 |
| 光源 | 平行光源 | 100万条光线 |
1.3.2 逐时光学效率与太阳方位角的函数关系
由于聚光器的光学效率是太阳高度角和太阳方位角的函数,因此通过数据拟合获得聚光器逐时光学效率ηh随太阳高度角α和太阳方位角γ变化的函数关系式。
首先,利用光学模拟获得呼和浩特、北京、上海、拉萨4地每月1日9时至15时的聚光器逐时光学效率,并提取相应工况下的方位角、高度角为拟合公式的数据集。
其次,利用数据拟合方式获得函数关系式为
| $ \eta_{\mathrm{h}}=z_0+z_1 \sin \alpha+z_2 \cos \alpha+z_3 \sin \gamma+z_4 \cos \gamma $ | (2) |
式中:z0,z1,z2,z3,z4——拟合系数。
其中,各拟合系数及相关系数R2的拟合参数值如表 2所示。
表 2
逐时光学效率拟合参数值
| 系数 | 太阳方位角跟踪 | 太阳高度角跟踪 | 系数 | 太阳方位角跟踪 | 太阳高度角跟踪 | |
| z0 | −0.088 | −0.320 | z3 | 0.074 | 0.009 | |
| z1 | 0.713 | 0.838 | z4 | −0.006 | 0.141 | |
| z2 | 0.155 | 0.287 | R2 | 0.993 | 0.997 |
最后,为检验该拟合函数的准确性,利用式(2)计算出上述4地在不同时间的逐时光学效率,并与光学模拟结果进行对比。
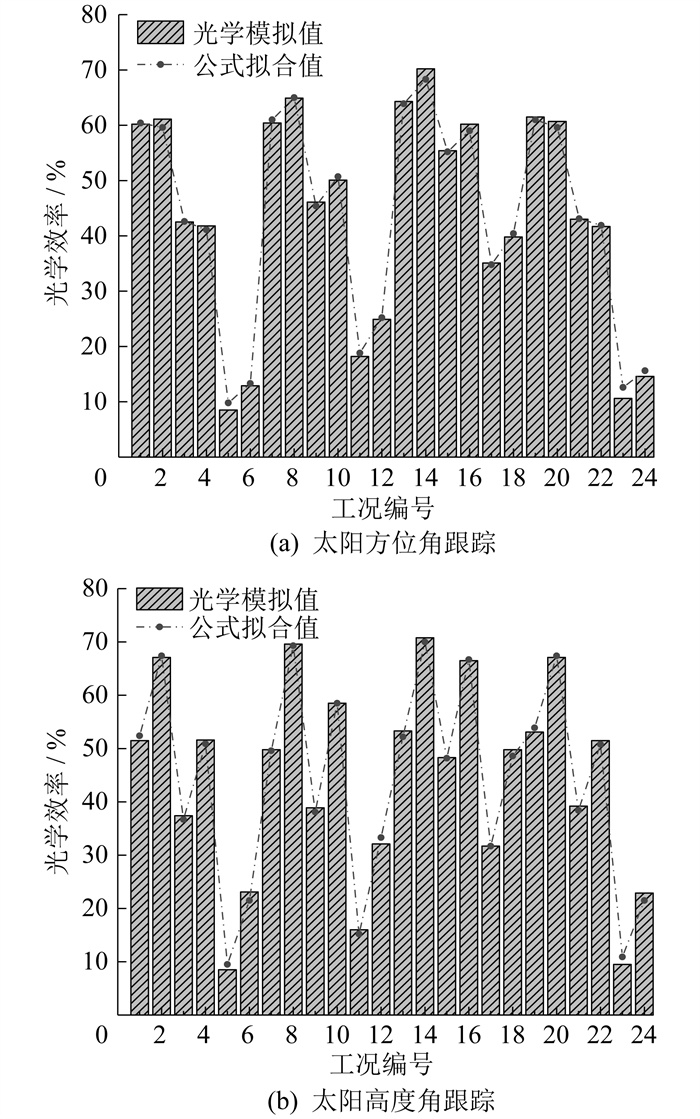
两种跟踪方式下逐时光学效率的光学模拟值与公式拟合值比较如图 3所示。其中,横坐标所示的工况编号1~24分别为上海、北京、呼和浩特、拉萨4个城市在冬至日、春分日、夏至日9时和12时的聚光器光学模拟。
由图 3可知,无论是太阳方位角跟踪还是太阳高度角跟踪,通过拟合公式计算的光学效率与光学模拟结果间的平均误差仅为0.8%,表明该回归公式能够较为准确地获得双焦点微型聚光器在4的地的全年逐时光学效率。
1.4 聚光器安装地逐时辐照度特征
计算加权平均光学效率还需从气象数据库中获得逐时辐照度。根据地理位置及气候类型,本文选择了呼和浩特、北京、拉萨、上海4个典型城市。在地理位置方面,每个城市都位于地区中心,人口数量大、建筑多,可利用的建筑立面太阳能资源丰富;在气候类型方面,4个城市覆盖了3种不同气候类型地区,即冰冻区、寒冷区、夏热冬冷区[13],不同气候类型对应不同的经纬度。4个城市的经纬度及相关信息如表 3所示。
表 3
4个城市的经纬度及相关信息
| 气候类型区 | 城市 | 纬度/°N | 经度/°E | 年平均气温/℃ | 日均总辐射量/(MJ/m2) |
| 冰冻区 | 呼和浩特 | 41.0 | 110 | 2~14 | 17.4 |
| 寒冷区 | 北京 | 40.0 | 116 | 9~19 | 13.5 |
| 寒冷区 | 拉萨 | 29.0 | 91 | 3~17 | 18.3 |
| 夏热冬冷区 | 上海 | 31.4 | 121 | 15~22 | 12.5 |
2 结果分析
2.1 端部反射膜对逐时光学效率的影响
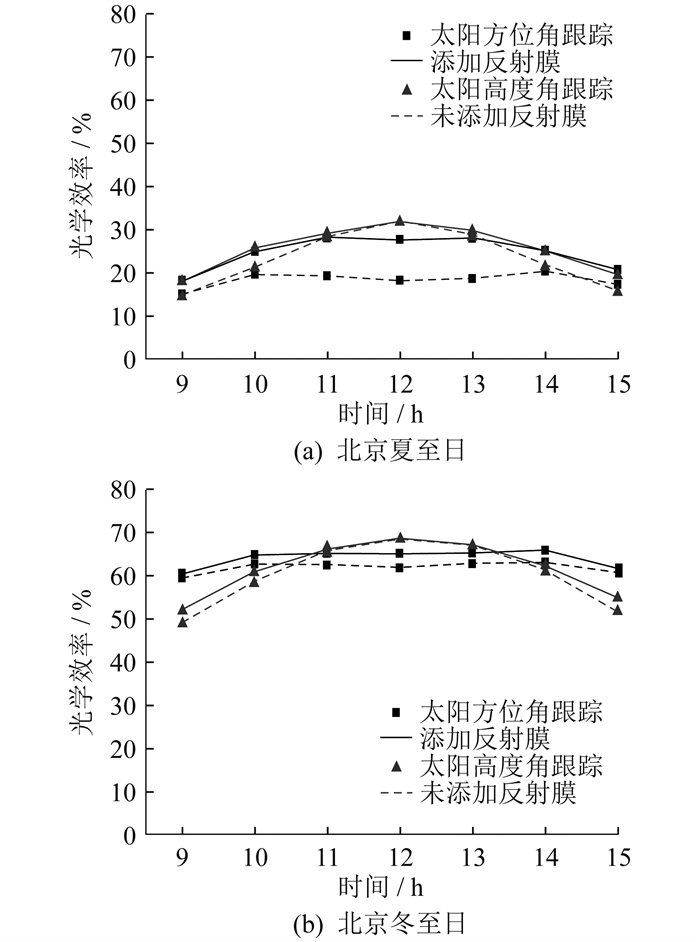
聚光器安装在北京建筑物外墙时,安装反射膜前后夏季与冬季逐时光学效率变化趋势如图 4所示。
由图 4可知,当聚光器安装在建筑外墙时,冬季逐时光学效率明显高于夏季,最高可达到70%,而夏季却只有30% 左右。在聚光器端部内表面添加反射膜后,太阳方位角跟踪的聚光器光学效率在夏季和冬季显著改善,分别提升了10% 和5%。此外,太阳高度角跟踪的光学效率也有一定程度的提升,在夏季和冬季分别增加了5%和3%。
由此可见,聚光器安装于建筑外墙时,无论采用哪种跟踪方式,均无法避免端部损失,从而降低了太阳能聚光器的光学效率。但是在太阳能聚光器的端部内侧安装反射膜,可以有效减少系统末端损失。安装反射膜前后的太阳能聚光器光路如图 5所示。
由图 5可知,反射膜将原本会偏离的部分光线二次反射回接收体,从而降低末端损失对光学效率的负面影响。
2.2 聚光器在不同城市不同安装方式下的加权平均光学效率
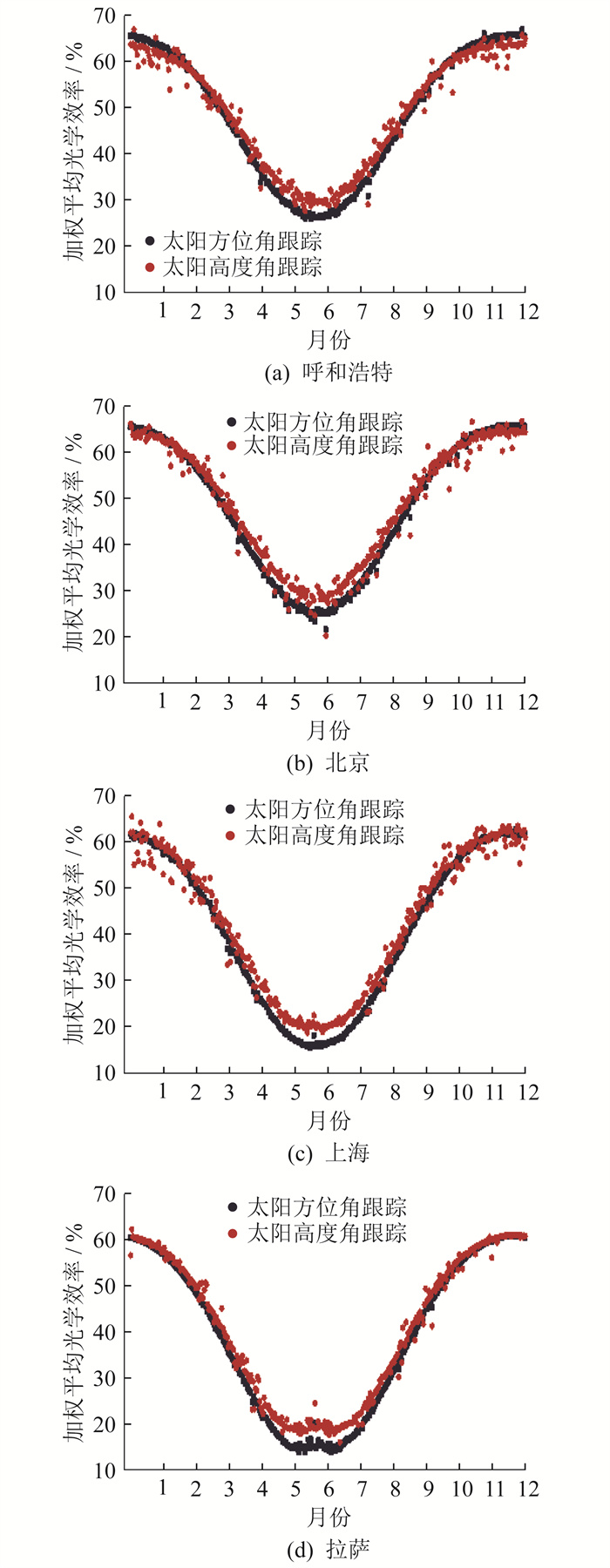
根据式(1)计算4个城市聚光器不同安装方式下的加权平均光学效率,具体如图 6所示。
由图 6可知,不同跟踪方式下的加权平均光学效率均随时间变化呈现出开口向上的二次曲线。在不同安装地点,夏季聚光器的加权平均光学效率均小于冬季。此外,呼和浩特全年加权平均光学效率在30%~65%,而上海则是在15%~ 60%。这是因为聚光器安装在建筑外墙时,相较于低纬度地区,高纬度地区的太阳辐照度在建筑立面上的数值更大,阳光与立面的夹角也更大,聚光器本身的光学损失较小、效率更高。
聚光器在纬度不同的上海(31.4°N,121°E)与呼和浩特(41.0°N,110°E)的加权平均光学效率不同,呼和浩特各月的加权平均光学效率更高,两者的差距在5%~10% 之间。对于纬度相近的上海(31.4°N,121°E)与拉萨(29.0°N,91°E),两地加权平均光学效率并未有明显的差距,全年效率在20%~60% 之间。这说明当聚光器安装于建筑立面时,安装地的经度基本不影响其性能变化,而纬度对其性能的影响较为显著。
综合全年计算结果并考虑秋季、冬季用热需求较大的建筑用能特点,可以发现:在较高纬度地区如北京和呼和浩特,秋季、冬季时太阳方位角跟踪下的聚光器性能更优,其加权平均光学效率可达到65%,而太阳高度角跟踪下的加权平均光学效率仅有61%;在中低纬度区如上海和拉萨,在秋季、冬季时,聚光器两种安装方式的加权平均光学效率差异较小,在夏季时,太阳方位角跟踪下的加权平均光学效率低于太阳高度角跟踪下的光学效率。因此,当采用这种聚光器作为集热方式时,在较高纬度地区的建筑外墙应采用太阳方位角跟踪。
3 结论
本文通过结合太阳辐射强度与聚光器光学效率两个因素,建立了加权平均光学效率的计算模型,并基于该模型分析了安装于建筑外墙的双焦点微型菲涅尔聚光器在不同地区、全年不同时段的光学性能,得出如下主要结论:
(1)端部安装反射膜可有效减少微型聚光器安装在建筑外墙时的末端光学损失;
(2)微型聚光器安装在建筑外墙时,不同地理位置下秋季、冬季的光学效率均高于夏季;
(3)综合全年计算结果以及秋季、冬季用热需求较大的建筑用能特点,当采用微型聚光器集热时,在较高纬度地区的建筑外墙应采用太阳方位角跟踪。
参考文献
-
[1]ELGHAMRY R, HASSAN H, HAWWASH A. A parametric study on the impact of integrating solar cell panel at building envelope on its power, energy consumption, comfort conditions and CO2 emissions[J]. Journal of Cleaner Production, 2020, 249: 119374. DOI:10.1016/j.jclepro.2019.119374
-
[2]MARSZAL A J, HEISELBERG P, BOURRELLA J S, et al. Zero energy building-a review of definitions and calculation methodologies[J]. Energy and Buildings, 2011, 43: 971-979. DOI:10.1016/j.enbuild.2010.12.022
-
[3]CHENG L, ZHANG F L, LI S Y, et al. Solar energy potential of urban buildings in 10 cities of China[J]. Energy, 2020, 196: 117038. DOI:10.1016/j.energy.2020.117038
-
[4]谢飞. 单轴菲涅尔反射聚光CPV/T系统的分析与研究[J]. 上海电力大学学报, 2022, 38(6): 605-609.
-
[5]吴俊, 安巍, 庞波, 等. 建筑整合式太阳能微型聚光器集热性能测试与分析[J]. 东北电力大学学报, 2022, 42(2): 26-32.
-
[6]方鑫, 何俊颖, 安巍. 建筑整合式双焦点微型聚光器的设计与性能分析[J]. 上海电力大学学报, 2023, 39(2): 203-209.
-
[7]DUAN Z X, AN W. Promote optical performance of linear Fresnel micro-concentrator by an offset-axis mirror layout in building-integrated PV/T application[J]. Renewable Energy, 2022, 200: 1047-1058. DOI:10.1016/j.renene.2022.10.057
-
[8]杜春旭, 王普, 吴玉庭, 等. 线性菲涅尔不同镜场光学性能比较[J]. 太阳能学报, 2013, 8(34): 1353-1359.
-
[9]门静婧, 赵雪茹, 冷亚坤, 等. 线性菲涅尔聚光集热系统光学综合性能的多目标优化研究[J]. 工程热物理学报, 2020, 41(7): 1706-1711.
-
[10]MARIA J M, CARLO R, RUBEN A, et al. A comparative analysis of configurations of linear Fresnel collectors for concentrating solar power[J]. Energy, 2014, 73: 192-203. DOI:10.1016/j.energy.2014.06.010
-
[11]宋固. 线性菲涅尔反射式太阳能集热系统研究[D]. 济南: 山东大学, 2011.
-
[12]SAEB M B, YOGI G. A computationally efficient method for the design of the heliostat field for solar power tower plant[J]. Renewable Energy, 2014, 69: 226-232. DOI:10.1016/j.renene.2014.03.043
-
[13]CHEN S Q, LI N P, YOSHINO H, et al. Statistical analyses on winter energy consumption characteristics of residential buildings in some cities of China[J]. Energy and Buildings, 2011, 43: 1063-1070. DOI:10.1016/j.enbuild.2010.09.022